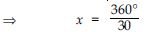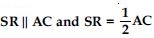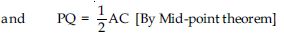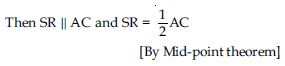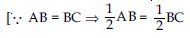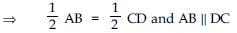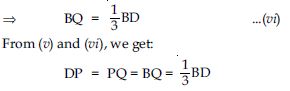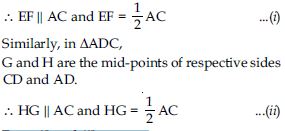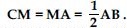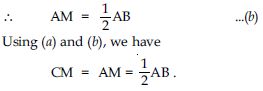Question 1:
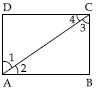
The angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all angles of the quadrilateral.
Answer:
The angles of a quadrilateral are in the ratio
3 : 5 : 9 : 13.
So, ∠A = 3x
∠B = 5x
∠C = 9x
∠D = 13x
where x is a positive constant.
Now, ∠A + ∠B + ∠C + ∠D = 360
[Angle sum property of a quadrilateral]
3x + 5x + 9x + 13x = 360
30x = 360
x = 12
Now,
∠A = 3x ∠A = 3 × 12 = 36
∠B = 5x ∠B = 5 × 12 = 60
∠C = 9x ∠C = 9 × 12 = 108
and ∠D = 13x ∠D = 13 × 12 = 156
Hence, angles of given quadrilateral are 36, 60, 108 and 156 respectively.
Question 2:
If the diagonals of a parallelogram are equal, show that it is a rectangle.
Answer:
Given: ABCD is a gm with diagonal AC
= diagonal BD
To prove: ABCD is a rectangle.
Proof: In s ABC and ABD, we have
AB = AB ... (Common side)
AC = BD (Given)
and AD = BC (Opp. sides of a II gm)
ABC BAD
(By SSS congruence rule)
∠DAB = ∠CBA ...(i)
(Property of congruency)
But ∠DAB + ∠CBA = 180 ...(ii)
[ AD II BC and AB cuts them, the sum of the
int. ∠s on the same side of transversal is 180.]
From (i) and (ii), we get:
∠DAB = ∠CBA = 90
Hence, ABCD is a rectangle.
[ If one angle of II gm is 90, it is a rectangle.]
[Hence Proved]
Question 3:
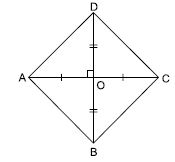
Show that if diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Answer:
Let ABCD be a rhombus.
Let its diagonal AC and BD bisect each other at right angle at point O.
OA = OC, OB = OD
and ∠AOB = ∠BOC = ∠COD
= ∠AOD = 90
We have to prove that ABCD is a rhombus.
In AOD and BOC,
OA = OC (Given)
∠AOD = ∠BOC (Each = 90) (Given)
OD = OB (Given)
AOD COB
(SAS criteria of congruency)
So, AD = CB ...(i)
(Corresponding parts of congruent triangles)
In AOB and COD,
OA = OC (Given)
∠AOB = ∠COD (Each = 90) (Given)
OB = OD (Given)
AOB COD
(SAS criteria of congruency)
So, AB = CD (Corresponding part of
congruent triangles) ...(ii)
Now in AOB and BOC,
AO = OC (Given)
∠AOB = ∠BOC
(each = 90) (Given)
OB = OB (Common)
AOB BOC
(SAS criteria of congruency)
So, AB = BC ...(iii)
(Corresponding parts of congruent triangles)
From (i), (ii) and (iii), we get
AD = BC = CD = AB
So, in addition to given conditions that the diagonals of a quadrilateral bisect each other
at right angle; we also have all its sides equal. Hence, quadrilateral satisfies all the
conditions to be a rhombus. Therefore given quadrilateral is a rhombus.
Question 4:
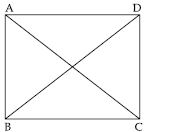
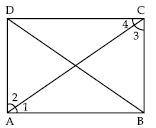
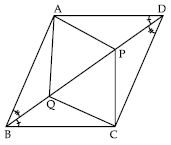
Show that the diagonals of a square are equal and bisect each other at right angles.
Answer:
Given: ABCD is a square. AC and BD are its diagonals bisect each other at point O.
To prove: (i) AC = BD, (ii) AC BD at point O.
<img height="218" src= "images/MBD_SR_METH_G9_img_300.jpg" width="360"> Proof: In s ABC and BAD,
AB = AB (Common side)
∠ABC = ∠BAD (Each 90)
BC = AD (Sides of a square)
ABC BAD [SAS congruence rule]
AC = BD (c.p.c.t.)
Hence, part (i) is proved.
In s AOB and AOD,
AO = AO (Common sides)
AB = AD (Sides of a square)
OB = OD
(Diagonals of a square bisect each other)
AOB AOD (SSS congruence rule)
∠AOB = ∠AOD (c.p.c.t.)
But ∠AOB + ∠AOD = 180 (Linear pair angles)
∠AOB = ∠AOD = 90
i.e. OA BD or AC BD.
Hence, part (ii) is proved.
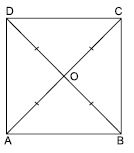
Question 5:
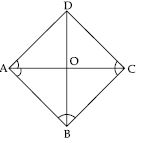
Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Answer:
Let ABCD be a quadrilateral in which equal diagonals AC and BD bisect each other at right
angle at point O.
We have
AC = BD
OA = OC ...(i)
and OB = OD ...(ii)
AC = BD
OA + OC = OB + OD
OC + OC = OB + OB [Using (i) and (ii)]
2OC = 2OB
OC = OB ...(iii)
From (i), (ii) and (iii), we get:
OA = OB = OC = OD ...(iv)
Now in AOB and COD,
OA = OD [Shown in part (iv)]
∠AOB = ∠COD
[Vertically opposite angles]
OB = OC [Shown in part (iv)]
AOB DOC
[SAS criteria of congruency]
So AB = DC (c.p.c.t) ...(v)
Similarly, BOC AOD
[SAS criteria of congruency]
So, BC = AD (c.p.c.t) ...(vi)
(v) and (vi) implies that opposite sides of
quadrilateral ABCD are equal.
Hence, ABCD is a parallelogram.
Now in ABC and BAD,
AB = BA [Common side]
BC = AD [Proved in part (vi)]
AC = BD (Given)
ABC BAD
[SSS criteria of congruency]
So, ∠ABC = ∠BAD (c.p.c.t) ...(vii)
But ∠ABC + ∠BAD = 180 ...(viii)
[ ABCD is a parallelogram (Proved above)]
AD || BC and AB as a transversal
∠ABC + ∠ABC = 180 [Using (vii) in (viii)]
2 ∠ABC = 180
∠ABC = 90
∠ABC = ∠BAD = 90 ...(ix)
Opposite angles of a parallelogram are equal
But ∠ABC = 90 and ∠BAD = 90
∠ABC = ∠ADC = 90 ...(x)
and ∠BAD = ∠BCD = 90 ...(xi)
We observe that
∠ABC = ∠ADC = ∠BAD
= ∠BCD = 90 ...(xii)
Now in AOB and BOC
OA = OC (given)
∠AOB = ∠BOC [each 90 (given)]
OB = OB (Common)
AOB COB
(SAS rule of congruency)
So, AB = BC ...(xiii)
From (v), (vi) and (xiii), we get:
AB = BC = CD = AD ...(xiv)
Using (xii) and (xiv);
Now we have the quadrilateral whose equal diagonals bisect each other at right angle.
Also sides are equal making an angle of 90 with each other.
Hence, given quadrilateral satisfy all conditions to be a square.
Question 6:
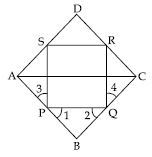
Diagonal AC of a parallelogram ABCD bisects ∠A (see fig.). Show that
(i) It bisects ∠C also
(ii) ABCD is a rhombus.
Answer:
It is given that diagonal AC bisects ∠A of the || gm ABCD.
To prove: AC bisects ∠C
Proof: Since AB DC and AC intersects them
∠1 = ∠3 (Alternate angles) ...(a)
Similarly, ∠2 = ∠4 ...(b)
But ∠1 = ∠2 ( AC bisects ∠A) ...(c)
∠3 = ∠4 [Using (a), (b) and (c)]
Thus, AC bisects ∠C.
Question 7:
ABCD is a rhombus. Show that the diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
Answer:
ABCD is a rhombus.
AB = BC = CD = AD
Let O be the point of bisection of diagonals.
OA = OC and OB = OD
In AOB and AOD,
OA = OA (Common)
AB = AD[Equal sides of rhombus]
OB = OD
[Diagonals of rhombus bisect each other]
AOB AOD
[SSS criteria of congruency]
So, ∠OAD = ∠OAB
(Corresponding parts of congruent triangles)
OA bisects ∠A ....(i)
Similarly, BOC DOC
(SSS criteria of congruency)
So; ∠OCB = ∠OCD [c.p.c.t]
OC bisects ∠C ...(ii)
From (i) and (ii), we can say that diagonal AC
bisects ∠A and ∠C.
Now in AOB and BOC,
OB = OB (Common)
AB = BC [Equal sides of rhombus]
OA = OC
[ Diagonals of rhombus bisect each other]
AOB COB
[SSS criteria of congruency]
So, ∠OBA = ∠OBC (c.p.c.t)
OB bisects ∠B ...(iii)
Similarly, AOD COD [SSS congruency]
∠ODA = ∠ODC (c.p.c.t.)
From (iii) and (iv) we can say that diagonal BD bisects ∠B and ∠D.
Question 8:
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
ABCD is a square
Answer:
ABCD is a rectangle
AB = DC ...(a)
and BC = AD
Also each angle; ∠A = ∠B = ∠C = ∠D = 90
In ABC and ADC,
∠1 = ∠2
and ∠3 = ∠4
[ AC bisects ∠A and ∠C (given)]
AC = AC (Common)
ABC ADC
(ASA criteria of congruency)
So, AB = AD ...(b)
From (a) and (b), we get:
AB = BC = AD = DC
It implies that all sides of a rectangle are
equal.
Hence, it is a square.
Question 9:
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
Diagonal BD bisects both ∠B as well as ∠D.
Answer:
ABCD is a rectangle
AB = DC ...(a)
and BC = AD
Also each angle; ∠A = ∠B = ∠C = ∠D = 90
In ABD and BDC
AB = BC [ Rectangle ABCD is a square proved in part (i)]
AD = DC
(proved in part (i) as ABCD is a square)
BD = BD (Common)
ABD CBD
(SSS criteria of congruency)
So, ∠ABD = ∠CBD (c.p.c.t.) ...(c)
and ∠ADB = ∠CDB (c.p.c.t.) ...(d)
(c) and (d) implies that diagonal BD bisects
both ∠B and ∠D.
Question 10:
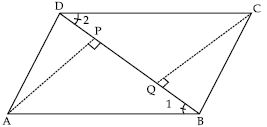
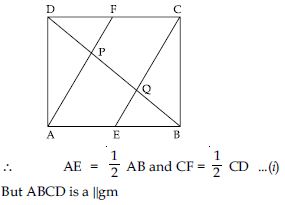
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see fig.). Show that
APD CQB
Answer:
In APD and CQB,
DP = BQ (given)
∠ADP = ∠QBC
[ In parallelogram ABCD,
AD BC; BD being a transversal.
∠ADB = ∠DBC (alternate angles)
So;∠ADP = ∠QBC]
AD = CB [ Opposite sides of parallelogram are equal]
APD CQB (SAS criteria of congruency)
Question 11:
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see fig.). Show that
AP = CQ
Answer:
So; AP = CQ (Corresponding parts of congruent triangles)
Question 12:
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see fig.). Show that
AQB CPD
Answer:
In AQB and CPD,
BQ = DP (Given)
∠ABQ = ∠PDC
[ In parallelogram ABCD,
AB || CD; BD being a transversal.
∠ABD = ∠BDC (Alternate angles)
So;∠ABQ = ∠PDC]
AB = CD [Opposite sides of a parallelogram are equal]
AQB CPD
[SAS criteria of congruency]
Question 13:
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see fig.). Show that
AQ = CP
Answer:
So, AQ = CP (Corresponding parts of congruent triangles)
Question 14:
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see fig.). Show that
APCQ is a parallelogram
Answer:
In quadrilateral APCQ; we have
AP = CQ [Proved in part (ii)]
AQ = CP [Proved in part (iv)]
Opposite sides of quadrilateral APCQ are equal.
As we know that in a parallelogram opposite sides are equal.
Hence, APCQ is a parallelogram.
Question 15:
ABCD is a parallelogram and AP and CQ are the perpendiculars from vertices A and C on its
diagonal BD (see fig.).
Show that:
APB CQD
Answer:
ABCD is a parallelogram
AB DC
BD being a transversal.
So, ∠1 = ∠2 (Alternate angles)
Now in APB and CQD,
∠APB = ∠CQD (each = 90) (Given)
∠1 = ∠2 (Proved above)
AB = CD [Opposite sides of a
parallelogram are equal]
APB CQD
(AAS criteria of congruency)
Question 16:
ABCD is a parallelogram and AP and CQ are the perpendiculars from vertices A and C on its
diagonal BD (see fig.).
Show that:
AP = CQ
Answer:
ABCD is a parallelogram
AB DC
BD being a transversal.
So, ∠1 = ∠2 (Alternate angles)
So, AP = CQ [Corresponding parts of congruent triangles]
Question 17:
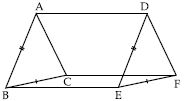
In ABC and DEF; AB = DE, AB II DE, BC = EF and BC II EF. Vertices A, B and C are joined to
vertices D, E and F respectively (see fig.).
Show that
Quadrilateral ABED is a parallelogram
Answer:
Given: In ABC and DEF,
AB = DE and AB II DE
Also in s, BC = EF and BC II EF
In quad. ABED, its one pair of opposite sides AB and DE are such that AB = DE and AB II
DE
ABED is a II gm.
AD = BE and AD II BE.
[Opp. sides of a gm are equal and parallel] ... (i)
Question 18:
In ABC and DEF; AB = DE, AB II DE, BC = EF and BC II EF. Vertices A, B and C are joined to
vertices D, E and F respectively (see fig.).
Show that
Quadrilateral BEFC is a parallelogram
Answer:
Given: In ABC and DEF,
AB = DE and AB II DE
Also in s, BC = EF and BC II EF
Again, quad. BEFC
BE = CF and BE CF
BEFC is a gm.
Question 19:
In ABC and DEF; AB = DE, AB DE, BC = EF and BC EF. Vertices A, B and C are joined to vertices D,
E and F respectively (see fig.).
Show that
AD II CF and AD = CF
Answer:
Given: In ABC and DEF,
AB = DE and AB II DE
Also in s, BC = EF and BC EF
CF = BE and CF II BE ... (ii)
From (1) and (2), we get
AD = CF and AD II CF
Question 20:
In ABC and DEF; AB = DE, AB II DE, BC = EF and BC II EF. Vertices A, B and C are joined to
vertices D, E and F respectively (see fig.).
Show that
Quadrilateral ACFD is a parallelogram
Answer:
Given: In ABC and DEF,
AB = DE and AB II DE
Also in s, BC = EF and BC II EF
ACFD is a IIgm. [If one pair of opp. sides
of quad. is equal and parallel, it is a IIgm.]
Question 21:
In ABC and DEF; AB = DE, AB II DE, BC = EF and BC II EF. Vertices A, B and C are joined to
vertices D, E and F respectively (see fig.).
Show that
AC = DF
Answer:
Given: In ABC and DEF,
AB = DE and AB II DE
Also in s, BC = EF and BC II EF
Hence, AC = DF [Opp. sides of a gm]
Question 22:
In ABC and DEF; AB = DE, AB II DE, BC = EF and BC II EF. Vertices A, B and C are joined to vertices D, E and F respectively (see fig.).
Show thatABC DEF
Answer:
Given: In ABC and DEF,
AB = DE and AB II DE
Also in s, BC = EF and BC II EF
In ABC and DEF,
AB = DE (Given)
BC = EF (Given)
AC = DF [Proved in part (v)]
ABC DEF
(SSS criteria of congruency)
Question 23:
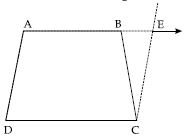
ABCD is a trapezium in which AB II CD and AD = BC (See fig.)
Show that:
∠A = ∠B
Answer:
Extend AB and draw a line CE parallel to AD as shown in the figure.
Since, AD II CE and transversal AE cuts them at A and E respectively.
∠A + ∠E = 180
∠A = 180 – ∠E ...(i)
Since AB II CD and AD II CE
AECD is a IIgm
AD = CE
BC = CE [AD = BC (Given)]
Thus, in BCE, we have
BC = CE
∠CBE = ∠CEB
[Equal angles opp. to equal sides]
180 – ∠B = ∠E
[ ∠CBE + ∠ABC = 180 (Linear pair)
∠CBE = 180 – ∠ABC]
180 – ∠E = ∠B ...(ii)
From (i) and (ii), we get ∠A = ∠B
Question 24:
ABCD is a trapezium in which AB CD and AD = BC (See fig.)
Show that:
∠C = ∠D
Answer:
ABCD is a trapezium in which AB || DC
∠A + ∠D = 180 ...(a)
and ∠B + ∠C = 180 ...(b)
[For two parallel lines sum of interior angles on the same side of a transversal is
180.]
Equating (a) and (b), we get:
∠A + ∠D = ∠B + ∠C
But ∠A = ∠B proved in part (i)
∠A + ∠D = ∠A + ∠C
∠D = ∠C
or ∠C = ∠D [Hence proved]
Question 25:
ABCD is a trapezium in which AB CD and AD = BC (See fig.)
Show that:
ABC BAD
Answer:
In ABC and BAD,
AB = AB, (Common)
∠A = ∠B [Proved in part (i)]
BC = AD (given)
ABC BAD
(SAS criteria of congruency)
Question 26:
ABCD is a trapezium in which AB CD and AD = BC (See fig.)
Show that:
diagonal AC = diagonal BD.
Answer:
So, AC = BD (Corresponding part of congruent triangles)
i.e., in trapezium ABCD;
diagonal AC = diagonal BD.
Question 27:
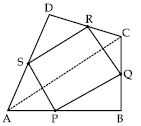
ABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively (see fig.)
AC is a diagonal.
Show that
Answer:
In ABC,
P is the mid-point of AB and Q is the mid-point of BC.
Then PQ II AC
In ACD,
R is the mid-point of CD and S is the
mid-point of AD.
Question 28:
ABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively (see fig.)
AC is a diagonal.
Show that
PQ = SR
Answer:
In ABC,
P is the mid-point of AB and Q is the mid-point of BC.
Then PQ AC
Question 29:
ABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively (see fig.)
AC is a diagonal.
Show that
PQRS is a parallelogram.
Answer:
In ABC,
P is the mid-point of AB and Q is the mid-point of BC.
Then PQ II AC
PQ II AC
and SR II AC
PQ II SR [ Two lines parallel
to a given line are parallel to each other.]
Now, we have
PQ = SR
and PQ II SR
As we know that if one pair of opposite sides of a quadrilateral is equal and parallel then it is a parallelogram.
PQRS is a parallelogram.
Question 30:
ABCD is a rhombus and P, Q, R, S are the mid-points of AB, BC, CD and DA respectively. Prove that quadrilateral PQRS is a rectangle.
Answer:
Given: P, Q, R and S are the mid-points of respective sides AB, BC, CD and DA of rhombus.
PQ, QR, RS and SP are joined.
To prove: PQRS is a rectangle.
Construction: Join A and C.
Proof: In ABC, P is the mid-point of AB and Q is the mid-point of BC.
By mid-point theorem,
Now in s APS and CQR, we have AP = CQ
AP = CQ where P and Q are midpoints
of AB and BC.]
Similarly, AS = CR
PS = QR
[Opposite sides of gm PQRS]
APS CQR
[By SSS Congruence rule]
∠3 = ∠4 (c.p.c.t.)
Now we have
∠1 + ∠SPQ + ∠3 = 180
and ∠2 + ∠PQR + ∠4 = 180 [Linear pairs]
∠1 + ∠SPQ + ∠3 = ∠2 + ∠PQR + ∠4
Since ∠1 = ∠2 and ∠3 = ∠4
(As proved above)
∠SPQ = ∠PQR ... (iii)
Now, PQRS is a gm (as proved above)
∠SPQ + ∠PQR = 180 ... (iv)
[ SP RQ and PQ cuts them and the sum
of int. ∠s on the same side of a transversal is
180.]
Using (iii) in (iv) we get:
∠SPQ + ∠SPQ = 180
2∠SPQ = 180
∠SPQ = 90
Thus, PQRS is a gm whose one angle
∠SPQ = 90.
Hence, PQRS is a rectangle.
Question 31:
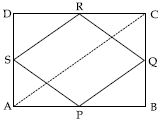
ABCD is a rectangle and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Answer:
Given: A rectangle ABCD in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively PQ, QR, RS and SP are joined.
To prove: PQRS is a rhombus
Construction: Join AC
Proof: In ABC, P and Q are the mid-points of sides AB, BC respectively.
AS = BQ ... (iv)
In s APS and BPQ, we have:
AP = BP
[ P is the mid-point of AB.]
∠PAS = ∠PBQ [Each is 90]
and AS = BQ [From (iv)]
APS BPQ
[SAS criterion of congruency]
PS = PQ ... (v)
[Corresponding parts of congruent triangles are equal]
From (iii) and (v), we get PQRS is a
parallelogram such that
PS = PQ
i.e., two adjacent sides are equal.
Hence, PQRS is a rhombus.
Question 32:
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see fig.). Show that the line segments AF and EC trisect the diagonal BD.
Answer:
Since E and F are the mid-points of AB and CD respectively.
AE = FC and AE II FC [From (i)]
AECF is a IIgm
FA II CE
FP II CQ ...(ii)
[ FP is a part of FA and CQ is a part of CE]
We know that, the segment drawn through the mid-point of one side of a triangle and parallel
to the other side bisects the third side.
In DCQ, F is the mid-point of CD and
FP II CQ [From (ii)]
P is the mid-point of DQ
DP = PQ ...(iii)
Similarly, in ABP, E is the mid-point of AB
and EQ II AP
Q is the mid-point of BP
BQ = PQ ...(iv)
From (iii) and (iv), we have
DP = PQ = BQ ...(v)
Now BD = BQ + PQ + DP
= BQ + BQ + BQ
BD = 3BQ
or 3BQ = BD
It implies that points P and Q trisects BD.
So, AF and CE trisects BD.
Question 33:
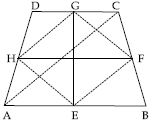
Show that the line segments joining the midpoints of opposite sides of a quadrilateral bisect each other.
Answer:
A quadrilateral ABCD in which EG and FH are the line-segments joining the mid-points of opposite sides of a quadrilateral.
To Prove: EG and FH bisect each other.
Construction: Join AC, EF, FG, GH and HE
Proof: In ABC, E and F are the mid-points of respective sides AB and BC.
From (i) and (ii), we get:
EF HG and EF = HG
EFGH is a parallelogram.
[ A quadrilateral is a parallelogram if one pair of its opposite sides is equal and
parallel.]
As we know, that the diagonals of a parallelogram bisect each other, therefore line segments
(i.e. diagonals) EG and FH (of parallelogram EFGH) bisect each other.
Question 34:
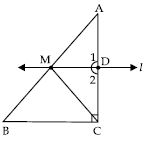
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and
parallel to BC intersects AC at D.
Show that:
D is the mid-point of AC
Answer:
Question 35:
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and
parallel to BC intersects AC at D.
Show that:
MD AC
Answer:
l II BC (Given)
Consider AC as a transversal
∠1 = ∠C(Corresponding angles)
∠1 = 90 [ ∠C = 90 (Given)]
Thus, MD AC.
Question 36:
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and
parallel to BC intersects AC at D.
Show that:
Answer:
In AMD and CMD,
AD = DC (Proved above)
∠1 = ∠2 (Each = 90)
[Proved above]
MD = MD (Common)
AMD CMD
(SAS criteria of congruency)
So, AM = CM ...(a) (c.p.c.t.)
Given that M is the mid-point of AB.