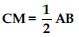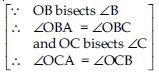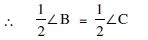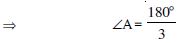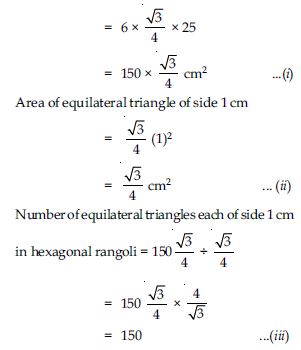Question 1:
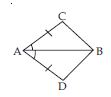
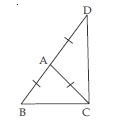
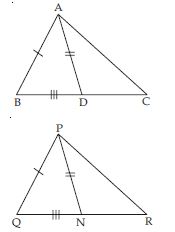
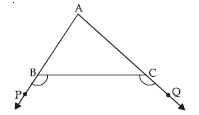
In quadrilateral ACBD, AC = AD and AB bisects ∠A (see fig.). Show that ABC ABD.
What can you say about BC and BD?
Answer:
Given that, in quadrilateral ACBD;
AC = AD and AB bisects ∠A.
We have to prove that ABC ABD.
Proof: In ABC and ABD,
AC = AD (given)
∠BAC = ∠BAD [ AB bisects ∠A (given)]
AB = AB (common)
ABC ABD [SAS criteria of congruency]
Thus BC = BD
(Congruent parts of congruent triangles)
Question 2:
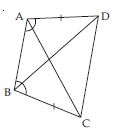
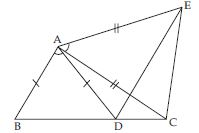
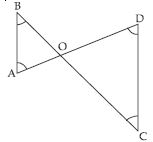
ABCD is a quadrilateral in which AD = BC
and ∠DAB = ∠CBA (see fig.). Prove that
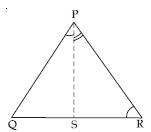
(i ) ABD BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.
Answer:
In ABD and ABC,
AD = BC (given)
∠DAB = ∠CBA (given)
AB = AB (common)
(i ) ABD BAC
(SAS criteria of congruency)
(ii) BD = AC
(Congruent parts of congruent triangles)
(iii) ∠ABD = ∠BAC
(Congruent parts of congruent triangles)
Question 3:
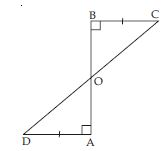
AD and BC are equal perpendiculars to a line segment AB (see fig.). Show that CD bisects AB.
Answer:
In BOC and AOD,
∠OBC = ∠OAD
[each 90 (given)]
∠BOC = ∠AOD
(vertically opposite angles)
BC = AD (given)
BOC AOD
(AAS criteria of congruency)
OB = OA
and OC = OD
(Congruent parts of congruent triangles)
It implies that O is the mid-point of line-segment
AB and CD.
Question 4:
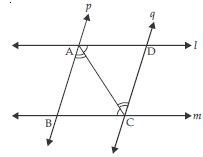
l and m are two parallel lines intersected by another pair of parallel lines p and q (see fig.) Show that ABC CDA.
Answer:
Given than l || m
AC being a transversal.
Therefore ∠ACB = ∠DAC (alternate angles)
p || q (given)
AC being a transversal.
Therefore∠BAC = ∠ACD (alternate angles)
Now in ABC and CDA,
∠ACB = ∠DAC (Proved above)
∠BAC = ∠ACD (Proved above)
AC = AC (Common)
ABC CDA
(AAS criteria of congruency)
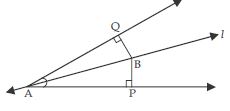
Question 5:
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars
from B to the arms of ∠A (see fig.). Show that:
(i) APB AQB
(ii) BP = BQ or B is equidistant from the
arms of ∠A.
Answer:
Given that line l bisects ∠A.
∠BAP = ∠BAQ
Now in APB and AQB,
∠BAP = ∠BAQ (given)
∠BPA = ∠BQA [each 90 (given)]
AB = AB (common)
APB AQB
(AAS criteria of congruency)
BP = BQ
Congruent parts of congruent triangles i.e., B is
equidistant from the arms of ∠A.
Question 6:
In fig., AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
Answer:
Given that
∠BAD = ∠EAC
Adding ∠DAC on both sides, we get
∠BAD + ∠DAC = ∠EAC + ∠DAC
∠BAC = ∠EAD ... (i)
Now in ABC and AED,
AB = AD (given)
AC = AE (given)
∠BAC = ∠EAD [From (i)]
ABC AED
(AAS criteria of congruency)
BC = DE
(Congruent parts of Congruent triangles)
Question 7:
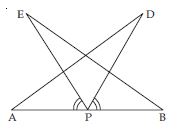
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such
that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see fig.). Show that
(i) DAP EBP
(ii) AD = BE
Answer:
Given that
∠EPA = ∠DPB
Adding ∠EPD on both sides, we get:
∠EPA + ∠EPD = ∠DPB + ∠EPD
∠APD = ∠BPE ... (i)
Now in DPA and EBP,
∠PAD = ∠PBE [ ∠BAD = ∠ABE
(given) ∠PAD = ∠PBE]
∠APD = ∠BPE [From (i)]
AP = PB
[ P is the mid-point of AB (given)]
DPA EBP
[AAS criteria of congruency]
AD = BE
(Congruent parts of congruent triangles)
Question 8:
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see fig.). Show that:
AMC BMD
Answer:
In AMC and BMD,
AM = BM
[ M is the mid-point of hyp. AB (given)]
∠AMC = ∠BMD
(vertically opp. angles)
CM = DM (given)
AMC BMD
(SAS criteria of congruency)
∠ACM = ∠BDM ... (a)
∠CAM = ∠DBM
and AC = BD (Congruent parts of
Congruent triangles)
Question 9:
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see fig.). Show that:
∠DBC is a right angle.
Answer:
For two lines AC and DB and transversal DC,
we have
∠ACD = ∠BDC (alternate angles)
[ ∠ACM = ∠BDM using (a)
∠ACD = ∠BDC]
AC || DB [ If alternate angles are equal then lines are parallel]
Now for parallel lines AC and DB and for transversal BC.
∠DBC = ∠ACB (alternate angles)
... (b)
But ABC is a rt. ∠d triangle, right angled at C.
∠ACB = 90 ... (c)
Therefore ∠DBC = 90 [Using (b) and (c)]
It implies that ∠DBC is a right triangle.
Question 10:
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see fig.). Show that:
DBC ACB
Answer:
Now in DBC and ACB,
DB = AC [Proved in part (i)]
∠DBC = ∠ACB
[each 90 proved in part (ii)]
BC = BC (common)
DBC ACB
(SAS criteria of congruency)
Question 11:
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see fig.). Show that:
Answer:
In part (iii) we have proved that
DBC ACB
DC = AB
DM + CM = AB
CM + CM = AB [ DM = CM (given)]
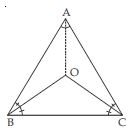
2 CM = AB
Question 12:
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other
at O. Join A to O show that:
OB = OC
Answer:
ABC is an isosceles triangle in which AB = AC
∠C = ∠B
(angles opposite to equal sides)
∠OCA + ∠OCB = ∠OBA + ∠OBC
∠OCB + ∠OCB = ∠OBC + ∠OBC
2∠OCB = 2∠OBC
∠OCB = ∠OBC
Now in OBC,
∠OCB = ∠OBC (proved above)
OB = OC (sides opposite to equal angles)
Question 13:
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other
at O. Join A to O show that:
AO bisects ∠A.
Answer:
Now in AOB and AOC
AB = AC (given)
∠OBA = ∠OCA
∠B = ∠C
BO bisects ∠B and CO bisects ∠C.
∠OBA = ∠OCA
AO = AO (Common)
AOB AOC
(SAS criteria of congruency)
∠OAB = ∠OAC
(Congruent parts of congruent triangles)
Hence AO; bisects ∠A.
Question 14:
In ABC, AD is the perpendicular bisector of BC (see fig.). Show that ABC is an isosceles triangle in which AB = AC.
Answer:
In ABD and ACD,
BD = CD
( AD bisects BC) [given]
∠ADB = ∠ADC
= each 90 ( AD BC) [given]
AD = AD [Common]
ABD ACD
(SAS criteria of congruency)
AB = AC
(Congruent parts of congruent triangles)
Therefore ABC is an isosceles triangle.
Question 15:
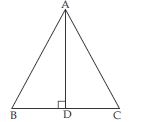
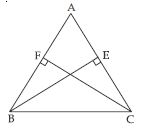
ABC is an isosceles triangle in which altitudes BE and CF are drawn to sides AC and AB respectively (see fig.). Show that these altitudes are equal.
Answer:
In ABE and ACF,
∠A = ∠A [Common]
∠AEB = ∠AFC (each = 90) [given]
AB = AC [given]
ABE ACF
(AAS criteria of congruency)
Therefore
BE = CF
(Congruent parts of congruent triangles)
In other words, altitudes drawn to respective equal sides are equal.
Question 16:
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see fig.). Show
that
(i) ABE ACF
(ii) AB = AC i.e., ABC is an isosceles triangle.
Answer:
In ABE and ACF,
∠A = ∠A (Common)
∠AEB = ∠AEC (each = 90)
[ BE AC and CF AB (given)]
BE = CF (given)
(i) ABE ACF
[AAS criteria of congruency]
(ii) So, AB = AC
[Congruent parts of congruent triangles]
i.e., ABC is an isosceles triangle.
Question 17:
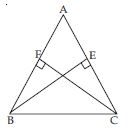
ABC and DBC are two isosceles triangles on the same base BC (see fig.). Show that ∠ABD = ∠ACD.
Answer:
In isosceles ABC,
AB = AC (given)
∠ACB = ∠ABC ... (i)
(angles opposite to equal sides)
Also in isosceles BCD,
BD = DC
∠BCD = ∠CBD ... (ii)
(angles opposite to equal sides)
Adding corresponding sides of (i) and (ii),
∠ACB + ∠BCD = ∠ABC + ∠CBD
∠ACD = ∠ABD
or ∠ABD = ∠ACD [Hence Proved]
Question 18:
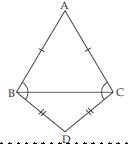
ABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see fig.). Show that ∠BCD is a right angle.
Answer:
In an isosceles triangle ABC;
AB = AC
∠ACB = ∠ABC ... (i)
(angles opposite to equal sides)
Now AD = AB (By construction)
But AB = AC (given)
AD = AB = AC
AD = AC
Now in ADC,
AD = AC
∠ADC = ∠ACD ... (ii)
[angles opposite to equal sides of ADC]
From Fig., we have
∠BAC + ∠CAD = 180 ... (iii)
(linear pair)
As we know that exterior angle of a triangle is equal to the sum of its interior opposite
angles.
In ABC,
∠CAD = ∠ABC + ∠ACB
= ∠ACB + ∠ACB [Using (i)]
∠CAD = 2∠ACB ... (iv)
Similarly for ADC;
∠BAC = ∠ACD + ∠ADC
[Same reason as above]
= ∠ACD + ∠ACD[Using (ii)]
∠BAC = 2∠ACD ... (v)
From (iii), (iv) and (v), we get:
2∠ACB + 2∠ACD=180
or 2(∠ACB + ∠ACD)=180
Question 19:
ABC is a right angled triangle in which ∠A = 90 and AB = AC. Find ∠B and ∠C.
Answer:
ABC is a right triangle in which
∠A = 90
and AB = AC
AB = AC
∠C = ∠B ... (i)
(angles opposite to equal sides)
Now in ABC,
∠A + ∠B + ∠C = 180
(angles sum property)
90 + ∠B + ∠B = 180
[ ∠A = 90 (Given) and ∠B = ∠C (from (i)]
2∠B = 180 – 90
2∠B = 90
∠B = 45
Also ∠C = ∠B
∠C = 45
Question 20:
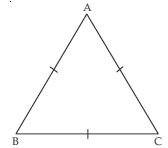
Show that the angles of an equilateral triangle are 60 each.
Answer:
Let ABC be an equilateral triangle
AB = BC
∠C = ∠A .. (i)
(angles opp. to equal sides)
Similarly
AB = AC
∠C = ∠B ... (ii)
(angles opp. to equal sides)
From (i) and (ii), we get
∠A = ∠B = ∠C ... (iii)
Now in ABC;
∠A + ∠B + ∠C= 180 ... (iv)
[angles sum property]
∠A + ∠A + ∠A=180
3∠A=180º
∠A=60
From (iii); ∠A = ∠B = ∠C
∠A = ∠B = ∠C = 60
Hence each angle of an equilateral triangle is 60.
Question 21:
ABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see fig.). If AD is extended to intersect BC at P, show that
ABD ACD
Answer:
ABC is an isosceles triangle.
AB = AC
DBC is also an isosceles triangle.
BD = CD
Now in ABD and ACD
AB = AC (given)
BD = CD (given)
AD = AD (common)
ABD ACD
(SSS criteria of congruency)
Proved part (i)
∠BAD = ∠CAD ... (a)
[Congruent parts of congruent triangles]
Question 22:
ABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see fig.). If AD is extended to intersect BC at P, show that
ABP ACP
Answer:
ABC is an isosceles triangle.
AB = AC
DBC is also an isosceles triangle.
BD = CD
Now in ABD and ACD
AB = AC (given)
BD = CD (given)
AD = AD (common)
Now in ABP and ACP
AB = AC (given)
∠BAD = ∠CAD [Using (a)]
AP = AP (common)
ABP ACP
(SAS criteria of congruency)
Question 23:
ABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see fig.). If AD is extended to intersect BC at P, show that
AP bisects ∠A as well as ∠D.
Answer:
ABC is an isosceles triangle.
AB = AC
DBC is also an isosceles triangle.
BD = CD
Now in ABD and ACD
AB = AC (given)
BD = CD (given)
AD = AD (common)
In part (ii), we have proved that
ABP ACP
So, ∠BAP = ∠CAP
(Congruent parts of congruent triangles)
It implies that AP bisects ∠A.
In part (i) we have proved that
ABD ACD
So, ∠ADB = ∠ADC ...(b)
(Congruent parts of congruent triangles)
∠ADB + ∠BDP = 180
(linear pair) ... (c)
∠ADC + ∠CDP = 180 ... (d)
(linear pair)
From (c) and (d), we get:
∠ADB + ∠BDP = ∠ADC + ∠CDP
or ∠ADB + ∠BDP = ∠ADB + ∠CDP
[Using (b)]
∠BDP = ∠CDP
DP bisects ∠D.
or we can say that AP bisects ∠D.
Question 24:
ABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see fig.). If AD is extended to intersect BC at P, show that
AP is the perpendicular bisector of BC.
Answer:
ABC is an isosceles triangle.
AB = AC
DBC is also an isosceles triangle.
BD = CD
Now in ABD and ACD
AB = AC (given)
BD = CD (given)
AD = AD (common)
In part (ii) we have proved that
ABP ACP
BP = PC ...(e)
(Congruent parts of congruent triangles)
and ∠APB = ∠APC (c.p.c.t.) ... (f)
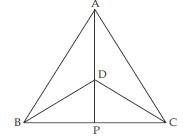
Now ∠APB + ∠APC = 180 (linear pair)
∠APB + ∠APB = 180 [Using (f)]
2∠APB = 180
∠APB = 90
AP BC ... (g)
From (e) we have BP = PC and from (g), we have
proved AP BC. So, collectively we can say that
AP is perpendicular bisector of BC.
Question 25:
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects ∠A.
Answer:
In ABD and ACD,
AB = AC (given)
∠ADB = ∠ADC (each = 90)
[ AD BC (given)]
AD = AD (common)
ABD ACD
(RHS rule of congruency)
So, BD = DC
(Congruent parts of congruent triangles)
It implies AD; bisects BC. (Proved part (i))
Also ∠BAD = ∠CAD
(Congruent parts of congruent triangles)
It implies AD bisects ∠A.
Question 26:
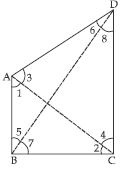
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of PQR (see fig). Show that:
ABM PQN
Answer:
Now in ABM and PQN,
AB = PQ (given)
AM = PN (given)
BM = QN [proved in part (c)]
ABM PQN
(SSS criteria of congruency)
So, ∠B = ∠Q ... (d)
(Congruent parts of congruent triangles)
Question 27:
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of PQR (see fig). Show that:
ABC PQR
Answer:
In ABC and PQR,
AB = PQ (given)
∠B = ∠Q [Using part (d)]
BC = QR (given)
ABC PQR
(SAS criteria of congruency)
Question 28:
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Answer:
In BEC and CFB,
∠BEC = ∠CFB (each = 90)
[ BE AC and CF AB]
BC = BC (common)
BE = CF (given)
BEC CFB
(RHS rule of congruency)
So, EC = FB ...(i)
(Congruent parts of congruent triangles)
Now, in AEB and AFC,
∠A = ∠A (common)
∠AEB = ∠AFC
(each = 90) [given]
EB = FC (given)
AEB AFC
(AAS criteria of congruency)
So, AE = AF ...(ii)
(Congruent parts of congruent triangles)
Adding (i) and (ii), we get:
EC + AE= FB + AF
AC = AB
Now, in ABC; we have
AB = AC
It implies that ABC is isosceles.
Question 29:
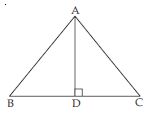
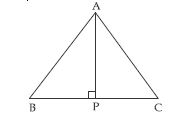
ABC is an isosceles triangle with AB = AC. Draw AP BC and show that ∠B = ∠C.
Answer:
Given: ABC is an isosceles triangle in which
AB=AC
To prove: ∠B=∠C
Construction: Draw AP BC.
Proof: In ABP and ACP,
∠APB=∠APC
(each = 90) [By construction]
AB =AC (given)
AP=AP (common)
ABP ACP
(RHS rule of congruency)
So, ∠B=∠C
(Congruent parts of congruent triangles)
Question 30:
Show that in a right angled triangle, the hypotenuse is the longest side.
Answer:
Let ABC be a right angled triangle, rt. angle at B. We have to prove that AC, the hypotenuse is the longest side.
In rt. ABC;
∠A + ∠B + ∠C= 180
∠A + 90+ ∠C = 180 [Since, ∠B = 90]
∠A + ∠C= 180 – 90 = 90
Now ∠A + ∠C= 90
and ∠B= 90
∠B >∠C and ∠B > ∠A
As we know that the greater angle has a longer
side opposite to it.
AC > AB and AC > BC.
In other words, ∠B being the greatest angle has the longest opposite side AC i.e.,
hypotenuse.
Question 31:
In fig., sides AB and AC of ABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC> AB.
Answer:
∠ABC + ∠PBC = 108 ...(i)
(linear pair axiom)
∠ACB + ∠QCB = 180 ...(ii)
(linear pair axiom)
From (i) and (ii), we get:
∠ABC + ∠PBC = ∠ACB + ∠QCB ...(iii)
But ∠PBC, ∠QCB (given) ...(iv)
Using (iv) in (iii), we have
∠ABC > ∠ACB
Now in ABC
∠ABC > ∠ACB
[Proved above in (iv)]
AC > AB
[Since, Side opposite to greater angle is longer.]
Question 32:
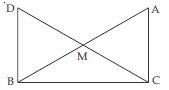
In fig., ∠B < ∠A and ∠C < ∠D. Show that AD < BC.
Answer:
In AOB;
∠B < ∠A (given)
or ∠A > ∠B
So; OB > OA ...(i)
[Since, Side opposite to greater angle is longer]
In COD;
∠C < ∠D (given)
or ∠D > ∠C
OC > OD ...(ii)
[Since, Side opposite to greater angle is longer]
Adding (i) and (ii), we get:
OB + OC > OA + OD
BC > AD
or AD < BC [Hence Proved]
Question 33:
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see fig., ). Show that ∠A >∠C and ∠B > ∠D.
Answer:
Given: ABCD is a quadrilateral. AB is the shortest side and CD is the longest side.
To prove: ∠A > ∠C and ∠B > ∠D.
Construction: Join A and C also B and D.
Proof: In ABC, AB is the smallest side
BC > AB
∠1 > ∠2 ...(i)
[Since, Angle opposite to longer side is greater]
In ADC, CD is the largest side
CD > AD
∠3 > ∠4 ...(ii)
Adding (i) and (ii), we get
∠1 + ∠3 > ∠2 + ∠4
∠A >∠C [This proves 1st part]
Now in ADB, AB is the smallest side
AD > AB
∠5 > ∠6 ...(iii)
and in BCD, CD is the greatest side
CD > BC ∠7 > ∠8 ...(iv)
Adding (iii) and (iv), we get:
∠5 + ∠7 > ∠6 + ∠8
∠B > ∠D [This proves 2nd part]
Hence ∠A > ∠C and ∠B > ∠D
[Hence Proved]
Question 34:
In fig. PR >PQ and PS bisects ∠QPR. Prove that ∠PSR > ∠PSQ.
Answer:
In PQR,
PR > PQ (given)
∠PQR > ∠PRQ
(∠opp. to longer side is greater) ...(1)
Again ∠1 = ∠2
[Since, PS is the bisector of ∠P] ...(2)
∠PQR + ∠1 > ∠PRQ + ∠2 ...(3)
But ∠PQS + ∠1 + ∠PSQ =
∠PRS + ∠2 + ∠PSR = 180
[Sum of ∠s of is 180]
∠PQR + ∠1 + ∠PSQ =
∠PRQ + ∠2 + ∠PSR ...(4)
[Since ∠PRS = ∠PRQ and
∠PQS = ∠PQR]
From (3) and (4), we get
∠PSQ < ∠PSR
or ∠PSR > ∠PSQ
Question 35:
Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
Answer:
Given: l is a line and P is point not lying on l.
PM l.
N is any point on l other than M.
To prove: PM < PN
Proof: In PMN, ∠M is the right angle. So, N is an acute angle.
(Angle sum property of triangle)
∠M > ∠N.
PN > PM (Side opp. greater angle)
or PM < PN.
Hence, of all line segments drawn from a given point not on it, the perpendicular is
the shortest.
Question 36:
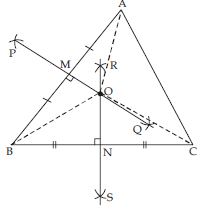
ABC is a triangle. Locate a point in the interior of ABC which is equidistant from all the vertices of ABC.
Answer:
Let ABC be a triangle.
Draw perpendicular bisectors PQ and RS of sides AB and BC respectively of triangle ABC.
Let PQ bisects AB at M and RS bisects BC at point N.
Let PQ and RS intersect at point O.
Join OA, OB and OC.
Now in AOM and BOM
AM = MB (By construction)
∠AMO = ∠BMO
(each = 90) [By construction]
OM = OM (Common)
AOM BOM
(SAS criteria of congruency)
So, OA = OB (c.p.c.t.) ....(i)
Similarly, BON CON
OB = OC (c.p.c.t) ....(ii)
From (i) and (ii), we observe that
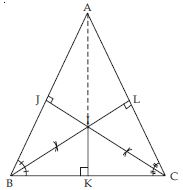
OA = OB = OC
Hence, O is the point of intersection of perpendicular bisectors of any two sides of ABC equidistant from its vertices.
Question 37:
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
Answer:
Let ABC be a triangle.
Draw bisectors of ∠B and ∠C.
Let these angle bisectors intersect each other at
point I.
Draw IK BC
Also draw IJ AB
and IL AC
Join AI.
In BIK and BIJ,
∠IKB = ∠IJB (each = 90)
(By construction)
∠IBK = ∠IBJ
[ BI is the bisector of ∠B]
(By construction)
BI = BI (Common)
BIK BIJ
(AAS criteria of congruency)
IK = IJ
(Congruent parts of congruent triangles) ....(i)
Similarly, CIK CIL
So IK = IL (c.p.c.t) ....(ii)
From (i) and (ii), we get:
IJ = IK = IL ;
Hence, I is the point of intersection of angle bisectors of any two angles of ABC equidistant from its sides.
Question 38:
In a huge park, people are concentrated at three points (see fig.).
A: where there are different slides and swings for children.
B: near which a man-made lake is situated.
C: which is near to a large parking and exit.
Where should an icecream parlour be set up so that maximum number of persons can approach
it?
Answer:
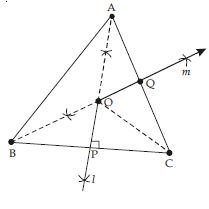
The parlour should be equidistant from A, B
and C.
For this let we draw perpendicular bisector say l of line joining points B and C also draw
perpendicular bisector say m of line joining points A and C.
Let l and m intersect each other at point O.
Now point O is equidistant from points A, B and C.
Join OA, OB and OC.
Proof: In BOP and COP
OP = OP (Common)
∠OPB = ∠OPC (each = 90)
(By Const.)
BP = PC
[ P is the mid-point of BC]
BOP COP
[SAS criteria of congruency]
So OB = OC (c.p.c.t.) ...(i)
Similarly AOQ COQ
OA = OC (c.p.c.t.) ..(ii)
From (i) and (ii), we get:
OA = OB = OC
We observe that ice-cream parlour should be set up at point O; the point of intersection of
perpendicular bisectors of any two sides out of three formed by joining these points.
Question 39:
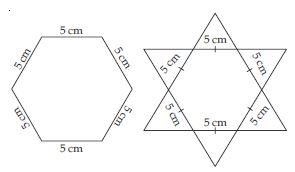
Complete the hexagonal and star shaped Rangolies (see figs.) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?
Answer:
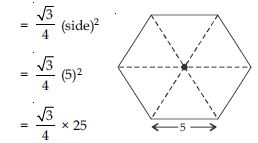
In hexagonal rangoli: Number of equilateral triangles each of side 5 cm = 6
Area of equilateral triangle of side 5 cm
Area of hexagonal rangoli = 6 × area of an equilateral triangle
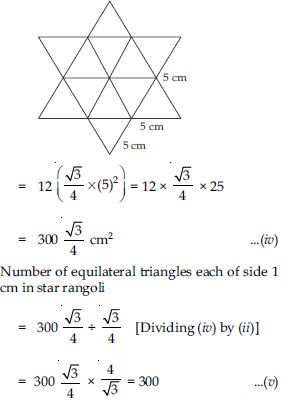
Now in Star Rangoli
Number of equilateral triangles each of side 5 cm = 12
So, total area of star rangoli = 12 × area of an equilateral triangle of side 5 cm
From (iii) and (v), we observe that star rangoli has more equilateral triangles each of side 1 cm.