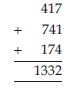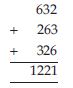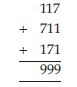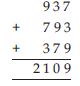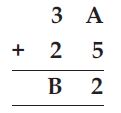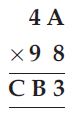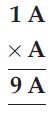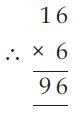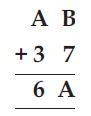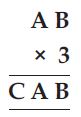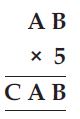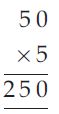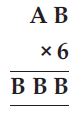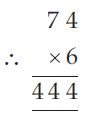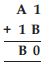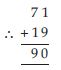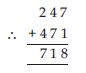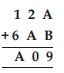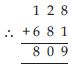Question 1:
Write 25 in generalised form.
Answer:
25 = 20 + 5 = (2 × 10) + 5 × 1
Question 2:
Write 73 in generalised form.
Answer:
73 = 70 + 3 = (7 × 10) + 3 × 1
Question 3:
Write 129 in generalised form.
Answer:
129 = 100 + 20 + 9
= (1 × 100) + (2 × 10) + 9 × 1
Question 4:
Write 302 in generalised form.
Answer:
302 = 300 + 0 + 2
= (3 × 100) + (10 × 0) + 2 × 1
Question 5:
Write 10 × 5 + 6 in the usual form.
Answer:
10 × 5 + 6 = 50 + 6 = 56
Question 6:
Write 100 × 7 + 10 × 1 + 8 in the usual form.
Answer:
100 × 7 + 10 × 1 + 8 = 700 + 10 + 8 = 718
Question 7:
Write 100 × a + 10 × c + b in the usual form.
Answer:
100 × a + 10 × c + b = 100a + 10c + b = acb
Question 8:
Take a 2-digit number 27.
Now reverse the digits of the number, and add them.
Now divide your answer by 11.
What do you observe?
Answer:
27
Here, 27 + 72 = 99
99 11 = 9
Also, 2 + 7 = 9
i.e. the quotient is equal to the sum of the digits of the number he chose.
Question 9:
Take a 2-digit number 39.
Now reverse the digits of the number, and add them.
Now divide your answer by 11.
What do you observe?
Answer:
39
Here, 39 + 93 = 132
132 11 = 12
Also, 3 + 9 = 12
i.e., the quotient is equal to the sum of the digits of the number he chose.
Question 10:
Take a 2-digit number 64.
Now reverse the digits of the number, and add them.
Now divide your answer by 11.
What do you observe?
Answer:
64
Here, 64 + 46 = 110
110 11 = 10
Also, 6 + 4 = 10
i.e., the quotient is equal to the sum of the digits of the number he chose.
Question 11:
Take a 2-digit number 17.
Now reverse the digits of the number, and add them.
Now divide your answer by 11.
What do you observe?
Answer:
17
Here, 17 + 71 = 88
88 11 = 8
Also, 1 + 7 = 8
i.e., the quotient is equal to the sum of the digits of the number he chose.
Question 12:
Take a 2-digit number 17.
Now reverse the digits of the number, and subtract the smaller number from the larger one.
Now divide your answer by 9.
What do you observe?
Answer:
17
On reversing the digits, we have : 71
71 - 17 = 54
Now, 54 9 = 6.
Also, 7 - 1 = 6.
i.e., the quotient is the difference between the
digits of the number he chose.
Question 13:
Take a 2-digit number 21.
Now reverse the digits of the number, and subtract the smaller number from the larger one.
Now divide your answer by 9.
What do you observe?
Answer:
21
On reversing the digits, we have; 12
21 - 12 = 9
Now, 9 9 = 1
Also, 2 - 1 = 1
i.e., the quotient is the difference between the digits of the number he chose.
Question 14:
Take a 2-digit number 96.
Now reverse the digits of the number, and subtract the smaller number from the larger one.
Now divide your answer by 9.
What do you observe?
Answer:
96
On reversing the digits, we have : 69
96 - 69 = 27
Now, 27 9 = 3
Also, 9 - 6 = 3
i.e., the quotient is the difference between the digits of the number he chose.
Question 15:
Take a 2-digit number 37.
Now reverse the digits of the number, and subtract the smaller number from the larger one.
Now divide your answer by 9.
What do you observe?
Answer:
37
On reversing the digits, we have : 73.
73 - 37 = 36
Now, 36 9 = 4
Also, 7 - 3 = 4
i.e., the quotient is the difference between the digits of the number he chose.
Question 16:
Take a 3-digit number 132.
Now make a new number by putting the digits in reverse order, and subtract the smaller number from the larger one.
Divide your answer by 99.
What do you observe?
Answer:
132
On reversing the digits, we have : 231
Difference = 231 - 132 = 99
Now, 99 99 = 1
Also, 2 - 1 = 1
i.e., the quotient is equal to the difference between the hundreds digit and the ones digit.
Question 17:
Take a 3-digit number 469.
Now make a new number by putting the digits in reverse order, and subtract the smaller number from the larger one.
Divide your answer by 99.
What do you observe?
Answer:
469
On reversing the digits, we have; 964.
Difference = 964 - 469 = 495
Now, 495 99 = 5
Also, 9 - 4 = 5
i.e., the quotient is equal to the difference between the hundreds digits and the ones digit.
Question 18:
Take a 3-digit number 737.
Now make a new number by putting the digits in reverse order, and subtract the smaller number from the larger one.
Divide your answer by 99.
What do you observe?
Answer:
737
On reversing the digits, we have; 737
Difference = 737 - 737 = 0
Now, 0 99 = 0
Also, 7 - 7 = 0
i.e., the quotient is equal to the difference between the hundreds digits and the ones digit.
Question 19:
Take a 3-digit number 901.
Now make a new number by putting the digits in reverse order, and subtract the smaller number from the larger one.
Divide your answer by 99.
What do you observe?
Answer:
901
On reversing the digits, we have; 109.
Difference = 901 - 109 = 792
Now, 792 99 = 8
Also, 9 - 1 = 8
i.e., the quotient is equal to the difference between the hundreds digits and the ones digit.
Question 20:
Take a 3-digit number 417.
Now use this number to form two more 3-digit numbers, like this: if the number you chose is abc, then the first number is cab (i.e., with the ones digit shifted to the “left end” of the number) and the other number is bca (i.e., with the hundreds digit shifted to the “right end” of the number).
Now add them up.
Divide the resulting number by 37.
What do you observe?
Answer:
417
Here; 417
Now take; 741
[i.e., the ones digit shifted to the “left end” of the number.]
Then; 174
[i.e., the hundreds digit shifted to the “right end” of the number.]
On adding all these three numbers, we have;
On dividing this number by 37, we have;
i.e., 1332 37 = 36 (No remainder).
Question 21:
Take a 3-digit number 632.
Now use this number to form two more 3-digit numbers, like this: if the number you chose is abc, then the first number is cab (i.e., with the ones digit shifted to the “left end” of the number) and the other number is bca (i.e., with the hundreds digit shifted to the “right end” of the number).
Now add them up.
Divide the resulting number by 37.
What do you observe?
Answer:
632
Here; 632
Now take; 263
[i.e., the ones digit shifted to the “left end” of the number.]
Then; 326
[i.e., the hundreds digit shifted to the “right end” of the number.]
On adding all these three numbers, we have;
On dividing this number by 37, we have;
i.e., 1221 37 = 33 (No remainder).
Question 22:
Take a 3-digit number 117.
Now use this number to form two more 3-digit numbers, like this: if the number you chose is abc, then the first number is cab (i.e., with the ones digit shifted to the “left end” of the number) and the other number is bca (i.e., with the hundreds digit shifted to the “right end” of the number).
Now add them up.
Divide the resulting number by 37.
What do you observe?
Answer:
117
Here; 117
Now take; 711
[i.e., the ones digit shifted to the “left end” of the number.]
Then; 171
[i.e., the hundreds digit shifted to the “right end” of the number.]
On adding all these three numbers, we have;
On dividing this number by 37, we have; i.e., 999 37 = 27 (No remainder).
Question 23:
Take a 3-digit number 937.
Now use this number to form two more 3-digit numbers, like this: if the number you chose is abc, then the first number is cab (i.e., with the ones digit shifted to the “left end” of the number) and the other number is bca (i.e., with the hundreds digit shifted to the “right end” of the number).
Now add them up.
Divide the resulting number by 37.
What do you observe?
Answer:
937
Here; 937
Now take; 793
[i.e., the ones digit shifted to the “left end” of the number.]
Then; 379
[i.e., the hundreds digit shifted to the “right end” of the number.]
On adding all these three numbers, we have;
On dividing this number by 2109 by 37, we have;
i.e., 2109 37 = 57 (No remainder)
Question 24:
Write a 2-digit number ab and the number obtained by reversing its digits, i.e., ba. Find their sum. Let the sum be a 3-digit number, dad
i.e., ab + ba = dad
(10a + b) + (10b + a) = dad
11(a + b) = dad
The sum a + b cannot exceed 18 (Why?)
Is dad a multiple of 11?
Is dad less than 198?
Write all the 3-digit numbers which are multiples of 11 up to 198.
Find the values of a and d.
Answer:
Let the two digit number be ab and the number
obtained by reversing its digits is ba.
Let their sum a 3-digit number be dad.
ab + ba = dad
(10a + b) + (10b + a) = dad
11(a + b) = dad
The sum a + b cannot exceed 18, because the
greatest 2-digit number can be 99 so that 99 +
99 = 198.
Yes, these number 198 is clearly a multiple of 11.
All the 3-digit numbers which are the multiples
of 11 are 110, 121, 132, 143, 154, 165, 176, 187 and 198.
Clearly, dad = 121
a = 2, d = 1.
Question 25:
Find the values of the letters in each of the following and give reasons for the steps involved.
Answer:
Here, we have to find the values of letters A
and B.
Since, the ones digits of (A + 5) is 2.
Which is possible only when A is 7 i.e., 7 + 5
= 12
Also, Ten’s digit and carry digit = 3 + 2 + 1 = B
( carry is 1)
5 + 1 = B
B = 6
A = 7, B = 6.
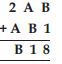
Question 26:
Find the values of the letters in each of the following and give reasons for the steps involved.
Answer:
Here, we have to find the values of letters A,
B and C.
Since the ones digit of (A + 8) is 3.
Which is possible, only when, A is 5 i.e., (5 + 8)
= 13.
Also, Ten’s digit and hundreds digit
= 4 + 9 = CB
= 13 + 1 = CB [ carry is 1]
14 = CB
C = 1, B = 4
A = 5, B = 4, C = 1.
Question 27:
Find the values of the letters in each of the following and give reasons for the steps involved.
Answer:
Here, we have to find the value of letter A. Since,
the ones digit of A × A = A.
A may have the values either A = 1, 5, 6.
But the tens digit is 9, which is possible only for
value A = 6.
Question 28:
Find the values of the letters in each of the following and give reasons for the steps involved.
Answer:
Here, B + 7 = A and A + 3 = 6
which means, we have
A = 2, B = 5
Question 29:
Find the values of the letters in each of the following and give reasons for the steps involved.
Answer:
Here, we have to find the values of letters A, B and C.
The unit and ten’s digit of product AB × 3 = CAB
Which is possible only when; 50 × 3 = 150
A = 5, B = 0 and C = 1.
Question 30:
Find the values of the letters in each of the following and give reasons for the steps involved.
Answer:
Here, AB × 5 = CAB
It means, the units digit and hundreds digit
should be same as that of the two digit no.
which is to be multiplied by 5, which is
possible only if; A = 2, B = 5 and C = 1
Alternate Solution
AB × 5 = CAB
Which is possible if
A = 5, B = 0 and C = 2
So, AB = 50
and CAB = 250
Question 31:
Find the values of the letters in each of the following and give reasons for the steps involved.
Answer:
Here, we have two missing entries A and B.
As it is given that; AB × 6 = BBB,
which is possible only when, A = 7 and B = 4
i.e., 74 × 6 = 444
Question 32:
Find the values of the letters in each of the following and give reasons for the steps involved.
Answer:
Here, it is given that; 1 + B = 0,
which is only possible, when B = 9 i.e., 1 + 9 = 10
and A + 1 = B A + 1 = 9
which means A must be 7
Because, 7 + 1 + 1 (carry) = 9
i.e., A = 7 and B = 9
Question 33:
Find the values of the letters in each of the following and give reasons for the steps involved.
Answer:
Here, the missing entries are A and B.
As B + 1 = 8 the possible value of B is 7
and A + B = 1, also B = 7
A must be 4, which gives sum as 11.
2 + A = B 2 + 4 + (1 carry) = 7
i.e., A = 4 and B = 7
Question 34:
Find the values of the letters in each of the following and give reasons for the steps involved.
Answer:
Here, the missing entries are A and B.
It is given that; 2 + A = 0 2 + 8 = 10
Also, 1 + 6 = A
But A = 8; 1 + 6 + (1 carry) = 8 = A
And A + B = 9 8 + B = 9 B = 1
i.e., A = 8, B = 1
Question 35:
If the division N 5 leaves a remainder of 3,
what might be the ones digit of N?
Answer:
The ones digit, when divided by 5, must leave a remainder of 3. So, the ones digit must be either 3 or 8.
Question 36:
If the division N 5 leaves a remainder of 1,
what might be the ones digit of N?
Answer:
The ones digit, when divided by 5, must leave a remainder of 1. So, the ones digit must be either 1 or 6.
Question 37:
If the division N 5 leaves a remainder of 4, what might be the ones digit of N?
Answer:
The ones digit, when divided by 5, must leave a remainder of 4. So, the ones digit must be either 4 or 9.
Question 38:
If the division N 2 leaves a remainder of 1,
what might be the ones digit of N?
Answer:
N is odd, so its ones digit is odd.
Therefore, the ones digit must be 1, 3, 5, 7 or 9.
Question 39:
If the division N 2 leaves no remainder (i.e., Zero remainder) what might be the ones digit of N?
Answer:
N is an even number, so its units digit is also an even number. Therefore, the ones digit must be 2, 4, 6, 8 or 0.
Question 40:
Check the divisibility of the following numbers by 9.
1. 108, 2. 616, 3. 294, 4. 432, 5. 927.
Answer:
1. 108.
The sum of the digits of 108 is 1 + 0 + 8 = 9.
As this number is divisible by 9.
The number 108 is divisible by 9.
2. 616.
The sum of the digits of 616 is 6 + 1 + 6 = 13.
As this number is not divisible by 9.
The number 616 is not divisible by 9.
3. 294.
The sum of the digits of 294 is 2 + 9 + 4 = 15.
As this number is not divisible by 9.
The number 294 is not divisible by 9.
4. 432.
The sum of the digits of 432 is 4 + 3 + 2 = 9.
As this number is divisible by 9.
The number 432 is divisible by 9.
5. 927.
The sum of the digits of 927 is 9 + 2 + 7 = 18
As this number is divisible by 9.
The number 927 is divisible by 9.
Question 41:
You have seen that a number 450 is divisible
by 10. It is also divisible by 2 and 5 which
are factors of 10. Similarly, a number 135 is
divisible by 9. It is also divisible by 3 which
is a factor of 9.
Can you say that if a number is divisible by
any number m, then it will also be divisible
by each of the factors of m?
Answer:
Yes, we can say that if a number is divisible by any number m, then it will also be divisible by each of the factors of m.
Question 42:
(i) Write a 3-digit number abc as
100a + 10b + c = 99a + 11b + (a - b + c)
= 11 (9a + b) + (a - b + c)
If the number abc is divisible by 11, then
what can you say about (a - b + c)?
Is it necessary that (a + c - b) should be divisible by 11?
(ii) Write a 4-digit number abcd as
1000a + 100b + 10c + d
= (1001a + 99b + 11c) - (a - b + c - d)
= 11 (91a + 9b + c) + [(b + d) - (a + c)]
If the number abcd is divisible by 11, then
what can you say about [(b + d) - (a + c)] ?
(iii) From (i) and (ii) above, can you say that
a number will be divisible by 11 if the
difference between the sum of digits at its
odd places and that of digits at the even
places is divisible by 11 ?
Answer:
(i) It is necessary that (a + c - b) should be
divisible by 11.
(ii) Yes, we can say that if the number abcd is
divisible by 11, then [(b + d) - (a + c)] must
be divisible by 11.
(iii) Yes, from (i) and (ii) above we can say
that a number will be divisible by 11 if the
difference between the sum of digits of its
odd places and that of digits at the even
places is divisible by 11.
Question 43:
Check the divisibility of the following numbers by 3.
1. 108 2. 616 3. 294 4. 432 5. 927
Answer:
Question 44:
If 21y5 is a multiple of 9, where y is a digit,
what is the value of y.
Answer:
Since 21y5 is a multiple of 9
Its sum of digits 2 + 1 + y + 5 = 8 + y is a
multiple of 9.
As y is a digit.
So, 8 + y = 9 y = 1
Therefore, y = 1
Question 45:
If 31z5 is a multiple of 9, where z is a digit,
what is the value of z.
You will find that there are two answers for the last problem. Why is this so?
Answer:
Since, 31z 5 is a multiple of 9.
Its sum of digits 3 + 1 + z + 5 = 9 + z is a
multiple of 9.
As z is a digit.
So, 9 + z is either 0 or 9.
9 + 0 = 9 and 9 + 9 = 18 = 1 + 8 = 9
z = 0 or z = 9.
Question 46:
If 24x is a multiple of 3, where x is a digit,
what is the value of x?
Answer:
Since 24x is a multiple of 3.
Its sum of digits = 2 + 4 + x = 6 + x is a multiple
of 3.
So, 6 + x is one of these numbers; 0, 3, 6, 9, 12,
15, 18 ............,
But, since x is a digit, it can only be that ;
6 + x = 6 or 9 or 12 or 15.
Therefore, x = 0 or 3 or 6 or 9.
Thus, x can have any four different values.
Question 47:
If 31z5 is a multiple of 3, where z is a digit,
what might be the values of z.
Answer:
Since, 31z 5 is a multiple of 3.
Its sum of digits = 3 + 1 + z + 5 = 9 + z.
Since, the sum (9 + z) is a multiple of 3 and z is a digit.
z can have the values either 0 or 3 or 6 or 9.