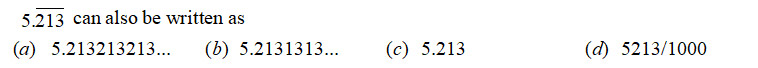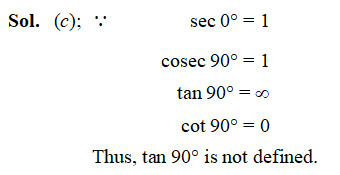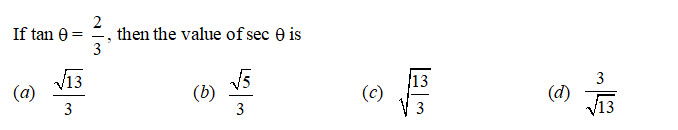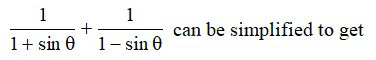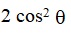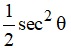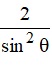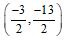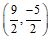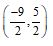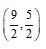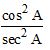Board Paper of Class 10 2022 Mathematics (Basic) Term 1 Set 4 - Solutions

General Instructions:

This question paper contains 50 questions out of which 40 questions are to be attempted. All questions carry equal marks.

This question paper contains three Sections: A, B, and C.

Section A has 20 questions. Attempt any 16 questions from Q.No. 1 to 20.

Section B has 20 questions. Attempt any 16 questions from Q.No. 21 to 40.

Section C contains two Case Studies containing 5 Questions in each case. Attempt any 4 questions from Q.No. 41 to 45 and 4 another from Q.No. 46 to 50.

There is only one correct option for every multiple choice question (MCQ). Marks will not be awarded for answering more than one option.

There is no negative marking.

SECTION A

(In this section, there are 20 questions. Any 16 are to be attempted).

Question 1

HCF of 92 and 152 is

Sol. (a);

The prime factorisation of 92 and 152 are:

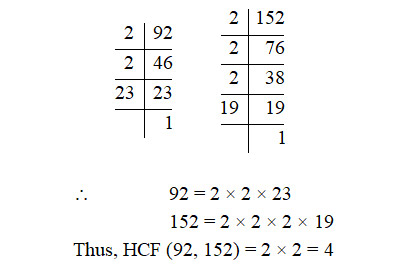
$Q1 Solution1$

Solutions

Question 2

In $△$ ABC, DE || BC, AD = 4 cm, DB = 6 cm and AE = 5 cm. The length of EC is

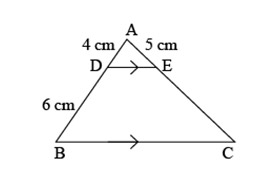
7 cm
6.5 cm
7.5 cm
8 cm

Sol. (c); In $△$ ABC, DE || BC by BPT

Solutions

Question 3

The value of k, for which the pair of linear equations x + y – 4 = 0, 2x + ky – 3 = 0 have no solution, is

Sol. (b); Since the given pair of linear equations has no solution.

$Q3$

Solutions

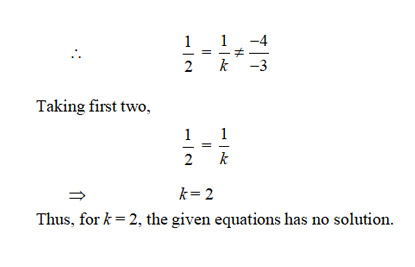
Question 4

The value of (tan² 45^° – cos² 60^°) is

$\begin{matrix} 1 \\ - \\ 2 \end{matrix}$
$\begin{matrix} 1 \\ - \\ 4 \end{matrix}$
$\begin{matrix} 3 \\ - \\ 2 \end{matrix}$
$\begin{matrix} 3 \\ - \\ 4 \end{matrix}$

Sol. (d); We know that,

$Q4$

Solutions

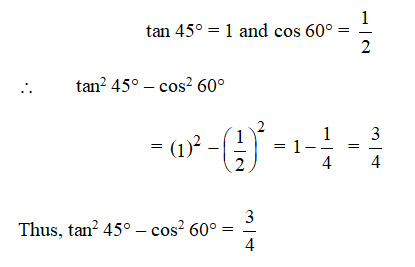
Question 5

A point (x, 1) is equidistant from A(0, 0) and B(2, 0). The value of x is

1
0
2
$\begin{matrix} 1 \\ - \\ 2 \end{matrix}$

Sol. (a); Let P(x, 1) be equidistant from A(0, 0) and B(2, 0)

$Q4$

Solutions

Question 6

Two coins are tossed together. The probability of getting exactly one head is

$\begin{matrix} 1 \\ - \\ 4 \end{matrix}$
$\begin{matrix} 1 \\ - \\ 2 \end{matrix}$
$\begin{matrix} 3 \\ - \\ 4 \end{matrix}$
1

Sol. (b); When two coins are tossed together, then the following outcomes are obtained

HH, HT, TH, TT

Exactly one head is obtained, if the events are:

HT, TH

Hence, P(exactly one head) $\begin{matrix} 2 & 1 \\ = & - & = & - \\ 4 & 2 \end{matrix}$

Solutions

Question 7

A circular arc of length 22 cm subtends an angle $θ$ at the centre of the circle of radius 21 cm. The value of $θ$ is

$Q7$

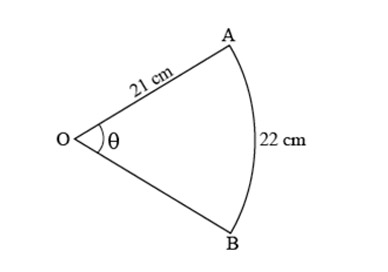
90°
50°
60°
30°

(c); Length of arc (l) = 22 cm

Solutions

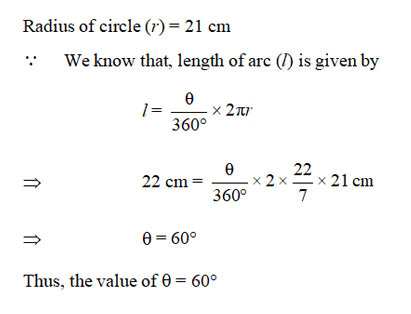
Question 8

A quadratic polynomial having sum and product of its zeroes as 5 and 0 respectively, is

x² + 5x
2x(x – 5)
5x² - 1
x² – 5x + 5

Sol. (b); Let $α$ and $β$ be two roots of the given polynomial.

Solutions

Question 9

If P(E) = 0.65, then the value of P(not E) is

1.65
0.25
0.65
0.35

Sol. (d); We know that, sum of the probability of happening event (E) and not happening event ( $\bar{E}$ ) is 1.

Solutions

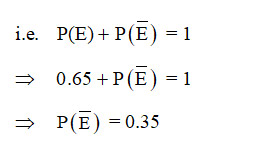
Question 10

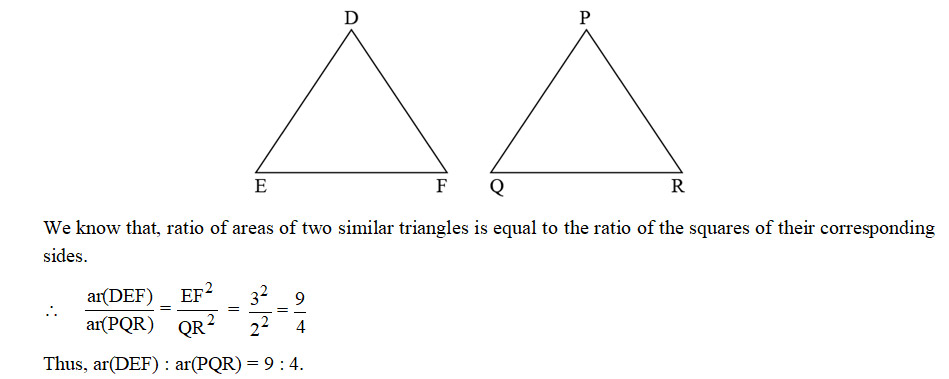
It is given that $△$ DEF ~ $△$ PQR. EF : QR = 3 : 2, then value of ar(DEF): ar(PQR) is

4 : 9
4 : 3
9 : 2
9 : 4

Sol. (d); Given that $△$ DEF ~ $△$ PQR and EF : QR = 3 : 2

Solutions

Question 11

Zeroes of a quadratic polynomial x² – 5x + 6 are

–5, 1
5, 1
2, 3
–2, –3

Sol. (c); Given quadratic polynomial is

Solutions

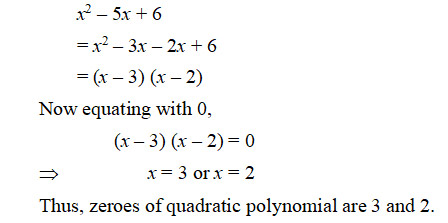
Question 12

$\begin{matrix} 57 \\ - \\ 300 \end{matrix}$ is a

non-terminating and non-repeating decimal expansion.
terminating decimal expansion after 2 places of decimals.
terminating decimal expansion after 3 places of decimals.
non-terminating but repeated decimal expansion.

Solutions

Question 13

Perimeter of a rectangle whose length ( $l$ ) is 4 cm more than twice its breadth (b) is 14 cm. The pair of linear equations representing the above information is

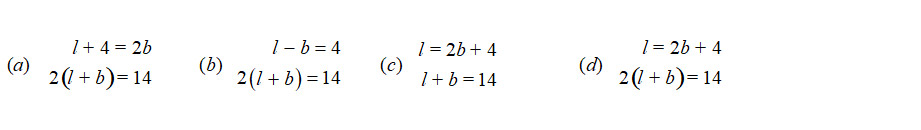
Sol.(d); Let $l$ be the length and $b$ be the breadth.

Solutions

Question 14

Solutions

Question 15

The ratio in which the point (4, 0) divides the line segment joining the points (4, 6) and (4, –8) is

1 : 2
3 : 4
4 : 3
1 : 1

Sol. (b); Let P(4, 0) divides the line segment joining the points A(4, 6) and B(4, –8) in the ratio k : 1.

Solutions

Question 16

Solutions

Question 17

In the given figure, a circle is touching a semi-circle at C and its diameter AB at O. If AB = 28 cm, what is the radius of the inner circle?

Solutions

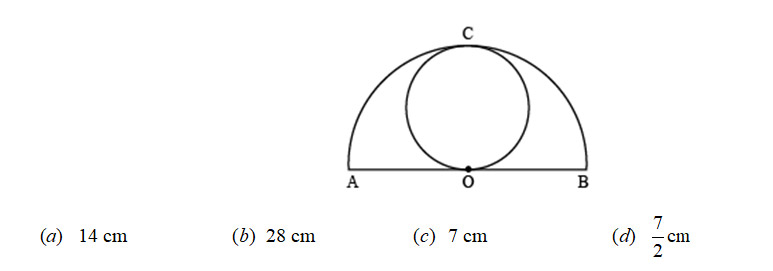
Question 18

The vertices of a triangle OAB are O(0, 0), A(4, 0) and B(0, 6). The median AD is drawn on OB. The length AD is

Solutions

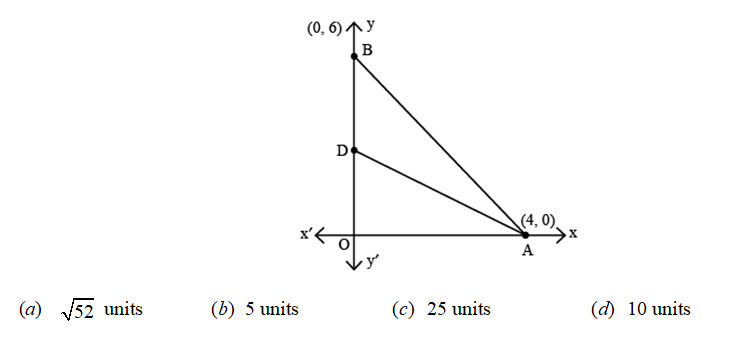
Question 19

Solutions

Question 20

Solutions

SECTION B

(In this section, there are 20 questions. Any 16 are to be attempted).

Question 21

The perimeter of the sector of a circle of radius 14 cm and central angle 45° is

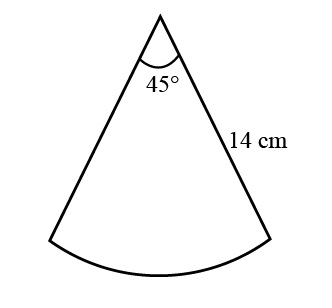
11 cm
22 cm
28 cm
39 cm

Sol. (d);

$Q21 Solution1$

Solutions

Question 22

A bag contains 16 red balls, 8 green balls and 6 blue balls. One ball is drawn at random. The probability that it is blue ball is

1/2
1/5
1/30
5/6

Sol. (b);

Total number of balls in the bag = 16 + 8 + 6 = 30

Number of blue balls in the bag = 6

Solutions

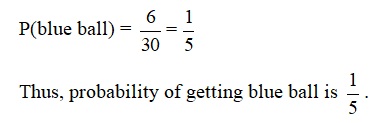
Question 23

If sin $θ$ - cos $θ$ = 0, then the value of $θ$ is

30°
45°
90°
0°

Sol. (b); Given sin $θ$ - cos $θ$ = 0

Since, we know that sine and cosine have equal value at 45°.

Thus, $θ$ = 45°.

Solutions

Question 24

The probability of happening of an event is 0.02. The probability of not happening of the event is

0.02
0.80
0.98
49/100

Sol. (c); We know that, sum of the probability of happening and not happening of an event is 1.

Solutions

Question 25

Two concentric circles are centred at O. The area of shaded region, if outer and inner radii are 14 cm and 7 cm respectively, is

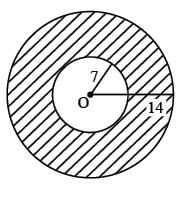
462 cm²
154 cm²
231 cm²
308 cm²

(a); Outer radius (R) = 14 cm

$Q25$

Solutions

Question 26

Sol. (d);

$Q7$

Solutions

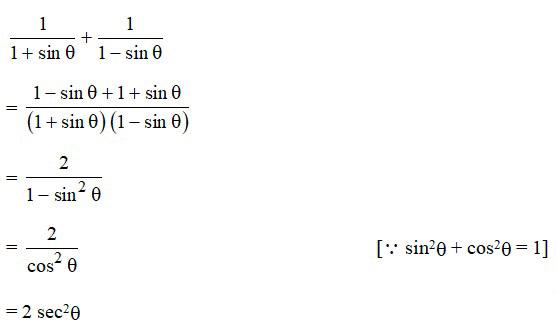
Question 27

The origin divides the line segment AB joining the points A(1, -3) and B(-3, 9) in the ratio:

3 : 1
1 : 3
2 : 3
1 : 1

Sol. (b); Let origin divides AB in the ratio k : 1.

Solutions

Question 28

The perpendicular bisector of a line segment A(–8, 0) and B(8, 0) passes through a point (0, k). The value of k is

0 only
0 or 8 only
any real number
any non-zero real number

Sol. (c); The coordinates of mid-point of line segment joining A(–8, 0) and B(8, 0) =

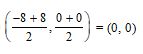
Since, given that perpendicular bisector AB passes through (0, k).

Thus, the value of k will be any real number as origin is the mid-point of AB.

Solutions

Question 29

Which of the following is a correct statement?

Two congruent figures are always similar.
Two similar figures are always congruent.
All rectangles are similar.
The polygons having same number of sides are similar.

Sol. (a);

Two congruent figures are always similar.
Two similar figures are not always congruent.
All rectangles are not similar.
The polygons having same number of sides are not similar.
Thus, the correct statement is ‘Two congruent figures are always similar.’

Solutions

Question 30

The solution of the pair of linear equations x = –5 and y = 6 is

(–5, 6)
(–5, 0)
(0, 6)
(0, 0)

Sol. (a); The graph of linear equations x = –5 and y = 6, intersect each other at (–5, 6).

Thus, the solution of the pair of linear equations x = –5 and y = 6 is (–5, 6).

Solutions

Question 31

A circle of radius 3 units is centered at (0, 0). Which of the following points lie outside the circle?

(–1, –1)
(0, 3)
(1, 2)
(3, 1)

Sol. (d); Radius of circle = 3 units

Solutions

Question 32

The value of k for which the pair of linear equation 3x + 5y = 8 and kx + 15y = 24 has infinitely many solutions, is

Sol. (b); The given pair of linear equations are

Solutions

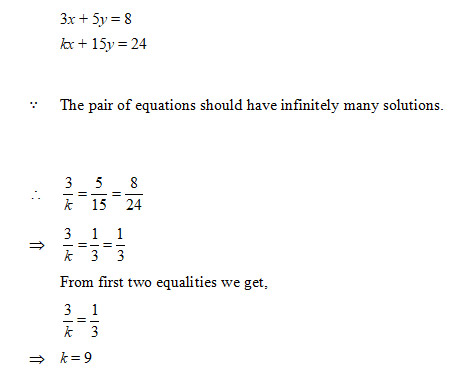
Question 33

HCF of two consecutive even number is

Sol. (c); HCF of two consecutive even numbers is 2.

Solutions

Question 34

The zeroes of quadratic polynomial x² + 99x + 127 are

both negative
both positive
one positive and one negative
reciprocal of each other

Sol. (a); Let $α$ and β zeroes of x² + 99x + 127.

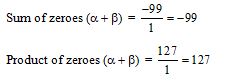
Since, sum of zeroes is negative but product of zeroes is positive.

Thus, both the zeroes of the given quadratic polynomial are negative.

Solutions

Question 35

The mid-point of line segment joining the points (–3, 9) and (–6, –4) is

Sol. (c); The coordinates of mid-point of line segment joining the points (–3, 9) and (–6, –4)

Solutions

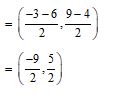
Question 36

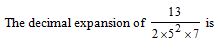
terminating after 1 decimal place.
non-terminating and non-repeating.
terminating after 2 decimal places.
non-terminating but repeating.

(d); A rational number having denominator, whose prime factors are not in the form 2^m × 5ⁿ, have non-terminating but repeating decimal expansion.

Solutions

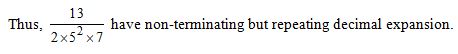
Question 37

In ΔABC, DE ‖ BC, AD = 2 cm, DB = 3 cm, DE : BC is equal to

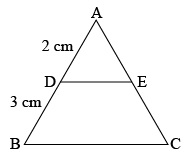
2 : 3
2 : 5
1 : 2
3 : 5

Sol. (b);

Solutions

Question 38

The (HCF x LCM) for the numbers 50 and 20 is

1000
50
100
500

Sol. (a); We know that,

Product of two numbers is equal to the product of their HCF and LCM.

Thus, HCF x LCM = 50 x 20 = 1000.

Solutions

Question 39

For which natural number n, 6ⁿ ends with digit zero?

6
5
0
None

Sol. (d);

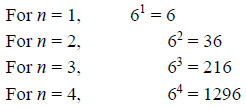
We observe that for any natural number n, 6ⁿ always ends with 6.

Thus, for no natural number n, 6ⁿ ends with digit zero.

Solutions

Question 40

(1 + tan² A) (1 + sin A) (1 – sin A) is equal to

Sol. (b); (1 + tan² A) (1 + sin A) (1 – sin A)

Solutions

SECTION C

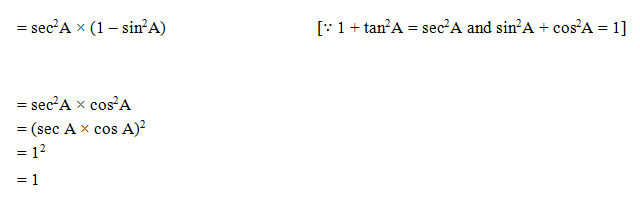
Case Study – I

(Attempt any 4 questions from Q. No. 41 to 45)

Sukriti throws a ball upwards, from a rooftop which is 8 m high from ground level. The ball reaches to some maximum height and then returns and hit the ground.

If height of the ball at time t ( in sec) is represented by h (m), then equation of its path is given as $h = - t^{2} + 2 t + 8$
Based above information, answer the following:

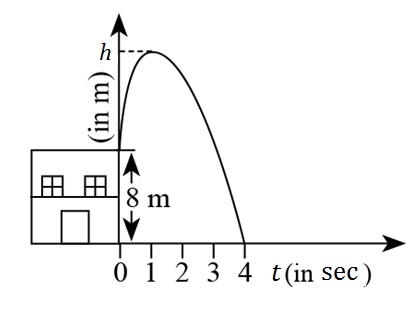
Question 41

The maximum height achieved by ball is

7 m
8 m
9 m
10 m

Sol. (c)

Draw a perpendicular from maximum height on x-axis. It meet x-axis at (1, 0).

$H e i g h t h = - t^{2} + 2 t + 8 (g i v e n)$

Thus, height of ball at time t = 1 is

$h = - {(1)}^{2} + 2 \times 1 + 8 = - 1 + 2 + 8 = 9 m .$

Solutions

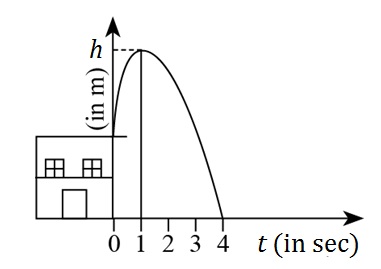
Question 42

The polynomial represented by above graph is

linear polynomial
quadratic polynomial
constant polynomial
cubic polynomial

Sol. (b) The polynomial represented by above graph is quadratic polynomial.

Solutions

Question 43

Time taken by ball to reach maximum height is

2 sec
4 sec.
1 sec.
2 min.

Sol. (c); Time taken by ball to reach maximum height is 1 sec.

Solutions

Question 44

Number of zeroes of the polynomial whose graph is given, is

Sol. (b) Since, given graph is of quadratic polynomial.

Thus, it has two zeros.

Solutions

Question 45

Zeroes of the polynomial are

4
–2, 4
2, 4
0, 4

Sol. (b); Given polynomial,

$- t^{2} + 2 t + 8 = - t^{2} + 4 t - 2 t + 8 = - t (t - 4) - 2 (t - 4) = (t - 4) (- t - 2)$

On equating to zero.

$(t - 4) (- t - 2) = 0 \Rightarrow t = 4, - 2 .$

Thus, zeroes of polynomial are –2, 4.

Solutions

Case Study- II

(Attempt any 4 questions from Q. No. 46 to 50)

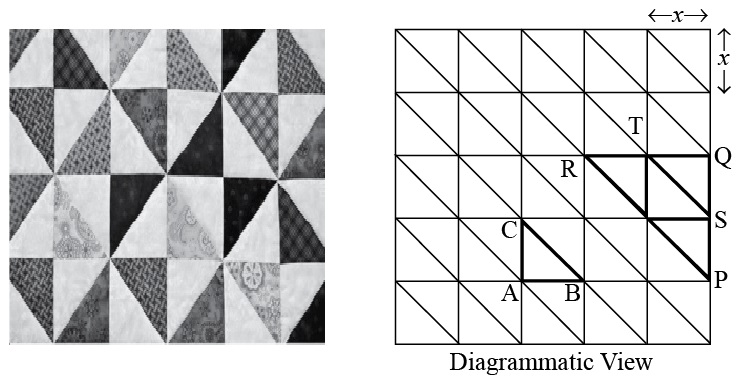
Quilts are available in various colours and design. Geometric design include shapes like squares, triangles, rectangles, hexagons etc. One such design shown above. Two triangles are highlighted, $△ A B C a n d △ P Q R$ .

Based on above information, answer the following questions:

Question 46

Which of the following criteria is not suitable for $△ ABC$ to be similar to $△ QRP$ ?

Sol. (d); RHS is not suitable for $△ ABC$ to be similar to $△ QRP$ .

Solutions

Question 47

If each square is of length x unit, then length BC is equal to

Sol. (a) In right $△ ABC, ∠ A = 90 °$

$∴ BC \sqrt{{AB}^{2} + {AC}^{2}} = \sqrt{x^{2} + x^{2}} = \sqrt{2 x^{2}} = x \sqrt{2} unit$

Solutions

Question 48

Ratio BC : PR is equal to

2 : 1
1 : 4
1 : 2
4 : 1

Sol. (c);

Solutions

Question 49

ar (PQR) : ar (ABC) is equal to

2 : 1
1 : 4
4 : 1
1 : 8

Sol. (c); $∵ △ ABC ~ △ QPR$

We know that, ratio of area of two similar triangles is equal to the ratio of square of corresponding sides.
Thus

$\frac{ar (△ QPR)}{ar (△ ABC)} = \frac{{PR}^{2}}{BC} = \frac{2^{2}}{12} = \frac{4}{1} = \frac{ar (△ PQR)}{ar (△ ABC)} [∵ ar (△ PQR) = ar (△ QPR)]$

Solutions

Question 50

Which of the following is not true?

$△ TQS ~ △ PQR$
$△ CBA ~ △ STQ$
$△ BAC ~ △ PQR$
$△ PQR ~ △ ABC$

Sol. (d); $∆ PQR ≁ ∆ ABC$

It should be $∆ QPR ~ ∆ ABC .$

Solutions

Board Paper of Class 10 2022 Mathematics (Basic) Term 1 Set 4 - Solutions

General Instructions:

SECTION A

Question 1

HCF of 92 and 152 is

Question 2

In △ABC, DE || BC, AD = 4 cm, DB = 6 cm and AE = 5 cm. The length of EC is

Question 3

The value of k, for which the pair of linear equations x + y – 4 = 0, 2x + ky – 3 = 0 have no solution, is

Question 4

The value of (tan2 45° – cos2 60°) is

Question 5

A point (x, 1) is equidistant from A(0, 0) and B(2, 0). The value of x is

Question 6

Two coins are tossed together. The probability of getting exactly one head is

Question 7

A circular arc of length 22 cm subtends an angle θ at the centre of the circle of radius 21 cm. The value of θ is

Question 8

A quadratic polynomial having sum and product of its zeroes as 5 and 0 respectively, is

Question 9

If P(E) = 0.65, then the value of P(not E) is

Question 10

It is given that △DEF ~ △PQR. EF : QR = 3 : 2, then value of ar(DEF): ar(PQR) is

Question 11

Zeroes of a quadratic polynomial x2 – 5x + 6 are

Question 12

57-300 is a

Question 13

Perimeter of a rectangle whose length (l) is 4 cm more than twice its breadth (b) is 14 cm. The pair of linear equations representing the above information is

Question 14

Question 15

The ratio in which the point (4, 0) divides the line segment joining the points (4, 6) and (4, –8) is

Question 16

Question 17

In the given figure, a circle is touching a semi-circle at C and its diameter AB at O. If AB = 28 cm, what is the radius of the inner circle?

Question 18

The vertices of a triangle OAB are O(0, 0), A(4, 0) and B(0, 6). The median AD is drawn on OB. The length AD is

Question 19

Question 20

SECTION B

Question 21

The perimeter of the sector of a circle of radius 14 cm and central angle 45° is

Question 22

A bag contains 16 red balls, 8 green balls and 6 blue balls. One ball is drawn at random. The probability that it is blue ball is

Question 23

If sinθ - cosθ = 0, then the value of θ is

Question 24

The probability of happening of an event is 0.02. The probability of not happening of the event is

Question 25

Two concentric circles are centred at O. The area of shaded region, if outer and inner radii are 14 cm and 7 cm respectively, is

Question 26

Question 27

The origin divides the line segment AB joining the points A(1, -3) and B(-3, 9) in the ratio:

Question 28

The perpendicular bisector of a line segment A(–8, 0) and B(8, 0) passes through a point (0, k). The value of k is

Question 29

Which of the following is a correct statement?

Question 30

The solution of the pair of linear equations x = –5 and y = 6 is

Question 31

A circle of radius 3 units is centered at (0, 0). Which of the following points lie outside the circle?

Question 32

The value of k for which the pair of linear equation 3x + 5y = 8 and kx + 15y = 24 has infinitely many solutions, is

Question 33

HCF of two consecutive even number is

Question 34

The zeroes of quadratic polynomial x2 + 99x + 127 are

Question 35

The mid-point of line segment joining the points (–3, 9) and (–6, –4) is

Question 36

Question 37

In ΔABC, DE ‖ BC, AD = 2 cm, DB = 3 cm, DE : BC is equal to

Question 38

The (HCF x LCM) for the numbers 50 and 20 is

Question 39

For which natural number n, 6n ends with digit zero?

Question 40

(1 + tan2 A) (1 + sin A) (1 – sin A) is equal to

SECTION C

Case Study – I

In $△$ ABC, DE || BC, AD = 4 cm, DB = 6 cm and AE = 5 cm. The length of EC is

The value of (tan² 45^° – cos² 60^°) is

A circular arc of length 22 cm subtends an angle $θ$ at the centre of the circle of radius 21 cm. The value of $θ$ is

It is given that $△$ DEF ~ $△$ PQR. EF : QR = 3 : 2, then value of ar(DEF): ar(PQR) is

Zeroes of a quadratic polynomial x² – 5x + 6 are

$\begin{matrix} 57 \\ - \\ 300 \end{matrix}$ is a

Perimeter of a rectangle whose length ( $l$ ) is 4 cm more than twice its breadth (b) is 14 cm. The pair of linear equations representing the above information is

If sin $θ$ - cos $θ$ = 0, then the value of $θ$ is

The zeroes of quadratic polynomial x² + 99x + 127 are

For which natural number n, 6ⁿ ends with digit zero?

(1 + tan² A) (1 + sin A) (1 – sin A) is equal to

Which of the following criteria is not suitable for $△ ABC$ to be similar to $△ QRP$ ?