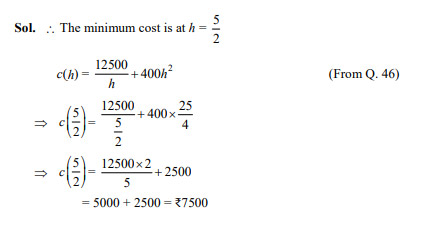Board Paper of Class 12 2021 Mathematics Term-1 Set-4 CODE 065/2/4

General Instructions:

This question paper comprises 50 questions out of which 40 questions are to be attempted as per instructions. All questions carry equal marks.

The question paper consists of three Sections - Section A, B and C.

Section - A contains 20 questions. Attempt any 16 questions from Q. No. 1 to 20.

Section - B also contains 20 questions. Attempt any 16 questions from Q. No. 21 to 40.

Section - C contains 10 questions including one Case Study. Attempt any 8 from Q. No. 41 to 50.

There is only one correct option for every Multiple Choice Question (MCQ). Marks will not be awarded for answering more than one option.

There is no negative marking.

SECTION A

SECTION-A

(In this section, there are 20 questions. Any 16 are to be attempted).

Question 1

Differential of $\log [\log ({logx}^{5})] w . r . t . x$ is

$\frac{5}{xlog (x^{5}) \log ({logx}^{5})}$
$\frac{5}{xlog (\log x^{5})}$
$\frac{5 x^{4}}{\log (x^{5}) \log (\log x^{5})}$
$\frac{5 x^{4}}{\log x^{5} \log (\log x^{5})}$

Ans. (a)

Solutions

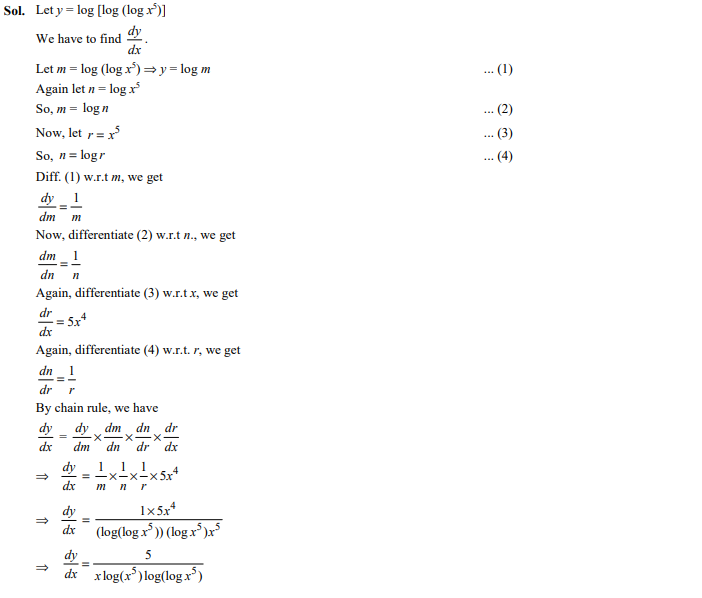
Question 2

The number of all possible matrices of order 2 × 3 with each entry 1 or 2 is

Ans. (c)

Sol: Number of elements in matrix of order 2 × 3 = 6
Number of all possible matrices = $2^{6}$ = 64

Solutions

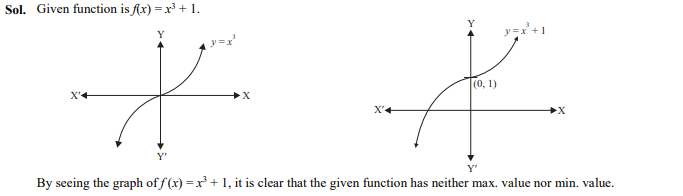
Question 3

A function $f : R \to R$ is defined as $f (x) = x^{3} + 1$ Then the function has

no minimum value
no maximum value
both maximum and minimum values
neither maximum value nor minimum value

Ans. (d)

Solutions

Question 4

If $s i n y = x c o s (a + y),$ then $\frac{d x}{d y}$ is

$\frac{\cos a}{\cos^{2} (a + y)}$
$\frac{- \cos a}{\cos^{2} (a + y)}$
$\frac{\cos a}{\sin^{2} y}$
$\frac{- \cos a}{\sin^{2} y}$

Ans.(a)

Solutions

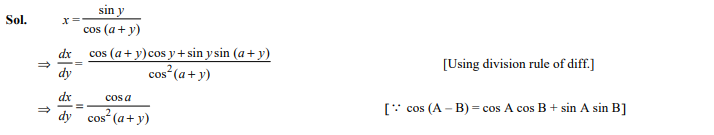
Question 5

The points on the curve $\frac{x^{2}}{9} + \frac{y^{2}}{25} = 1,$ where tangent is parallel to x-axis are

(±5, 0)
(0, ±5)
(0, ±3)
(±3, 0)

Ans. (b)

Solutions

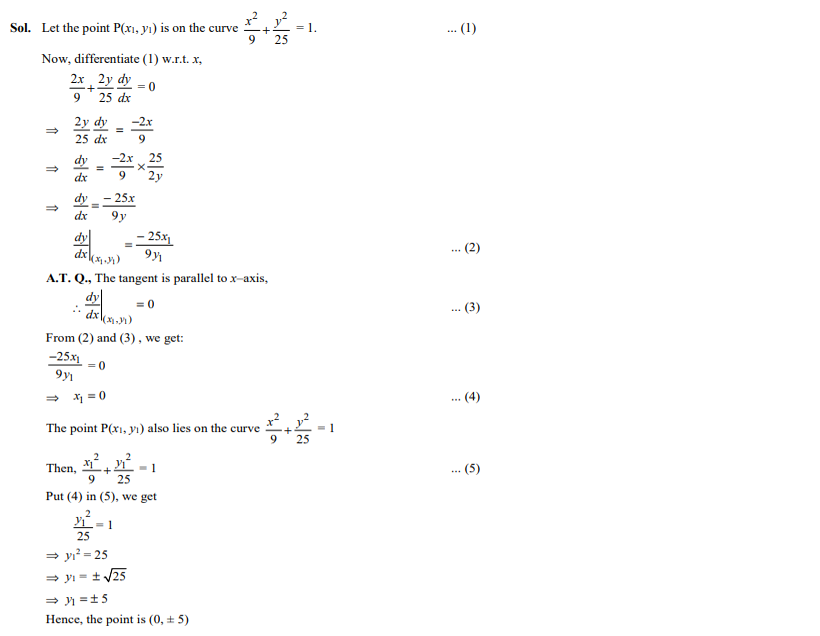
Question 6

Three points $P (2 x, x + 3), Q (0, x) a n d R (x + 3, x + 6)$ are collinear, then x is equal to

Ans. (d)

Solutions

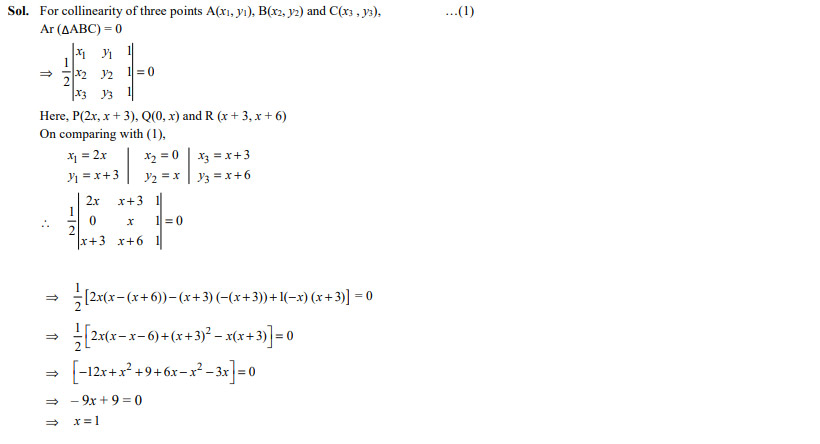
Question 7

The principal value of $\cos^{- 1} (\frac{1}{2}) + \sin^{- 1} (- \frac{1}{\sqrt{2}})$ is

$\frac{π}{3}$
$π$
$\frac{π}{3}$
$\frac{π}{6}$

Ans: (a)

Solutions

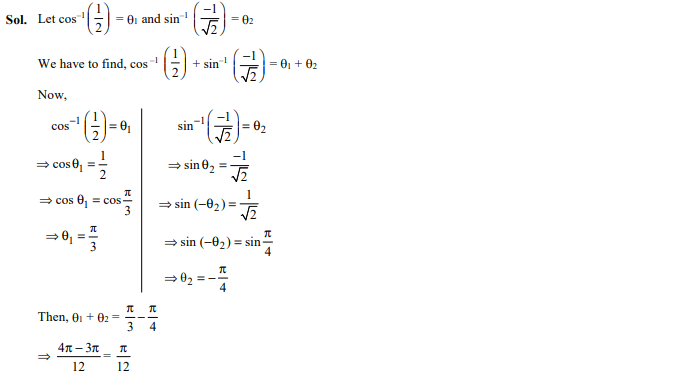
Question 8

If ${(x^{2} + y^{2})}^{2} = xy then \frac{dy}{dx} is$

$\frac{y + 4 x (x^{2} + y^{2})}{4 y (x^{2} + y^{2}) - x}$
$\frac{y - 4 x (x^{2} + y^{2})}{x + 4 (x^{2} + y^{2})}$
$\frac{y - 4 x (x^{2} + y^{2})}{4 y (x^{2} + y^{2}) - x}$
$\frac{4 y (x^{2} + y^{2}) - x}{y - 4 x (x^{2} + y^{2})}$

Ans. (c)

Solutions

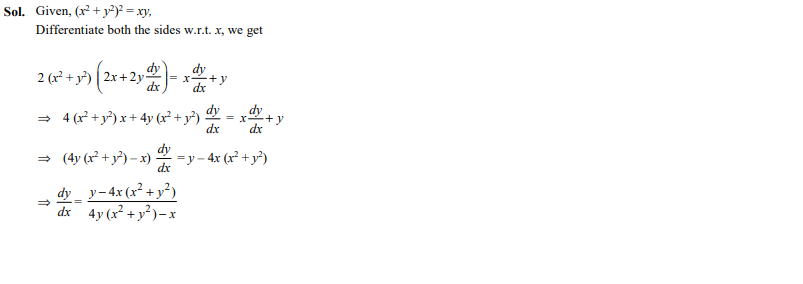
Question 9

If a matrix A is both symmetric and skew symmetric, then A is necessarily a

Diagonal matrix
Zero square matrix
Square matrix
Identity matrix

Ans. (b)

Solutions

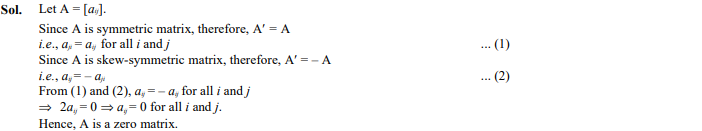
Question 10

Let set X = {1, 2, 3} and a relation R is defined in X as : R = {(1, 3), (2, 2), (3, 2)}, then minimum ordered pairs which should be added in relation R to make it reflexive and symmetric are

{(1, 1), (2, 3), (1, 2)}
{(3, 3), (3, 1), (1, 2)}
{(1, 1), (3, 3), (3, 1), (2, 3)}
{(1, 1), (3, 3), (3, 1), (1, 2)}

Ans. (c)

Sol. To make R reflexive: Add (3, 1), (2, 3) in the relation R.
To make R symmetric: Add (1, 1), (3, 3) in the relation R.
$∴$ The ordered pairs should be added in Relation ‘R’ are {(1, 1) (3, 3) (3, 1), (2, 3)}.

Solutions

Question 11

Ans. (b)

Solutions

Question 12

The function $f (x) = {\begin{cases} \frac{e^{3 x} - e^{- 5 x}}{x}, if x \neq 0 \\ k, if x = 0 \end{cases}$ is continuous at x = 0 for the value of k, as

Ans.(d)

Solutions

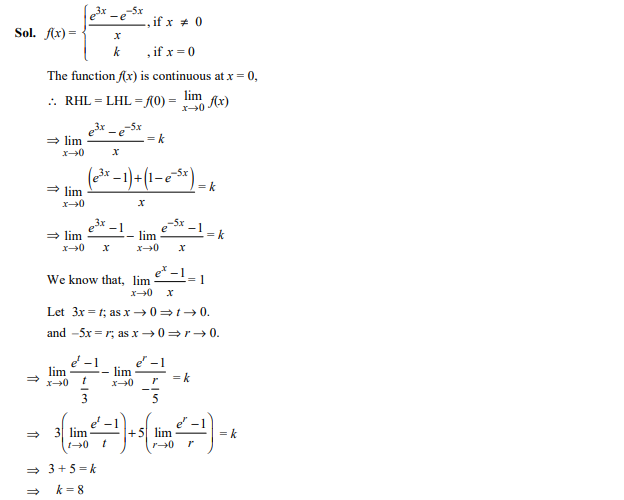
Question 13

If $C_{i j}$ denotes the cofactor of element $P_{i j}$ of the matrix P = $[\begin{matrix} 1 & - 1 & 2 \\ 0 & 2 & - 3 \\ 3 & 2 & 4 \end{matrix}]$ then the value of $C_{31}$ . $C_{23}$

5
24
$- 5$
$- 24$

Ans.(a)

Sol. Given, matrix is

P $= [\begin{matrix} 1 & - 1 & 2 \\ 0 & 2 & - 3 \\ 3 & 2 & 4 \end{matrix}]$

$C_{31} = {(- 1)}^{4} |\begin{matrix} - 1 & 2 \\ 2 & - 3 \end{matrix}| = 3 - 4 = - 1$

$C_{23} = {(- 1)}^{2 + 3} |\begin{matrix} - 1 & - 1 \\ 3 & 2 \end{matrix}| = - (2 + 3) = - 5$

Then, $C_{31} \cdot C_{23} = (- 1) \times (- 5) = 5$

Solutions

Question 14

The function is decreasing in the interval $y = x^{2} e^{- x}$ is decreasing in the interval

$(0, 2)$
$(2, \infty)$
$(- \infty, 0)$
$(- \infty, 0) \cup (2, \infty)$

Ans. (d)

Solutions

Question 15

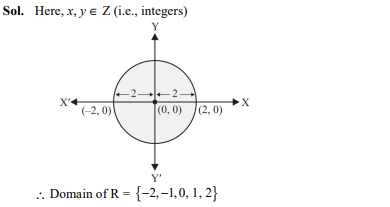
If R $= \{(x, y); x, y \in Z, x^{2} + y^{2} \leq 4\}$ is a relation in set Z, then domain of R is

{0, 1, 2}
{–2, –1, 0, 1, 2}
{0, –1, –2}
{–1, 0, 1}

Ans. (b)

Solutions

Question 16

The system of linear equations 5x + ky = 5, 3x + 3y = 5; will be consistent if

k $\neq$ – 3
k = – 5
k = 5
k $\neq$ 5

Ans. (d)

Sol.
The system of linear equation will be consistent if
$∆ \neq 0$
Now, $∆ = |\begin{matrix} 5 & k \\ 3 & 3 \end{matrix}| \neq 0 \Rightarrow 15 - 3 k \neq 0 \Rightarrow 3 k \neq 15 \Rightarrow k \neq 5$

Solutions

Question 17

The equation of the tangent to the curve $y (1 + x^{2}) = 2 - x,$ where it crosses the x-axis is

x – 5y = 2
5x – y = 2
x + 5y = 2
5x + y = 2

Ans. (c)

Solutions

Question 18

If $|\begin{matrix} 3 c + 6 & a - d \\ a + d & 2 - 3 b \end{matrix}| = [\begin{matrix} 12 & 2 \\ - 8 & - 4 \end{matrix}]$ are equal, then value of ab $-$ cd is

4
16
$-$ 6
$-$ 16

Ans. (a)

Solutions

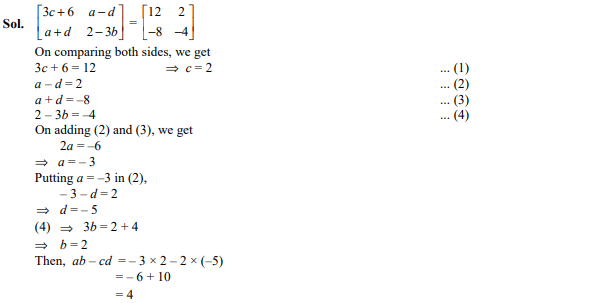
Question 19

The principal value of $\tan^{- 1} (\tan \frac{9 π}{8})$ is

$\frac{π}{8}$
$\frac{3 π}{8}$
$- \frac{π}{8}$
$- \frac{3 π}{8}$

Ans. (a)

Solutions

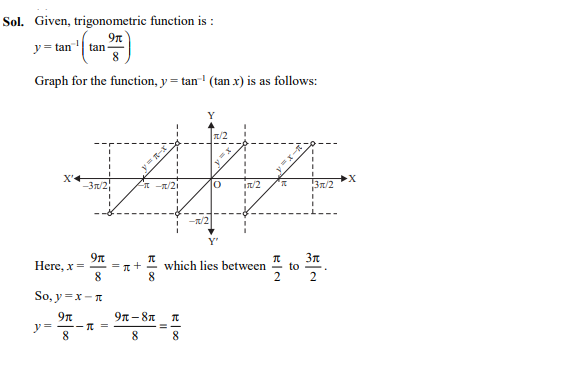
Question 20

For two matrices P = $[\begin{matrix} 3 & 4 \\ - 1 & 2 \\ 0 & 1 \end{matrix}]$ and $[\begin{matrix} - 1 & 2 & 1 \\ 1 & 2 & 3 \end{matrix}]$ , P $-$ Q is

$[\begin{matrix} 2 & 3 \\ - 3 & 0 \\ 0 & - 3 \end{matrix}]$
$[\begin{matrix} 4 & 3 \\ - 3 & 0 \\ - 1 & - 2 \end{matrix}]$
$[\begin{matrix} 4 & 3 \\ 0 & - 3 \\ - 1 & - 2 \end{matrix}]$
$[\begin{matrix} 2 & 3 \\ 0 & - 3 \\ 0 & - 3 \end{matrix}]$

Ans. (b)

Solutions

SECTION B

SECTION-B

(In this section, there are 20 questions. Any 16 are to be attempted).

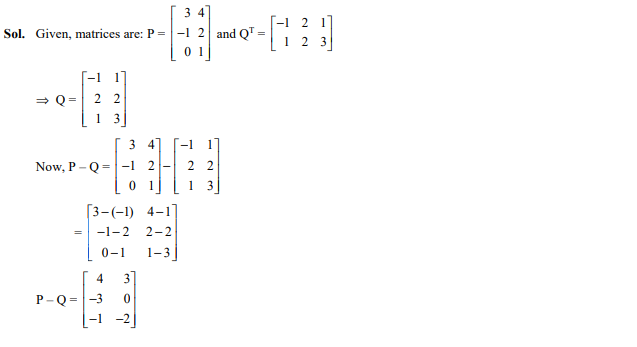
Question 21

The function $f (x) = 2 x^{3} - 15 x^{2} + 36 x + 6$ is increasing in the interval

$(- \infty, 2) \cup (3, \infty)$
$(- \infty, 2)$
$(- \infty, 2] \cup [3, \infty)$
$[3, \infty)$

Ans: (c);

Solutions

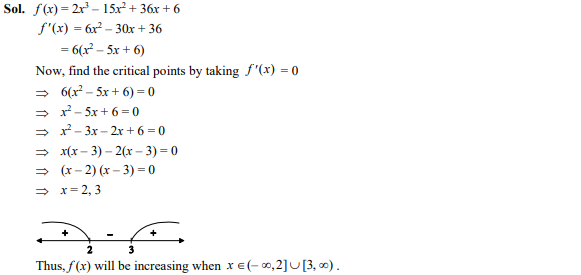
Question 22

If $x = 2 cosθ - \cos 2 θ and y = 2 sinθ - \sin 2 θ, then \frac{dy}{dx} is$

$\frac{\cos θ + \cos 2 θ}{\sin θ - \sin 2 θ}$
$\frac{\cos θ - \cos 2 θ}{\sin 2 θ - \sin θ}$
$\frac{\cos θ - \cos 2 θ}{\sin θ - \sin 2 θ}$
$\frac{\cos 2 θ - \cos θ}{\sin 2 θ - \sin θ}$

Ans. (b)

Solutions

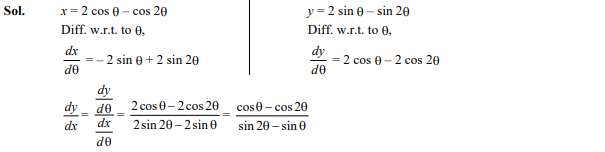
Question 23

What is the domain of the function $\cos^{- 1} (2 x - 3) ?$

$[- 1, 1]$
$(1, 2)$
$(- 1, 1)$
$[1, 2]$

Ans: (d);

Solutions

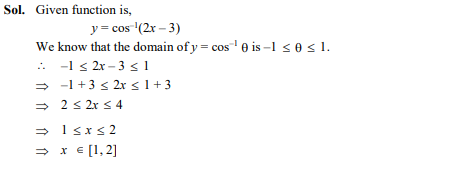
Question 24

Ans: (b);

Solutions

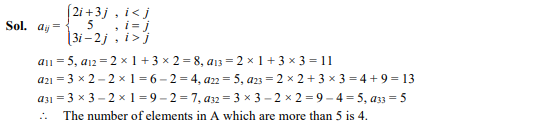
Question 25

If a function f defined by $f (x) = \{\begin{cases} \frac{kcosx}{π - 2 x}, & if x \neq \frac{π}{2} \\ 3, & if x = \frac{π}{2} \end{cases}$ , then the value of k is

2
3
6
$-$ 6

Ans. (c)

Solutions

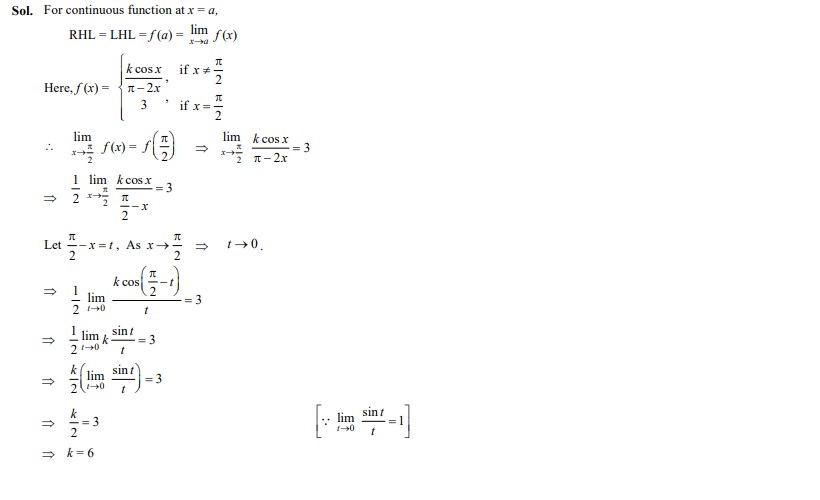
Question 26

For the matrix $X = [\begin{matrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \end{matrix}], (X^{2} - X)$ is

Ans. (a)

Solutions

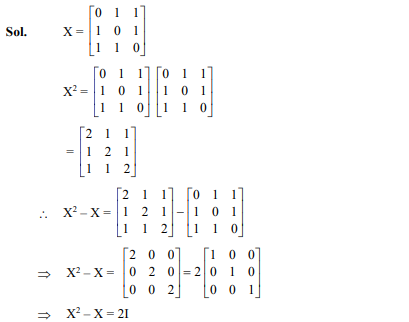
Question 27

Let $X = \{x^{2} : x \in N\}$ and the function $f : N \to X$ is defined by $f (x) = x^{2}, x \in N .$ Then this function is

injective only
not bijective
surjective only
bijective

Ans.(d)

Solutions

Question 28

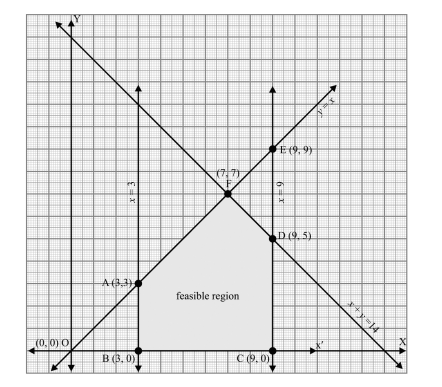
The corner points of the feasible region for a Linear Programming problem are P(0, 5), Q(1, 5), R(4, 2) and S(12, 0). The minimum value of the objective function Z = 2x + 5y is at the point

Sol. (c);

Given, points of the feasible region: P (0, 5), Q (1, 5), R (4, 2) and S (12, 0) and objective function Z = 2x + 5y

Here, $Z_{P} = 2 \times 0 + 5 \times 5 = 25$
$Z_{Q} = 2 \times 1 + 5 \times 5 = 27$
$Z_{R} = 2 \times 4 + 5 \times 2 = 18 \to M i n i m u m v a l u e$
$Z_{S} = 2 \times 12 + 5 \times 0 = 24$

Hence, the minimum value of Z is at the point R.

Solutions

Question 29

The equation of the normal to the curve $a y^{2} = x^{3}$ at the point $(a m^{2}, a m^{3}) i s$

$2 y - 3 m x + a m^{3} = 0$
$2 x + 3 m y - 3 a m^{4} - a m^{2} = 0$
$2 x + 3 m y + 3 a m^{4} - 2 a m^{2} = 0$
$2 x + 3 m y - 3 a m^{4} - 2 a m^{2} = 0$

Ans. (d)

Solutions

Question 30

If A is a square matrix of order 3 and $|A| = - 5$ ,then $|a d j A|$ is

125
–25
25
±25

Ans. (c)

Solutions

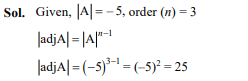
Question 31

The simplest form of $\tan^{- 1} [\frac{\sqrt{1 + x} - \sqrt{1 - x}}{\sqrt{1 + x} + \sqrt{1 - x}}]$

$\frac{π}{4} - \frac{π}{2}$
$\frac{π}{4} + \frac{π}{2}$
$\frac{π}{4} - \frac{1}{2} \cos^{- 1} x$
$\frac{π}{4} + \frac{1}{2} \cos^{- 1} x$

Ans.(c)

Solutions

Question 32

If for the matrix $A = |\begin{matrix} α & - 2 \\ - 2 & α \end{matrix}|, |A^{3}| = 125,$ then the value of $α$ is

$\pm 3$
$- 3$
$\pm 1$
$1$

Ans : (a);

Solutions

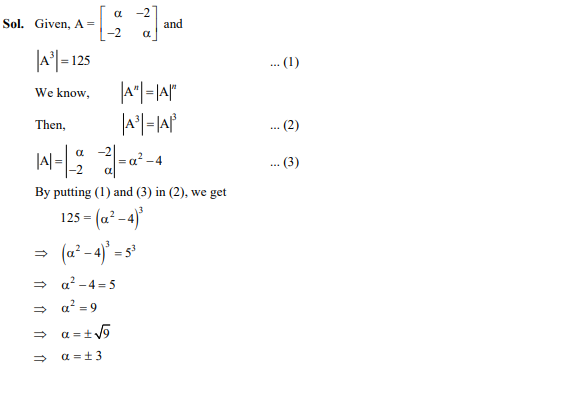
Question 33

If $y = \sin (m \sin^{- 1} x),$ then which one of the following equations is true?

$(1 - x^{2}) \frac{d^{2} y}{d x^{2}} + x \frac{d y}{d x} + m^{2} y = 0$
$(1 - x^{2}) \frac{d^{2} y}{d x^{2}} - x \frac{d y}{d x} + m^{2} y = 0$
$(1 + x^{2}) \frac{d^{2} y}{d x^{2}} - x \frac{d y}{d x} - m^{2} y = 0$
$(1 + x^{2}) \frac{d^{2} y}{d x^{2}} + x \frac{d y}{d x} - m^{2} x = 0$

Ans. (b)

Solutions

Question 34

The principal value of $[\tan^{- 1} \sqrt{3} - \cot^{- 1} (- \sqrt{3})]$ is

$π$
$- \frac{π}{2}$
0
$2 \sqrt{3}$

Ans. (b)

Solutions

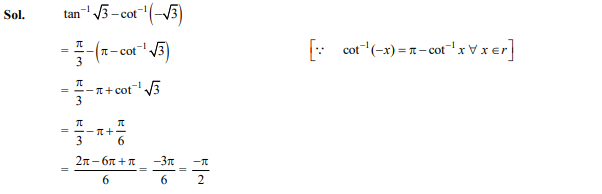
Question 35

The maximum value of ${(\frac{1}{x})}^{x}$ is

$e^{1 / e}$
$e$
${(\frac{1}{e})}^{1 / e}$
$e^{e}$

Ans. (a)

Solutions

Question 36

Let matrix $X = [x_{i j}]$ is given by $X = |\begin{matrix} 1 & 1 & - 2 \\ 3 & 4 & - 5 \\ 2 & 1 & - 3 \end{matrix}| .$ Then the matrix $Y = [m_{i j}]$ where $m_{i j}$ = Minor of $x_{i j}$ ,is

$[\begin{matrix} 7 & - 5 & - 3 \\ 19 & 1 & - 11 \\ - 11 & 1 & 7 \end{matrix}]$
$[\begin{matrix} 7 & - 19 & - 11 \\ 5 & - 1 & - 1 \\ 3 & 11 & 7 \end{matrix}]$
$[\begin{matrix} 7 & 19 & - 11 \\ - 3 & 11 & 7 \\ - 5 & - 1 & - 1 \end{matrix}]$
$[\begin{matrix} 7 & 19 & - 11 \\ - 1 & - 1 & 7 \\ - 3 & - 11 & 7 \end{matrix}]$

Ans. (d)

Solutions

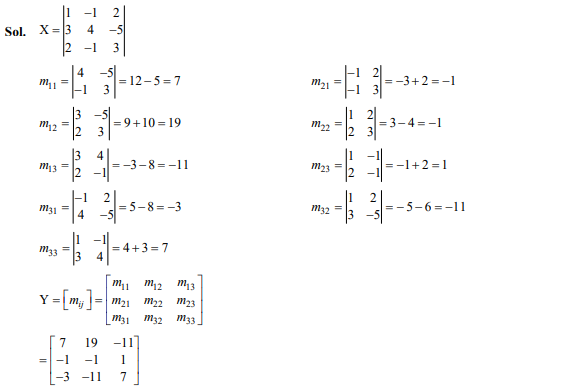
Question 37

A function $f : R \to R$ defined by $f (x) = 2 + x^{2} i s$

not one-one
one-one
not onto
neither one-one nor onto

Ans. (d)

Solutions

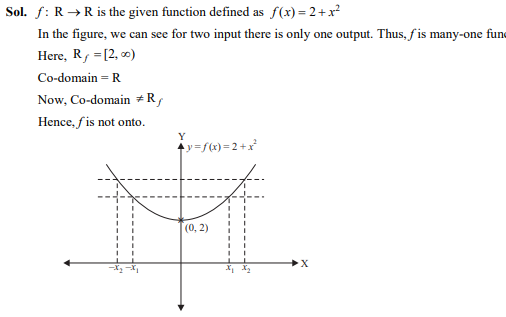
Question 38

Ans. (b)

Sol: Objective function Z = 2x – y + 5

Points of the feasible region are
A(0, 10), B(12, 6), C(20, 0) and O(0, 0)
$∴ Z_{A} = 2 \times 0 - 10 + 5 = - 5 — M i n . v a l u e Z_{B} = 2 \times 12 - 6 + 5 = 24 - 6 + 5 = 23 Z_{C} = 2 \times 20 - 0 + 5 = 40 + 5 = 45 Z_{O} = 0 - 0 + 5 = 5$

Solutions

Question 39

If x = – 4 is a root of $|\begin{matrix} x & 2 & 3 \\ 1 & x & 1 \\ 3 & 2 & x \end{matrix}| = 0,$ then the sum of the other two roots is

4
-3
2
5

Ans. (a)

Solutions

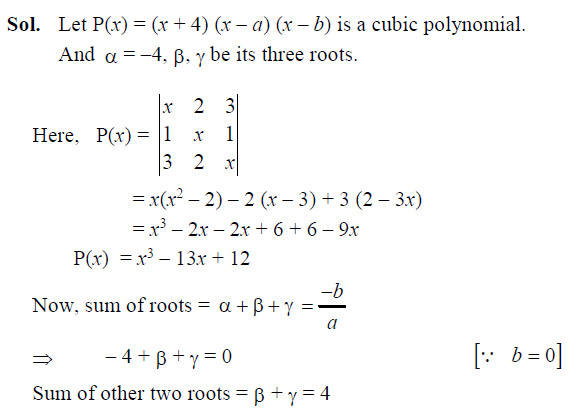
Question 40

The absolute maximum value of the function $f (x) = 4 x - \frac{1}{2} x^{2}$ in the interval $[2, \frac{9}{2}]$ is

Ans. (a)

Solutions

SECTION C

SECTION-C

(Attempt any 8 questions out of the Questions 41–50. Each question is of one mark).

Question 41

In a sphere of radius r, a right circular cone of height h having maximum curved surface area is inscribed. The expression for the square of curved surface of cone is

$2 π^{2} r h (2 r h + h^{2})$
$π^{2} h r (2 r h + h^{2})$
$2 π^{2} r (2 r h^{2} - h^{3})$
$2 π^{2} r^{2} (2 r h - h^{2})$

Ans. (c)

Solutions

Question 42

The corner points of the feasible region determined by a set of constraints (linear inequalities) are P(0, 5), Q(3, 5), R(5, 0) and S(4, 1) and the objective function is Z = ax + 2by where a, b > 0. The condition on a and b such that the maximum Z occurs at Q and S is

a – 5b = 0
a – 3b = 0
a – 2b = 0
a – 8b = 0

Ans. (d)

Solutions

Question 43

If curves $y^{2} = 4 x$ and xy = c cut at right angles, then the value of c is

$4 \sqrt{2}$
$8$
$2 \sqrt{2}$
$- 4 \sqrt{2}$

Ans. (a)

Solutions

Question 44

The inverse of the matrix $X = [\begin{matrix} 2 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 4 \end{matrix}]$ is

$24 [\begin{matrix} \frac{1}{2} & 0 & 0 \\ 0 & \frac{1}{3} & 0 \\ 0 & 0 & \frac{1}{4} \end{matrix}]$
$\frac{1}{24} [\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}]$
$\frac{1}{24} [\begin{matrix} 2 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 4 \end{matrix}]$
$[\begin{matrix} \frac{1}{2} & 0 & 0 \\ 0 & \frac{1}{3} & 0 \\ 0 & 0 & \frac{1}{4} \end{matrix}]$

Ans. (d)

Solutions

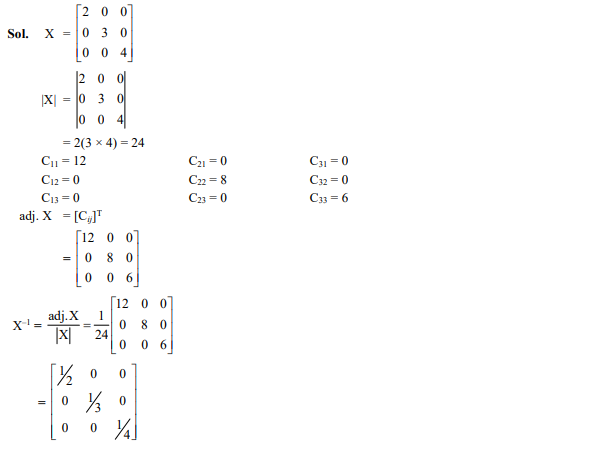
Question 45

For an L.P.P. the objective function is Z = 4x + 3y, and the feasible region determined by a set of constraints (linear inequations) is shown in the graph.

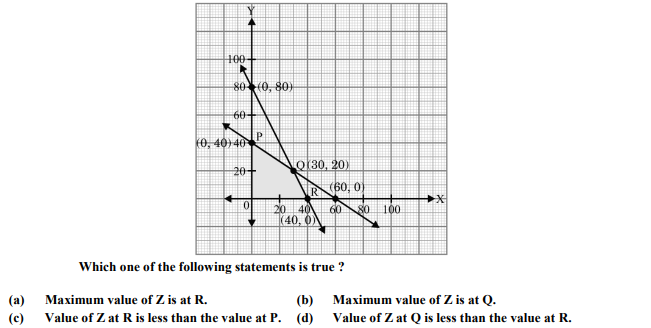
Ans. (b)

Sol. Z = 4x + 3y

Corner points of feasible region are P(0, 40), O(0, 0), R(40, 0), and Q(30, 20)
$Z_{P} = 4 \times 0 + 3 \times 40 = 120 Z_{O} = 0 Z_{R} = 4 \times 40 + 3 \times 0 = 160 Z_{Q} = 4 \times 30 + 3 \times 20 = 120 + 60 = 180 \leftarrow M a x i m u m v a l u e$

Solutions

Question 46

Let side of square plot is x m and its depth is h metres, then cost c for the pit is

$\frac{50}{h} + 400 h^{2}$
$\frac{12500}{h} + 400 h^{2}$
$\frac{250}{h} + h^{2}$
$\frac{250}{h} + 400 h^{2}$

Ans. (b)

Solutions

Question 47

Value of h (in m) for which $\frac{d c}{d h} = 0$ is

Ans. (c)

Solutions

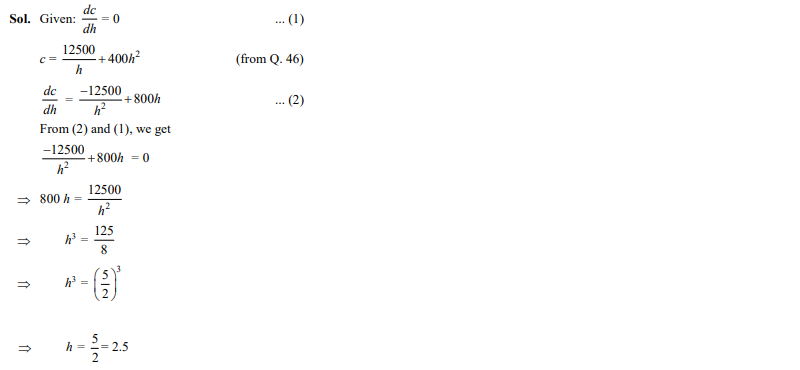
Question 48

$\frac{d^{2} c}{d h^{2}}$ is given by

$\frac{25000}{h^{3}} + 800$
$\frac{500}{h^{3}} + 800$
$\frac{100}{h^{3}} + 800$
$\frac{500}{h^{3}} + 2$

Ans. (a)

Solutions

Question 49

Value of x (in m) for minimum cost is

5
$10 \sqrt{\frac{5}{3}}$
$5 \sqrt{5}$
$10$

Ans. (d)

Solutions

Question 50

Total minimum cost of digging the pit (in ₹) is

4,100
7,500
7,850
3,220

Ans. (b)

Solutions

Board Paper of Class 12 2021 Mathematics Term-1 Set-4 CODE 065/2/4

General Instructions:

SECTION A

Question 1

Differential of log[log(logx5)] w.r.t.x is

Question 2

The number of all possible matrices of order 2 × 3 with each entry 1 or 2 is

Question 3

A function f : R → R is defined as f(x) = x 3 + 1 Then the function has

Question 4

If sin y = x cos (a + y), then dx dy is

Question 5

The points on the curve x29+y225=1, where tangent is parallel to x-axis are

Question 6

Three points P(2x, x + 3), Q(0, x) and R(x + 3, x + 6) are collinear, then x is equal to

Question 7

The principal value of cos-112+sin-1-12 is

Question 8

If (x2+y2)2 = xy then dydx is

Question 9

If a matrix A is both symmetric and skew symmetric, then A is necessarily a

Question 10

Let set X = {1, 2, 3} and a relation R is defined in X as : R = {(1, 3), (2, 2), (3, 2)}, then minimum ordered pairs which should be added in relation R to make it reflexive and symmetric are

Question 11

Question 12

The function f(x)={e3x-e-5xx,if x≠ 0 k ,if x= 0 is continuous at x = 0 for the value of k, as

Question 13

If Cij denotes the cofactor of element Pij of the matrix P = 1-1202-3324 then the value of C31 . C23

Question 14

The function is decreasing in the interval y = x2 e-x is decreasing in the interval

Question 15

If R =(x,y);x,y∈Z,x2+y2≤4 is a relation in set Z, then domain of R is

Question 16

The system of linear equations 5x + ky = 5, 3x + 3y = 5; will be consistent if

Question 17

The equation of the tangent to the curve y(1 + x2 ) = 2-x, where it crosses the x-axis is

Question 18

If 3c+6a-da+d2-3b=122-8-4 are equal, then value of ab-cd is

Question 19

The principal value of tan-1tan9π8 is

Question 20

For two matrices P = 34-1201 and -121123 , P-Q is

SECTION B

Question 21

The function f(x)=2x3-15x2+36x+6 is increasing in the interval

Question 22

If x=2cosθ-cos2θ and y=2sinθ-sin2θ, then dydx is

Question 23

What is the domain of the function cos-12x-3?

Question 24

Question 25

If a function f defined by f(x)=kcosxπ-2x,if x≠π23 ,if x=π2 , then the value of k is

Question 26

For the matrix X=011101110, X2-X is

Question 27

Let X=x2:x∈N and the function f: N→X is defined by fx=x2,x∈N. Then this function is

Question 28

The corner points of the feasible region for a Linear Programming problem are P(0, 5), Q(1, 5), R(4, 2) and S(12, 0). The minimum value of the objective function Z = 2x + 5y is at the point

Question 29

The equation of the normal to the curve ay2=x3 at the point (am2 , am3 ) is

Question 30

If A is a square matrix of order 3 and A = –5 ,then adj A is

Question 31

The simplest form of tan-11+x-1-x1+x+1-x

Question 32

If for the matrix A=α-2-2α, A3=125, then the value of α is

Question 33

If y = sin (m sin-1x), then which one of the following equations is true?

Question 34

The principal value of tan-13-cot-1-3 is

Question 35

The maximum value of 1xx is

Question 36

Let matrix X=xij is given by X=11-234-521-3. Then the matrix Y=mij where mij = Minor of xij ,is

Question 37

A function f:R→R defined by f(x) = 2 + x2 is

Question 38

Question 39

If x = – 4 is a root of x231x132x=0, then the sum of the other two roots is

Question 40

Differential of $\log [\log ({logx}^{5})] w . r . t . x$ is

A function $f : R \to R$ is defined as $f (x) = x^{3} + 1$ Then the function has

If $s i n y = x c o s (a + y),$ then $\frac{d x}{d y}$ is

The points on the curve $\frac{x^{2}}{9} + \frac{y^{2}}{25} = 1,$ where tangent is parallel to x-axis are

Three points $P (2 x, x + 3), Q (0, x) a n d R (x + 3, x + 6)$ are collinear, then x is equal to

The principal value of $\cos^{- 1} (\frac{1}{2}) + \sin^{- 1} (- \frac{1}{\sqrt{2}})$ is

If ${(x^{2} + y^{2})}^{2} = xy then \frac{dy}{dx} is$

The function $f (x) = {\begin{cases} \frac{e^{3 x} - e^{- 5 x}}{x}, if x \neq 0 \\ k, if x = 0 \end{cases}$ is continuous at x = 0 for the value of k, as

If $C_{i j}$ denotes the cofactor of element $P_{i j}$ of the matrix P = $[\begin{matrix} 1 & - 1 & 2 \\ 0 & 2 & - 3 \\ 3 & 2 & 4 \end{matrix}]$ then the value of $C_{31}$ . $C_{23}$

The function is decreasing in the interval $y = x^{2} e^{- x}$ is decreasing in the interval

If R $= \{(x, y); x, y \in Z, x^{2} + y^{2} \leq 4\}$ is a relation in set Z, then domain of R is

The equation of the tangent to the curve $y (1 + x^{2}) = 2 - x,$ where it crosses the x-axis is

If $|\begin{matrix} 3 c + 6 & a - d \\ a + d & 2 - 3 b \end{matrix}| = [\begin{matrix} 12 & 2 \\ - 8 & - 4 \end{matrix}]$ are equal, then value of ab $-$ cd is

The principal value of $\tan^{- 1} (\tan \frac{9 π}{8})$ is

For two matrices P = $[\begin{matrix} 3 & 4 \\ - 1 & 2 \\ 0 & 1 \end{matrix}]$ and $[\begin{matrix} - 1 & 2 & 1 \\ 1 & 2 & 3 \end{matrix}]$ , P $-$ Q is

The function $f (x) = 2 x^{3} - 15 x^{2} + 36 x + 6$ is increasing in the interval

If $x = 2 cosθ - \cos 2 θ and y = 2 sinθ - \sin 2 θ, then \frac{dy}{dx} is$

What is the domain of the function $\cos^{- 1} (2 x - 3) ?$

If a function f defined by $f (x) = \{\begin{cases} \frac{kcosx}{π - 2 x}, & if x \neq \frac{π}{2} \\ 3, & if x = \frac{π}{2} \end{cases}$ , then the value of k is

For the matrix $X = [\begin{matrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \end{matrix}], (X^{2} - X)$ is

Let $X = \{x^{2} : x \in N\}$ and the function $f : N \to X$ is defined by $f (x) = x^{2}, x \in N .$ Then this function is

The equation of the normal to the curve $a y^{2} = x^{3}$ at the point $(a m^{2}, a m^{3}) i s$

If A is a square matrix of order 3 and $|A| = - 5$ ,then $|a d j A|$ is

The simplest form of $\tan^{- 1} [\frac{\sqrt{1 + x} - \sqrt{1 - x}}{\sqrt{1 + x} + \sqrt{1 - x}}]$

If for the matrix $A = |\begin{matrix} α & - 2 \\ - 2 & α \end{matrix}|, |A^{3}| = 125,$ then the value of $α$ is

If $y = \sin (m \sin^{- 1} x),$ then which one of the following equations is true?

The principal value of $[\tan^{- 1} \sqrt{3} - \cot^{- 1} (- \sqrt{3})]$ is

The maximum value of ${(\frac{1}{x})}^{x}$ is

Let matrix $X = [x_{i j}]$ is given by $X = |\begin{matrix} 1 & 1 & - 2 \\ 3 & 4 & - 5 \\ 2 & 1 & - 3 \end{matrix}| .$ Then the matrix $Y = [m_{i j}]$ where $m_{i j}$ = Minor of $x_{i j}$ ,is

A function $f : R \to R$ defined by $f (x) = 2 + x^{2} i s$

If x = – 4 is a root of $|\begin{matrix} x & 2 & 3 \\ 1 & x & 1 \\ 3 & 2 & x \end{matrix}| = 0,$ then the sum of the other two roots is

The absolute maximum value of the function $f (x) = 4 x - \frac{1}{2} x^{2}$ in the interval $[2, \frac{9}{2}]$ is

If curves $y^{2} = 4 x$ and xy = c cut at right angles, then the value of c is

The inverse of the matrix $X = [\begin{matrix} 2 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 4 \end{matrix}]$ is

Value of h (in m) for which $\frac{d c}{d h} = 0$ is

$\frac{d^{2} c}{d h^{2}}$ is given by