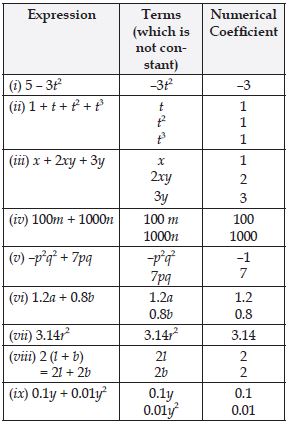
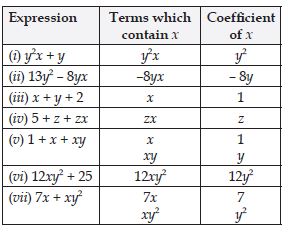
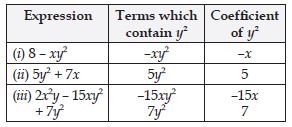
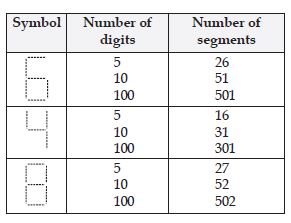
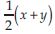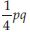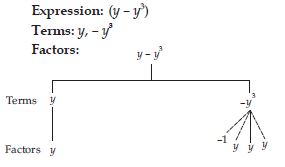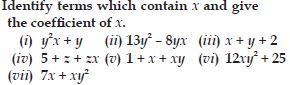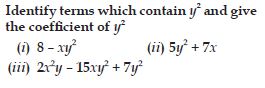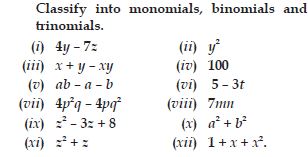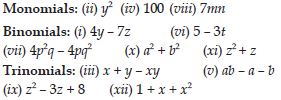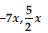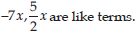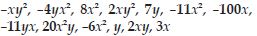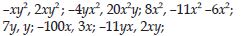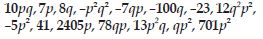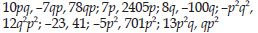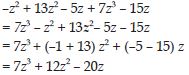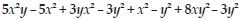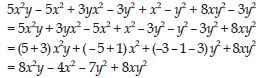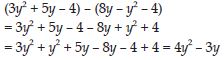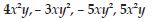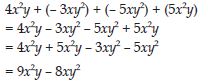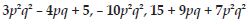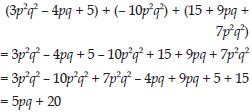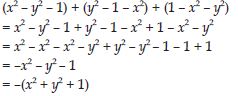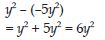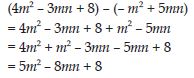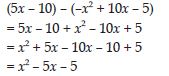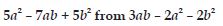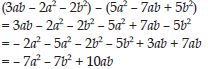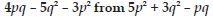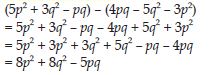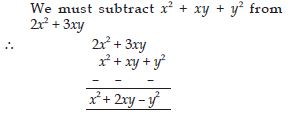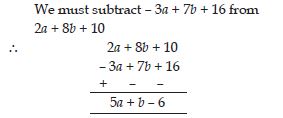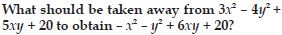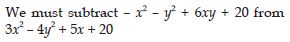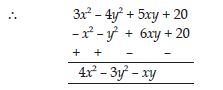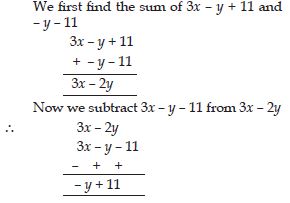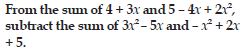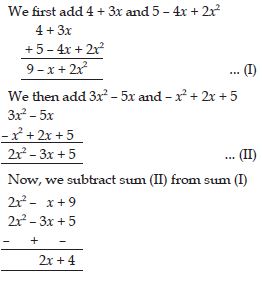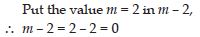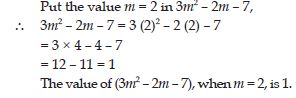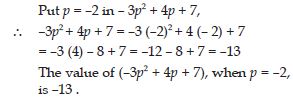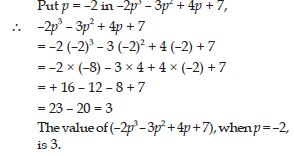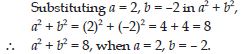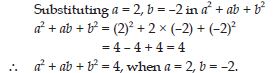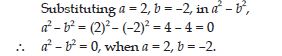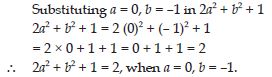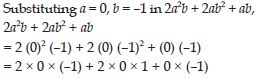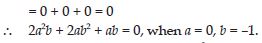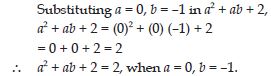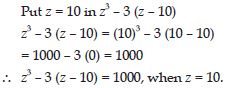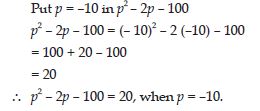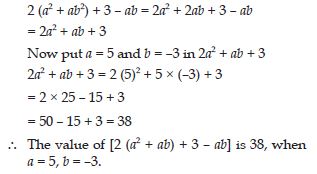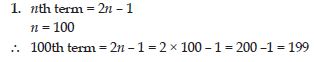Question 1:
Describe how the following expressions are obtained:
4x2 – 5x, 7xy + 5, x2y
Answer:
Question 2:
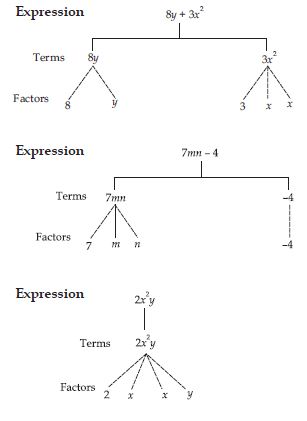
What are the terms in the following expressions? Show how the terms are formed. Draw a tree
diagram for each expression.
8y + 3x2, 7mn – 4, 2x2y.
Answer:
We can represent the terms and factors of the terms of an expression by a tree diagram
Question 3:
Write three expressions each having 4 terms.
Answer:
Three expressions each having 4 terms are:
(i) 4x2 – 3y2 + 9x – 8y
(ii) 4x2 – 3xy + 4x + 13
(iii) 5x3 – 5x2 – 5x – 5
Question 4:
Identify the coefficients in the following terms:
4x – 3y, a + b + 5, 2y + 5, 2xy.
Answer:
In 4x – 3y,
4 is the coefficient of x and – 3 is the coefficient
of y.
In a + b + 5
The coefficient of a and b is 1.
In 2y + 5, the coefficient of y is 2.
In 2xy, 2 is the coefficient of xy, x is the
coefficient of 2y and y is the coefficient of 2x.
Question 5:
Group the like terms together from the following:
12x, 12, –25x, –25, –25y, 1, x, 12y, y
Answer:
Like terms are:
(i) 12x, –25x, x
(ii) 12, –25, 1
(iii) –25y, 12y, y
Question 6:
Classify the following expressions as a monomial, a binomial or a trinomial:
a, a + b, ab + a + b, ab + a + b – 5, xy, xy + 5, 5x2 – x + 2, 4pq – 3q + 5p, 7,
4m – 7n + 10, 4mn + 7.
Answer:
Monomials: a, xy, 7
Binomials: a + b, xy + 5, 4mn + 7
Trinomials: ab + a + b, 5x2 – x + 2, 4m – 4n + 10,
4pq – 3q + 5p
Question 7:
Get the algebraic expression in the following cases using variables, constants and arithmatic
operations.
Subtraction of z from y.
Answer:
y – z
Question 8:
Get the algebraic expression in the following cases using variables, constants and arithmatic
operations.
One half of the sum of numbers x and y.
Answer:
Question 9:
Get the algebraic expression in the following cases using variables, constants and arithmatic
operations.
The number z multiplied by itself.
Answer:
z2
Question 10:
Get the algebraic expression in the following cases using variables, constants and arithmatic
operations.
One fourth of the product of numbers p and q.
Answer:
Question 11:
Get the algebraic expression in the following cases using variables, constants and arithmatic
operations.
Numbers x and y both squared and added.
Answer:
x2 + y2
Question 12:
Get the algebraic expression in the following cases using variables, constants and arithmatic
operations.
Number 5 added to three times the product of numbers m and n.
Answer:
3mn + 5
Question 13:
Get the algebraic expression in the following cases using variables, constants and arithmatic
operations.
Product of numbers y and z subtracted from 10.
Answer:
10 – yz
Question 14:
Get the algebraic expression in the following cases using variables, constants and arithmatic
operations.
Sum of numbers a and b subtracted from their product.
Answer:
ab – (a + b)
Question 15:
Identify the terms and their factors in the following expressions. Show the terms and factors
by tree diagrams.
x – 3
Answer:
Question 16:
Identify the terms and their factors in the following expressions. Show the terms and factors
by tree diagrams.
1 + x + x2
Answer:
Question 17:
Identify the terms and their factors in the following expressions. Show the terms and factors
by tree diagrams.
y – y3
Answer:
Question 18:
Identify the terms and their factors in the following expressions. Show the terms and factors
by tree diagrams.
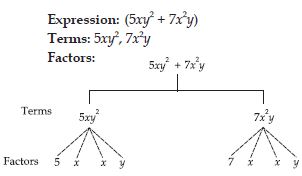
5xy2 + 7x2y
Answer:
Question 19:
Identify the terms and their factors in the following expressions. Show the terms and factors
by tree diagrams.
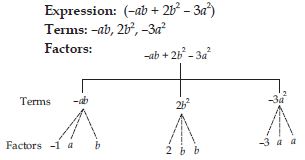
– ab + 2b2 – 3a2
Answer:
Question 20:
Answer:
Question 21:
Answer:
Question 22:
Answer:
Question 23:
Answer:
Question 24:
Answer:
Question 25:
State whether a given pair of terms is of like or unlike terms:
1, 100
Answer:
1, 100 are like terms.
Question 26:
State whether a given pair of terms is of like or unlike terms:
Answer:
Question 27:
State whether a given pair of terms is of like or unlike terms:
– 29x, – 29y
Answer:
–29x, –29y are unlike terms.
Question 28:
State whether a given pair of terms is of like or unlike terms:
14xy, 42yx
Answer:
14xy, 42yx are like terms.
Question 29:
State whether a given pair of terms is of like or unlike terms:
4m2p, 4mp2
Answer:
4m2p, 4mp2 are unlike terms.
Question 30:
State whether a given pair of terms is of like or unlike terms:
12xz, 12x2z2
Answer:
12xz, 12x2z2 are unlike terms.
Question 31:
Identify like terms in the following:
Answer:
Question 32:
Identify like terms in the following:
Answer:
Question 33:
Think of at least two situations in which you need to form two algebraic expressions and add or subtract them.
Answer:
(i) The sides of a triangle are x cm, y cm and z cm respectively. Then the perimeter of the
triangle is x + y + z.
(ii) Out of a class of 50 students, x students failed, then the number of students passed =
50 – x.
Question 34:
Add and subtract:
m – n, m + n
Answer:
m – n + m + n = 2m
m – n – (m + n) = m – n – m – n = – 2n
Question 35:
Add and subtract:
mn + 5 – 2, mn + 3
Answer:
(mn + 5 – 2) + (mn + 3) = mn + 5 – 2 + mn + 3
= 2mn + 6
(mn + 5 – 2) – (mn + 3) = mn + 5 – 2 – mn – 3 = 0
Question 36:
Simplify combining like terms:
21b – 32 + 7b – 20b
Answer:
21b – 32 + 7b – 20b
= 21b + 7b – 20b – 32 = (21 + 7 – 20) b – 32
= 8b – 32
Question 37:
Simplify combining like terms:
–z2 + 13z2 – 5z + 7z3 – 15z
Answer:
Question 38:
Simplify combining like terms:
p – (p – q) – q – (q – p)
Answer:
p – (p – q) – q – (q – p) = p – p + q – q – q + p
= p – p + p + q – q – q = p – q
Question 39:
Simplify combining like terms:
3a – 2b – ab – (a – b + ab) + 3ab + b – a
Answer:
3a – 2b – ab – (a – b + ab) + 3ab + b – a
= 3a – 2b – ab – a + b – ab + 3ab + b – a
= 3a – a – a – 2b + b + b – ab – ab + 3ab
= a + ab
Question 40:
Simplify combining like terms:
Answer:
Question 41:
Simplify combining like terms:
(3y2 + 5y2 – 4) – (8y – y2 – 4)
Answer:
Question 42:
Add:
3mn, – 5mn, 8mn, – 4mn
Answer:
(3mn) + (–5mn) + (8mn) + (–4mn)
= 3mn – 5mn + 8mn – 4mn
= 3mn + 8mn – 5mn – 4mn
= 11mn – 9mn = 2mn
Question 43:
Add:
t – 8tz, 3tz – z, z – t
Answer:
t – 8tz + 3tz – z + z – t
= t – t – 8tz + 3tz – z + z
= –5tz
Question 44:
Add:
–7mn + 5, 12mn + 2, 9mn – 8, – 2mn – 3
Answer:
(–7mn + 5) + (12mn + 2) + (9mn – 8) +
(–2mn – 3)
= –7mn + 5 + 12mn + 2 + 9mn – 8 – 2mn – 3
= –7mn + 12mn + 9mn – 2mn + 5 + 2 – 8 – 3
= 21mn – 9mn + 7 – 11 = 12mn – 4
Question 45:
Add:
a + b – 3, b – a + 3, a – b + 3
Answer:
(a + b – 3) + (b – a + 3) + (a – b + 3)
= a + b – 3 + b – a + 3 + a – b + 3
= a + b + b – a + a – b – 3 + 3 +3
= a + b + 3
Question 46:
Add:
14x + 10y – 12xy – 13, 18 – 7x – 10y
+ 8xy, 4xy
Answer:
(14x + 10y – 12xy – 13) +
(18 – 7x – 10y + 8xy) + 4xy
= 14x + 10y – 12xy – 13 + 18 – 7x – 10y + 8xy + 4xy
= (14 – 7)x + (10 – 10) y + (– 12 + 8 + 4) xy
+ (– 13 + 18) = 7x + 5
Question 47:
Add:
5m – 7n, 3n – 4m + 2, 2m – 3mn – 5
Answer:
(5m – 7n) + (3n – 4m + 2) + (2m – 3mn – 5)
= 5m – 7n + 3n – 4m + 2 + 2m – 3mn – 5
= 5m + 2m – 4m – 7n + 3n + 2 – 5 – 3mn
= 3m – 4n – 3 – 3mn
Question 48:
Add:
Answer:
Question 49:
Add:
Answer:
Question 50:
Add:
ab – 4a, 4b – ab, 4a – 4b
Answer:
(ab – 4a) + (4b – ab) + (4a – 4b)
= ab – 4a + 4b – ab + 4a – 4b
= ab – ab – 4a + 4a + 4b – 4b = 0
Question 51:
Add:
Answer:
Question 52:
Subtract:
–5y2 from y2
Answer:
Question 53:
Subtract:
6xy from – 12xy
Answer:
– 12xy – 6xy
= – 18xy
Question 54:
Subtract:
(a – b) from (a + b)
Answer:
(a + b) – (a – b)
= a + b – a + b = 2b
Question 55:
Subtract:
a(b – 5) from b(5 – a)
Answer:
b (5 – a) – a(b – 5)
= 5b – ab – ab + 5a
= 5a + 5b – 2ab
Question 56:
Subtract:
–m2 + 5mn from 4m2 – 3mn + 8
Answer:
Question 57:
Subtract:
–x2 + 10x – 5 from 5x – 10
Answer:
Question 58:
Subtract:
Answer:
Question 59:
Subtract:
Answer:
Question 60:
What should be added to x2 + xy + y2 to obtain 2x2 + 3xy?
Answer:
Question 61:
What should be subtracted from 2a + 8b + 10 to get – 3a + 7b + 16?
Answer:
Question 62:
Answer:
Question 63:
From the sum of 3x – y + 11 and – y – 11 subtract 3x – y – 11.
Answer:
Question 64:
Answer:
Question 65:
If m = 2, find the value of
m – 2
Answer:
The value of (m – 2), when m = 2, is 0.
Question 66:
If m = 2, find the value of
3m – 5
Answer:
Put the value m = 2 in 3m – 5,
∴ 3m – 5 = 3 (2) – 5 = 6 – 5 = 1
The value of (3m – 5), when m = 2, is 1.
Question 67:
If m = 2, find the value of
9 – 5m
Answer:
Put the value m = 2 in 9 – 5m,
∴ 9 – 5m = 9 – (5 × 2)
= 9 – 10 = – 1
The value of (9 – 5m), when m = 2, is – 1.
Question 68:
If m = 2, find the value of
3m2 – 2m – 7
Answer:
Question 69:
Answer:
Question 70:
If p = – 2, find the value of
4p + 7
Answer:
Put p = (–2) in 4p + 7,
∴ 4p + 7 = 4 × (– 2) + 7 = – 8 + 7 = – 1
The value of (4p + 7), when p = –2, is –1.
Question 71:
If p = – 2, find the value of
–3p2 + 4p + 7
Answer:
Question 72:
If p = – 2, find the value of
–2p3 – 3p2 + 4p + 7
Answer:
Question 73:
Find the value of the following expression,
when x = –1.
2x – 7
Answer:
Put x = –1 in 2x – 7,
2x – 7 = 2 (–1) – 7 = –2 – 7 = –9
∴ The value of (2x – 7), when x = –1, is –9.
Question 74:
Find the value of the following expression,
when x = –1.
–x + 2
Answer:
Put x = –1 in –x + 2,
–x + 2 = –(–1) + 2 = 1 + 2 = 3
The value of (–x + 2), when x = –1, is 3.
Question 75:
Find the value of the following expression,
when x = –1.
x2 + 2x + 1
Answer:
Put x = –1 in x2 + 2x + 1
x2 + 2x + 1 = (–1)2 + 2 (–1) + 1 = 1 – 2 + 1
= 2 – 2 = 0
The value of (x2 + 2x + 1), when x = –1, is 0.
Question 76:
Find the value of the following expression,
when x = –1.
2x2 – x – 2
Answer:
Put x = –1, in 2x2 – x – 2.
2x2 – x – 2 = 2 (–1)2 –(–1) – 2
= 2 × 1 + 1 – 2 = 2 + 1 – 2 = 3 – 2 = 1
The value of (2x2 – x – 2), when x = –1, is 1.
Question 77:
If a = 2, b = –2, find the value of:
a2 + b2
Answer:
Question 78:
If a = 2, b = –2, find the value of:
a2 + ab + b2
Answer:
Question 79:
If a = 2, b = –2, find the value of:
a2 – b2
Answer:
Question 80:
When a = 0, b = –1, find the value of the given
expressions:
2a + 2b
Answer:
Substituting a = 0, b = –1, in 2a + 2b,
2a + 2b = 2 (0) + 2 (–1)
= 0 – 2 = –2
∴ 2a + 2b = –2, when a = 0, b = –2.
Question 81:
When a = 0, b = –1, find the value of the given
expressions:
2a2 + b2 + 1
Answer:
Question 82:
When a = 0, b = –1, find the value of the given
expressions:
2a2b + 2ab2 + ab
Answer:
Question 83:
When a = 0, b = –1, find the value of the given
expressions:
a2 + ab + 2.
Answer:
Question 84:
Simplify the expressions and find the value
if x is equal to 2.
x + 7 + 4 (x – 5)
Answer:
Put x = 2 in the given expression,
x + 7 + 4 (x – 5) = x + 7 + 4x – 20
= 5x – 13
= 5 (2) – 13 = 10 – 13 = –3
∴ x + 7 + 4 (x – 5) = –3, when x = 2.
Question 85:
Simplify the expressions and find the value
if x is equal to 2.
3 (x + 2) + 5x – 7
Answer:
Put x = 2 in the given expression
3 (x + 2) + 5x – 7 = 3x + 6 + 5x – 7
= 8x – 1
= 8 × 2 – 1
= 16 – 1 = 15
∴ 3 (x + 2) + 5x – 7 = 15, when x = 2.
Question 86:
Simplify the expressions and find the value
if x is equal to 2.
6x + 5 (x – 2)
Answer:
Put x = 2 in the given expression.
6x + 5 (x – 2) = 6x + 5x – 10
= 11x – 10
= 11 (2) – 10 = 22 – 10 = 12
∴ 6x + 5 (x – 2) = 12, when x = 2.
Question 87:
Simplify the expressions and find the value
if x is equal to 2.
4 (2x – 1) + 3x + 11
Answer:
Put x = 2 in the given expression.
4 (2x – 1) + 3x + 11 = 8x – 4 + 3x + 11
= 11x + 7
= 11 × 2 + 7 = 22 + 7 = 29
∴ 4 (2x – 1) + 3x + 11 = 29, when x = 2.
Question 88:
Simplify these expressions and find their
value if x = 3, a = –1, b = –2.
3x – 5 – x + 9
Answer:
3x – 5 – x + 9 = 3x – x – 5 + 9 = 2x + 4
Now, put x = 3 in 2x + 4,
2x + 4 = 2 × 3 + 4 = 6 + 4 = 10
∴ 3x – 5 – x + 9 = 10, when x = 3.
Question 89:
Simplify these expressions and find their
value if x = 3, a = –1, b = –2.
2 – 8x + 4x + 4
Answer:
2 – 8x + 4x + 4 = 2 + 4 – 8x + 4x
= 6 – 4x
Now, put x = 3 in 6 – 4x
6 – 4x = 6 – 4 × 3 = 6 – 12 = –6
∴ 2 – 8x + 4x + 4 = – 6, when x = 3.
Question 90:
Simplify these expressions and find their
value if x = 3, a = –1, b = –2.
3a + 5 – 8a + 1
Answer:
3a + 5 – 8a + 1 = 3a – 8a + 5 + 1
= –5a + 6
Now, put a = – 1 in – 5a + 6,
– 5a + 6 = – 5 (– 1) + 6 = 5 + 6 = 11
∴ 3a + 5 – 8a + 1 = 11, when a = – 1.
Question 91:
Simplify these expressions and find their
value if x = 3, a = –1, b = –2.
10 – 3b – 4 – 5b
Answer:
10 – 3b – 4 – 5b = 10 – 4 – 3b – 5b = 6 – 8b
Now, put b = –2 in 6 – 8b
6 – 8b = 6 – 8 × (–2) = 6 + 16 = 22
∴ 10 – 3b – 4 – 5b = 22, when b = –2.
Question 92:
Simplify these expressions and find their
value if x = 3, a = –1, b = –2.
2a – 2b – 4 – 5 + a
Answer:
2a – 2 b – 4 – 5 + a = 2 a + a – 2 b – 4 – 5
= 3a – 2b – 9
Now, put a = –1, b = –2 in 3a – 2b – 9,
3a – 2b – 9 = 3 (– 1) – 2 (–2) – 9 = – 3 + 4 – 9
= –12 + 4 = –8
∴ 2a – 2b – 4 – 5 + a = – 8, when a = –1, b = –2.
Question 93:
If z = 10, find the value of z3 – 3 (z – 10).
Answer:
Question 94:
If p = –10, find the value of p2 – 2p – 100.
Answer:
Question 95:
What should be the value of a if the value of 2x2 + x – a equals to 5, when x = 0 ?
Answer:
Here, 2x2 + x – a = 5
Putting x = 0, we get
2 (0)2 + (0) – a = 5
–a = 5
∴ a = –5
Question 96:
Simplify the expression and find its value
when a = 5 and b = –3.
2 (a2 + ab) + 3 – ab.
Answer:
Question 97:
Answer:
Question 98:
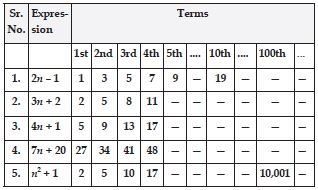
Use the given algebraic expression to complete the table of number patterns (sequences).