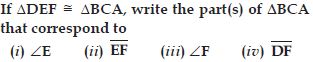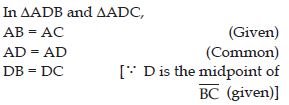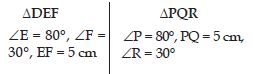Question 1:
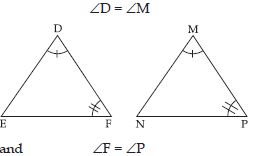
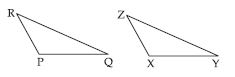
When two triangles, say ABC and PQR are
given, there are, in all, six possible matchings
or correspondences. Two of them are
(i) ABC PQR and (ii) ABCQRP.
Find the other four correspondences by
using two cutouts of triangles. Will all these
correspondences lead to congruence? Think
about it.
Answer:
Other four correspondences are:
ABCPRQ , ABCQPR
ABCRPQ , ABCRQP
All these correspondences will not lead to congruence.
If in any one of thse correspondences, the two triangles
coincide then we say that the two triangles are
congruent.
Question 2:
Two line segments are congruent if ___________ .
Answer:
they have the same length.
Question 3:
Among two congruent angles, one has a measure of 70; the measure of the other angle is ____________ .
Answer:
70
Question 4:
When we write A = B we actually mean ____________.
Answer:
mA = mB.
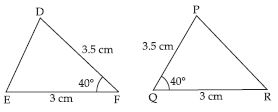
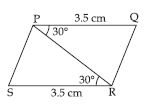
Question 5:
Give any two real-life examples for congruent shapes.
Answer:
(i) Take two stamps of same denomination.
Place one stamp over the other. We observe
that one stamp covers the other completely
and exactly. This means that the stamps are
of the same shape and same size.
So, two stamps used are congruent to one
another.
(ii) Take two blades of the same brand. When we place one blade over the other; we observe
that one blade covers the other blade exactly. So; two blades are congruent to one another.
Question 6:
If ABC FED under the correspondence ABC FED, write all the corresponding congruent parts of the triangles.
Answer:
If ABC FED under the correspondence
ABCFED it follows that congruent parts
(i.e., the matching parts) of congruent triangles
are equal.
Therefore all the corresponding congruent parts
of the triangles are:
AB = FE, BC = ED and AC = FD
A = F, B = E and C = D
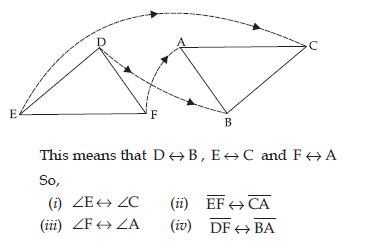
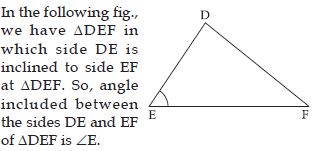
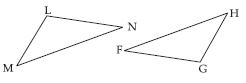
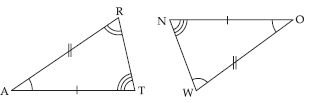
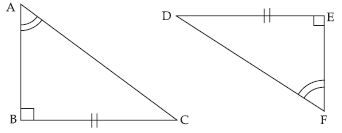
Question 7:
Answer:
DEF BCA. Therefore the correspondence
is DEFBCA.
For better understanding of the correspondence let us use a diagram.
Question 8:
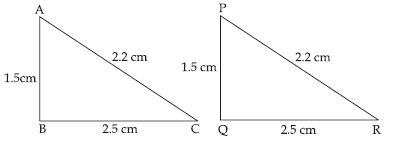
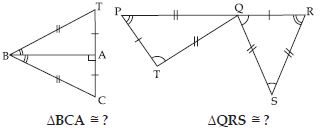
In fig., lengths of the sides of the triangles are indicated. By applying the SSS congruence rule, state which pairs of triangles are congruent. In case of congruent triangles, write the result in symbolic form:
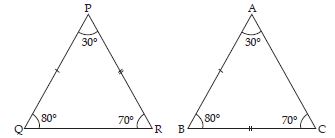
Answer:
In ABC and PQR, we have;
AB = PQ (= 1.5), BC = QR (= 2.5) and
AC = PR = 2.2
This shows that the three sides of ABC
are equal to the three sides of PQR.
So, by SSS congruence rule two triangles
are congruent.
The correspondence is AP , BQ
and CR.
So, in symbolic form ABC PQR
Question 9:
In fig., lengths of the sides of the triangles are indicated. By applying the SSS congruence rule, state which pairs of triangles are congruent. In case of congruent triangles, write the result in symbolic form:
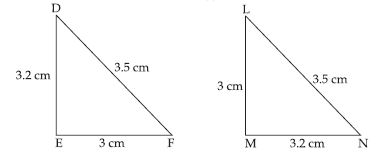
Answer:
In DEF and LMN, we have;
DE = MN (= 3.2), EF = LM (= 3) and DF = LN
(= 3.5)
This shows that the three sides of DEF
are equal to the three sides of LMN.
So, by SSS congruence rule two triangles
are congruent.
The correspondence is DN, EM
and FL.
So, in symbolic form
DEF NML
Question 10:
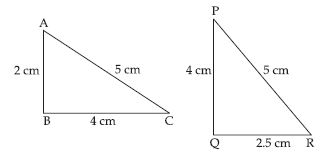
In fig., lengths of the sides of the triangles are indicated. By applying the SSS congruence rule, state which pairs of triangles are congruent. In case of congruent triangles, write the result in symbolic form:
Answer:
In ABC and PQR, we have
BC = PR (= 4), AC = PQ (= 5)
But AB QR [ 2 2.5]
So, SSS congruence rule does not
applicable.
Therefore ABC is not congruent to PQR.
Question 11:
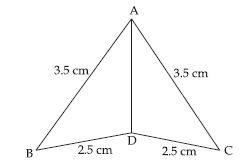
In fig., lengths of the sides of the triangles are indicated. By applying the SSS congruence rule, state which pairs of triangles are congruent. In case of congruent triangles, write the result in symbolic form:
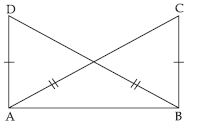
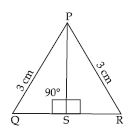
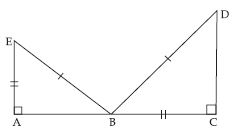
Answer:
In ABC and ADC, we have
AB = AC (= 3.5), BD = DC (= 2.5) and AD = AD
This shows that the three sides of ABD
are equal to the three sides of ADC.
So, by SSS congruence rule two triangles
are congruent.
The correspondence is AA , BC
and DD.
So; in symbolic form
ABD ACD
Question 12:
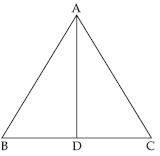
State the three pairs of equal parts in ADB and ADC.
Answer:
Question 13:
Is ADB ADC? Give reasons.
Answer:
Yes; ADB ADC.
Reason: In ADB and ADC,
AB = AC (Given)
AD = AD (Common)
DB = DC [ D is the midpoint of BC (given)]
We observe that three sides of ADB are equal to the three sides of ADB are equal to the three sides of
ADC.
So, by SSS congruence rule two triangles are congruent.
The congrunece is AA , DD and BC
So, ADB ADC
Question 14:
Is B = C? Why?
Answer:
Yes; B = C
Reason: In ADB and ADC,
AB = AC (Given)
AD = AD (Common)
DB = DC [ D is the midpoint of BC (given)]
We observe that three sides of ADB are equal to the three sides of ADB are equal to the three sides of
ADC.
So, by SSS congruence rule two triangles are congruent.
The congrunece is AA , DD and BC
So, ADB ADC
Thus B corresponds to C (i.e. BC ) corresponding parts of congruent triangles are equal.
B = C
Question 15:
In fig., AC = BC and AD = BC. Which of the following statements is meaningfully written?
(i) ABC ABD
(ii) ABC BAD.
Answer:
In ABC and ABD,
AC = BD (given)
AD = BC (given)
and AB = AB (common)
This shows that the three sides of ABC are equal to the three sides of ABD.
So, by SSS congruence rule two triangles are congruent.
The correspondence is AB , BA and CD .
So in symbolic form, ABC BAD
Hence, statement (ii) i.e., ABC BAD is meaningfully written.
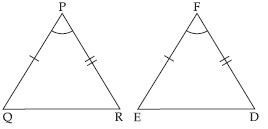
Question 16:
Draw two isosceles triangle ABC with AB = AC.
State the three pairs of equal parts in ABC and ACB.
Answer:
Three pairs of equal parts in ABC and ACB are as follows:
In ABC and ACB,
AB = AC (given)
BC = CB (same side of both triangles)
AC = AB (given)
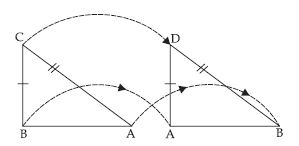
Question 17:
Draw two isosceles triangle ABC with AB = AC.
Is ABC ACB? Why or why not?
Answer:
Yes; ABC ACB by SSS congruence
In ABC and ACB,
AB = AC (given)
BC = CB (same side of both triangles)
AC = AB (given)
Therefore, ABC ACB by SSS congruence
Question 18:
Draw two isosceles triangle ABC with AB = AC.
Is B = C? Why or why not?
Answer:
Yes; B = C
In ABC and ACB,
AB = AC (given)
BC = CB (same side of both triangles)
AC = AB (given)
Therefore, ABC ACB by SSS congruence
B = C
[Congruent parts of congruent triangles.]
Question 19:
Answer:
Question 20:
By applying SAS congruence rule, you want to establish that PQR FED. It is given that PQ = FE and RP = DF. What additional information is needed to establish the congruence?
Answer:
In PQR and FED; we are given equality of two
corresponding sides as PQ = FE and RP = DF.
To establish PQR FED under SAS
congruence we need the equality.
Angles included between the sides PQ and RR,
FE and DF.
So, included P should be equal to included F.
Question 21:
In fig., measures of some parts of the triangles are indicated. By applying SAS congruence rule, state the pairs of congruent triangles, if any, in each case. In case of congruent triangles, write them in symbolic form.
Answer:
In ABC and DEF, we have
AB = DE (= 2.5 cm) and AC = DF (= 2.8 cm)
but included A included D
[ A = 80 and D = 70 and 80 70]
So, SAS congruence rule does not
applicable.
Therefore ABC is not congruent to DEF.
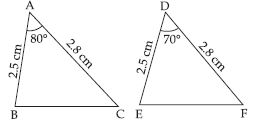
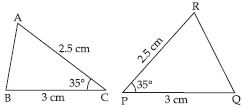
Question 22:
In fig., measures of some parts of the triangles are indicated. By applying SAS congruence rule, state the pairs of congruent triangles, if any, in each case. In case of congruent triangles, write them in symbolic form.
Answer:
In ABC and RPQ, we have ;
AC = RP (= 2.5 cm), BC = PQ (= 3 cm)
and included C = included P (= 35)
So, by SAS congruence rule two triangles
are congruent.
The correspondence is
AR , CP and B Q
So, in symbolic form ABC RQP.
Question 23:
In fig., measures of some parts of the triangles are indicated. By applying SAS congruence rule, state the pairs of congruent triangles, if any, in each case. In case of congruent triangles, write them in symbolic form.
Answer:
DEF and PQR
EF = QR (= 3 cm) and DF = PR (= 3.5 cm)
But included F included R
[ F = 40 given but measure of R is not
given as 40]
So, SAS congruence rule does not
applicable.
Therefore DEF is not congruent to PQR.
Question 24:
In fig., measures of some parts of the triangles are indicated. By applying SAS congruence rule, state the pairs of congruent triangles, if any, in each case. In case of congruent triangles, write them in symbolic form.
Answer:
In fig. PQRS is a parallelogram. Diagonal
PR divides it into two triangles PQR and
PRS.
Now, in PQR and PRS, we have
PQ = SR (= 3.5 cm) PR = PR (common)
and included P = included R (= 30).
So, by SAS congruence rule two triangles
are congruent.
The correspondence is
PR , Q S , RP
So, in symbolic form PQR RSP.
Question 25:
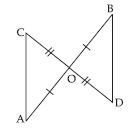
State the three pairs of equal parts in two triangles AOC and BOD.
Answer:
Question 26:
Which of the following statements are true?
(a) AOC DOB
(b) AOC BOD
Answer:
In AOC and BOD
AO = OB,
OC = OD and
included AOC = included BOD.
This shows that by SAS congruence rule two triangles are congruent.
The correspondence is AB , OO , CD
So in symbolic form AOC BOD
Hence, statement (b) i.e. AOC BOD is true.
Question 27:
What is the side included between the angles
M and N of MNP?
Answer:
The side included between the angles M and N of MNP are MN.
Question 28:
You want to establish DEF MNP, using the ASA congruence rule. You are given that D = M and F = P. What information is needed to establish the congruence? (Draw a rough figure and then try !)
Answer:
We want to establish DEF MNP, using the ASA congruence rule for this, we have given
Also, required included sides are DF = MP
Question 29:
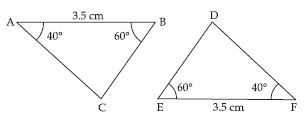
In fig., measures of some parts are indicated.
By applying ASA congruence rule, state which
pairs of triangles are congruent. In case of
congruence, write the result in symbolic form.
Answer:
Yes, ABC DEF
Reason: In ABC and FED,
A = F = 40
AB = EF = 3.5 cm
B = E = 60
By ASA congruence rule,
ABC FED
Question 30:
In fig., measures of some parts are indicated.
By applying ASA congruence rule, state which
pairs of triangles are congruent. In case of
congruence, write the result in symbolic form.
Answer:
No, given triangles are not congruent.
Question 31:
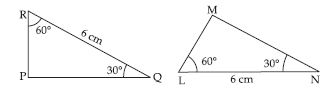
In fig., measures of some parts are indicated.
By applying ASA congruence rule, state which
pairs of triangles are congruent. In case of
congruence, write the result in symbolic form.
Answer:
Yes, PRQ MLN
Reason: In RPQ and LMN,
R = L = 90
RQ = LN = 6 cm
Q = N = 30
By ASA congruence rule,
RPQ LMN
Question 32:
In fig., measures of some parts are indicated.
By applying ASA congruence rule, state which
pairs of triangles are congruent. In case of
congruence, write the result in symbolic form.
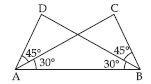
Answer:
Yes, DAB CAB,
Reason: In DAB and CBA
DAB = CBA = 45 + 30 = 75
AB = BA (Common side)
DBA = CAB = 30
By ASA congruence rule,
DAB CAB
Question 33:
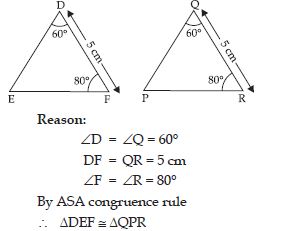
Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by ASA congruence rule. In case of congruence, write it in symbolic form.
Answer:
Yes, DEF PQR
Question 34:
Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by ASA congruence rule. In case of congruence, write it in symbolic form.
Answer:
No, DEF is not congruent to PQR.
Question 35:
Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by ASA congruence rule. In case of congruence, write it in symbolic form.
Answer:
No, DEF is not congruent to PQR.
Question 36:
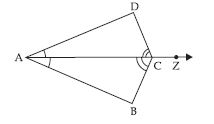
In fig., ray AZ bisects DAB as well as DCB.
State the three pairs of equal parts in triangles BAC and DAC.
Answer:
Three pairs of equal parts in triangles BAC and DAC are:
BAC = DAC [ AZ bisects DAB]
BCA = DCA [ AZ bisects DCB]
AC = CA (Common side)
Question 37:
In fig., ray AZ bisects DAB as well as DCB.
Is BAC DAC? Give reasons.
Answer:
In BAC and DAC
BAC = DAC [ AZ bisects DAB]
BCA = DCA [ AZ bisects DCB]
AC = CA (Common side)
By ASA congruence rule,
BAC DAC
Question 38:
In fig., ray AZ bisects DAB as well as DCB.
Is AB = AD? Justify your answer.
Answer:
Yes, AB = AD
Reason:
In BAC and DAC
BAC = DAC [ AZ bisects DAB]
BCA = DCA [ AZ bisects DCB]
AC = CA (Common side)
By ASA congruence rule,
BAC DAC
AB = AD (CPCT)
Question 39:
In fig., ray AZ bisects DAB as well as DCB.
Is CD = CB? Give reasons.
Answer:
Yes, CD = CB
Reason:
In BAC and DAC
BAC = DAC [ AZ bisects DAB]
BCA = DCA [ AZ bisects DCB]
AC = CA (Common side)
By ASA congruence rule,
BAC DAC
CD = CB (CPCT)
Question 40:
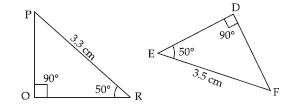
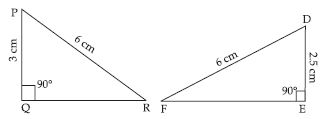
In fig, measures of some parts of triangles are given. By applying RHS congruence rule, state which pairs of triangles are congruent. In case of congruent triangles, write the result in symbolic form.
Answer:
No, PQR is not congruent to DEF.
Yes, CAB DAB
Reason:
C = D = 90
AB = AB = 3.5 cm
CA = DB = 2 cm
By RHS congruence rule,
CAB DAB
Question 41:
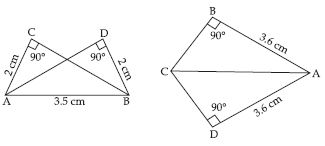
In fig, measures of some parts of triangles are given. By applying RHS congruence rule, state which pairs of triangles are congruent. In case of congruent triangles, write the result in symbolic form.
Answer:
Yes, ABC ADC
Reason:
B = D = 90
CA = CA (Common side)
BA = DA = 3.6 cm
By RHS congruence rule,
ABC ADC
Question 42:
In fig, measures of some parts of triangles are given. By applying RHS congruence rule, state which pairs of triangles are congruent. In case of congruent triangles, write the result in symbolic form.
Answer:
Yes, PSQ PSR
Reason:
PSQ = PSR = 90
PQ = PR = 3 cm
PS = PS (Common side)
By RHS congruence rule,
PSQ PSR
Question 43:
It is to be established by RHS congruence rule that ABC RPQ. What additional information is needed, if it is given that: B = P = 90 and AB = RP?
Answer:
Question 44:
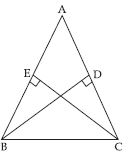
In fig., BD and CE are altitudes of ABC such that BD = CE.
State the three pairs of equal parts in CBD and BCE.
Answer:
Three pairs of equal parts in CBD and BCE are:
D = E = 90
CB = BC (Common side)
BD = CE (Given)
Question 45:
In fig., BD and CE are altitudes of ABC such
that BD = CE.
Is CBD BCE? Why or why not?
Answer:
Yes, CBD BCE.
Reason:
In CBD and BCE
D = E = 90
CB = BC (Common side)
BD = CE (Given)
By RHS Congruence rule,
CBD BCE
Question 46:
In fig., BD and CE are altitudes of ABC such
that BD = CE.
Is DCB = EBC? Why or why not?
Answer:
Yes, DCB EBC
Reason:
In CBD and BCE
D = E = 90
CB = BC (Common side)
BD = CE (Given)
By RHS Congruence rule,
CBD BCE
DCB = EBC (CPCT)
Question 47:
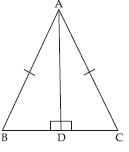
ABC is an isosceles triangle with AB = AC and AD is one of its altitudes (fig.).
State the three pairs of equal parts in ADB and ADC.
Answer:
Three pairs of equal parts in ADB and ADC are:
ADB = ADC = 90
AB = AC (Given)
AD = AD (Common side)
Question 48:
ABC is an isosceles triangle with AB = AC and AD is one of its altitudes (fig.).
Is ADB ADC? Why or why not?
Answer:
Yes, ADB ADC
Reason:
In ADB and ADC
ADB = ADC = 90
AB = AC (Given)
AD = AD (Common side)
By RHS Congruence rule,
ADB ADC
Question 49:
ABC is an isosceles triangle with AB = AC
and AD is one of its altitudes (fig.).
Is B = C? Why or why not?
Answer:
Yes, B = C
Reason:
In ADB and ADC
ADB = ADC = 90
AB = AC (Given)
AD = AD (Common side)
By RHS Congruence rule,
ADB ADC
B = C (CPCT)
Question 50:
ABC is an isosceles triangle with AB = AC and AD is one of its altitudes (fig.).
Is BD = CD? Why or why not?
Answer:
Yes, BD CD
Reason:
In ADB and ADC
ADB = ADC = 90
AB = AC (Given)
AD = AD (Common side)
By RHS Congruence rule,
ADB ADC
BD = CD (CPCT)
Question 51:
Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ABC DEF
Answer:
In ABC and DEF,
Given that,
AC = DF
AB = DE
and BC = EF
So, ABC DEF
By SSS congruence criterion.
Question 52:
Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
PRQ = XZY
So, PQR XYZ
Answer:
In RPQ and ZXY,
Given that,
RP = ZX
RQ = ZY
and PRQ = XZY
So, PQR XYZ
By SAS congruence criterion.
Question 53:
Which congruence criterion do you use in the following?
Given: MLN = FGH
NML = GFH
ML = FG
So, LMN GFH
Answer:
In LMN and GFH,
Given that,
MLN = FGH
NML = GFH
ML = FG
So, LMN GFH
By ASA congruence criterion.
Question 54:
Which congruence criterion do you use in the following?
Given: EB = DB
AE = BC
A = C = 90
So, ABE CDB
Answer:
In ABE and CDB,
Given that,
EB = DB
AE = BC
A = C = 90
So, ABE CDB
By RHS congruence criterion.
Question 55:
You want to show that ART PEN,
If you have to use SSS criterion, then you need to show
(i) AR = (ii) RT = (iii) AT =
Answer:
ART PEN (Given)
By SSS criterion, then
(i) AR = PE
(ii) RT = EN
(iii) AT = PN
Question 56:
You want to show that ART PEN,
If it is given that T = N and you are to use SAS criterion, you need to have
(i) RT = and (ii) PN =
Answer:
ART PEN [Given]
and T = N
Using SAS criterion, then
(i) RT = EN
(ii) PN = AT
Question 57:
You want to show that ART PEN,
If it is given that AT = PN and you are to use ASA criterion, you need to have:
(i) ? (ii) ?
Answer:
ART PEN (Given)
By using ASA criterion,
Also, AT = PN (Given)
(i) RAT = EPN
(ii) ATR = PNE
Question 58:
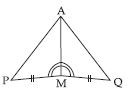
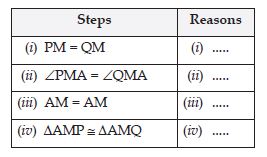
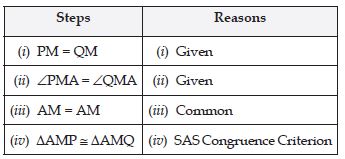
You have to show that AMP AMQ. In the
following proof, supply the missing reasons.
Answer:
Question 59:
In ABC, A = 30, B = 40 and C = 110
In PQR, P = 30, Q = 40 and R = 110
A student says that ABC PQR by AAA congruence criterion. Is he justified? Why or why not?
Answer:
No, AAA congruence criterion is not sufficient to say that two triangles are congruent because angle shows the direction (or inclination) of any triangle and not its size.
Question 60:
In the figure, the two triangles are congruent. The corresponding parts are marked. We can write RAT ?
Answer:
Given that, AT = ON
AR = OW
A = O
R = W
and T = N
then RAT WON
Question 61:
Complete the congruence statement:
Answer:
(i) Given that BT = BC
AT = AC
TBA = CBA
BCA BTA
(ii) Given that,
P = R
T = S
PT = QR
QRS TPQ
Question 62:
In a squared sheet, draw two triangles of equal areas such that
(i) the triangles are congruent.
(ii) the triangles are not congruent.
What can you say about their perimeters?
Answer:
In a square sheet, draw two triangles of equal
areas such that:
(i) the triangles are congruent, then their
perimeters are equal.
(ii) the triangles are not congruent, then their
perimeters are not equal.
Question 63:
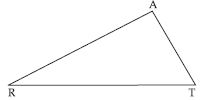
Draw a rough sketech of two triangles such that they have five pairs of congruent parts but still the triangles are not congruent.
Answer:
Here, P = A, Q = B, R = C
Also, PQ = AB, PR = BC
Question 64:
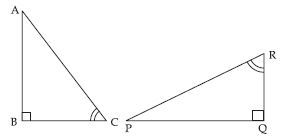
If ABC and PQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
Answer:
For ABC and PQR to be congruent we must need BC = QR
B = Q = 90
and C = R (Given)
By ASA congruence criterion,
ABC PQR
Question 65:
Explain, why ABC FED.
Answer:
Given that,
A = F
and B = E
Adding these, we get
A + B = F + E
or 180 – (A + B) = 180 – (F + E)
or C = D
Now, B = E = 90
BC = ED (Given)
and C = D (Proved)
By ASA congruence criterion,
ABC ≅ FED