NCERT Solutions for Class 7 Mathematics Chapter 10 - Perimeter and Area

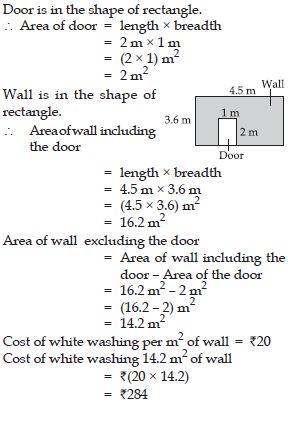
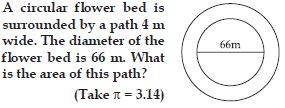
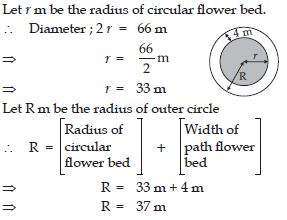
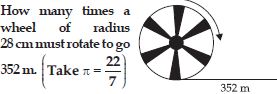
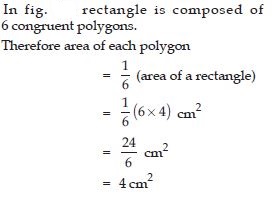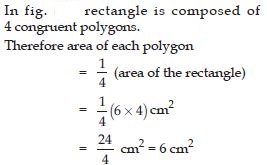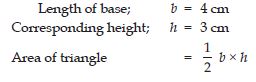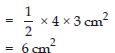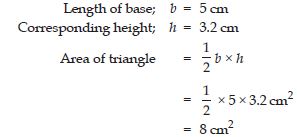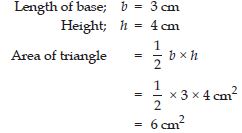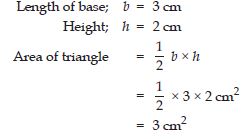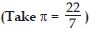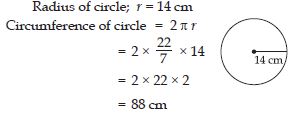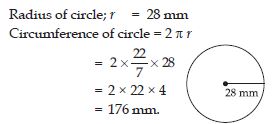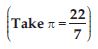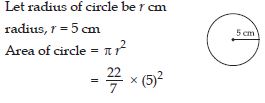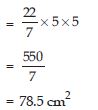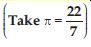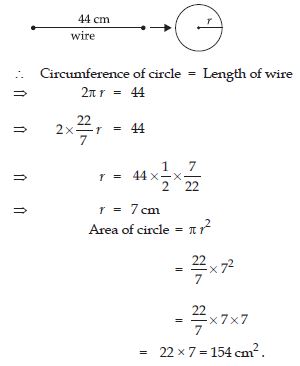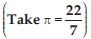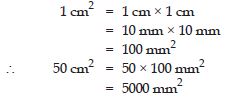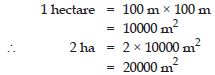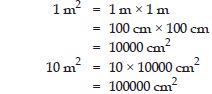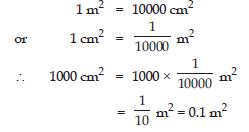Question 1:

Would you need to find, area or perimeter, to answer the following?
How much space does a blackboard occupy?

Question 2:

Would you need to find, area or perimeter, to answer the following?
What is the length of wire required to fence a rectangular flower bed?

Question 3:

What distance would you cover by taking two rounds of a triangular park?

Question 4:

How much plastic sheet do you need to cover a rectangular swimming pool?

Question 5:

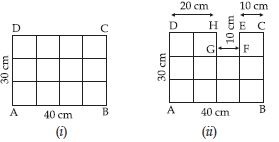
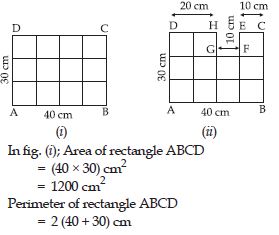
Compute their areas and perimeters.

Question 6:

The length and the breadth of a rectangular piece of land is 500 m by 300 m respectively. Find its area.

Question 7:

The length and the breadth of a rectangular piece of land is 500 m by 300 m respectively. Find the cost of the land, if 1 m² of the land costs ₹10,000.

Question 8:

Find the area of a square park whose perimeter is 320 m.

Question 9:

Find the breadth of a rectangular plot of land, if its area is 440 m² and the length is 22 m. Also find its perimeter.

Question 10:

The perimeter of a rectangular sheet is 100 cm. If the length is 35 cm, find its breadth. Also find the area.

Question 11:

The area of a square park is the same as of a rectangular park. If the side of the square park is 60 m and the length of the rectangular park is 90 m, find the breadth of the rectangular park.

Question 12:

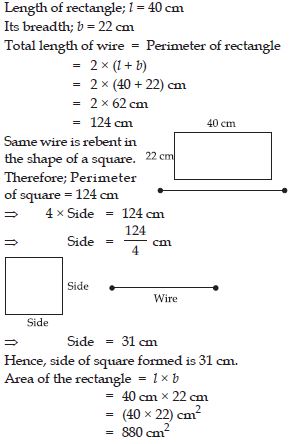
A wire is in the shape of a rectangle. Its length is 40 cm and breadth is 22 cm. If the same wire is rebent in the shape of a square, what will be the measure of each side? Also find which shape encloses more area?

Question 13:

The perimeter of a rectangle is 130 cm. If the breadth of the rectangle is 30 cm, find its length. Also find the area of the rectangle.

Question 14:

Question 15:

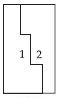
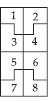
Each of the following rectangles of the length 6 cm and the breadth 4 cm is composed of congruent polygons. Find the area of each polygon.

Question 16:

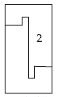
Each of the following rectangles of the length 6 cm and the breadth 4 cm is composed of congruent polygons. Find the area of each polygon.

Question 17:

Each of the following rectangles of the length 6 cm and the breadth 4 cm is composed of congruent polygons. Find the area of each polygon.

Question 18:

Each of the following rectangles of the length 6 cm and the breadth 4 cm is composed of congruent polygons. Find the area of each polygon.

Question 19:

Each of the following rectangles of the length 6 cm and the breadth 4 cm is composed of congruent polygons. Find the area of each polygon.

Question 20:

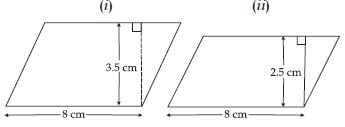
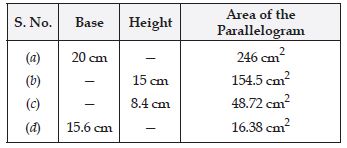
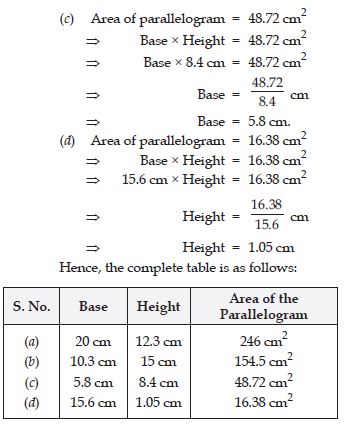
Find the area of following parallelograms:

(iii) In parallelogram ABCD, AB = 7.2 cm and the perpendicular from C on AB is 4.5 cm.

Question 21:

Find the area of each of the following parallelograms:

Question 22:

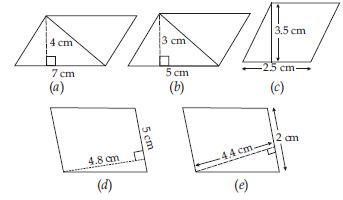
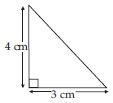
Find the area of the following triangles:

Question 23:

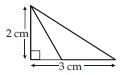
Find the area of the following triangles:

Question 24:

Find the area of the following triangles:

Question 25:

Find the area of the following triangles:

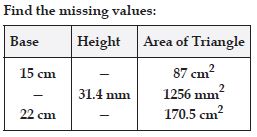
Question 26:

Find the missing values:

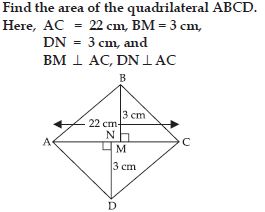
Question 27:

Question 28:

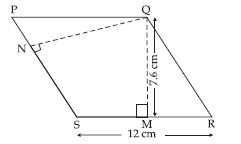
PQRS is a parallelogram. QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm, then find the area of the parallelogram PQRS

Question 29:

PQRS is a parallelogram. QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm, then find QN, if PS = 8 cm.

Question 30:

Question 31:

Question 32:

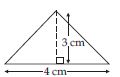
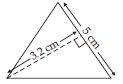
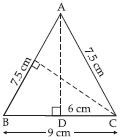
$∆$ABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm. The height AD from A to BC, is 6 cm. Find the area of $∆$ABC. What will be the height from C to AB i.e., CE?

Question 33:

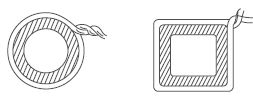
Which square has the larger perimeter?

Question 34:

Which is larger, perimeter of smaller square or circumference of the circle?

Question 35:

Find the circumference of the circles with the following radius:

Question 36:

Find the circumference of the circles with the following radius:

28 mm

Question 37:

Find the circumference of the circles with the following radius:

21 cm.

Question 38:

Find the area of the following circles, given that

radius = 14 mm

Question 39:

Find the area of the following circles, given that

Question 40:

Find the area of the following circles, given that

radius = 5 cm

Question 41:

Question 42:

Question 43:

From a circular of radius 4 cm, a circle of radius 3 cm is removed (fig). Find the area of the remaining sheet. (Take $\mathrm{\pi }$ = 3.14)

Question 44:

Saima wants to put a lace on the edge of a circular table cover of diameter 1.5 m. Find the length of the lace required and also find its cost if one metre of the lace costs ₹15. (Take $\mathrm{\pi }$ = 3.14)

Question 45:

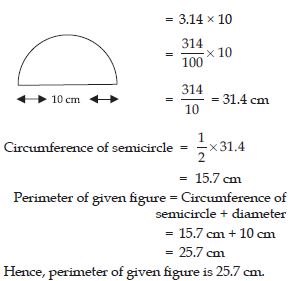
Find the perimeter of following figure, which is a semicircle including its diameter.

Question 46:

Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is ₹15 m². (Take $\mathrm{\pi }$ = 3.14)

Question 47:

Shazli took a wire of length 44 cm and bent it into the shape of a circle. Find the radius of that circle. Also find the area. If the same wire is bent into the shape of a square, what will be the length of each of its sides? Which figure encloses more area, the circle or square?

Question 48:

Question 49:

A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take $\mathrm{\pi }$ = 3.14)

Question 50:

The circumference of a circle is 31.4 cm. Find the radius and the area of the circle? (Take $\mathrm{\pi }$ = 3.14)

Question 51:

Question 52:

A circular flower garden has an area of 314 m². A sprinkler at the center of the garden can cover an area that has a radius of 12 m. Will the sprinkler water the entire garden? (Take $\mathrm{\pi }$ = 3.14)

Question 53:

Question 54:

Question 55:

The minute hand of a circular clock is 15 cm long. How far does the tip of the minute hand move in 1 hour? (Take $\mathrm{\pi }$ = 3.14)

Question 56:

50 cm² in mm²

Question 57:

2 ha in m²

Question 58:

10 m² in cm²

Question 59:

1000 cm² in m²

Question 60:

A garden is 90 m long and 75 m broad. A path 5 m wide is to be built outside around it. Find the area of the path. Also find the area of the garden in hectare.

Question 61:

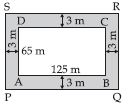
A 3 m wide path runs outside around a rectangular park of the length 125 m and the breadth 65 m. Find the area of the path.

Question 62:

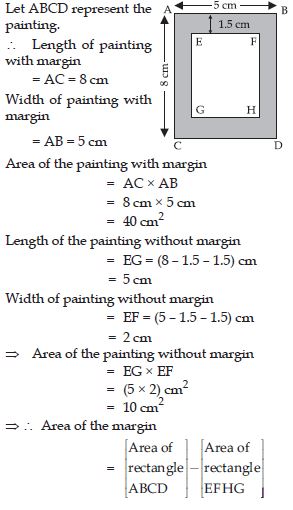
A picture is painted on a cardboard 8 cm long and 5 cm wide such that there is a margin of 1.5 cm along each of its sides. Find the total area of the margin.

Question 63:

A verandah of width 2.25 m wide is constructed all along outside of a room which is 5.5 m long and 4 m wide. Find:
(i) the area of the verandah.
(ii) the cost of cementing the floor of the verandah at the rate of ₹200 per m².

Question 64:

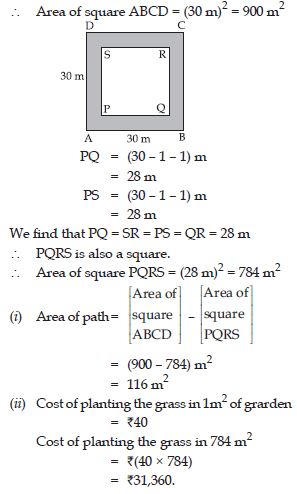
A path 1 m wide is built along the border inside a square garden of side 30 m. Find:
(i) the area of the path
(ii) the cost of planting the grass in the remaining portion of the garden at the rate of ₹40 per m².

Question 65:

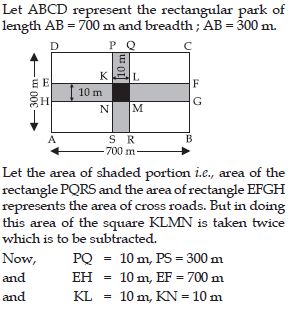
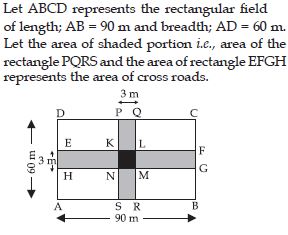
Two cross roads, each of width 10 m, cut at right angles through the centre of a rectangular park of the length 700 m and the breadth 300 m parallel to its sides. Find the area of the roads. Also find the area of park excluding cross roads give the answer in hectarees.

Question 66:

Through a rectangular field of the length 90 m and the breadth 60 m, two roads are constructed which are parallel to the sides and cut each other at right angles through the centre of the fields. If the width of each road is 3 m, find
(i) the area covered by the roads.
(ii) the cost of constructing the roads at the rate of ₹110 per m².

Question 67:

Pragya wrapped a cord around a circular pipe of radius 4 cm (shown below) and cut off the length required of the cord. Then she wrapped it around the square box of the side 4 cm (also shown). Did she have any cord left? ($\mathrm{\pi }$ = 3.14)

Question 68:

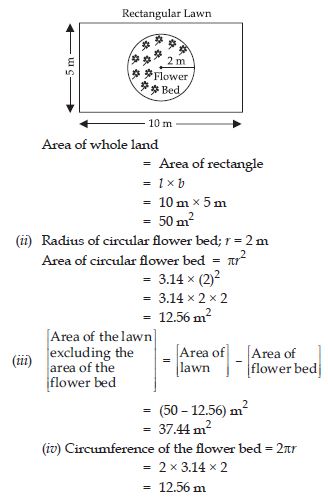
The figure represents a rectangular lawn with a circular flower bed in the middle. Find:
(i) the area of whole land
(ii) the area of flower bed
(iii) the area of the lawn excluding the area of the flower bed.
(iv) the circumference of the flower bed.

Question 69:

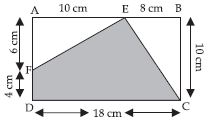
In the following figures, find the area of shaded portion.

Question 70:

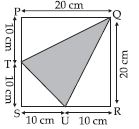
Find the area of shaded portion.

Question 71: