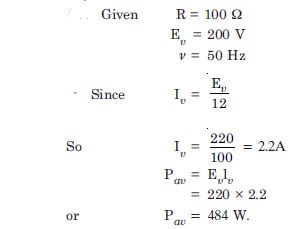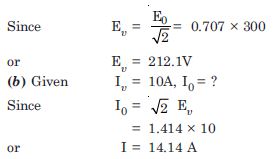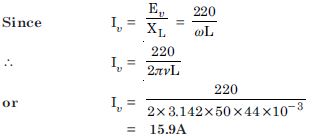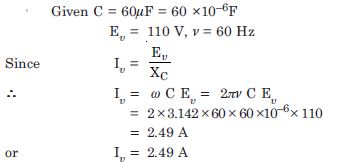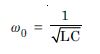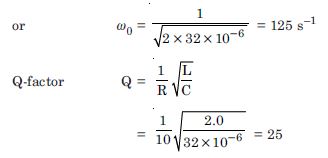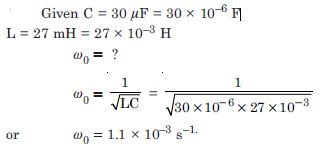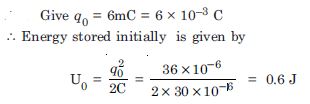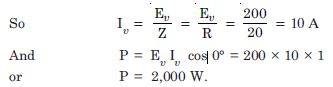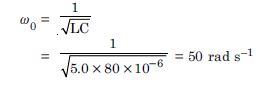Take the help of top NCERT Solutions for Class 12th at Aasoka. The platform provides free solutions to help students understand the concepts better and score good scores in their board exams as well as competitive exams. Students can boost their overall performance for exams with NCERT Solutions. These solutions are designed by subject matter experts as per the latest syllabus and exam pattern.
“Alternating Current” chapter of Physics Class 12 teach about series LCR circuit, capacitor, resistor, properties and powers of AC circuit, AC voltage, inductors, LC oscillations, transformers, and so much more. With the help of various diagrams and graphs, students will be able to easily understand the concept of the chapter. Studying, learning, and understanding this chapter will be beneficial for Class 12th board exams along with competitive exams.
Question 1:
A 100 resistor is connected to a 200 V, 50 Hz a.c. supply.
What is the rms value of current in the circuit ?
What is the net power consumed over a full cycle ?
Answer:
Question 2:
(a) The peak voltage of an ac supply is 300 V. What is the rms voltage ?
(b) The rms value of current in an a.c. circuit is 10 A. What is the peak current ?
Answer:
(a) Given E0 = 300 V, E = ?
Question 3:
A 44 mH inductor is connected to 220V, 50Hz a.c. supply. Determine the rms value of the current in the circuit.
Answer:
Given L = 44 mH = 44 ×10–3 H
E = 220 V, = 50 Hz
I = ?
Question 4:
A 60 F capacitor is connected to a 110V, 60 Hz a.c. supply. Determine the rms value of the current in the circuit.
Answer:
Question 5:
In Exercises 7.3 and 7.4, what is the net power absorbed by each circuit over a complete cycle. Explain your answer.
Answer:
In both the cases the net power consumed is
zero because in both the cases
Net power consumed
P = E I cos
and = 90
P = 0 (in each case)
Question 6:
Obtain the resonant frequency r of a series LCR circuit with L = 2.0 H, C = 32 F and R = 10 . What is the Q-value of this circuit ?
Answer:
Given L = 2.0 H,
C = 32 F = 32 × 10–6 F
R = 10 , Q = ?, 0. = ?
Resonant frequency
Question 7:
A charged 30 F, capacitor is connected to a 27 mH inductor. What is the angular frequency of free oscillations of the circuit ?
Answer:
Question 8:
Suppose the initial charge on the capacitor in Exercise 7.7 is 6 mC. What is the total energy stored in the circuit initially ? What is the total energy at later time ?
Answer:
Question 9:
A series LCR circuit with R = 20 ,
L = 1.5 H and C = 35 F is connected to a variable
frequency 200 V a.c. supply. When the frequency
of the supply equals the natural frequency
of the circuit, what is the average power transferred
to the circuit in one complete cycle ?
Answer:
Given R = 20 , L = 1.5 H,
C = 35 F = 35 ×10 –6 F
E = 200
When frequency of supply equals the natural frequency
of the circuit, we get resonance condition.
Z = R = 20
Question 10:
A radio can tune over the frequency range of a portion of MW broadcast band : (800 kHz to 1200 kHz). If its circuit has an effective inductance of 200 μH, what must be the range of its variable capacitor ? [Hint. For tuning, the natural frequency i.e., the frequency of free oscillations of the LC circuit should be equal to the frequency of the radio wave.]
Answer:
Since
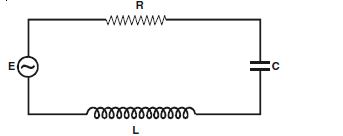
Question 11:
Figure TBQ 7.11 shows a series LCR
circuit connected to a variable frequency 230 V source.
L = 5.0 H, C = 80 μF, R = 40
Determine the source frequency which drives the circuit in resonance.
Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
Determine the rms potential drop across the three elements of the circuit. Show that the potential drop across the LC combination is zero at the resonating frequency.
Answer:
Resonant frequency