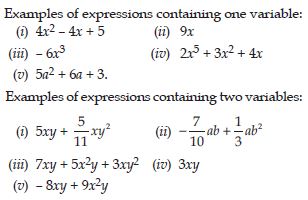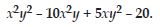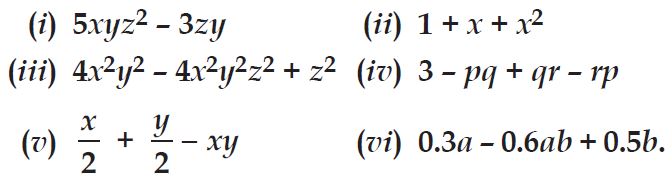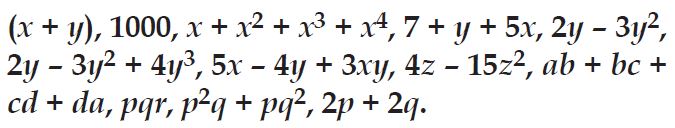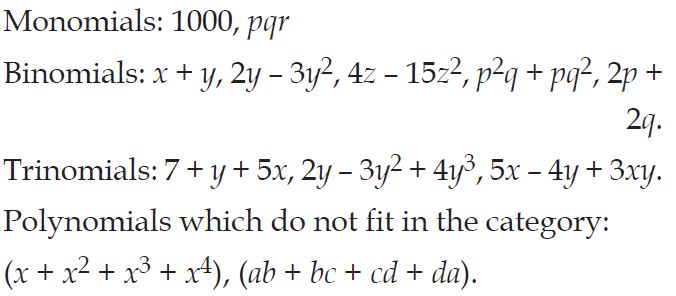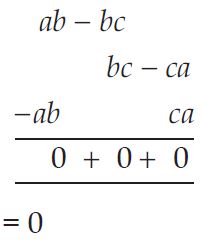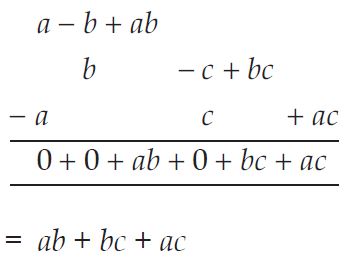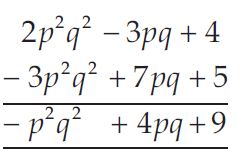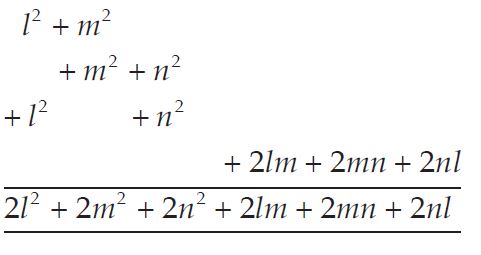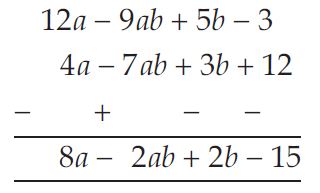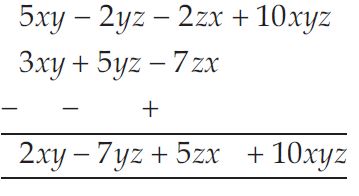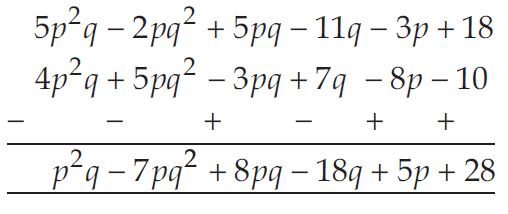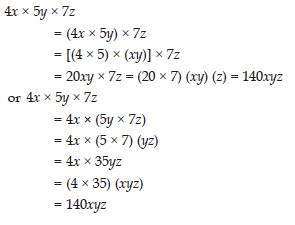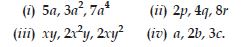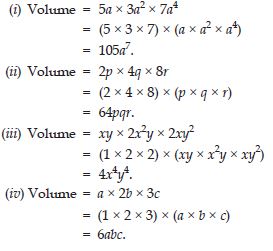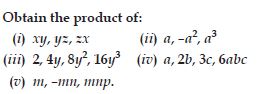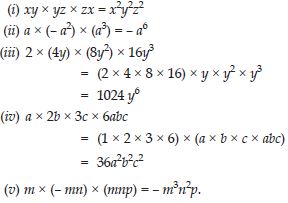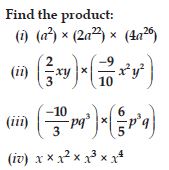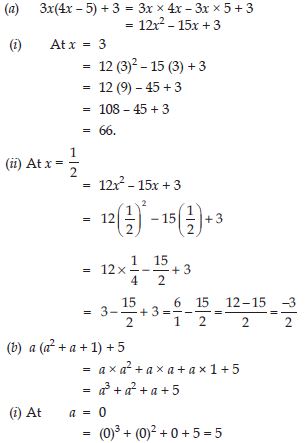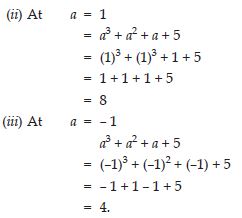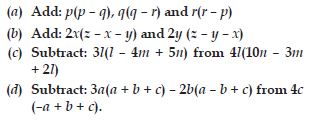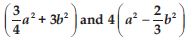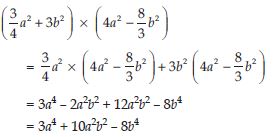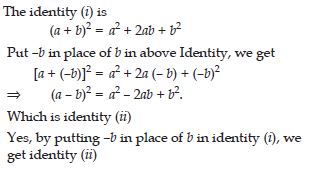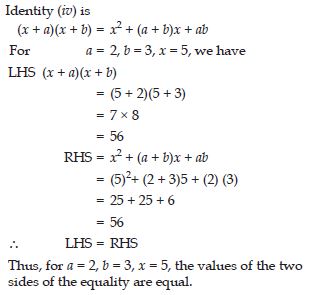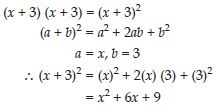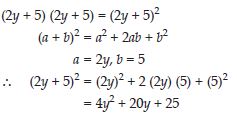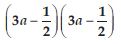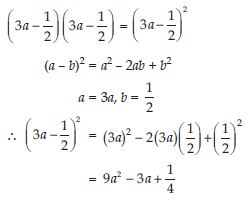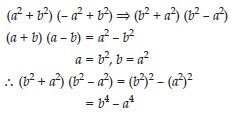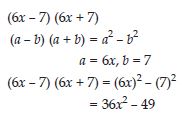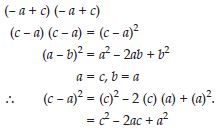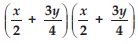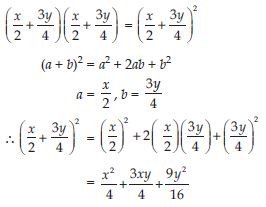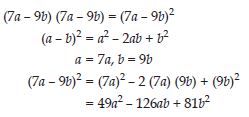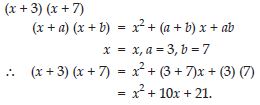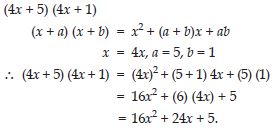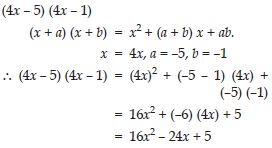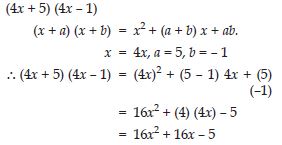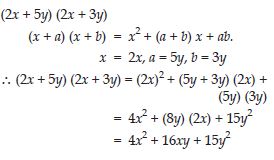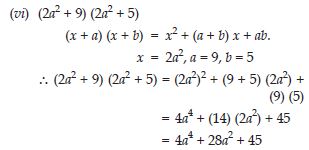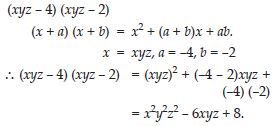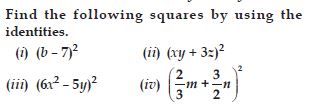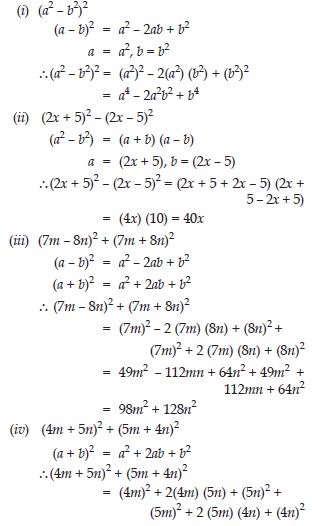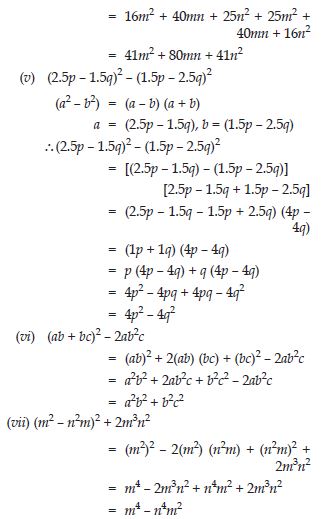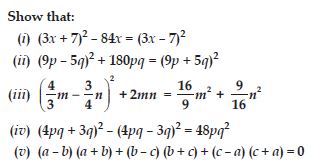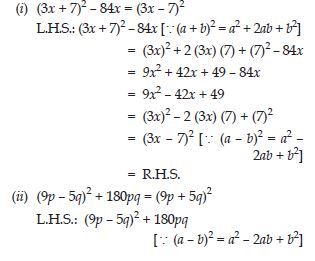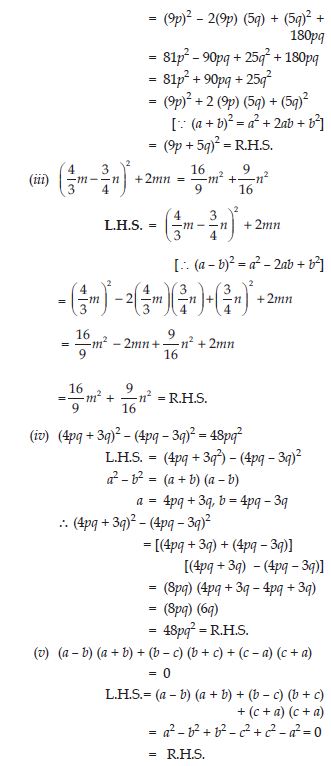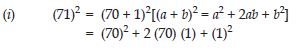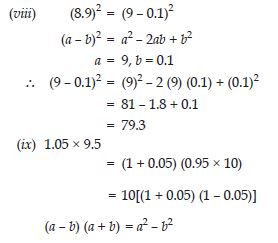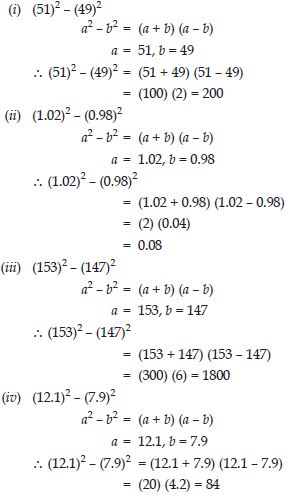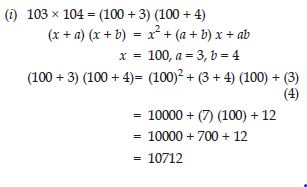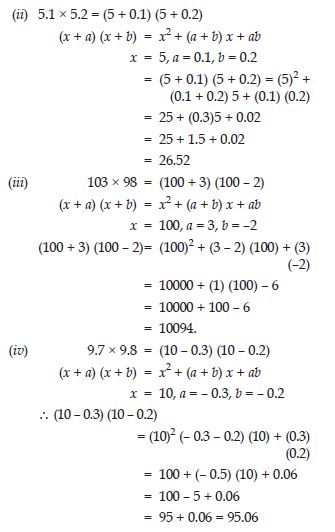NCERT Solutions for Class 8 Algebraic Expressions and Identities

Question 1:

Give five examples of expressions containing one variable and five examples of expressions containing two variables.

Answer:

Show Answer

Question 2:

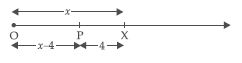
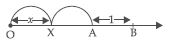
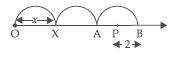
Show on the number line x, x - 4, 2x + 1, 3x - 2.

Answer:

Let us say the variable x has a position X on the number line

The value of x - 4 will be 4 units to the left of X

The position of 2x will be point A, the distance of A from the origin will be twice the distance of X from the origin. The position B of 2x + 1 will be 1 unit to the right of A.

The position of 3x will be point B; the distance of B from origin will be three times the distance of X from the origin. The position P of 3x - 2 will be 2 units to the left of B.

Show Answer

Question 3:

Identify the coefficients of each term in the expression:

Answer:

Coefficient of x²y² is 1
Coefficient of x²y is -10
Coefficient of xy² is 5
Constant term is -20.

Show Answer

Question 4:

Classify the following polynomials as monomials, binomials, trinomials:
-z + 5, x + y + z, y + z + 100, ab - ac, 17.

Answer:

Monomials: 17
Binomials: -z + 5, ab - ac
Trinomials: x + y + z, y + z + 100.

Show Answer

Question 5:

Construct 3 binomials with only x as a variable.

Answer:

Binomials having x as a variable:
(i) 3x² + 5x (ii) 6x³ + 2x (iii) 9x + 4x³

Show Answer

Question 6:

Construct 3 binomials with x and y as variable.

Answer:

Binomials having x and y as variables:
(i) 3x² y + 4xy (ii) 9xy + 6xy² (iii) 5xy + 8x² y

Show Answer

Question 7:

Construct 3 monomials with x and y as variables.

Answer:

Monomials with x and y as variables:
(i) 4x²y (ii) 5xy² (iii) 3xy

Show Answer

Question 8:

Construct 2 polynomials with 4 or more terms.

Answer:

Polynomials having 4 or more terms:
(i) a + b + c + d
(ii) 2x³+ 5x² + 3x + 18
(iii) 3x² + 4xy + y² + y + x + 9.

Show Answer

Question 9:

Write two terms which are like:
(i) 7xy (ii) 4 mn² (iii) 2l.

Answer:

(i) Terms which are like 7xy:
3xy, 9xy etc.
(ii) Terms which are like 4 mn²:
9mn², mn² etc.
(iii) Terms which are like 2l:
6l, 9l, 5l etc.

Show Answer

Question 10:

Identify the terms, their coefficients for each of the following expressions:

Answer:

Show Answer

Question 11:

Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any of these three categories?

Answer:

Show Answer

Question 12:

Add the following:
ab - bc, bc - ca, ca - ab

Answer:

Show Answer

Question 13:

Add the following:
a - b + ab, b - c + bc, c - a + ac.

Answer:

Show Answer

Question 14:

Add the following:
2p²q² - 3pq + 4, 5 + 7pq - 3p²q²

Answer:

Show Answer

Question 15:

Add the following:
l² + m², m² + n², n² + l², 2lm + 2mn + 2nl

Answer:

Show Answer

Question 16:

Subtract 4a - 7ab + 3b +12 from 12a - 9ab + 5b - 3

Answer:

Show Answer

Question 17:

Subtract 3xy + 5yz - 7zx from 5xy - 2yz - 2zx + 10xyz

Answer:

Show Answer

Question 18:

Subtract 4p²q - 3pq + 5pq² - 8p + 7q - 10 from
18 - 3p - 11q + 5pq - 2pq² + 5p²q.

Answer:

Show Answer

Question 19:

Find 4x x 5y x 7z.
Does the order in which you carry out the multiplication matter?

Answer:

The result is same in both the cases.
No, the order of multiplication does not alter the result.

Show Answer

Question 20:

Find the product of the following pairs of monomials:
(i) 4, 7p
(ii) -4p, 7p
(iii) -4p, 7pq
(iv) 4p3, -3p
(v) 4p, 0

Answer:

(i) 4 x 7p = 28p
(ii) -4p x 7p = (-4 x 7) x (p x p) = -28p²
(iii) -4p x 7pq = (-4 x 7) x (p x pq) = -28p²q
(iv) 4p3 x -3p = [4 x (-3)] x (p³ x p) = -12p⁴
(v) 4p x 0 = 0.

Show Answer

Question 21:

Find the areas of rectangles with the following pairs of monomials as their lengths and breadths respectively:
(p, q); (10 m, 5n); (20x², 5y²); (4x, 3x²); (3mn, 4np).

Answer:

(i) Length of rectangle = p
Breadth of rectangle = q
Area of rectangle = length x breadth = p x q = pq.
(ii) Length of rectangle = 10 m
Breadth of rectangle = 5n
Area of rectangle = length x breadth = 10m x 5n
= 50mn.
(iii) Length of rectangle = 20x²
Breadth of rectangle = 5y²
Area of rectangle = length x breadth
= 20x² x 5y²
= 100x²y².
(iv) Length of rectangle = 4x
Breadth of rectangle = 3x²
Area of rectangle = length x breadth
= 4x x 3x²
= 12x³.
(v) Length of rectangle = 3mn
Breadth of rectangle = 4np
Area of rectangle = length x breadth = 3mn x 4np
= 12mn²p.

Show Answer

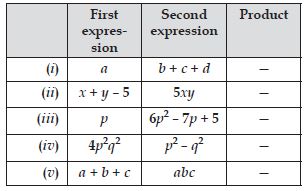
Question 22:

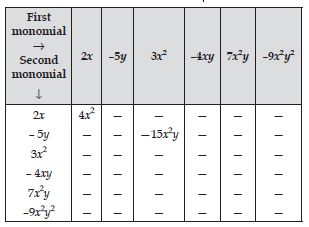
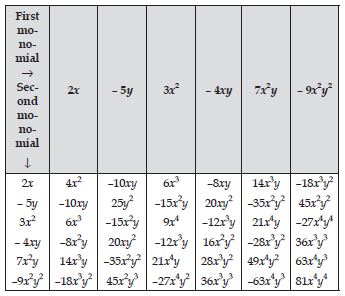
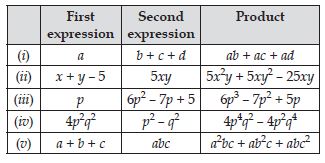
Complete the table of products:

Answer:

Complete table of products is as under:

Show Answer

Question 23:

Obtain the volume of rectangular boxes with the following length, breadth and height respectively.

Answer:

Show Answer

Question 24:

Answer:

Show Answer

Question 25:

Find the product:
(i) 2x(3x + 5xy) (ii) a²(2ab – 5c)

Answer:

(i) (2x) x (3x + 5xy)
= (2x) x (3x) + (2x) x (5xy)
= 6x² + 10x²y.
(ii) a² (2ab – 5c)
= a² x 2ab – a² x 5c
= 2a³b – 5a²c.

Show Answer

Question 26:

Find the product: (4p² + 5p + 7) x 3p.

Answer:

4p² x 3p + 5p x 3p + 7 x 3p
= 12p³ + 15p² + 21p.

Show Answer

Question 27:

Carry out the multiplication of the expressions in each of the following pairs:
(i) 4p, q + r (ii) ab, a – b
(iii) a + b, 7a²b² (iv) a² – 9, 4a
(v) pq + qr + rp, 0

Answer:

Show Answer

Question 28:

Complete the table:

Answer:

Show Answer

Question 29:

Answer:

Show Answer

Question 30:

Answer:

Show Answer

Question 31:

Answer:

Show Answer

Question 32:

Multiply the binomials: (2x + 5) and (4x – 3)

Answer:

(2x + 5) x (4x – 3)
= 2x x (4x – 3) + 5 (4x – 3)
= 2x x 4x – 2x x 3 + 5 x 4x – 5 x 3
= 8x² – 6x + 20x – 15
= 8x² + 14x – 15

Show Answer

Question 33:

Multiply the binomials: (y – 8) and (3y – 4)

Answer:

(y – 8) x (3y – 4)
= y (3y – 4) – 8 x (3y – 4)
= 3y² – 4y – 24y + 32
= 3y² – 28y + 32

Show Answer

Question 34:

Multiply the binomials: (2.5l – 0.5m) and (2.5l + 0.5m)

Answer:

(2.5l – 0.5m) x (2.5l + 0.5m)
= 2.5l x (2.5l + 0.5m) – 0.5m (2.5l + 0.5m)
= 6.25l² + 1.25lm – 1.25lm – 0.25m²
= 6.25l² – 0.25m²

Show Answer

Question 35:

Multiply the binomials: (a + 3b) and (x + 5)

Answer:

(a + 3b) x (x + 5)
= a x (x + 5) + 3b x (x + 5)
= ax + 5a + 3bx + 15b
= 5a + (a + 3b) x + 15b

Show Answer

Question 36:

Multiply the binomials: (2pq + 3q²) and (3pq – 2q²)

Answer:

(2pq + 3q²) x (3pq – 2q²)
= 2pq x (3pq – 2q²) + 3q² x (3pq – 2q²)
= 6p²q² – 4pq³ + 9pq³ – 6q⁴
= 6p²q² + 5pq³ – 6q⁴.

Show Answer

Question 37:

Multiply the binomials:

Answer:

Show Answer

Question 38:

Find the product: (5 – 2x) (3 + x)

Answer:

(5 – 2x) (3 + x)
= 5 x (3 + x) – 2x x (3 + x)
= 15 + 5x – 6x – 2x²
= 15 – x – 2x²

Show Answer

Question 39:

Find the product: (x + 7y) (7x – y)

Answer:

(x + 7y) (7x – y)
= x x (7x – y) + 7y x (7x – y)
= 7x² – xy + 49xy – 7y²
= 7x² + 48xy – 7y²

Show Answer

Question 40:

Find the product: (a² + b) (a + b²)

Answer:

(a² + b) (a + b²)
= a² (a + b²) + b (a + b²)
= a³ + a²b² + ab + b³

Show Answer

Question 41:

Find the product: (p² – q²) (2p + q)

Answer:

(p² – q²) (2p + q) = p² (2p + q) – q² (2p + q)
= 2p³ + p²q – 2pq² – q³

Show Answer

Question 42:

Simplify:
(x² – 5) (x + 5) + 25

Answer:

(x² – 5) (x + 5) + 25
= x² (x + 5) – 5 (x + 5) + 25
= x³ + 5x² – 5x – 25 + 25
= x³ + 5x² – 5x

Show Answer

Question 43:

Simplify:
(a² + 5) (b³ + 3) + 5

Answer:

(a² + 5) (b³ + 3) + 5
= a² (b³ + 3) + 5 (b³ + 3) + 5
= a²b³ + 3a² + 5b³ + 15 + 5
= a²b³ + 3a² + 5b³ + 20

Show Answer

Question 44:

Simplify:
(t + s²) (t² – s)

Answer:

(t + s²) (t² – s)
= t (t² – s) + s² (t² – s)
= t³ – ts + s²t² – s³

Show Answer

Question 45:

Simplify:
(a + b) (c – d) + (a – b) (c + d) + 2 (ac + bd)

Answer:

(a + b) (c – d) + (a – b) (c + d) + 2 (ac + bd)
= a(c – d) + b(c – d) + a(c + d) – b(c + d) + 2ac + 2bd
= ac – ad + bc – bd + ac + ad – bc – bd + 2ac + 2bd
= 4ac

Show Answer

Question 46:

Simplify:
(x + y) (2x + y) + (x + 2y) (x – y)

Answer:

(x + y) (2x + y) + (x + 2y) (x – y)
= x(2x + y) + y(2x + y) + x(x – y) + 2y(x – y)
= 2x² + xy + 2xy + y² + x² – xy + 2xy – 2y²
= 3x² + 4xy – y²

Show Answer

Question 47:

Simplify:
(x + y) (x² – xy + y²)

Answer:

(x + y) (x² – xy + y²)
= x (x² – xy + y²) + y (x² – xy + y²)
= x³ – x²y + xy² + yx² – xy² + y³
= x³ + y³

Show Answer

Question 48:

Simplify:
(1.5x – 4y) (1.5x + 4y + 3) – 4.5x + 12y

Answer:

(1.5x – 4y) (1.5x + 4y + 3) – 4.5x + 12y
= 1.5x(1.5x + 4y + 3) – 4y (1.5x + 4y + 3) – 4.5x + 12y
= 2.25x² + 6xy + 4.5x – 6xy – 16y² – 12y – 4.5x + 12y
= 2.25x² – 16y²

Show Answer

Question 49:

Simplify:
(a + b + c) (a + b – c)

Answer:

(a + b + c) (a + b – c)
= a (a + b – c) + b (a + b – c) + c (a + b – c)
= a² + ab – ac + ab + b² – bc + ac + bc – c²
= a² + b² – c² + 2ab

Show Answer

Question 50:

Put –b in place of b in Identity (i): (a + b)² = a² + 2ab + b². Do you get Identity (ii): (a – b)² = a² – 2ab + b²?

Answer:

Show Answer

Question 51:

Verify identity (iv): (x + a)(x + b) = x² + x(a + b) + ab for a = 2, b = 3, x = 5.

Answer:

Show Answer

Question 52:

Consider, the special case of identity (iv): (x + a)(x + b)= x² + x(a + b) + ab with a = b, what do you get? Is it related to Identity (i): (x + a)² = x² + 2ax + a²?

Answer:

The Identity (iv) is
(x + a) (x + b) = x² + (a + b)x + ab
For a = b the above identity becomes
(x + a)(x + a) = x² + (a + a) x + a.a
$\Rightarrow$ (x + a)² = x² + 2ax + a²
Yes, it is related to identity (x + a)² = x² + 2ax + a².

Show Answer

Question 53:

Consider, the special case of identity (iv): (x + a)(x + b)= x² + x(a + b) + ab with a = –c and b = –c. What do you get? Is it related to Identity (ii): (x – c)² = x² – 2cx + c²?

Answer:

The Identity (iv) is
(x + a) (x + b) = x² + (a + b) x + ab
For a = – c and b = – c the identity (iv) becomes
[x + (–c)][x + (– c)] = x² + [( – c) + (–c)]x + (– c)(– c)
$\Rightarrow$ (x – c) (x – c) = x² + ( –2c) x + c²
$\Rightarrow$ (x – c) (x – c) = x² – 2 cx + c²
$\Rightarrow$ (x – c)² = x² – 2cx + c²
Yes, it is related to identity (ii).

Show Answer

Question 54:

Consider the special case of identity (iv): (x + a)(x + b)= x² + x(a + b) + ab with b = –a. What do you get? Is it related to identity (iii): (x – c)² = x² – 2cx + c².

Answer:

The identity (iv) is
(x + a) (x + b) = x² + (a + b) x + ab
For b = – a, identity (iv) becomes
(x + a) [x + (– a)] = x² + [(a) + (–b)]x + (a)(– a)
$\Rightarrow$ (x + a) (x – a) = x² + (a – a)x – a²
$\Rightarrow$ (x + a) (x – a) = x² + (0)x – a²
$\Rightarrow$ (x + a) (x – a) = x² – a².
Yes, it is related to identity (iii): (x – c)² = x² – 2cx + c².