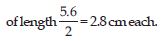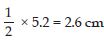Question 1:
Arshad has five measurements of a quadrilateral ABCD. These are AB = 5 cm, A = 50°, AC = 4 cm, BD = 5 cm and AD = 6 cm. Can he construct a unique quadrilateral? Give reasons for your answer.
Answer:
We cannot construct a unique quadrilateral because we can construct ABD but not BCD.
Similarly, neither we can construct ACD nor ABC.
Question 2:
We saw that 5 measurement of a quadrilateral can determine a quadrilateral uniquely. Do you think any five measurement of the quadrilateral can do this?
Answer:
No, any five measurements cannot determine a quadrilateral uniquely.
Question 3:
Can you draw a parallelogram. BATS where BA = 5 cm, AT = 6 cm and AS = 6.5 cm? Why?
Answer:
Yes, we can draw a parallelogram BATS because the opposite sides of a parallelogram are equal in length.
Question 4:
Can you draw a rhombus ZEAL where ZE = 3.5 cm, diagonal EL = 5 cm? Why?
Answer:
Yes, we can draw a rhombus ZEAL because all the four sides of a rhombus are equal in length.
Question 5:
A student attempted to draw a quadrilateral PLAY where PL = 3 cm, LA = 4 cm,
AY = 4.5 cm, PY = 2 cm and LY = 6 cm, but could not draw it. What is the reason?
[Hint: Discuss it using a rough sketch].
Answer:
The student could not draw it because PL + PY < LY.
Question 6:
Construct the following quadrilaterals:
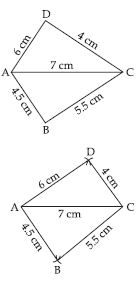
Quadrilateral ABCD
AB = 4.5 cm, BC = 5.5 cm, CD = 4 cm,
AD = 6 cm, AC = 7 cm
Answer:
Given: Four sides of a quadrilateral and one
diagonal, as given below:
AB = 4.5 cm, BC = 5.5 cm, CD = 4 cm,
AD = 6 cm, AC = 7 cm.
First, we draw a rough sketch to represent the given data.
Steps of Construction:
(i) Take a line segment AC = 7 cm.
(ii) With A as centre and radius AD = 6 cm draw an arc.
(iii) With C as centre and radius CD = 4 cm draw another arc cutting first arc at D.
(iv) Join AD and CD.
(v) With A as centre and radius AB = 4.5 cm, draw an arc.
(vi) With C as centre and radius BC = 5.5 cm, draw another arc intersecting the first arc at B.
(vii) Join AB and BC.
Then, ABCD is the required quadrilateral.
Question 7:
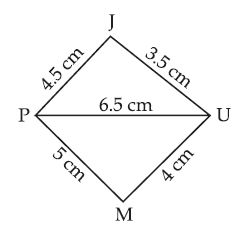
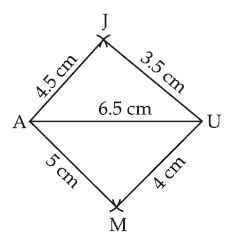
Construct the following quadrilaterals:
Quadrilateral JUMP
JU = 3.5 cm, UM = 4 cm, MP = 5 cm,
PJ = 4.5 cm, PU = 6.5 cm
Answer:
Given: Four sides of a quadrilateral and one
diagonal as:
JU = 3.5 cm, UM = 4 cm, MP = 5 cm,
PJ = 4.5 cm, PU = 6.5 cm.
Steps of Construction:
First, draw a rough sketch to
represent the above data.
(i) Take a line segment
PU = 6.5 cm.
(ii) With P as centre and radius PJ = 4.5 cm, draw an arc.
(iii) With U as centre and radius UJ = 3.5 cm, draw another arc intersecting the first arc at J.
(iv) Join PJ and JU.
(v) With P as centre and radius PM = 5 cm, draw an arc.
(vi) With U as centre and radius UM = 4 cm, drawn another arc intersecting the first arc at M.
(vii) Join PM and UM.
Then, JUMP is the required quadrilateral.
Question 8:
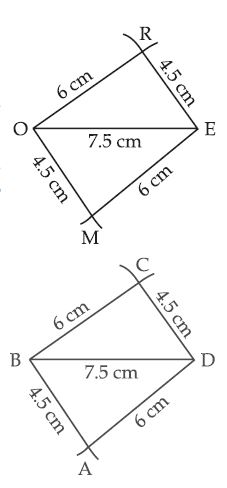
Construct the following quadrilaterals:
Parallelogram MORE
OR = 6 cm, RE = 4.5 cm, EO = 7.5 cm
Answer:
Given: Adjacent sides of a parallelogram and one
diagonal as:
OR = 6 cm, RE = 4.5 cm and EO = 7.5 cm.
Steps of Construction:
(i) Take a line segment OE = 7.5 cm
(ii) With O as centre and radius OR = 6 cm draw an arc.
(iii) With E as centre and radius ER = 4.5 cm draw another arc cutting first arc at R.
(iv) Join OR and ER.
(v) With O as centre and radius OM = 4.5 cm, draw an arc.
(vi) With E as centre and radius EM = 6 cm draw another arc cutting first arc at M.
(vii) Join OM and EM.
Then, MORE is the required parallelogram.
Question 9:
Construct the following quadrilaterals:
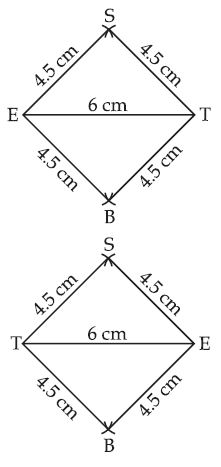
Rhombus BEST
BE = 4.5 cm, ET = 6 cm
Answer:
Let the Rhombus to be constructed is BEST,
BE = ES = ST = TB = 4.5 cm and diagonal ET = 6 cm.
First we draw a rough sketch of the given data.
Steps of Construction:
(i) Take a line segment ET = 6 cm.
(ii) With E as centre and radius ES = EB = 4.5 cm, draw two arcs on the either sides of ET.
(iii) With T as centre and
radius TS = TB = 4.5 cm,
draw arcs intersecting the
arcs in step (ii) at S and B
respectively.
(iv) Join ES, ST, BE and BT.
Then, BEST is the required
rhombus.
Question 10:
Can you construct a quadrilateral PQRS with
PQ = 3 cm, RS = 3 cm, PS = 7.5 cm, PR = 8 cm and
SQ = 4 cm? Justify your answer.
Answer:
No, we cannot construct a quadrilateral PQRS.
Because in PQS, PQ + SQ < OS (the sum of the
length of any two sides of a triangle must always
be greater than the third side).
Question 11:
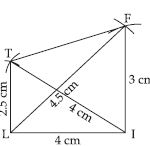
Construct the following quadrilaterals:
Quadrilateral LIFT
LI = 4 cm, IF = 3 cm, TL = 2.5 cm, LF = 4.5 cm, IT = 4 cm.
Answer:
Given: Three sides and two diagonals of the
quadrilateral LIFT.
i.e., LI = 4 cm, IF = 3 cm, TL = 2.5 cm
LF = 4.5 cm, IT = 4 cm.
Steps of Construction:
(i) Take a line segment
LI = 4 cm.
(ii) With I as centre and radius 3 cm. draw an arc.
(iii) With L as centre and radius 4.5 cm draw an arc, which intersects the previous arc at F.
(iv) Join LF and IF.
(v) With L as centre and radius 2.5 cm, draw an arc.
(vi) With I as centre and radius 4 cm, draw an arc, which cuts the previous arc at T.
(vii) Join LI, IT and FT.
∴ LIFT is the required quadrilateral.
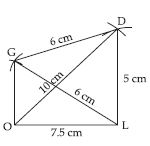
Question 12:
Construct the following quadrilaterals:
Quadrilateral GOLD
OL = 7.5 cm, GL = 6 cm, GD = 6 cm, LD
= 5 cm, OD = 10 cm
Answer:
Given: Three sides
and two diagonals
of the quadrilateral
GOLD.
i.e., OL = 7.5 cm,
GL = 6 cm, GD =
6 cm, LD = 5 cm,
OD = 10 cm.
Steps of Construction:
(i) Take a line segment OL = 7.5 cm.
(ii) With O as centre and radius 10 cm, draw an arc.
(iii) With L as centre and radius 5 cm, draw an arc, which intersects the previous arc at D.
(iv) Join OD and LD.
(v) With D as centre, and radius 6 cm, draw an arc.
(vi) With L as centre, and radius 6 cm, draw an
arc, which intersects the previous arc at G.
(vii) Join GL, GD and OG.
∴ GOLD is the required quadrilateral.
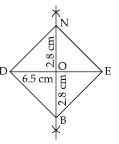
Question 13:
Construct the following quadrilaterals:
Rhombus BEND
BN = 5.6 cm, DE = 6.5 cm.
Answer:
Given: Two diagonals of the rhombus BEND.
i.e., BN = 5.6 cm, DE = 6.5 cm.
Steps of Construction:
(i) Take a line segment DE = 6.5 cm.
(ii) Bisect the line segment DE.
(iii) With O as centre, draw arcs
Above and below the line DE, which intersect the bisector at point N and D respectively.
(iv) Join BE, EN, ND and BD.
∴ BEND is the required Rhombus.
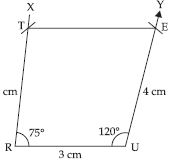
Question 14:
Can you construct a quadrilateral MIST where MI = 3.5 cm, IS = 6.5 cm, M = 75°, I = 105° and S = 120°.
Answer:
Yes, we can construct the quadrilateral MIST.
Because the sum of all the four angles is equal to 360°.
Question 15:
Can you construct the quadrilateral PLAN if PL = 6 cm, LA = 9.5 cm, P = 75°, L = 150° and A = 140°? (Hint: Recall angle-sum property).
Answer:
No, we cannot construct the quadrilateral PLAN.
Because the sum of all the four angles is greater than 360°.
Question 16:
In a parallelogram, the lengths of adjacent sides are known. Do we still need measures of the angles to construct as in the example above?
Answer:
Yes, we still need the measure of angles between adjacent sides to construct the parallelogram.
Question 17:
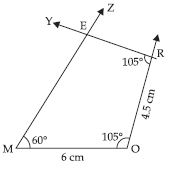
Construct the following quadrilaterals:
Quadrilateral MORE
MO = 6 cm, OR = 4.5 cm, M = 60°,
O = 105°, R = 105°
Answer:
Given: Two adjacent sides and three angles
of the quadrilateral MORE.
i.e., MO = 6 cm, OR = 4.5 cm,
M = 60°, O = 105°, R = 105°.
Steps of Construction:
(i) Draw MO = 6 cm.
(ii) At O; draw an angle XOM = 105°.
(iii) From ray OX, cut OR = 4.5 cm.
(iv) At R; draw an angle YRO = 105°.
(v) At M, draw an angle ZMO = 60° and let,
rays RY and MZ intersect each other at E.
∴ MORE is the required quadrilateral.
Question 18:
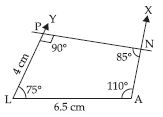
Construct the following quadrilaterals:
Quadrilateral PLAN
PL = 4 cm, LA = 6.5 cm, P = 90°,
A = 110°, N = 85°
Answer:
Given: Two adjacent sides and three angles of
the quadrilateral PLAN.
i.e., PL = 4 cm, LA = 6.5 cm, P = 90°,
A = 110°, N = 85°.
Steps of Construction:
(i) Draw LA = 6.5 cm.
(ii) At A, draw an
angle XAL =
110°.
(iii) At L, draw an
angle YLA = 75°.
∴ By angle sum property;
P + L + A + N = 360°
90° + L + 110° + 85° = 360°
L + 285° = 360°
⇒ L = 360° – 285° = 75°
(iv) From ray LY, cut LP = 4 cm.
(v) At P draw angle of 90°, which intersects the
ray AX at N.
∴ PLAN is the required quadrilateral.
Question 19:
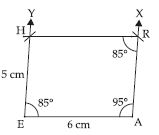
Construct the following quadrilaterals:
Parallelogram HEAR
HE = 5 cm, EA = 6 cm, R = 85°
Answer:
Given: Two adjacent sides and one angle of the
parallelogram.
i.e., HE = 5 cm, EA = 6 cm and R = 85°.
Steps of Construction:
(i) Draw EA = 6 cm.
(ii) At A draw an
angle XAE = 95°.
From ray AX cut
AR = 5 cm.
(iii) At E draw an angle
YEA = 85°. From
ray EY cut HE = 5
cm.
(iv) Join HR.
∴ HEAR is the required parallelogram.
Question 20:
Construct the following quadrilaterals:
Rectangle OKAY
OK = 7 cm, KA = 5 cm
Answer:
Given: Two adjacent sides of a rectangle OKAY.
i.e., OK = 7 cm and KA = 5 cm.
As each angle of a rectangle is of 90°.
Steps of Construction:
(i) Draw OK = 7 cm.
(ii) At points O and K
draw angles of
90° each i.e.,
XKO and
POK.
(iii) From XK cut, AK =5 cm.
(iv) From PO cut, OY = 5 cm.
(v) Join AY.
∴ OKAY is the required rectangle.
Question 21:
Consider to construct a quadrilateral ABCD, where AB = 4 cm, BC = 5 cm, CD = 6.5 cm and B = 105°, C = 80° using BC as base. Instead, what could have been be the other starting points?
Answer:
Yes, we could have first drawn AB or CD.
Question 22:
We used some five measurements to draw
quadrilaterals so far. Can there be different
sets of five measurements (other than seen so
far) to draw a quadrilateral? The following
problems may help you in answering the
questions.
(i) Quadrilateral ABCD with AB = 5 cm, BC = 5.5 cm, CD = 4 cm, AD = 6 cm and B =
80°
(ii) Quadrilateral PQRS with PQ = 4.5 cm, P
= 70°, Q = 100°, R = 80° and S= 110°.
Construct a few more examples of your
own of find sufficiency/insufficiency of the
data for construction of a quadrilateral.
Answer:
(i) We used five measurements to draw a
quadrilaterals.
(ii) We cannot draw a quadrilaterals using five
measurements.
Few more examples,
(a) Draw a quadrilateral ABCD in which AB =
6.5 cm, BC = 4 cm, CD = 4.5 cm, B = 60°
and AB|| CD.
(b) Draw another quadrilateral ABCD in which
AB = 7.5 cm, AD = 5 cm, BC = 5 cm, A =
90° and BC|| AD.
Question 23:
Construct the following quadrilaterals:
Quadrilateral DEAR
DE = 4 cm, EA = 5 cm, AR = 4.5 cm,
E = 60°, A = 90°
Answer:
Given: Three sides and two included
angles of the quadrilateral DEAR are given
i.e., DE = 4 cm, EA = 5 cm, AR = 4.5 cm,
E = 60°, A = 90°
Steps of Construction:
(i) Draw a line segment DE = 4 cm.
(ii) At point E, make an DEX = 60° and cut an arc of length 5 cm from E, which intersect EX at A.
(iv) Join DR.
∴ DEAR is the required quadrilateral.
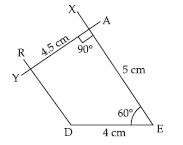
Question 24:
Construct the following quadrilaterals:
Quadrilateral TRUE
TR = 3.5 cm, RU = 3 cm, UE = 4 cm,
R = 75°, U = 120°
Answer:
Given: Three sides and two included angles
of the quadrilateral TRUE are given,
i.e., TR = 3.5 cm, RU = 3 cm, UE = 4 cm,
R = 75° and U = 120°.
Steps of Construction:
(i) Draw a line segment RU = 3 cm.
(ii) At point R, make an XRU = 75°, and
cut an arc of length 3.5 cm from R, which
intersects RX at T.
(iii) At point U, make an RUY = 120° and
cut an arc of length 4 cm from U, which
intersects UY at E.
(iv) Join TE.
∴ TRUE is the required quadrilateral.
Question 25:
How will you construct a rectangle PQRS if you know only the lengths PQ and QR?
Answer:
Steps of Construction:
(i) Draw a line segment PQ of given length.
(ii) At Q, draw a ray QX such that PQX = 90°
(iii) From ray QX, cut QR of given length.
(iv) Through P, draw a ray PY parallel to QR.
(v) Through R, draw a ray RZ parallel to QP to meet the ray to step (iv) at S. Thus, PQRS is the required quadrilateral.
Question 26:
Construct the kite EASY if AY = 8 cm, EY = 4 cm and SY = 6 cm. Which properties of the kite did you use in the process?
Answer:
Steps of Construction:
Given AE = EY = 4 cm
AY = 8 cm
∴ AE + EY = AY = 8 cm
Which is not possible because the sum of the
length of any two sides of a triangle must be
greater than the third side.
∴ Kite EASY cannot be constructed.
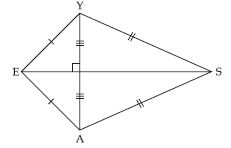
Question 27:
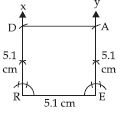
Construct a square READ with RE = 5.1 cm.
Answer:
Steps of Construction:
(i) Take a line segment RE = 5.1 cm.
(ii) At R draw XRE = 90 and at E draw YER
= 90.
(iii) From RX cut off RD = 5.1 cm and also from
EY cut off EA = 5.1 cm.
(iv) Join AD.
Then READ is the required square.
Question 28:
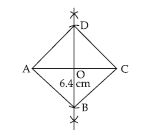
Construct a rhombus whose diagonals are 5.2 cm and 6.4 cm long.
Answer:
Steps of Construction:
(i) Draw AC = 6.4 cm
(ii) Construct the perpendicular bisector of AC. Let it meet AC at O.
(iii) Cut off
lengths of either side of the perpendicular bisector.
(iv) Join AB, BC, CD and DA. Then, ABCD is the required rhombus.
Question 29:
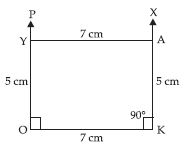
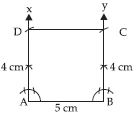
Construct a rectangle with adjacent sides of lengths 5 cm and 4 cm.
Answer:
Steps of Construction:
(i) Take a line segment AB = 5 cm.
(ii) At A, draw XAB = 90 and also at B draw
YBA = 90.
(iii) From AX, cut off
AD = 4 cm and also
from BY, cut off BC
= 4 cm.
(iv) Join DC.
Then ABCD is the the required rectangle.
Question 30:
Construct a parallelogram OKAY where OK = 5.5 cm and KA = 4.2 cm. It is unique?
Answer:
Construction of a || gm with two adjacent sides only is not possible because we need the measurement of included angle or any diagonal between the sides.