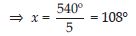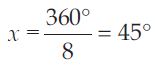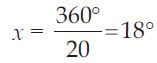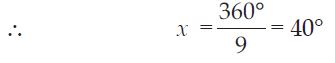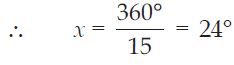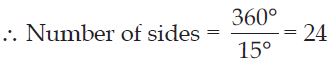Question 1:
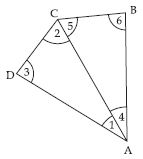
Take any quadrilateral, say ABCD shown in figure. Divide it into two triangle, by drawing a diagonal. You get six angles 1, 2, 3, 4, 5 and 6.
Use the angle sum property of a triangle and argue how the sum of the measures of A, B, C and D amounts to 180 + 180 = 360.
Answer:
A + B + C + D
= (1 + 4) + 6 + (5 + 2) + 3
= (3 + 1 + 2) + (4 + 6 + 5)
= 180 + 180 = 360 [By angle sum property of a triangle]
Question 2:
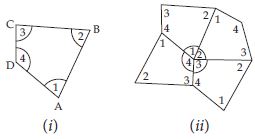
Take four congruent card-board copies of any quadrilateral ABCD, with angles as shown fig (i). Arrange the copies as shown in the figure, where angles 1 + 2 + 3 + 4 meet at a point as shown in fig. (ii)
What can you say about the sum of the angles 1, 2, 3 and 4?
Answer:
We know that, the sum of the angles 1, 2, 3 and 4 is 360.
The sum of the measure of the four angles of a quadrilateral is 360.
[Note: We denote the angles by 1, 2, 3, etc., and their respective measures by m1, m2, m3, etc.]
The sum of the measures of the four angles of a quadrilateral is 360.
Question 3:
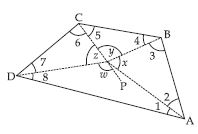
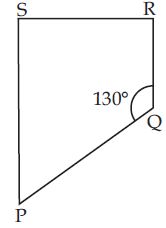
Take any quadrilateral ABCD shown in figure. Let P be any point in its interior. Join P to vertices A, B, C and D. In the figure, consider PAB. From this we see x = 180 – m2 – m3; similarly from PBC, y = 180 – m4 – m5, from PCD, z = 180 – m6 – m7 and from PDA, w = 180 – m8 – m1.
Use this to find the total measure m1 + m2 +… + m8, does it help to arrive at the result?
Remember: x + y + z + w = 360.
Answer:
Given that
x = 180 – m2 – m3 ...(i)
y = 180 – m4 – m5 ...(ii)
z = 180 – m6 – m7 ...(iii)
w = 180 – m8 – m1 ...(iv)
Adding equations (i), (ii), (iii) and (iv), we get
x + y + z + w = 720 – (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8)
360 = 720 – (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8)
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 720 – 360 = 360
A + B + C + D = 360
The sum of the measures of the four angles of a quadrilateral is 360.
Question 4:
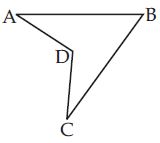
Consider quadrilateral ABCD. Split it into two triangles and find the sum of the interior angles shown in figure.
Answer:
The quadrilateral is concave.
Divide the quadrilateral ABCD into two triangles ABD and CBD.
In ABD, A + ABD + ADB = 180 ...(i)
and in BDC, C + CDB + DBC = 180 ...(ii)
Adding quations (i) and (ii), we get
A + ADB + ABD + C + CDB + DBC =
180 + 180 = 360
A + ADB + CDB + C + (CBD +
DBA) = 360
A + B + C + D = 360
Question 5:
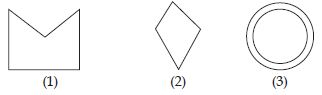
Given here are some figures:
Classify each of them on the basis of the
following:
(a) Simple curve
(b) Simple closed curve
(c) Polygon
(d) Convex polygon
(e) Concave polygon
Answer:
(a) (1), (2), (5), (6), (7)
(b) (1), (2), (5), (6), (7)
(c) (1), (2), (4)
(d) (2)
(e) (1), (4)
Question 6:
How many diagonals does each of the
following have:
(a) A convex quadrilateral
(b) A regular hexagon
(c) A triangle
Answer:
(a) A convex quadrilateral has 2 diagonals.
(b) A regular hexagon has 9 diagonals.
(c) A triangle has no diagonal.
Question 7:
What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex?
Answer:
360, Yes. (make a non-convex quadrilateral and try!)
Question 8:
Examine the table (Each figure is divided into triangles and the sum of the angles deduced from that?
What can you say about the angle sum of a convex polygon with number of sides?
(a) 7 (b) 8 (c) 10 (d) n
Answer:
(a) The angle sum of a convex polygon with 7 sides is given by:
(7 – 2) × 180 = 5 × 180 = 900
(b) The angle sum of a convex polygon with 8 sides is given by:
(8 – 2) × 180 = 6 × 180 = 1080
(c) The angle sum of a convex polygon with 10 sides is given by:
(10 – 2) × 180 = 8 × 180 = 1440
(d) The angle sum of a convex polygon with n sides is given by:
(n – 2) × 180.
Question 9:
What is a regular polygon?
State the name of a regular polygon of:
(i) 3 sides (ii) 4 sides (iii) 6 sides.
Answer:
Regular polygon: A regular polygon is both “equiangular” and “equilateral”.
(i) A regular polygon having 3 sides is called equilateral triangle.
(ii) A regular polygon having 4 sides is called square.
(iii) A regular polygon having 6 sides is called regular hexagon.
Question 10:
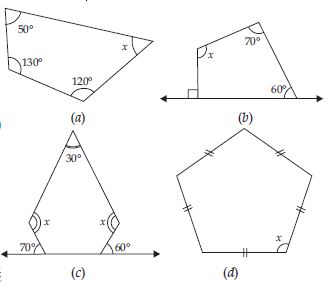
Find the angle measure x in the following figures:
Answer:
(a) 50 + 130 + 120 + x = 360
300 + x = 360
x = 360 – 300 = 60
(b) 90 + 60 + 70 + x = 360
220 + x = 360
x = 360 – 220 = 140
(c) Figure (c) has five sides:
its angle sum = (5 – 2) × 180
= 3 × 180 = 540
Also, exterior angles 70 and 60 are
given.
Corresponding interior angles are (180
– 70) = 110 and (180 – 60) = 120 respectively.
110 + 120 + x + 30 + x = 540
260 + 2x = 540
2x = 540 – 260
2x = 280
Figure (d) is a regular pentagon.
Its angle sum = (5 – 2) × 180
= 3 × 180 = 540
x + x + x + x + x = 540
5x = 540
Question 11:
Answer:
In the given figure:
Exterior angle x = (180 – 90) = 90
Exterior angle z = (180 – 30) = 150
As sum of interior angles of a triangle is 180.
90 + 30 + p = 180
120 + p = 180
p = 180 – 120 = 60
Exterior angle y = (180 – 60) = 120
x + y + z = 90 + 150 + 120
= 360.
Question 12:
Answer:
In the given figure:
Exterior angle x = (180 – 120) = 60
Exterior angle y = (180 – 80) = 100
Exterior angle z = (180 – 60) = 120
As sum of interior angles of a quadrilateral is
360.
120 + 80 + 60 + q = 360
260 + q = 360
q = 360 – 260
q = 100
Exterior angle w = (180 – 100)
= 80
x + y + z + w = 60 + 100 + 120 + 80
= 360
Question 13:
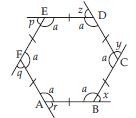
Take a regular hexagon.
What is the sum of measure of its exterior
angles x, y, z, p, q, r?
Answer:
Let ABCDEF is a regular hexagon having each side equal.
As the sum of the measures of the external angles of any polygon is 360.
x + y + z + p + q + r = 360
Question 14:
Take a regular hexagon.
Is x = y = z = p = q = r? Why?
Answer:
Yes, x = y = z = p = q = r, because the hexagon is regular.
Question 15:
Take a regular hexagon.
What is the measure of each exterior angle?
Answer:
The measure of each exterior angle is given
by x + x + x + x + x + x = 360
6x = 360
x = 60
Question 16:
Take a regular hexagon.
What is the measure of each interior angle?
Answer:
Measure of each interior angle
= 180– 60 = 120
Question 17:
Take a regular octagon.
What is the measure of each exterior and interior angle?
Answer:
The octagon being regular having 8 sides.
All the exterior angles have equal measure,
say x.
8x = 360
Measure of each exterior angle = 45
Measure of each interior angle = 180 – 45
= 135
Question 18:
Take a regular 20-gon.
What is the measure of each exterior and interior angle?
Answer:
The polygon being regular having 20 sides.
All the exterior angles have equal measure, say x.
20 x = 360
Measure of each exterior angle = 180
Measure of each interior angle = 180 – 18
= 162
Question 19:
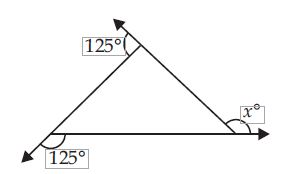
Find x in the following figures.
Answer:
As the sum of the measures of the external angles
of any polygon is 360.
125 + 125 + x = 360
250 + x = 360
x = 360 – 250 = 110
Question 20:
Find x in the following figures.
Answer:
As the sum of the measures of the external angles
of any polygon is 360.
x + 90 + 60 + 90 + 70 = 360
x + 310 = 360
x = 360 – 310
x = 50
Question 21:
Find the measure of each exterior angle of a regular polygon of 9 sides.
Answer:
The polygon being regular having 9 sides.
All the exterior angles have equal measure,
say x.
9x = 360
Measure of each exterior angle = 40
Question 22:
Find the measure of each exterior angle of a regular polygon of 15 sides.
Answer:
The polygon being regular having 15 sides.
All the exterior angles have equal measure,
say x.
15x = 360
Question 23:
How many sides does a regular polygon have if the measure of an exterior angle is 24?
Answer:
Total measure of all exterior angles = 360
Measure of each exterior angle = 24
The polygon has 15 sides.
Question 24:
How many sides does a regular polygon have if each of its interior angles is 165?
Answer:
Measure of each interior angle = 165
Measure of each exterior angle
= 180 – 165
= 15
Total measure of all exterior angles = 360
The polygon has 24 sides.
Question 25:
Is it possible to have a regular polygon with measure of each exterior angle as 22?
Answer:
No; since 22 is not a divisor of 360.
Question 26:
Can 22 be an interior angle of a regular polygon? Why?
Answer:
No; because each exterior angle is (180 – 22)
= 158, which is not a divisor of 360.
Question 27:
What is the minimum interior angle possible for a regular polygon? Why?
Answer:
The equilateral triangle being a regular polygon of 3 sides has the least measure of an interior angle is equal to 60.
Question 28:
What is the maximum exterior angle possible for a regular polygon?
Answer:
The equilateral triangle being a regular polygon of 3 sides has the least measure of an interior angle is equal to 60.
The greatest exterior angle of an equilateral triangle can be (180 – 60) = 120.
Question 29:
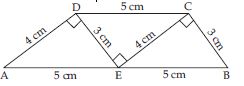
Take identical cut-outs of congruent triangles of sides 3 cm, 4 cm, 5 cm. Arrange them as shown figure.
You get a trapezium. (Check it!) Which are the parallel sides here? Should the non-parallel sides be equal?
Answer:
Quadrilateral DCEA,
DC = AE = 5 cm
and AD = EC = 4 cm
DC || AE AD || CE
DCEA is a parallelogram.
ABCD is a trapezium. Its parallel sides are AB and DC. Non-parallel sides are AD and CB.
Two more examples of trapeziums using the same set of triangles.
Question 30:
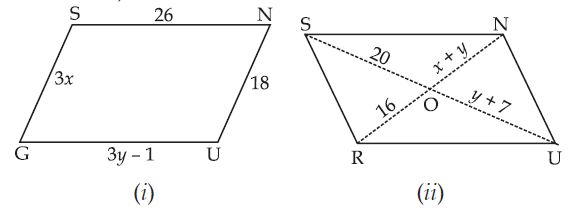
In a parallelogram mR = mN = 70, find m1 and mG.
Answer:
Question 31:
Answer:
Question 32:
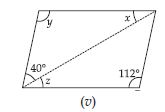
Consider the following parallelograms. Find the values of the unknown x, y, z.
Answer:
Question 33:
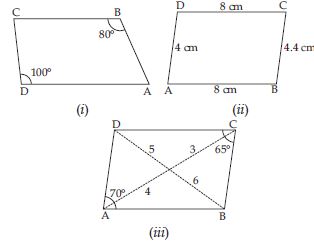
Can a quadrilateral ABCD be a parallelogramif
(i) D + B = 180
(ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
(iii) A = 70 and C = 65?
Answer:
Fig. (i) is not a parallelogram, because, the
opposite angles i.e., C and A are not equal.
Fig. (ii) is not a parallelogram, because, the
opposite sides i.e, AB and CD and BC and DA
are not equal.
Fig. (iii) is also not a parallelogram, because,
the diagonals of a parallelogram bisect each
other and here it is not so and A and C are
not equal.
Question 34:
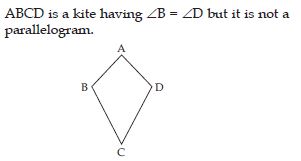
Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
Answer:
Question 35:
The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
Answer:
Question 36:
Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
Answer:
It is given that, ABCD is a parallelogram in which two adjacent angles A and B have
equal measure, say x.
mA = x and mB = x
Question 37:
The adjacent figure HOPE is a parallelogram.
Find the angle measures x, y and z. State the
properties you use to find them.
Answer:
Question 38:
The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm.)
Answer:
Question 39:
Answer:
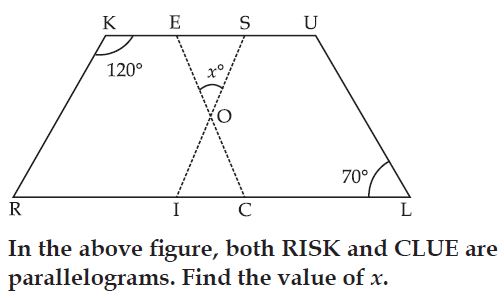
It is given that RISK and CLUE are parallelograms.
In parallelogram RISK;
RKS + ISK = 180 [Because, sum of any two
adjacent angles of a parallelogram is 180.]
120 + ISK = 180
ISK = 180 – 120 = 60
Also, in parallelogram CLUE,
CLU = CEU = 70
[Because, opposite angles of a parallelogram are
equal]
In OES; sum of three angles is equal to 180.
OES + ESO + x = 180
[ OES = CEU and ESO = ISK]
70 + 60 + x = 180
130 + x = 180
x = 180 – 130 = 50
Question 40:
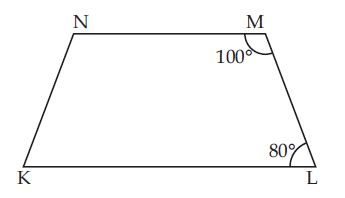
Explain how this figure is a trapezium. Which of its two sides are parallel?
Answer:
The given figure KLMN is a trapezium, as its two sides KL and MN are parallel, because, sum of its adjacent angles L and M is 180.
Question 41:
Find mC in the figure if AB || DC.
Answer:
It is given that, ABCD is a trapezium having
B = 120 and two of its sides AB and CD are
parallel.
B + C = 180
120 + C = 180
C = 180 – 120 = 60
Question 42:
Find the measure of P and S if SP || RQ in Fig. (If you find mR, is there more than one method to find mP?).
Answer:
It is given that, PQRS is a trapezium having Q =
130 and two of its sides PS and RQ are parallel.
P + Q = 180
P + 130 = 180
P = 50
Also, R and S each have measure 90.
We may find P by one more method.
i.e., Sum of all the interior angles of a quadrilateral
is 360.
P + Q + R + S = 360
P + 130 + 90 + 90 = 360
P + 310 = 360
P = 360 – 310
P = 50
Question 43:
Take a square sheet, say PQRS (Fig (i)). Fold along both the diagonals. Are their mid-point the same? Check if the angle at O is 90 by using a set-square.
This verifies the property stated above.
Answer:
Yes, their mid-point is the same and the angle
at O is 90.
We know that PQSR is a square whose diagonals
meet at O.
PO = OR (Since, the square is a parallelogram)
By SSS congruency condition, we see that
POQ SOR
[ PQ = SR; PO = OR; SO
= OQ]
mPOQ = mSOR
These angles being a linear
pair, each is right angle.
Question 44:
All rectangles are squares.
Answer:
FALSE
Question 45:
All rhombuses are parallelograms.
Answer:
TRUE
Question 46:
All squares are rhombuses and also rectangles.
Answer:
TRUE
Question 47:
All squares are not parallelograms.
Answer:
FALSE
Question 48:
All kites are rhombuses.
Answer:
FALSE
Question 49:
All rhombuses are kites.
Answer:
TRUE
Question 50:
All parallelograms are trapeziums.
Answer:
TRUE
Question 51:
All squares are trapeziums.
Answer:
TRUE
Question 52:
Identify all the quadrilaterals that have:
(a) Four sides of equal length
(b) Four right angles
Answer:
(a) Square and Rhombus
(b) Square and Rectangle
Question 53:
Explain how a square is:
(i) a quadrilateral
(ii) a parallelogram
(iii) a rhombus
(iv) a rectangle
Answer:
(i) Any four sided figure is called a quadrilateral and so is the square.
(ii) Opposite sides of a parallelogram are equal and parallel and so is in the square.
(iii) All the four sides of a rhombus are equal and so is in the square.
(iv) All the four angles of a rectangle are right angles and opposite sides are equal, same is the case with the square.
Question 54:
Name the quadrilaterals whose diagonals:
(i) bisect each other.
(ii) are perpendicular bisectors of each other.
(iii) are equal.
Answer:
(i) Parallelogram, Rhombus, Square, Rectangle
(ii) Rhombus, Square.
(iii) Rectangle, Square.
Question 55:
Explain why a rectangle is a convex quadrilateral.
Answer:
A rectangle is a convex quadrilateral, because no part of its diagonals lies in its exteriors.
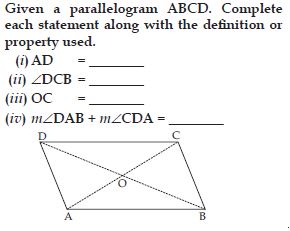
Question 56:
ABC is a right-angled triangle and O is the midpoint of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you).
Answer:
As DABC is a right-angled triangle, right-angled
at B. And O is the mid-point of AC.
Complete the rectangle ABCD as shown in the
adjoining figure.
Since, the diagonals of a rectangle are equal.
And all rectangles are parallelograms.
Also, diagonals of a parallelogram bisect each
other.
O is the mid-point of AC as well as BD.
O is equidistant from A, B, C and D as well.