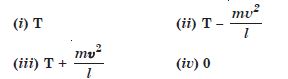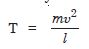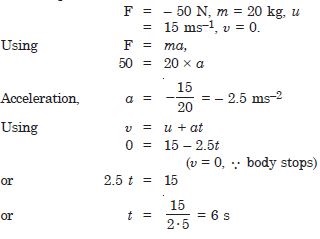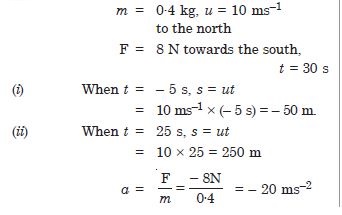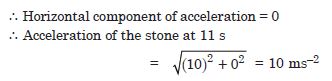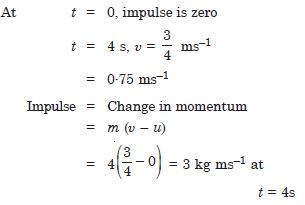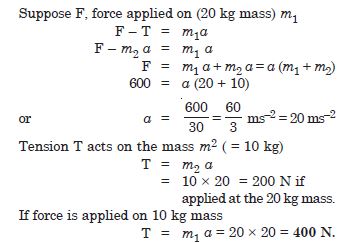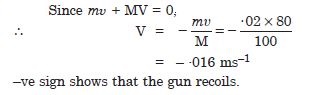Question 1:
Give the magnitude and direction of net force on :
a drop of rain falling down with a constant speed,
Answer:
Since drop of rain falls with a constant speed due to inertia of motion, therefore, no force acts on the rain drop.
Question 2:
Give the magnitude and direction of net force on :
a cork of mass 10 g floating on water,
Answer:
Due to inertia, cork of mass 10 g is floating on water, therefore no force acts on the cork.
Question 3:
Give the magnitude and direction of net force on :
a kite skilfully held stationary in the sky,
Answer:
The kite is held stationary in the sky due to its inertia of rest, therefore, no force acts on it.
Question 4:
Give the magnitude and direction of net force on :
a car moving with a constant velocity of 30 km h–1 on a rough road,
Answer:
No net force. The car is moving with a constant velocity of 30 km/h on a rough road due to its inertia of motion.
Question 5:
Give the magnitude and direction of net force on :
a high speed electron in space far from all gravitational objects and free of electric and
magnetic fields.
Answer:
No net force because it is far away from all material agencies producing electromagnetic and gravitational forces.
Question 6:
A pebble of mass 0.05 kg is thrown vertically upwards. Give the direction and magnitude of the net force on the pebble. during its upward motion,
Answer:
Mass of pebble = 0.05 kg
g = – 10 ms–2
Net force = mg = 0.05 kg × (– 10 ms–2)
= 0.5 N, acting vertically downwards
Question 7:
A pebble of mass 0.05 kg is thrown vertically upwards. Give the direction and magnitude of the net force on the pebble. during its downward motion,
Answer:
Net force = mg = 0.05 kg × (– 10 ms–2)
= 0.5 N acting vertically downwards
Question 8:
A pebble of mass 0.05 kg is thrown vertically upwards. Give the direction and magnitude of
the net force on the pebble.
at the highest point where it is momentarily at rest. Do your answer alter if the pebble
were thrown at an angle of say 45° with the horizontal direction ? Ignore air resistance
throughout.
Answer:
The stone is at rest at the highest point.
Therefore net force = mg = 0.05 kg × (– 10 ms–2)
= 0.5 N acting vertically downwards.
No, answers remain unaltered if pebble were thrown at angle of 45° with horizontal
direction.
The motion of the pebble is being affected by the downward pull of gravity (neglecting
effect of air) so that the velocity of the pebble at any instant has two components.
(i) the horizontal component which remains constant.
(ii) the vertical component. But these two components are independent of each other. So, our
answers do not alter.
Question 9:
Given the magnitude and direction of the net force acting on a stone of mass 0.1 kg
just after it is dropped from the window of a stationary train.
Answer:
m = 0·1 kg
a = g = 10 ms–2
Net force, F = mg = 0·1 × 10 N
= 1 N, vertically downward
Question 10:
Given the magnitude and direction of the net force acting on a stone of mass 0.1 kg just after it is dropped from the window of a train running at a constant velocity of 36 km h–1.
Answer:
Net force = 0·1 kg = 0·1 kg × 10 ms–2
= 1 N, vertically downward.
Question 11:
Given the magnitude and direction of the net force acting on a stone of mass 0.1 kg
just after it is dropped from the window of a train accelerating 1 ms–2.
Answer:
Net force = 0·1 kg × 10 ms–2
= 1 N, vertically downward
Acceleration of train has no vertical downward component.
Question 12:
Given the magnitude and direction of the net force acting on a stone of mass 0.1 kg lying on the floor of a train which is accelerating with 1 ms–2, the stone being at rest relative to the train. Neglect air resistance throughout.
Answer:
Net force = m × a
= 0·1 kg × 1 ms–2
= 0·1 N along the direction of the motion of the train.
Question 13:
One end of a string of length l is connected to a particle of mass m and the other to a small peg on a smooth horizontal table. If the particle moves in a circle with speed u the net force on the particle (directed towards the centre) is :
T is the tension in the string (Choose the correct alternative)
Answer:
T is correct.
The tension is acting towards the centre and along radius provides the necessary centripetal
force i.e.
Question 14:
A constant retarding force of 50 N is applied to a body of mass 20 kg moving initially with a speed of 15 ms–1. How long does the body take to stop ?
Answer:
Question 15:
A constant force acting on a body of mass 3 kg changes its speed from 2 ms–1 to 3.5 ms–1 in 25 s. The direction of the motion of the body remains unchanged. What is magnitude and direction of the force ?
Answer:
Question 16:
A body of mass 5 kg is acted upon by two perpendicular forces 8 N and 6 N. Give the magnitude and direction of the acceleration of the body.
Answer:
Question 17:
The driver of three-wheeler moving with a speed of 36 km h–1 sees a child standing in the middle of the road and brings his vehicle to rest in 4 s just in time to save the child. What is the average retarding force on the vehicle ? The mass of the three-wheeler is 400 kg and the mass of the driver is 65 kg.
Answer:
Question 18:
A rocket with a lift off mass 20,000 kg is blasted upwards with an initial acceleration of 5 ms–2 . Calculate the internal thrust (force) of the blast.
Answer:
Question 19:
A particle of mass 0·4 kg moving with a constant speed of 10 ms–1 to the north is subject to a constant force of 8 N directed towards the south for 30 s. Take the instant the force is applied to be t = 0, the position of the particle at that time to be x = 0, and predict its position at t = – 5 s, 25 s, 100 s.
Answer:
Question 20:
A truck starts from rest and accelerates uniformly with 2.0 ms–2. At t = 10 s, a stone is thrown by a person standing on the top of the truck (6 m high from the ground). What are the (a) velocity and (b) acceleration of the stone at t = 11 s ? (Neglect air resistance).
Answer:
Since the truck starts from rest, so initial velocity of stone is zero and the stone will possess horizontal velocity due to motion of truck and vertical downward velocity due to gravity.
Question 21:
A bob of mass 0·1 kg hung from ceiling of a room by a string 2 m long is set into
oscillation. The speed of the bob at its mean position is 1 ms–1. What is the
trajectory of the bob if the string is cut when the bob is :
at one of its extreme positions,
Answer:
m = 0·1 kg.
Since there is no horizontal component of the velocity at its extreme position, the only
acceleration on it is in vertically downward direction (due to force of gravity).
Hence the bob falls vertically downwards.
Question 22:
A bob of mass 0·1 kg hung from ceiling of a room by a string 2 m long is set into
oscillation. The speed of the bob at its mean position is 1 ms–1. What is the
trajectory of the bob if the string is cut when the bob is :
at its mean position ?
Answer:
The bob at its mean position is affected by the downward pull of gravity and its velocity in the horizontal direction. Therefore, it falls down along a parabolic path.
Question 23:
A man weighs 70 kg. He stands on a weighing scale in a lift which is moving ?
upwards with a uniform speed of 10 ms–1.
Answer:
Mass of man = 70 kg
Since speed is uniform, therefore
Acceleration, a = 0
R = mg = 70 × 10 = 700·0 N
Question 24:
A man weighs 70 kg. He stands on a weighing scale in a lift which is moving ?
downwards with a uniform acceleration of 5 m–2.
Answer:
a = 5 ms–2
mg – R = ma
or R = mg – ma
or = m (g – a)
or R = 70 (10 – 5) = 350 N
= 350·N, Reading is 35 kg
Question 25:
A man weighs 70 kg. He stands on a weighing scale in a lift which is moving ?
upwards with a uniform acceleration of 5 ms–2.
Answer:
R = mg + ma
= m (g + a)
= 70 (10 + 5) = 70 × 15
= 1050 N.
Reading is 105 kg
Question 26:
A man weighs 70 kg. He stands on a weighing scale in a lift which is moving ?
What would be the reading on the scale in each case ? What would be the reading if the lift
mechanism failed and is hurled down freely under gravity ?
Answer:
In case of free fall of the lift, a = g
then N = m (g – g) = 0
Hence, under the free fall the scale would read zero.
Question 27:
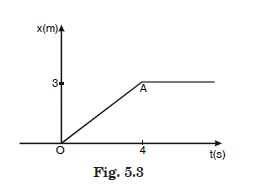
The Figure 5.3 shows the position-time graph of a particle of mass 4 kg. What is the :
Force on the particle for t < 0, t> 4s,
0 < t < 4 s ?
Answer:
At t < 0, Force on the particle=0
At t > 4s, no force acts on the particle as velocity is constant and acceleration is
zero.
As 0 < t < 4s. In this case, the velocity is uniform and hence there is no acceleration.
Therefore, force on the particle=0.
Question 28:
The Figure 5.3 shows the position-time graph of a particle of mass 4 kg. What is the :
Impulse at t = 0 and t = 4 s ; (Consider one-dimensional motion only).
Answer:
Question 29:
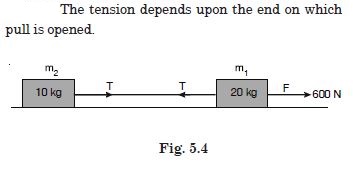
Two bodies of masses 10 kg and 20 kg respectively kept on a smooth, horizontal surface are tied to the ends of a light string, a horizontal force F = 600 N is applied at (i) A (ii) B along the direction of string. What is the tension in string in each case ?
Answer:
Question 30:
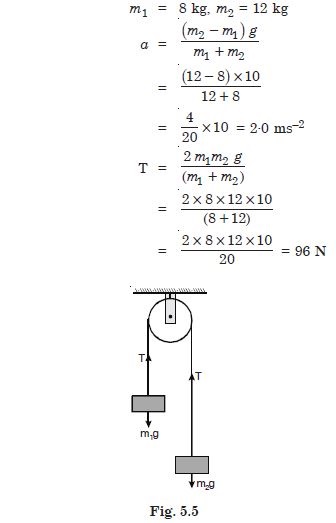
Two masses 8 kg and 12 kg are connected at the two ends of a light inextensible string that goes over a frictionless pulley. Find the acceleration of the masses, and the tension in the string when the masses are released.
Answer:
Question 31:
A nucleus is at rest in the laboratory frame of reference. Show that if it disintegrates into two smaller nuclei, the product must be emitted in opposite directions.
Answer:
Question 32:
Two billiard balls each of mass 0·05 kg and moving in opposite directions with speed of 6 ms–1 collide and rebound with the same speed. What is the impulse imparted to each ball due to the other ?
Answer:
Question 33:
A shell of mass 0·020 kg is fired by a gun of mass 100 kg. If the muzzle speed of the shell is 80 ms–1, what is the recoil of the gun ?
Answer:
Question 34:
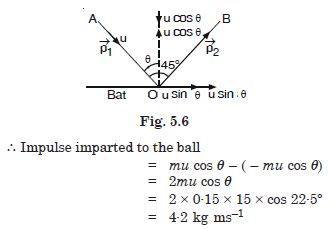
A batsman deflects a ball by an angle of 45° without changing its initial speed which is equal to 54 km h–1. What is the impulse imparted to the ball ? (Mass of the ball is 0·15 kg).
Answer:
Question 35:
stone of mass 0·25 kg tied to the end of a string is whirled round in a circle of radius 1·5 m with speed of 40 rev/min in a horizontal plane. What is the tension in the string ? What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N ?
Answer:
Question 36:
If in Q. 5·21 the speed of the stone is increased beyond the maximum permissible value, and the string breaks suddenly, which of the following correctly describes the trajectory of the stone after the string breaks :
- the stone moves radially outwards.
- the stone flies off tangentially from the instant the string breaks.
- the stone flies off at an angle with the tangent whose magnitude depends on the speed of the particle ?
Answer:
(b) the stone flies off tangentially from the instant the string breaks.
Question 37:
Explain why :
a horse cannot pull a cart and run in empty space ?
Answer:
In pulling the cart forward, the horse exerts force on the ground which gives reaction. The reaction of the earth may be resolved in two rectangular components. The horizontal component is responsible for the forward motion of the system as a whole. In the case of empty space the backward reaction is not possible. Hence the horse cannot pull the cart and run in empty space.
Question 38:
Explain why :
passengers are thrown forward from their seats when a speeding bus stops suddenly ?
Answer:
When a speeding bus stops suddenly, the passengers are thrown forward because due to inertia of motion the passengers tend to remain in their state of motion even though the bus has come to rest.
Question 39:
Explain why :
it is easier to pull a lawn mover than to push it ?
Answer:
Because in case of pull the roller becomes lighter in weight and due to decrease in normal reaction the force of friction decreases. While in case of push, normal reaction and hence force of friction increases. Hence it is easier to pull than to push a lawn roller.
Question 40:
Explain why :
a cricketer moves his hands backwards when holding a catch ?
Answer:
By doing so the cricket player increases the time and hence reduces the force exerted by the ball on his hands.