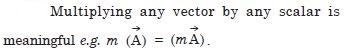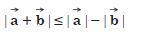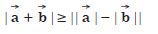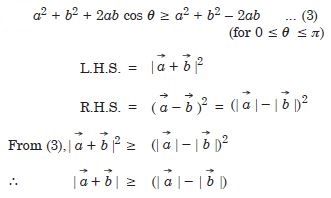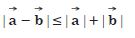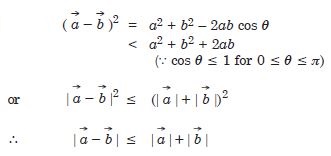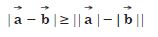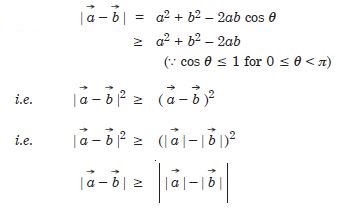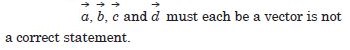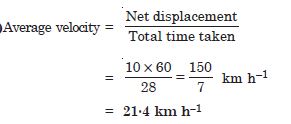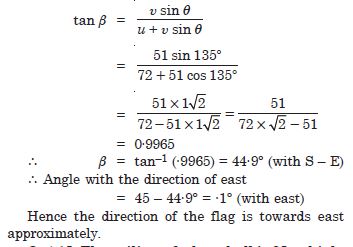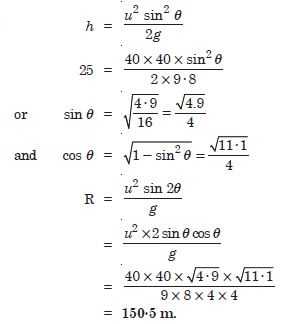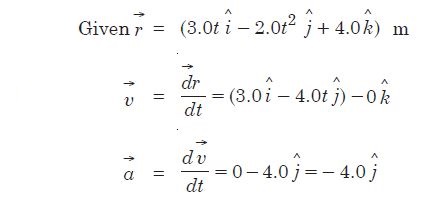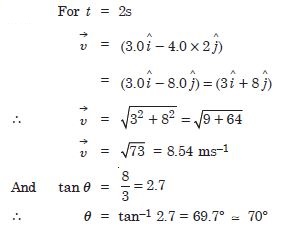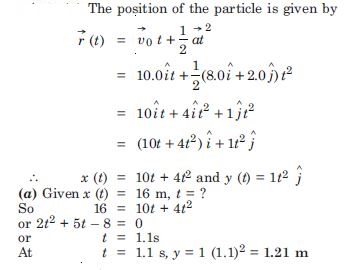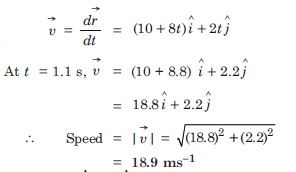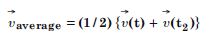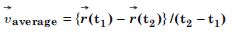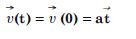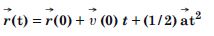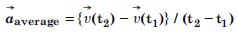Question 1:
State for each of the following physical quantities, if it is a scalar or a vector :
volume, mass, speed, acceleration, density, number of moles, velocity, angular velocity,
displacement and angular frequency.
Answer:
Scalars. Volume, mass, speed, density, number of moles, angular frequency.
Vectors. Acceleration, velocity, displacement, angular velocity.
Question 2:
Pick out the two scalar quantities in the following list :
Force, angular momentum, work, current, linear momentum, electric-field, average velocity,
magnetic moment, relative velocity.
Answer:
Work, current.
Question 3:
Pick out the only vector quantity in the following list :
Temperature, pressure, impulse, time, power, total path length, energy, gravitational
potential, coefficient of friction and charge.
Answer:
Impulse.
Question 4:
State with reasons, whether the following algebraic operations with scalars and vectors are
meaningful :
Adding any two scalars
Answer:
Adding any two scalars is not meaningful because they may not be of the same dimensions.
Question 5:
State with reasons, whether the following algebraic operations with scalars and vectors are
meaningful :
Adding a scalar to a vector of the same dimensions
Answer:
Adding a scalar to a vector of the same dimensions is not meaningful because scalar has no direction whereas vector has a direction.
Question 6:
State with reasons, whether the following algebraic operations with scalars and vectors are
meaningful :
Multiplying any vector by any scalar
Answer:
Question 7:
State with reasons, whether the following algebraic operations with scalars and vectors are
meaningful :
Multiplying any two scalars
Answer:
Multiplying any two scalars is meaningful.
Question 8:
State with reasons, whether the following algebraic operations with scalars and vectors are
meaningful :
Adding any two vectors
Answer:
Adding any two vectors is not meaningful because the vectors must be of the same nature.
Question 9:
State with reasons, whether the following algebraic operations with scalars and vectors are
meaningful :
Adding a component of a vector to the same vector.
Answer:
Adding a component of a vector to the same vector is meaningful.
Question 10:
Read each statement below carefully and state with reasons, if it is true or false :
the magnitude of a vector is always a scalar
Answer:
True, because, the magnitude of a vector is completely specified simply by its numerical value, which is a scalar.
Question 11:
Read each statement below carefully and state with reasons, if it is true or false :
each component of a vector is always a scalar
Answer:
False, because each component of a vector is always a vector.
Question 12:
Read each statement below carefully and state with reasons, if it is true or false :
the total path length is always equal to the magnitude of the displacement vector of a
particle
Answer:
False, because displacement has in general a magnitude which is not equal to the actual path length.
Question 13:
Read each statement below carefully and state with reasons, if it is true or false :
the average speed of a particle (defined a total path length divided by the time taken to
cover the path) is either greater than or equal to the magnitude of average velocity of the
particle over the same interval of time.
Answer:
True, because path length of actual path is either greater than or equal to displacement.
Question 14:
Read each statement below carefully and state with reasons, if it is true or false :
three vectors not lying in a plane can never add up to give null vector.
Answer:
True, because the resultant of two vectors is in the same plane as that of two vectors.
Question 15:
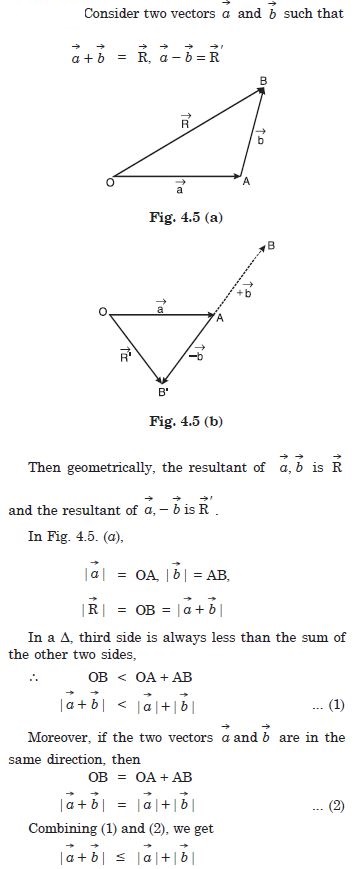
Establish the following vector inequalities geometrically or otherwise :
When does the equality sign in above cases apply ?
Answer:
Question 16:
Establish the following vector inequalities geometrically or otherwise :
When does the equality sign in above cases apply ?
Answer:
Question 17:
Establish the following vector inequalities geometrically or otherwise :
When does the equality sign in above cases apply ?
Answer:
Question 18:
Establish the following vector inequalities geometrically or otherwise :
When does the equality sign in above cases apply ?
Answer:
Question 19:
Answer:
Question 21:
Answer:
correct
Question 22:
Answer:
correct
Question 23:
Answer:
correct
Question 24:
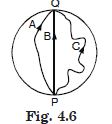
Three girls skating on a circular ice ground of radius 200 m start from a point P on the edge of the ground and reach a point Q diametrically opposite to P following different paths as shown in Fig. 4.6. What is the magnitude of the displacement vector for each girl ? For which girl is this equal to the actual length of path skated ?
Answer:
Magnitude of the displacement vector for each girl = diameter = 2 × 200 = 400 m.
This is equal to the actual length of the path skated for girl B.
Question 25:
A cyclist starts from the centre O of a circular park of radius 1 km, reaches the edge P of the park, then cycles along the circum-ference, and returns to the centre along QO as shown. If the round trip takes 10 min, what is the (a) net displacement (b) average velocity and (c) average speed of the cyclist ?
Answer:
Question 26:
On an open ground, a motorist follows a track that turns to his left by an angle of 60 after every 500 m. Starting from a given turn, specify the displacement of the motorist at the third, sixth and eighth turn. Compare the magnitude of the displacement with the total path length covered by the motorist in each case.
Answer:
Suppose the motorist starts from the point A and moves in the direction AB then along BC.
(i) Displacement at third turn x-component of displacement of the motorist at the third turn
Question 27:
A passenger arriving in a new town wishes to go from the station to a hotel located 10 km
away on a straight road from the station. A dishonest cabman takes him along a circuitous
path 23 km long and reaches the hotel in 28 minutes.
What is the average speed of the taxi
Answer:
Question 28:
A passenger arriving in a new town wishes to go from the station to a hotel located 10 km
away on a straight road from the station. A dishonest cabman takes him along a circuitous
path 23 km long and reaches the hotel in 28 minutes.
What is the magnitude of average velocity ? Are the two equal ?
Answer:
No, they are not always equal. The average speed equals average velocity’s magnitude only for a straight path.
Question 29:
Rain is falling vertically with a speed of 30 ms–1 . A woman rides a bicycle with a speed of 10 ms–1 in the north to south direction. What is the direction in which she should hold her umbrella ?
Answer:
The woman will direct the umbrella in a direction from which the rain appears to fall i.e. relative velocity of rain w.r.t. woman. Magnitude of relative velocity.
She should hold her umbrella at about 18 with the vertical, towards the south.
Question 30:
A man can swim with a speed of 4.0 km h–1 in still water. How long does he take to cross a river 1.0 km wide if the river flows steadily at 3.0 km h–1 and he makes his strokes normal to the river current ? How far down the river does he go when he reaches the other bank ?
Answer:
Question 31:
In a harbour, wind is blowing at the speed of 72 km h–1 and the flag on the mast of a boat anchored in the harbour flutters along the N-E direction. If the boat starts moving at a speed of 51 km h–1 to the north, what is the direction of the flag on the mast of the boat ?
Answer:
Since the flag flutters in the N-E direction, the wind must be flowing in the S-E direction. Therefore the angle between the wind velocity and the movement of the boat is 135. If b is the angle which the wind velocity makes with east direction, then using the relation
Question 32:
In a harbour, wind is blowing at the speed of 72 km h–1 and the flag on the mast of a boat anchored in the harbour flutters along the N-E direction. If the boat starts moving at a speed of 51 km h–1 to the north, what is the direction of the flag on the mast of the boat ?
Answer:
Since the flag flutters in the N-E direction, the wind must be flowing in the S-E direction. Therefore the angle between the wind velocity and the movement of the boat is 135. If b is the angle which the wind velocity makes with east direction, then using the relation
Question 33:
The ceiling of a long hall is 25 m high. What is the maximum horizontal distance that a ball thrown with a speed of 40 ms–1 can go without hitting the ceiling of the hall ?
Answer:
Question 34:
A cricketer can throw a ball to a maximum horizontal distance of 100 m. How much high above the ground can the cricketer throw the same ball ?
Answer:
Question 35:
A stone tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolutions in 25 s, what is the magnitude and direction of acceleration of the stone ?
Answer:
Question 36:
An aircraft executes a horizontal loop of radius 1.00 km with steady speed of 900 km h–1. Compare its centripetal acceleration with the acceleration due to gravity.
Answer:
Question 37:
Read the statement below carefully and state, with reasons, if it is true or false :
The net acceleration of a particle in circular motion is always along the radius of the
circle towards the centre.
Answer:
False. It is true only for uniform circular motion.
Question 38:
Read the statement below carefully and state, with reasons, if it is true or false :
The velocity vector of a particle at a point is always along the tangent to the path of the
particle at that point.
Answer:
True. Because while leaving the circular path, the particle moves tangentially to the circular path.
Question 39:
Read the statement below carefully and state, with reasons, if it is true or false :
The acceleration vector of a particle in uniform circular motion averaged over one cycle is
a null vector.
Answer:
True. Because it again comes to its original position.
Question 40:
Answer:
Question 41:
What is the magnitude and direction of velocity of the particle at t = 2s ?
Answer:
Question 42:
Answer:
Question 43:
What is the speed of the particle at that time ?
Answer:
Question 44:
Answer:
Question 45:
For any arbitrary motion in space, which of the following relations are true :
Answer:
It is not true because it holds for uniform acceleration.
Question 46:
For any arbitrary motion in space, which of the following relations are true :
Answer:
True because it is a general result.
Question 47:
For any arbitrary motion in space, which of the following relations are true :
Answer:
It is not true. It holds for uniform acceleration.
Question 48:
For any arbitrary motion in space, which of the following relations are true :
Answer:
It is not true.
Question 49:
For any arbitrary motion in space, which of the following relations are true :
Answer:
It is true because it is the general result.
Question 50:
Read each statement below carefully and state, with reasons and examples, if it is true or false : A scalar quantity is one that is conserved in a process
Answer:
False, because the scalar quantity may not be conserved, e.g., speed of a body may be variable.
Question 51:
Read each statement below carefully and state, with reasons and examples, if it is true or false : A scalar quantity is one that can never take negative values
Answer:
False, because scalars may have a – ve value, e.g., speed may be negative.
Question 52:
Read each statement below carefully and state, with reasons and examples, if it is true or false : A scalar quantity is one that must be dimensionless
Answer:
False, because a scalar may have dimension, e.g., speed has dimension [L1T: –1].
Question 53:
Read each statement below carefully and state, with reasons and examples, if it is true or false : A scalar quantity is one that does not vary from one point to another in space
Answer:
False, scalar may be variable e.g. speed.
Question 54:
Read each statement below carefully and state, with reasons and examples, if it is true or false : A scalar quantity is one that has the same value for observers with different orientations of axes.
Answer:
True, since a scalar does not have any orientation in space therefore, it has the same value with different orientations of axes.
Question 54:
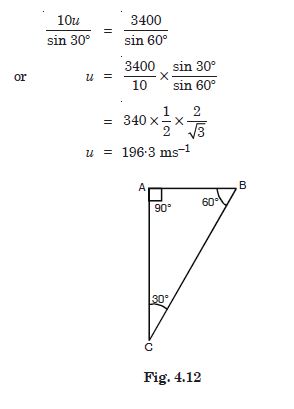
An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the aircraft positions 10.0 s apart is 30, what is the speed of the aircraft ?
Answer:
The distance, AC = 3400 m
The distance, AB = 10 u where u is the speed of the aircraft.