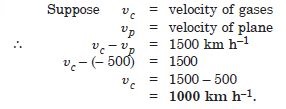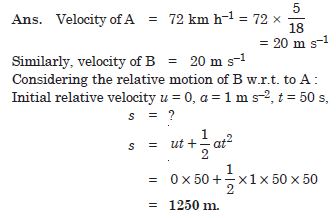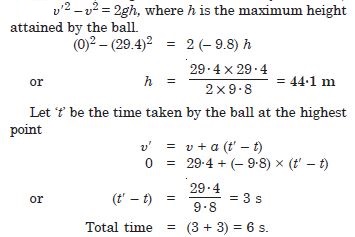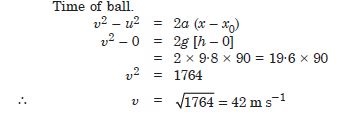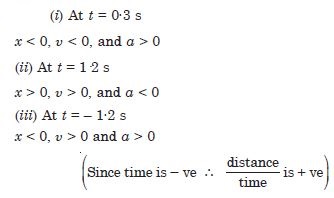Question 1:
In which of the following examples of motion can the body be considered approximately a point
object :
(a) a railway carriage moving without jerks between two stations,
(b) a monkey sitting on top of a man cycling smoothly on a circular track,
(c) a spinning cricket ball that turns sharply on hitting the ground,
(d) a tumbling beaker that has slipped off the edge of a table ?
Answer:
In (a), (b) the body can be considered approximately a point object because the motion of the object involves changes of position by distance much greater than its size.
Question 2:
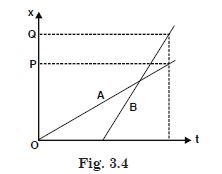
The position-time (x – t) graphs for two children A and B returning from their school O to
their homes P and Q respectively are shown in Fig. 3.4. Choose the correct entries in the
brackets below :
(A/B) lives closer to the school than (B/A).
Answer:
A lives closer to the school than B.
Question 3:
The position-time (x – t) graphs for two children A and B returning from their school O to
their homes P and Q respectively are shown in Fig. 3.4. Choose the correct entries in the
brackets below :
(A/B) starts from the school earlier than (B/A).
Answer:
A starts from the school earlier than B.
Question 4:
The position-time (x – t) graphs for two children A and B returning from their school O to
their homes P and Q respectively are shown in Fig. 3.4. Choose the correct entries in the
brackets below :
(A/B) walks faster than (B/A).
Answer:
B walks faster than A.
Question 5:
The position-time (x – t) graphs for two children A and B returning from their school O to
their homes P and Q respectively are shown in Fig. 3.4. Choose the correct entries in the
brackets below :
A and B reach home at the (same/ different) time.
Answer:
A and B reach home at the same time.
Question 6:
The position-time (x – t) graphs for two children A and B returning from their school O to
their homes P and Q respectively are shown in Fig. 3.4. Choose the correct entries in the
brackets below :
(A/B) overtakes (B/A) on the road (once/twice)
Answer:
B overtakes A on the road once.
Question 7:
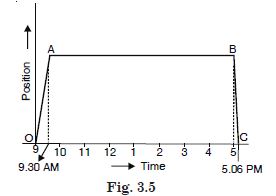
A woman starts from her home at
9·00 a.m., walks with a speed of 5 km h–1 on a straight road up to her office 2·5
km away, stays at the office upto 5·00 pm., and returns home by an auto with a speed of 25
km h–1. Choose suitable scales and plot the x – t graph of her motion.
Answer:
5 km distance is covered in 1 hour, so 2·5 km distance is covered in 2·5/5 = 0·5 hour and 25 km distance is covered in 1 hour so 2·5 km distance is covered in 1/10 hour i.e. 6 minutes. Moreover, as the velocity becomes zero at A, there must be a ‘speeding down’. Therefore the (x – t) graph must be curved. Similarly, the curves at O, B, C must be slightly curved.
Question 8:
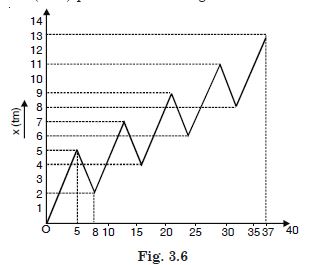
A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1s. Plot the x – t graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start.
Answer:
Effective increase in position co-ordinates in 8 s
= 5 m – 3 m = 2 m
2 metre distance is travelled by the drunkard in 8 s.
8 metre distance is travelled by the drunkard in
Now after 32 s, when the drunkard takes next 5 steps forward there will be the position of
the pit in to which he falls.
Total time taken by drunkard to fall in the pit
= 32 + 5 = 37 s
The (x – t) plot is shown in Fig.
Question 9:
A jet air plane travelling at the speed of 500 km h: –1 ejects its products of combustion at the speed of 1500 km h: –1 relative to the jet plane. What is the speed of the latter with respect to an observer on the ground ?
Answer:
Question 10:
A car moving along a straight highway with a speed of 126 km h–1 is brought to a stop within a distance of 200 m. What is the retardation of the car (assumed uniform), and how long does it take for the car to stop ?
Answer:
Question 11:
Two trains A and B of length 400 m each are moving on two parallel tracks with a uniform speed of 72 km h–1 in the same direction, with A ahead of B. The driver of B decides to overtake A and accelerates by 1 m s–2. If after 50 s, the guard of B just brushes past the driver of A, what was the original distance between them ?
Answer:
Question 12:
On a two-lane road, car A is travelling with a speed of 36 km h–1. Two cars B and C approach car A in opposite direction with a speed of 54 km h–1 each. At a certain instant, when the distance AB is equal to AC, both being 1 km, B decides to overtake A before C does. What minimum acceleration of car B is required to avoid an accident ?
Answer:
Question 13:
Two towns A and B are connected by a regular bus service with a bus leaving in either direction every T minutes. A man cycling with a speed of 20 km h–1 in the direction A to B notices that a bus goes past him every 18 min in the direction of his motion and every 6 min in the opposite direction. What is the period T of the bus service and with what speed (assumed constant) do the buses ply on the road ?
Answer:
Question 14:
A player throws a ball upwards with an initial speed of 29·4 m s–1.
What is the direction of acceleration during the upward motion of the ball ?
Answer:
Direction of acceleration during the upward motion of ball is vertically downward.
Question 15:
A player throws a ball upwards with an initial speed of 29·4 m s–1.
What are the velocity and acceleration of the ball at the highest point of its motion ?
Answer:
Velocity at the highest point of its motion = 0.
Acceleration of the ball at the highest point of its motion = 9·8 m s–2 vertically downward.
Question 16:
A player throws a ball upwards with an initial speed of 29·4 m s–1.
Choose x = 0 and t = 0 to be the location and time of the ball at its highest point,
vertically downwards direction to be the positive direction of x-axis, and give the signs of
position, velocity and acceleration of the ball during its upward and downward motion.
Answer:
Question 17:
A player throws a ball upwards with an initial speed of 29·4 m s–1.
To what height does the ball rise and after how long does the ball return to the player’s
hands ? (Take g = 9.8 m s–2, and neglect air resistance).
Answer:
Question 18:
Read each statement below carefully and state with reasons and examples, if it is true or
false : A particle in one dimensional motion :
with zero speed at an instant may have non-zero acceleration at that instant,
Answer:
True.
When a body is projected upward at the highest point, velocity = 0, acceleration 0.
Question 19:
Read each statement below carefully and state with reasons and examples, if it is true or
false : A particle in one dimensional motion :
with zero speed may have non-zero velocity.
Answer:
False. In this case magnitude of velocity
= speed, which is not zero.
Question 20:
Read each statement below carefully and state with reasons and examples, if it is true or
false : A particle in one dimensional motion :
with constant speed must have zero acceleration.
Answer:
True. Velocity will be constant acceleration = 0 (if the particle rebounds instantly with the same speed, it implies infinite acceleration which is unphysical, speed does not change).
Question 21:
Read each statement below carefully and state with reasons and examples, if it is true or
false : A particle in one dimensional motion :
with positive value of acceleration must be speeding up.
Answer:
False. (true only when the chosen positive direction is along the direction of motion).
Question 22:
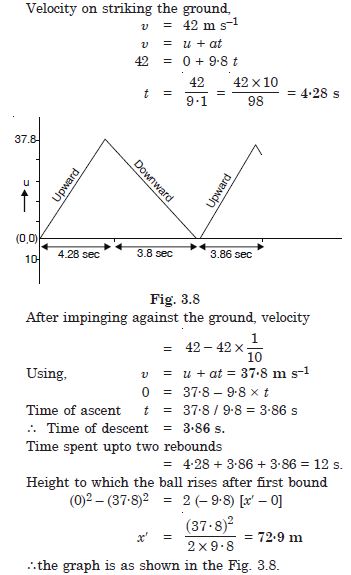
A ball is dropped from a height of 90 m on a floor. At each collision with the floor, the ball loses one-tenth of its speed. Plot the speed-time graph of its motion between t = 0 to 12 s.
Answer:
Question 23:
Explain clearly, with examples, the distinction between :
(a) magnitude of displacement (sometimes called distance) over an interval of time, and the
total length of path covered by a particle over the same interval.
Answer:
Displacement is the difference of final position co-ordinate and initial co-ordinate. It is a
vector quantity. When a body changes its position, the straight line joining the initial and
final positions of a body in the direction from initial to final positions is called its
displacement, irrespective of the nature of the actual path taken by the body.
Distance is the total length of the path travelled by a body in a certain interval of time.
Question 24:
Explain clearly, with examples, the distinction between :
(b) magnitude of average velocity over an interval of time, and the average speed over the
same interval [Average speed of a particle over an interval of time is defined as the total
path length divided by the time interval]. Show in both (a) and (b) that the second quantity
is either greater than or equal to the first. When is the equality sign true ? (For
simplicity, consider one dimensional motion only.)
Answer:
Question 25:
A man walks on a straight road from his home to a market 2·5 km away with a speed of 5 km
h–1. Finding the market closed, he instantly turns and walks back home with a
speed of 7·5 km h–1. What is the
(a) magnitude of average velocity and
(b) average speed of the man over the interval of time
(i) 0 to 30 min. (ii) 0 to 50 min. (iii) 0 to 40 min. ?
Answer:
Question 26:
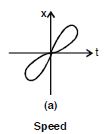
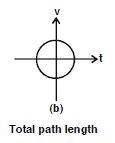
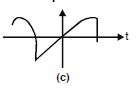
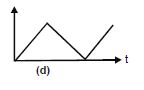
Look at the graphs (a) to (d) in Fig. carefully and state with reasons, which of these cannot possibly represent one dimensional motion of a particle.
Answer:
A particle cannot have two different positions at the same time.
Question 27:
Look at the graphs (a) to (d) in Fig. carefully and state with reasons, which of these cannot possibly represent one dimensional motion of a particle.
Answer:
A particle cannot have velocity in opposite directions at the same time.
Question 28:
Look at the graphs (a) to (d) in Fig. carefully and state with reasons, which of these cannot possibly represent one dimensional motion of a particle.
Answer:
Speed is always non-negative, so this is impossible.
Question 29:
Look at the graphs (a) to (d) in Fig. carefully and state with reasons, which of these cannot possibly represent one dimensional motion of a particle.
Answer:
Total path length of a particle can never decrease with time.
Therefore all the four graphs are impossible.
It may be noted that the arrows in the graphs are meaningless.
Question 30:
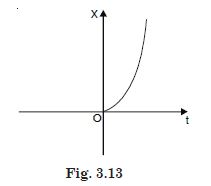
Figure 3.13 shows x – t plot of one dimensional motion of a particle. Is it correct to say from the graph that the particle moves in a straight line for t < 0 and on a parabolic path for t> 0 ? If not, suggest a suitable physical context for this graph.
Answer:
No. Wrong, x – t plot does not show the trajectory of a particle.
For t < 0, x=0
There is no motion at all.
For t > 0, the velocity is non-uniform but the motion may be along a straight line.
Context. A body is dropped from a tower (x = 0) at t = 0.
Since the motion is uniformly accelerated, the displacement varies parabolically with
time.
This graph can be of a particle being dropped from a certain height.
Question 31:
A police van moving on a highway with a speed of 30 km h–1 fires a bullet at a thief’s car speeding away in the same direction with a speed of 192 km h–1. If the muzzle speed of the bullet is 150 ms–1, with what speed does the bullet hit the thief’s car ? (Note : Obtain the speed which is relevant for damaging the thief’s car.)
Answer:
Question 32:
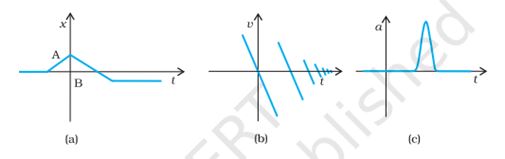
Suggest a suitable physical situation for each of the following graphs : (Fig 3.22).
Answer:
(a)
A ball at rest on a smooth floor is kicked,
it rebounds from a wall with reduced speed and moves
to the opposite wall which stops it.
rebounding from the floor with reduced speed after each hit.
hitting it with a bat for a very short time interval.
Question 33:
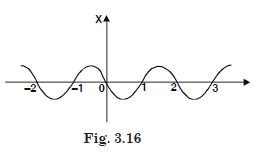
Figure 3.16 gives the (x–t) plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0·3 s, 1·2 s, – 1·2 s.
Answer:
Question 34:
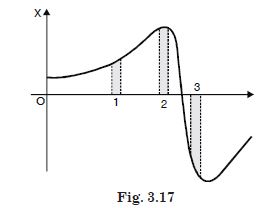
Figure 3.17 give the x-t plot of a particle in one dimensional motion. Three different equal
intervals of time are shown. In which interval is the average speed greatest and in which is
it the least ?
Give the sign of average velocity for each interval.
Answer:
Average speed is greatest in 3, because slope is greatest there. Sign of displacement is
neglected.
Average speed is the least in 2, because slope is least there.
(i) u > 0 in 1 (Distance increasing)
(ii) u > 0 in 2 (Distance increasing)
(iii) u < 0 in 3 (Distance decreasing).
Question 35:
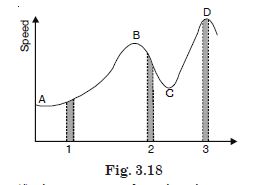
Figure 3.18 gives a speed-time graph of a particle in motion along a constant direction. Three equal intervals of time are shown. In which interval is the average acceleration greatest in magnitude ? In which interval is the average speed greatest ? Choosing the positive direction as the constant direction of motion, give the signs of u and a in the three intervals. What are the accelerations at the points A, B, C and D ?
Answer:
(i) Average acceleration is greatest in magnitude in 2 because the change of velocity is more
in the same time interval.
(ii) Average speed is greatest in 3, because speed is higher than any other interval 1 or
2.
(iii) u > 0 in 1, 2 and 3
a > 0 in 1 and 3, a < 0 in 2
a = 0 at the points A, B, C and D because there is instantaneous no change in speed.