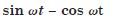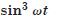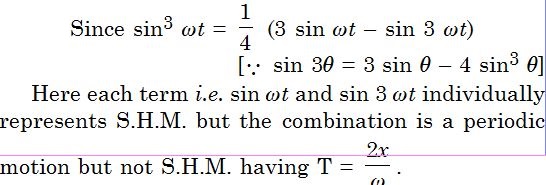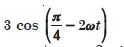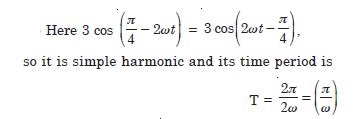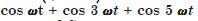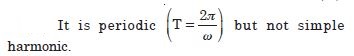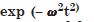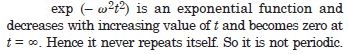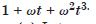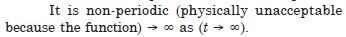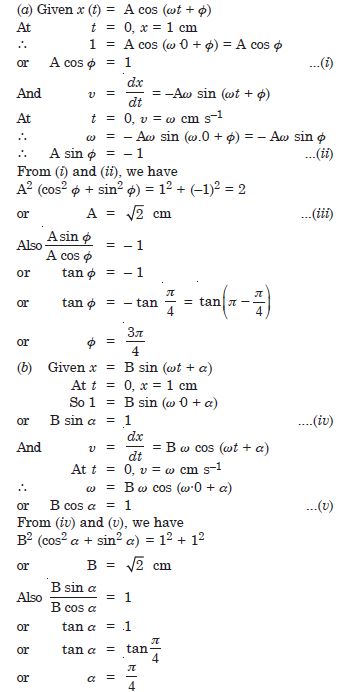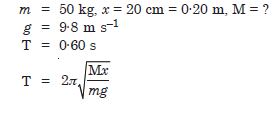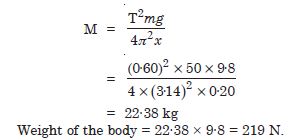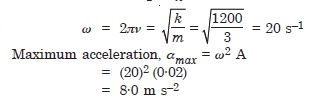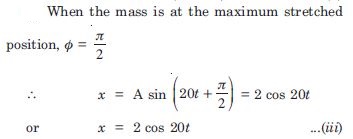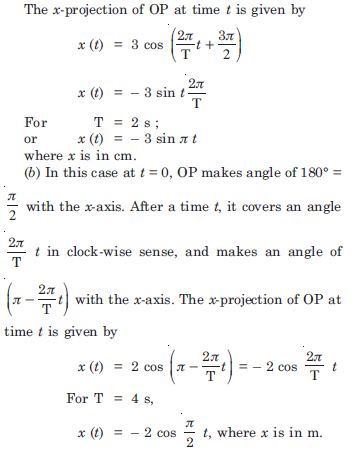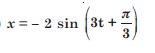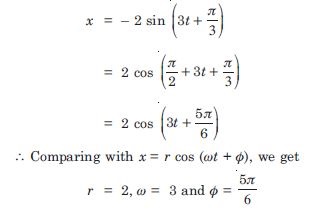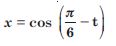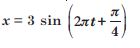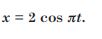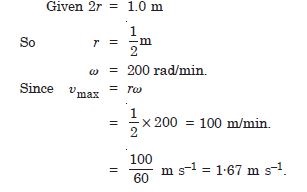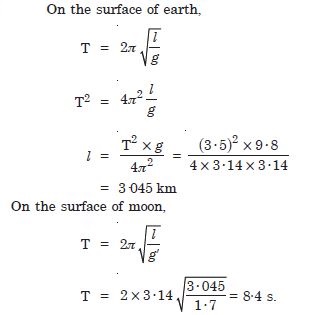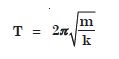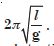Question 1:
Which of the following examples represent periodic motion ?
- A swimmer completing one (return) trip from one bank of a river to the other and back.
- A freely suspended bar magnet displaced from its N-S direction and released
- A hydrogen molecule rotating about its centre of mass.
- An arrow released from a bow
Answer:
Options 2 and 3
Question 2:
Which of the following examples represent (nearly) simple harmonic motion, and which
represents periodic but not simple harmonic motion :
The rotation of the earth about its axis.
Answer:
The rotation of the earth about its axis represents periodic but not S.H.M.
Question 3:
Which of the following examples represent (nearly) simple harmonic motion, and which
represents periodic but not simple harmonic motion :
The motion of an oscillatory mercury column in a U-tube.
Answer:
The motion of an oscillatory mercury column in a U-tube is S.H.M.
Question 4:
Which of the following examples represent (nearly) simple harmonic motion, and which
represents periodic but not simple harmonic motion :
The motion of a ball-bearing inside a smooth curved bowl, when released from a point
slightly above the lowermost position.
Answer:
The motion of a ball-bearing inside a smooth curved bowl when released from a point slightly above the lowermost position represent S.H.M.
Question 5:
Which of the following examples represent (nearly) simple harmonic motion, and which
represents periodic but not simple harmonic motion :
General vibration of a polyatomic molecule about its equilibrium configuration position.
Answer:
A polyatomic molecule has a number of natural frequencies, so in general, its vibration is a superposition of S.H.M’s of a number of different frequencies. The superposition is periodic but not S.H.M.
Question 6:
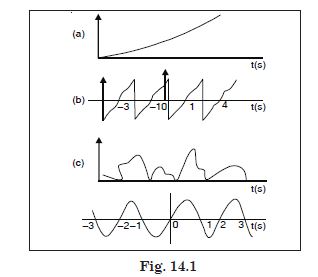
Given below are x–t plots for linear motion of a particle. Which of the plots represent periodic motion ? What is the period of motion (in case of periodic motion) ?
Answer:
It is not periodic.
It is periodic with a period = 2 s
It is not periodic. Repetition of merely one portion is not enough for periodic motion. The
entire motion during one period should be repeated successively.
It is periodic with a period = 2 s.
Question 7:
Which of the following functions of time represent : (a) simple harmonic,
(b) periodic but not simple harmonic, and (c) non-periodic motion ? Give the period for each
case of periodic motion : (w is any positive constant).
Answer:
Question 8:
Which of the following functions of time represent : (a) simple harmonic,
(b) periodic but not simple harmonic, and (c) non-periodic motion ? Give the period for each
case of periodic motion : (w is any positive constant).
Answer:
Question 9:
Which of the following functions of time represent : (a) simple harmonic,
(b) periodic but not simple harmonic, and (c) non-periodic motion ? Give the period for each
case of periodic motion : (w is any positive constant).
Answer:
Question 10:
Which of the following functions of time represent : (a) simple harmonic,
(b) periodic but not simple harmonic, and (c) non-periodic motion ? Give the period for each
case of periodic motion : (w is any positive constant).
Answer:
Question 11:
Which of the following functions of time represent : (a) simple harmonic,
(b) periodic but not simple harmonic, and (c) non-periodic motion ? Give the period for each
case of periodic motion : (w is any positive constant).
Answer:
Question 12:
Which of the following functions of time represent : (a) simple harmonic,
(b) periodic but not simple harmonic, and (c) non-periodic motion ? Give the period for each
case of periodic motion : (w is any positive constant).
Answer:
Question 13:
A particle is in linear simple harmonic motion between two points A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is at the end A
Answer:
At the end A 0, +, +
Question 14:
A particle is in linear simple harmonic motion between two points A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is at the end B
Answer:
At the end BO, –, –
Question 15:
A particle is in linear simple harmonic motion between two points A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is at the mid-point of AB going towards A.
Answer:
at the mid-point of AB going towards A –, 0, 0
Question 16:
A particle is in linear simple harmonic motion between two points A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is at 2 cm away from B going towards A.
Answer:
at 2 cm away from B going towards A – , – , –
Question 17:
A particle is in linear simple harmonic motion between two points A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is at 3 cm away from A going towards B and
Answer:
at 3 cm away from A going towards B +, +, +
Question 18:
A particle is in linear simple harmonic motion between two points A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is at 4 cm away from A going towards A.
Answer:
at 4 cm away from A going towards A (–, –, –)
(Here 0 stands for the magnitude of the quantity)
Question 19:
Which of the following relationship between the acceleration a and the displacement x of a
particle involves simple harmonic motion :
- a = 0.7 x
- a = – 200x2
- a = – 10x
- a = 100x2
Answer:
For a simple harmonic motion acceleration = – (constant) displacement
Answer (b) is correct.
Question 20:
Answer:
Question 21:
A spring balance has a scale that reads 0 to 50 kg. The length of the scale is 20 cm. A body suspended from this balance, when displaced and released, oscillates with a period of 0·6 s. What is the weight of the body ?
Answer:
Question 22:
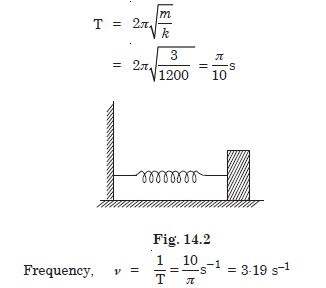
A spring of force constant 1200 Nm–1 is mounted on a horizontal table as shown in Fig. 14.2. A mass of 3·0 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2·0 cm and released. Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
Answer:
Question 23:
In exercise 14.9, let us take the position of mass when the spring is unstretched as x = 0 , and the direction from left to right as the positive direction of x-axis. Given x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t = 0), the mass is at the mean position
Answer:
Question 24:
In exercise 14.9, let us take the position of mass when the spring is unstretched as x = 0 , and the direction from left to right as the positive direction of x-axis. Given x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t = 0), the mass is at the maximum stretched position, and
Answer:
Question 25:
In exercise 14.9, let us take the position of mass when the spring is unstretched as x = 0 ,
and the direction from left to right as the positive direction of x-axis. Given x as a
function of time t for the oscillating mass if at the moment we start the stopwatch (t = 0),
the mass is
at the maximum compressed position.
In what way do these functions for SHM differ from each other, in frequency, in amplitude or
the initial phase ?
Answer:
Question 26:
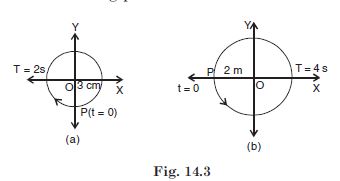
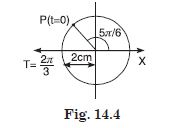
Figure 14.3 below correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the period of revolution (i.e. clockwise or anticlockwise) are indicated on each figure. Obtain the corresponding simple harmonic motion of the x-projection of the radius vector of the revolving particle P in each case.
Answer:
Question 27:
Plot the corresponding reference circle for each of the following S.H.M. Indicate the initial t = 0 position of the particle, the radius of circle and angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to the anticlockwise in every case : (x is in cm and t is in s)
Answer:
Question 28:
Plot the corresponding reference circle for each of the following S.H.M. Indicate the initial t = 0 position of the particle, the radius of circle and angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to the anticlockwise in every case : (x is in cm and t is in s)
Answer:
Question 29:
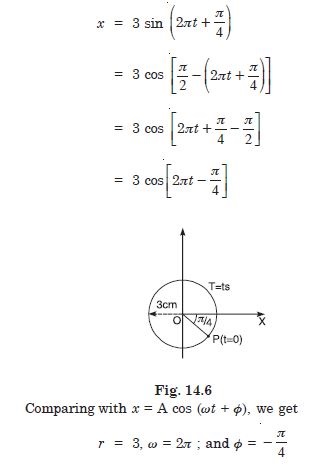
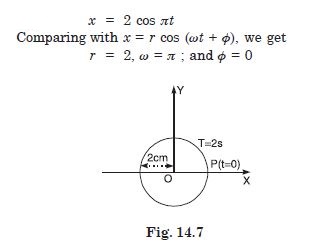
Plot the corresponding reference circle for each of the following S.H.M. Indicate the initial t = 0 position of the particle, the radius of circle and angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to the anticlockwise in every case : (x is in cm and t is in s)
Answer:
Question 30:
Plot the corresponding reference circle for each of the following S.H.M. Indicate the initial t = 0 position of the particle, the radius of circle and angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to the anticlockwise in every case : (x is in cm and t is in s)
Answer:
Question 31:
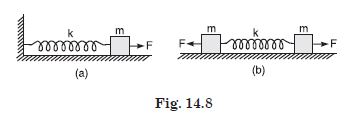
Figure 14.8 (a) shows a spring of force constant k clamped rigidly at one end and a mass m
attached to its free end stretches the spring. Figure 14.8 (b) shows these same spring with
both ends free and attached to a mass m at either end. Each end of the spring in figure 14.8
(b) is stretched by the same force F.
(i) What is the maximum extension of the spring in the two cases ?
(ii) If the mass in (a) and the two masses in (b) are released free, what is the period of
oscillation in each case ?
Answer:
Question 32:
The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0 m. If the piston moves with simple harmonic motion with angular frequency of 200 rad/min. What is its minimum speed ?
Answer:
Question 33:
The acceleration due to gravity on the surface of the moon 1·7 m s–2. What is the time period of a simple pendulum on the surface of moon if time-period on the surface of earth is 3·5 s ? (g on the surface of earth = 9·8 m s–2)
Answer:
Question 34:
Answer the following question :
Time period of a particle in S.H.M. depends on the constant k and mass m of the particle ;
A simple pendulum executes S.H.M. approximately. Why then is the time period of a pendulum independent of the mass of the pendulum ?
Answer:
For a simple pendulum, k itself is proportional to m, therefore m cancels out. Hence the time period of a pendulum is independent of the mass of the pendulum.
Question 35:
Answer the following question :
The motion of a simple pendulum is approximately simple harmonic for small angles of
oscillation. For larger angles of oscillation, a more involved analysis shows that T is
greater than
Think of a qualitative argument to appreciate this result.
Answer:
Question 36:
Answer the following question :
A man with a wrist watch on his hand falls from the top of a tower. Does the watch give
correct time during the free fall ?
Answer:
Yes, the watch gives correct time during the free fall because the wrist watch depends on spring action and has nothing to do with gravity.
Question 37:
Answer the following question :
What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely
falling under gravity ?
Answer:
Gravity disappears for a man under free fall. Therefore frequency is zero.
Question 38:
A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed . If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period ?
Answer:
Question 39:
Answer:
Question 40:
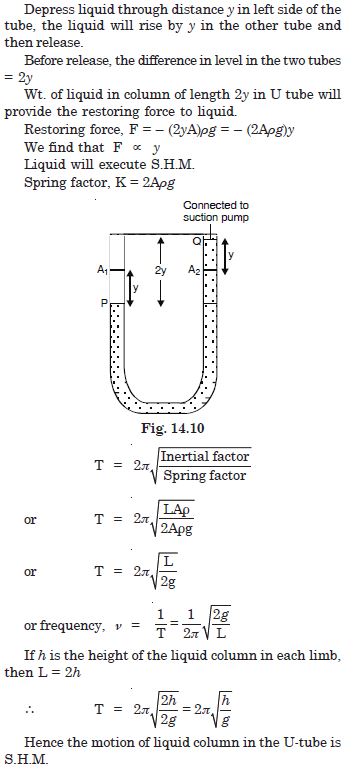
One end of a U-tube containing mercury is connected to a suction pump and the other end is open to the atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the liquid column in the U-tube executes simple harmonic motion.