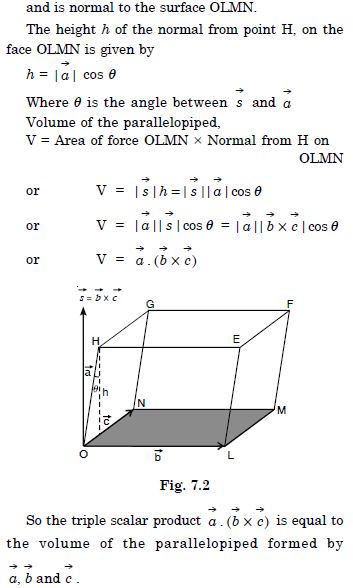
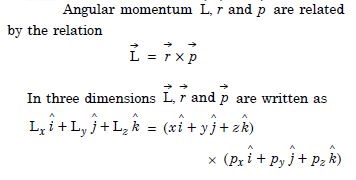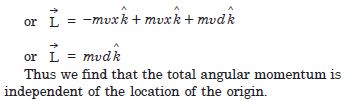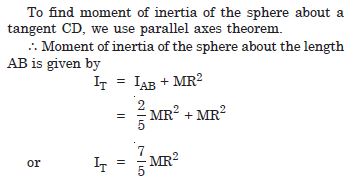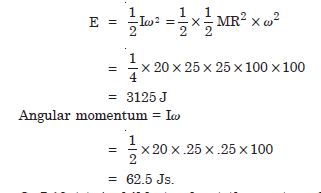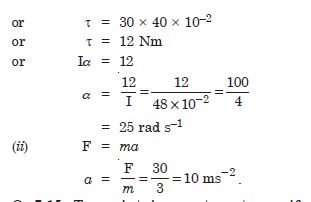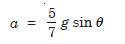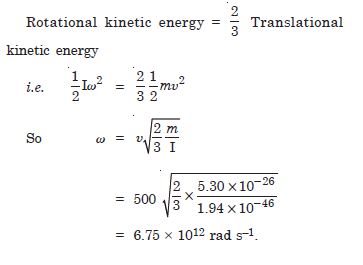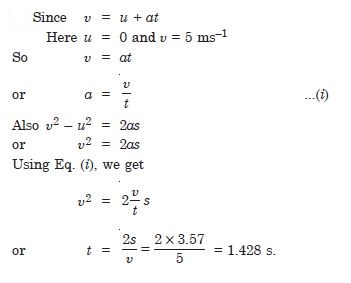Question 1:
Give the location of the centre of mass of a sphere
Answer:
The geometrical centre
Question 2:
Give the location of the centre of mass of a cylinder
Answer:
The geometrical centre
Question 3:
Give the location of the centre of mass of a ring
Answer:
The geometrical centre
Question 4:
Give the location of the centre of mass of a cube, each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body ?
Answer:
The geometrical centre
The centre of mass of a body does not necessarily lie inside the body.
The centre of mass may lie outside the body, as in case of a ring, a hollow sphere, a hollow
cylinder, a hollow cube etc.
Question 5:
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Å (1 Å = 10–10 m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.
Answer:
Question 6:
A child sits stationary at one end of a long trolley moving uniformly with a speed on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of the cm of the (trolley + child) system ?
Answer:
The speed of the cm of the (trolley + child) system remains unchanged (equal to ) because no external force acts on the system. The forces involved in running on the trolley are internal to this system.
Question 7:
Answer:
Question 8:
Answer:
Question 9:
Answer:
Question 10:
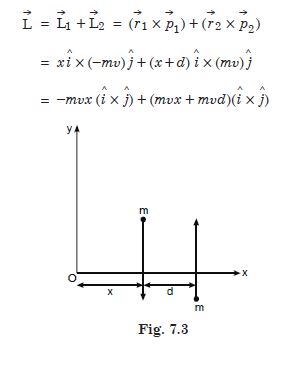
Two particles each of mass m and velocity u travel in opposite directions along parallel lines separated by a distance d. Show that the vector angular momentum of the two particle system is the same whatever be the point about which the angular momentum is taken.
Answer:
Let us consider a special case in which the two particles travel parallel to y-axis as shown
in the figure.
The total angular momentum of the particles m and m is given by
Question 11:
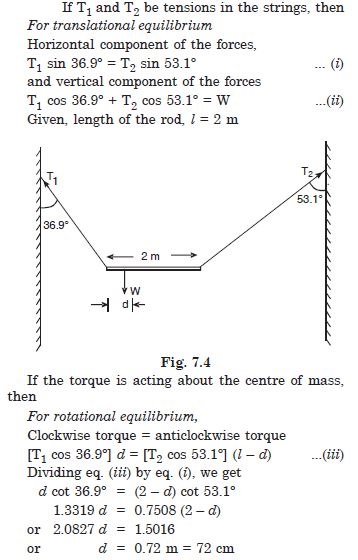
A non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in the figure. The angles made by the strings with the vertical are 36.9 and 53.1 respectively. The bar is 2 m long. Calculate the distance d of the centre of gravity of the bar from its left end.
Answer:
Question 12:
A car weighs 1800 kg. The distance between its front and back axles is 1.8 m. Its centre of gravity is 1.05 m behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel.
Answer:
Question 13:
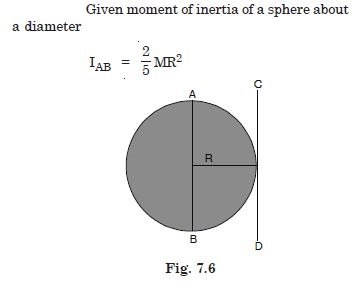
Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2MR2/5, where M is the mass of the sphere and R is the radius of the sphere.
Answer:
Question 14:
Give the moment of inertia of a disc of mass M and radius R about any of its diameters to be MR2/4, find its moment of inertia about an axis normal to the disc and passing through a point on its edge.
Answer:
Question 15:
Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time ?
Answer:
Question 16:
A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder ? What is the magnitude of angular momentum of the cylinder about its axis ?
Answer:
Kinetic energy associated with the rotation of the cylinder
Question 17:
A child stands at the centre of a turn-table with his two arms outstretched. The turn-table is set rotating with an angular speed of 40 rev/min. How much is angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to 2/5 times the initial value ? Assume that the turn-table rotates without friction.
Answer:
Question 18:
Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy ?
Answer:
Question 19:
A rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N ? What is the linear acceleration of the rope ? Assume that there is no slipping.
Answer:
Question 20:
To maintain a rotor at a uniform angular speed or 200 rad s–1, an engine needs to transmit a torque of 180 N m. What is the power required by the engine ? (Note : uniform angular velocity in the absence of friction implies zero torque. In practice, applied torque is needed to counter frictional torque). Assume that the engine is 100% efficient.
Answer:
Power = Torque × angular velocity
= 180 × 200
= 36000 W
= 36 kW.
Question 21:
From a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of gravity of the resulting flat body.
Answer:
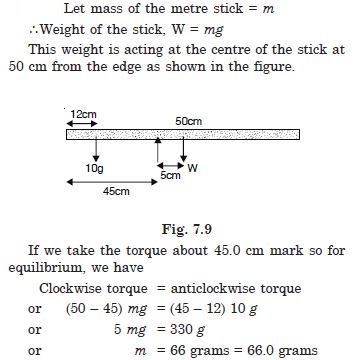
Question 22:
A metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5 g are put one on top of the other at the 12.0 cm mark, the stick is found to be balanced at 45.0 cm. What is the mass of the metre stick ?
Answer:
Question 23:
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination. Will it reach the bottom with the same speed in each case ?
Answer:
Yes, the velocity of both the solid spheres will be the same at the bottom of the inclined plane provided there is no friction.
Question 24:
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination. Will it take longer to roll down one plane than the other ?
Answer:
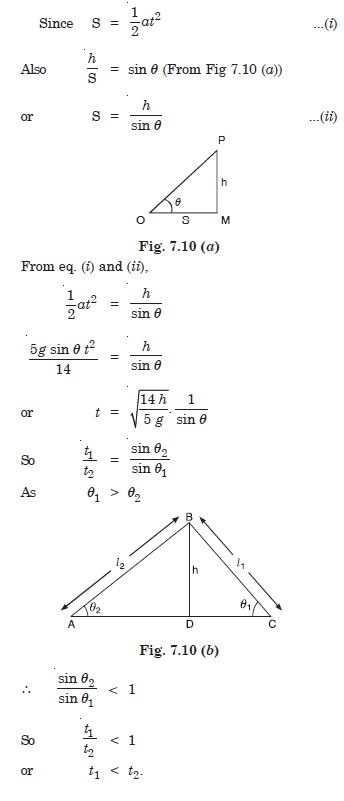
The time taken by the solid sphere will be longer when it roll down a plane with lesser inclination, because, the acceleration a is given by
Question 25:
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination. If so, which one and why ?
Answer:
Question 26:
A hoop of radius 2 m weighs 100 kg. It rolls along a horizontal floor so that its centre of mass has a speed of 20 cm s–1. How much work has to be done to stop it ?
Answer:
Question 27:
The oxygen molecule has a mass of 5.30 × 10–26 kg and a moment of inertia of 1.94 × 10–46 kg m2 about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is 500 ms–1 and that its kinetic energy of rotation is two-thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.
Answer:
Question 28:
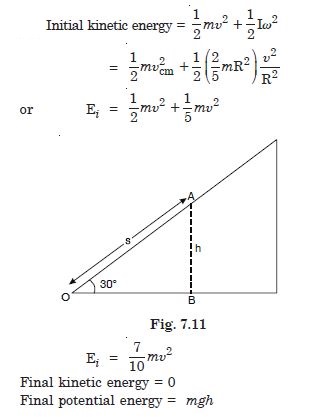
A cylinder rolls up an inclined plane of angle of inclination 30. At the bottom of the inclined plane the centre of mass of the cylinder has a speed
of 5 ms–1.
How far will the cylinder go up the plane ?
Answer:
Question 29:
A cylinder rolls up an inclined plane of angle of inclination 30. At the bottom of the inclined plane the centre of mass of the cylinder has a speed
of 5 ms–1.
How long will it take to return to the bottom ?