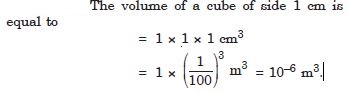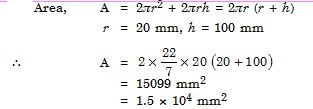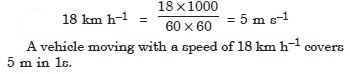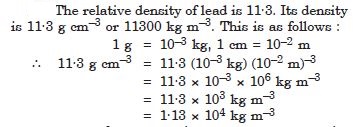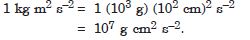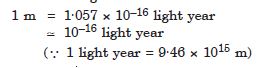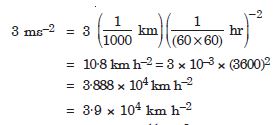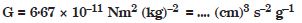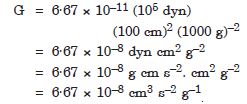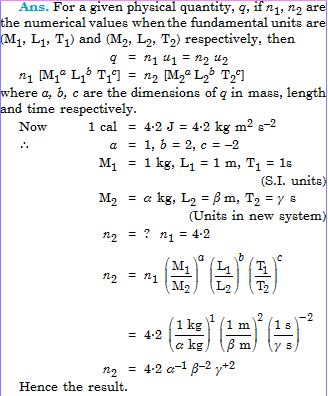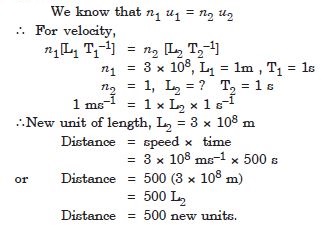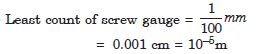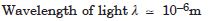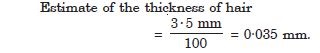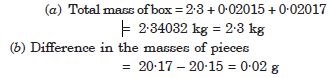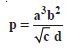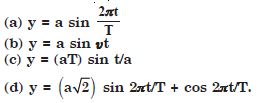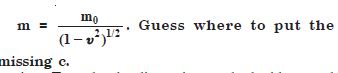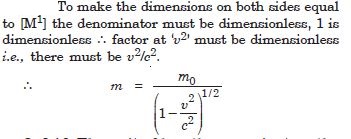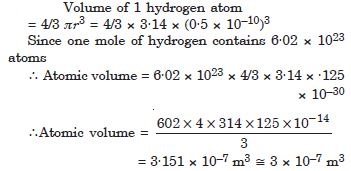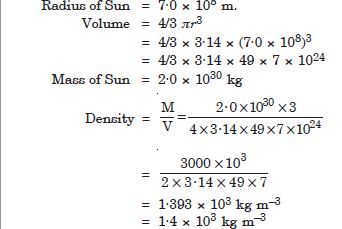NCERT Solutions for Class 11 Physics Chapter 2 - Units and Measurements

Question 1:

The volume of a cube of side 1 cm is equal to ........ M².

Question 2:

The surface area of a solid cylinder of radius 2 cm and height 10 cm is equal to ........... (mm)².

Question 3:

A vehicle moving with a speed of 18 km/h covers ......... m in 1s.

Question 4:

The relative density of lead is 11·3. Its density is ......... g cm^–2 or ............. kg m^–3.

Question 5:

Fill in the blanks by suitable conversion of units : 1 kg m² s^-2 = .......... g cm² s^-2/sup>

Question 6:

Fill in the blanks by suitable conversion of units : 1 m = .......... light year

Question 7:

Fill in the blanks by suitable conversion of units : 3 ms^–2 = .......... kmh^–2

Question 8:

Fill in the blanks by suitable conversion of units :

Question 9:

Question 10:

Question 11:

Question 12:

Which of the following is the most precise device for measuring length ?
A vernier callipers with 20 divisions on the sliding scale.

Question 13:

Which of the following is the most precise device for measuring length ?
A screw gauge of pitch 1 mm and 100 divisions on the circular scale.

Question 14:

Which of the following is the most precise device for measuring length ?
An optical instrument that can measure length to within a wavelength of light ?

Question 15:

A student measures the thickness of a human hair by looking at it through a microscope of magnification 100. He makes 20 observations and finds that the average width of the hair in the field of view of the microscope is 3·5 mm. What is the estimate of the thickness of hair ?

Question 16:

Answer the following :
You are given a thread and a metre scale. How will you estimate the diameter of this thread ?

Question 17:

Answer the following :
A screw gauge has a pitch of 1·0 mm and 200 divisions on the circular scale. Do you think it is possible to increase the accuracy of the gauge arbitrarily by increasing the number of divisions on the circular scale ?

Question 18:

Answer the following :
The mean diameter of a thin brass rod is to be measured by a vernier callipers. Why is a set of 100 measurements of the diameter expected to yield a more reliable estimate than a set of 5 measurements only ?

Question 19:

The photograph of a house occupies an area of 1·75 cm² on a 35 mm slide. The slide is projected on to a screen, and the area of the house on the screen is 1·55 m². What is the linear magnification of the projector-screen arrangement?

Question 20:

State the number of significant figures in the following :
0·007 m²

Question 21:

State the number of significant figures in the following :
2·64 × 10²⁴ kg

Question 22:

State the number of significant figures in the following :
0·2370 g cm^–2

Question 23:

State the number of significant figures in the following :
6·320 J

Question 24:

State the number of significant figures in the following :
6·032 Nm^–2

Question 25:

State the number of significant figures in the following :
0.0006032

Question 26:

The length, breadth and thickness of a rectangular sheet of metal are 4·234 m, 1·005 m and 2·01 cm respectively. Give the area and volume of the sheet to correct significant figures.

Question 27:

The mass of a box measured by a grocer’s balance is 2·3 kg. Two gold pieces of masses 20·15 g and 20·17 g are added to the box.
What is (a) the total mass of the box, (b) the difference in the masses of the pieces to correct significant figures ?

Question 28:

physical quantity l is related to four observations a, b, c and d as follows :

The percentage errors of measurement in a, b, c and d are 1%, 3%, 4% and 2% respectively. What is the percentage error in the quantity p ? If the value of p calculated using the above relation turns out to be 3·763, to what value should you round off the result ?

Question 29:

A book with many printing errors contains four different formulae for the displacement y of a particle undergoing a certain periodic motion :

[a = maximum distance of the particle, u = speed of particle. T = Time period of motion]. Rule out the wrong formulae on dimensional grounds.

Question 30:

A famous relation in physics relates ‘moving mass’ m to the ‘rest mass’ m₀ of a particle in terms of its speed u and the speed of light, c. (This relation first arose as a conse-quence of special relativity theory due to Albert Einstein). A boy recalls the relation almost correctly but forgets where to put the constant c. He writes :

Question 31:

Question 32:

One mole of an ideal gas at standard temperature and pressure occupies 22·4 litres (molar volume). What is the ratio of molar volume to the atomic volume of a mole of hydrogen ? (Take the size of hydrogen molecule to be about 1Å). Why is the ratio so large ?

Question 33:

Explain this common observation clearly. If you look out of the window of a fast-moving train, the nearby trees, houses etc. seem to move rapidly in a direction opposite to the train’s motion, but the distant objects (hill tops, the moon, the stars etc.) seem to be stationary.

Question 34:

The principle of ‘parallax’ is used in the determination of distance of nearby stars. The role of distant object O there is now taken by nearby distant stars. The baseline AB is the line joining the Earth’s two locations six months apart in its orbit around the Sun. That is, the baseline is about the diameter of the earth’s orbit = 3 × 10¹¹ m. However, even the nearest stars are so distant that with such a long baseline they show parallax only of the order 1 s of arc or so. A parsec is a convenient unit of length on the astronomical scale. It is the distance of an object that will show a parallax of 1s of arc from opposite ends of a baseline equal to the distance from the Earth to the Sun. How much is a parsec in terms of metre ?

Question 35:

The nearest star to our solar system is 4·29 light year away. How much is this distance in terms of parsec ? How much parallax would this star (named Alpha Centauri) show when viewed from two locations on the Earth six months apart in its orbit around the sun ?

Question 36:

Precise measurements of physical quantities are a need of modern times. For example, to ascertain the speed of an enemy fighter plane one must have an accurate method to find its positions at closely separated instants of time. Only then we can hope to shell it by an antiaircraft gun. This was the actual motivation behind the discovery of radar in World War II. Think of different examples in modern science where precision measurements of length, time, mass etc. are needed. Also, wherever you can, give a quantitative idea of the precision needed.

Question 37:

Just as precise measurements are necessary in science, it is equally important to be able to make rough estimates of quantities using rudimentary ideas and common observations.
Think of ways by which you can estimate the following : (where an estimate is difficult to obtain, try to get an upper bound on the quantity).
the total mass of rain-bearing clouds over India during the Monsoon

Question 38:

Just as precise measurements are necessary in science, it is equally important to be able to make rough estimates of quantities using rudimentary ideas and common observations. Think of ways by which you can estimate the following : (where an estimate is difficult to obtain, try to get an upper bound on the quantity). the mass of an elephant

Question 39:

Just as precise measurements are necessary in science, it is equally important to be able to make rough estimates of quantities using rudimentary ideas and common observations.
Think of ways by which you can estimate the following : (where an estimate is difficult to obtain, try to get an upper bound on the quantity).
the wind speed during a storm

Question 40:

Just as precise measurements are necessary in science, it is equally important to be able to make rough estimates of quantities using rudimentary ideas and common observations.
Think of ways by which you can estimate the following : (where an estimate is difficult to obtain, try to get an upper bound on the quantity).
the number of strands of hair on your head

Question 41:

Just as precise measurements are necessary in science, it is equally important to be able to make rough estimates of quantities using rudimentary ideas and common observations.
Think of ways by which you can estimate the following : (where an estimate is difficult to obtain, try to get an upper bound on the quantity).
the number of air molecules in your classroom.

Question 42:

The sun is a hot plasma (ionized matter) with its inner core at temperature exceeding 10⁷ K, and its outer surface at a temperature of about 6000 K. At these high temperatures no substance remains in a solid or liquid phase. In what range do you expect the mass density of the Sun to be ? In the range of densities of solids and liquids or gases ? Check if your guess is correct from the following data : mass of the Sun = 2·0 × 10³⁰ kg, radius of the Sun
= 7·0 × 10⁸ m.

Question 43:

When the planet Jupiter is at a distance of 824.7 million km from the earth, its angular diameter is measured to be 35.72 s of arc. Calculate the diameter of Jupiter.