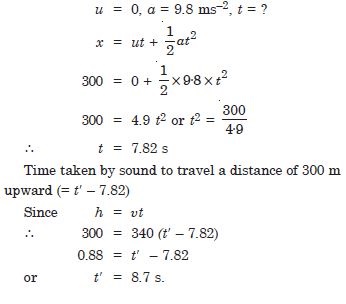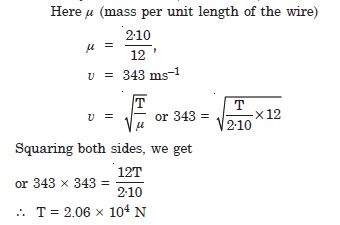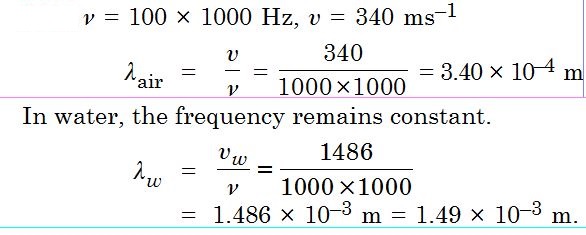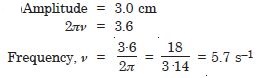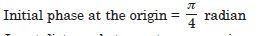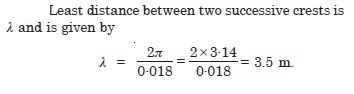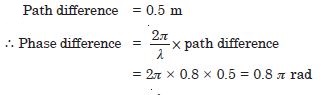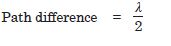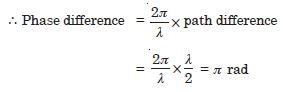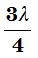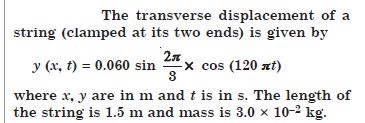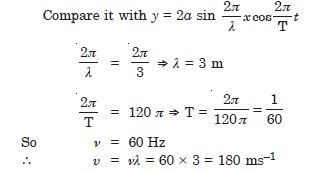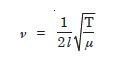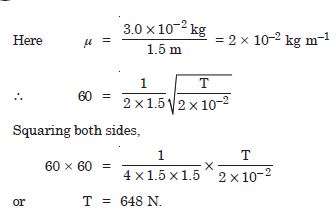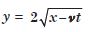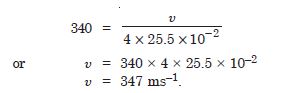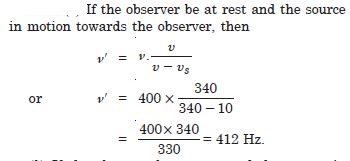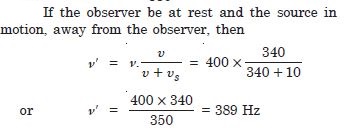NCERT Solutions for Class 11 Physics Chapter 15 - Waves

Question 1:

A string of mass 2.50 kg is under a tension of 200 N. The length of the stretched string is 20.0 m. If a transverse jerk is struck at one end of the string, how long does the disturbance take to reach the other end ?

Question 2:

A stone dropped from the top of a tower 300 m high splashes to the water of a pond near the base of the tower. When is the splash heard at the top given that the speed of sound in air is 340 ms^–1 ? (g = 9.8 ms^–2).

Question 3:

A steel wire has a length of 12.0 m and a mass of 2.10 kg. What should be the tension in the wire so that the speed of a transverse wave on the wire equals the speed of sound in dry air at 20$°$C ( = 343 ms^–1) ?

Question 4:

Question 5:

Question 6:

A bat emits ultrasonic sound of frequency 1000 kHz in air. If this sound meets a water surface, what is the wavelength of (a) the reflected sound, (b) the transmitted sound ? Speed of sound in air = 340 ms^–1, and in water = 1486 ms^–1.

Question 7:

A hospital uses an ultrasonic scanner to locate tumours in a tissue. What is the wavelength of sound in a tissue in which the speed of sound is 1.7 km s^–1 ? The operating frequency of the scanner is 4.2 MHz.

Question 8:

Is this a travelling wave or a stationary wave ? If it is travelling. What are the speed and direction of its propagation ?

Question 9:

What are its amplitude and frequency ?

Question 10:

What is the initial phase at the origin ?

Question 11:

What is the least distance between two successive crests in the wave ?

Question 12:

For the wave described in Question 15.8, plot the displacement (y) versus time (t) graphs for x = 0.2 and 4 cm. What are the shapes of these graphs ? In which aspects does the oscillatory motion in a travelling wave differ from one point to another : amplitude, frequency or phase ?

Question 13:

For the travelling harmonic wave
y (x, t) = 2.0 cos 2p (10t – 0.0080 x + 0.35),
where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of 4 m,

Question 14:

For the travelling harmonic wave
y (x, t) = 2.0 cos 2p (10t – 0.0080 x + 0.35),
where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of 0.5 m,

Question 15:

For the travelling harmonic wave
y (x, t) = 2.0 cos 2p (10t – 0.0080 x + 0.35),
where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of $\mathrm{\lambda }$/2

Question 16:

For the travelling harmonic wave
y (x, t) = 2.0 cos 2p (10t – 0.0080 x + 0.35),
where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of

Question 17:

Does the function represent a travelling or a stationary wave ?

Question 18:

Interpret the waves as a superposition of two waves travelling in opposite directions. What are the wavelength, frequency and speed of propagation of each wave ?

Question 19:

Determine the tension in the string.

Question 20:

Given below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent (i) a travelling wave, (ii) a stationary wave or (iii) none of all y = 2 cos (3x) sin (10t)

Question 21:

Given below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent (i) a travelling wave, (ii) a stationary wave or (iii) none of all

Question 22:

Given below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent (i) a travelling wave, (ii) a stationary wave or (iii) none of all
y = 3 sin (5x – 0.5 t) + 4 cos (5x – 0.5 t)

Question 23:

Given below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent (i) a travelling wave, (ii) a stationary wave or (iii) none of all
y = cos x sin t + cos 2x sin 2t.

Question 24:

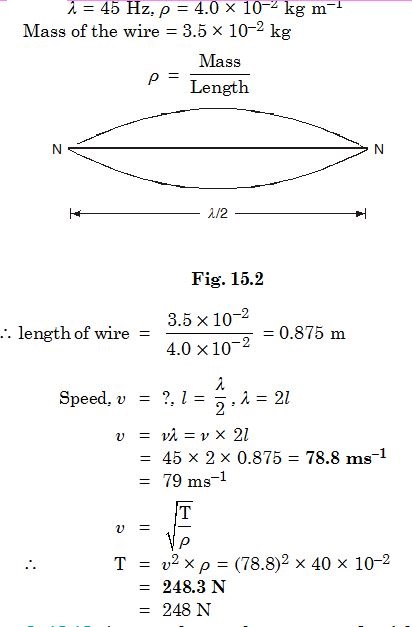
A wire stretched between two rigid supports vibrates in its fundamental node with a frequency of 45 Hz. The mass of the wire is 3.5 × 10^–2 kg and its linear mass density is 4.0 × 10^–2 kg m^–1. What is (a) the speed of a transverse wave on the string, and (b) the tension in the string ?

Question 25:

A metre long tube at one end, with a movable piston at the other end, shows resonance with a fixed frequency source (a tuning fork of frequency 340 Hz) when the tube length is 25.5 cm or 79.3 cm. Estimate the speed of sound in air at the temperature of the experiment. The edge effects may be neglected.

Question 26:

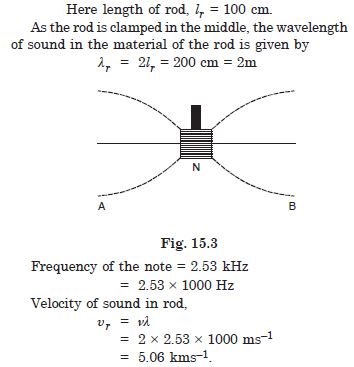
A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod is given to be 2.53 kHz. What is the speed of sound in steel ?

Question 27:

A pipe 20 cm long is closed at one end. Which harmonic mode of the pipe is resonantly excited by a 430 Hz source ? Will this same source be in resonance with the pipe of its both ends are open ? (Speed of sound in air is 340 ms^–1)

Question 28:

Two sitar strings A and B playing the note ‘Ga’ are slightly out of tune and produce beats of frequency 6 Hz. The tension in the string A is slightly reduced and the beat frequency is found to reduce to 3 Hz. If the original frequency of A is 324 Hz, what is the frequency of B ?

Question 29:

Explain why (or how)
In a sound wave, a displacement node is a pressure antinode and vice versa.

Question 30:

Explain why (or how)
bats can ascertain distances, directions, nature and size of the obstacles without any “eye”.

Question 31:

Explain why (or how)
a violin note and a sitar note may have the same frequency, yet we can distinguish between the two notes.

Question 32:

Explain why (or how)
solids can support both longitudinal and transverse waves, but only longitudinal waves can propagate in gases.

Question 33:

Explain why (or how)
the shape of a pulse gets distorted during propagation in a dispersive medium.

Question 34:

A train standing at the outer signal of a railway station blows a whistle of frequency 400 Hz in still air. (i) What is the frequency of the whistle for a platform observer when the train approaches the platform with a speed of 10 ms^–1,

Question 35:

A train standing at the outer signal of a railway station blows a whistle of frequency 400 Hz in still air. (i) What is the frequency of the whistle for a platform observer when the train recedes from the platform with a speed of 10 ms^–1 ?

Question 36:

A train standing at the outer signal of a railway station blows a whistle of frequency 400 Hz in still air. (i) What is the frequency of the whistle for a platform observer when the train What is the speed of sound in each case ? The speed of sound in still air can be taken as 340 ms^–1.

Question 37:

A train standing at a station-yard blows a whistle of frequency 400 Hz in still air. A wind starts blowing in the direction from the yard to the station with a speed of 10 ms–1. What are the frequency, wavelength and speed of source for an observer standing on the station’s platform ? Is the situation exactly identical to the case when the air is still and the observer runs towards the yard at a speed of 10 ms–1 ? The speed of sound in still air can be taken as 340 ms^–1.