Question 1:
A map projection least suitable for the world map:
- Mercator
- Simple Cylindrical
- Conical
- All the above
Answer:
(c). Conical
Question 2:
A map projection that is neither the equal area nor the correct shape and even the directions are also incorrect.
- Simple Conical
- Polar zenithal
- Mercator
- Cylindrical
Answer:
(d). Cylindrical
Question 3:
A map projection having correct direction and correct shape but area greatly exaggerated polewards is
- Cylindrical Equal Area
- Mercator
- Conical
- All the above
Answer:
(b). Mercator
Question 4:
When the source of light is placed at the centre of the globe, the resultant projection is called.
- Orthographic
- Stereographic
- Gnomonic
- All the above
Answer:
(c). Gnomonic
Question 5:
Describe the elements of map projection.
Answer:
The elements of map projection are as
following:
1. Reduced earth: The earth’s model is
represented with the help of a reduced scale on
a flat sheet of paper on this model the network
of graticule can be translated.
2. Parallels of latitude: These are the circles
round the globe parallel to the equator and
maintaining uniform distance from the poles.
They are demarcated as 0° to 90° North and
South.
3. Meridians of longitudes: Longitues are the
elements of map projections. There are also
drawn north to south direction from one pole
to another and two opposite meridians make a
complete circle.
4. Global property: Distance between any given
points of a region shape of the region, size or
area of the region in accuracy are given in it.
Question 6:
What do you mean by global property?
Answer:
The global property means the
1. Correctners of the area
2. Direction
3. Distance
4. and shape of the area.
Question 7:
Not a single map projection represents the globe truly. Why?
Answer:
Map projection project the network of latitudes and longitudes on a plain surface by using the geometrical and mathematical methods. The globe is the true representation of earth. The projections given a shadowed picture of the globe which is distorted in those parts which are further away from the point where the paper touches the globe.
Question 8:
How is the area kept equal in cylindrical equal area projection?
Answer:
The area is kept equal in cylindrical equal area projection because the parallels and meridians are projected as straight lines intersecting one another at right angles.
Question 9:
Differentiate between: Developed and non-developed surface.
Answer:
Developed Surface: A developed surface is
a surface which can be unrolled into a plane surface.
For e.g. a plane, a cylinder and a cone are developable
surfaces.
Undeveloped surface: An undeveloped surface
can not unroll into a place just as a globe.
Question 10:
Differentiate between: Homolographic and Orthographic projections.
Answer:
Homolographic projection: These are the projections which are graticule of latitudes and longitudes on the map its equal in area. Orthographic Projection: On these projections the correct shape of the area of a country is shown.
Question 11:
Differentiate between: Normal and Oblique projections.
Answer:
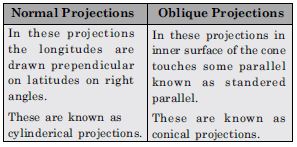
Question 12:
Differentiate between: Parallels of latitudes and meridians of longitues.
Answer:

Question 13:
Discuss the criteria used for classifying map projection and state the major characteristics of each type of projection.
Answer:
Map Projections: Globe is the best and
accurate model of the earth. There are many problems
in representing the spherical globe on a flat sheet of
paper. Map projections are the means of transferring
the lines of latitude and lines of longitude of the globe
on to a flat sheet of paper. The expansion of a
photograph on a screen in a cinema hall is an example
of Projection. By this method, the lines of latitude and
lines of longitude are projected on a flat sheet of paper.
Classification of map projections: Different
types of map projections are used. These are classified
on the following bases:
1. On the basis of source of light: On this basis,
the projections are of two types:
(a) Perspective projections
(b) Non-Perspective projections.
Perspective projections are prepared on the basis
of Geometry. In these projections, shadow of
lines of latitude and longitude are drawn on the
basis of the location of source of light. Source of
light can be placed at different positions.
Non-perspective projections are called
mathematical projections. In these projections,
source of light is not used. Principles of
mathematics are used to draw these projections.
2. On the basis of purpose:
(a) Equal-area Projection: With the help of these
projections, the equal-area property of a map is
preserved. These are called Homolographic
projections also. These are used for preparing
distribution maps.
(b) Orthomorphic Projections: On these
projections, the correct shape of an area or a
country is shown.
(c) Azimuthal Projections: These map
projections help to preserve the property of
correct direction on a map. These are used for
preparing maps for sailors and for air-navigators.
3. On the basis of construction:
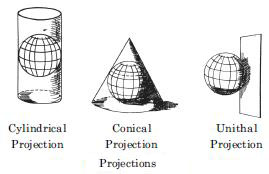
(a) Cylindrical Projections: In these projections,
it is imagined that a hollow cylinder
circumscribes the globe. The equator of the globe
touches the cylinder so that the length of the
equator remains correct. In this group, the
following non-perspective projections are
included:
(i) Simple cylindrical projection
(ii) Cylindrical equal area projection
(iii) Mercator’s projection.
In these projections, lines of latitude are parallel
to the equator and are straight lines. The
meridians are vertical straight-lines. These lines
intersect each other at right angles.
(b) Conical Projections: In this projection, the
cone is used as a surface. It is imagined that
the cone is placed on the globe so that its vertex
is above the pole. The axis of the cone coincides
with that of the globe. The parallel along which
the cone touches the globe is called the standard
parallel. It keeps correct length. The parallels
are shown by concentric arcs of circles.
Meridians are straight lines drawn at equal
angular distance.
In this group, the following map projections are
included:
(i) Simple Conical Projection with one
standard parallel.
(ii) Conical Projection with two standard
parallels
(iii) Bonne’s Projection
(iv) Polyconic Projection.
(c) Zenithal Projections: In these projections, it
is assumed that a plane surface is placed
tangentially at the pole of the globe. These are
azimuthal projections showing correct bearing.
These are used for polar areas. According to the
position of the source of light, these projections
are perspective projections.
(i) Polar Zenithal Gnomonic Projection.
(ii) Polar Zenithal stereographic Projection.
(iii) Polar Zenithal orthographic Projection.
In this group, two non-perspective zenithal
projections of zenithal equidistant projection and
zenithal equal area projection are also included.
(d) Conventional Projection: These projections
are mathematical projections. These are called
conventional projections, because no surface is
used in these. These are drawn for specific
purpose of drawing world maps. These include
the Sinusoidal projection and Mollweide’s
projections.
Importance of Map Projections
(i) Map projections are useful for drawing maps on
a flat sheet of paper.
(ii) These provide knowledge about the true shape of
the earth.
(iii) Atlas maps and wall maps are prepared on the
basis of map projections.
(iv) Different types of maps are prepared with the
help of map projections.
(v) These help us to know the location of lines of
latitude and lines of longitude.
(vi) Map projections are used to draw distribution
maps, political maps, and maps of ocean routes,
air routes and ocean currents.
Question 14:
Which map projection is very useful for navigational pruposers? Explain the main properties and limitations of this projection?
Answer:
The Mercater projection is an orthomorphic
projection and very useful for the navigational
purposes. The properties and limitations are as
under:
Properties of Mercator’s Projection
(1) It is a cylindrical projection which was developed
by a Dutch Cartographer Mercator in 1569.
(2) It is a non-perspective projection.
(3) The parallels are straight lines parallel and equal
to Equator.
(4) Meridians are perpendiculars drawn at equal
distances.
(5) Meridians and parallels intersect at right-angles.
(6) Scale along equator is correct. But it increases
along other parallels as we move towards poles.
Pole is a point but it is drawn equal to equator.
So, it is exaggerated infinite.
(7) Scale along meridians is also exaggerated.
Limitations:
(1) Poles can not be shown on this projection.
(2) The scale in polar area is exaggerated many times.
So the area is increased in polar areas.
Question 15:
Discuss the main properties of conical projection with one standard parallel and discribe its major limitations.
Answer:
Properties:
(i) The Pole and all the lines of
latitude are concentric arcs of circles.
(ii) Meridians are straight lines radiating from
the vertex.
(iii) Parallels intersect Meridians at right angles.
Merits: Scale along the standard parallel is
correct. Projection is satisfactory for areas in
the neighbourhood of standard parallel.
Demerits: This projection is neither equal in
area nor in orthomorphic. It is not azimuthal.
Uses: This projection is useful for small areas
with small north-south extent, but not for a
large east-west extent such as Trans-Siberian
Railway.
