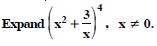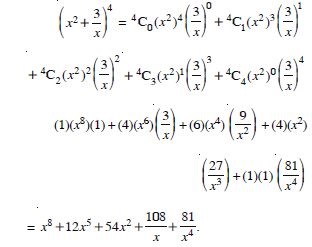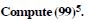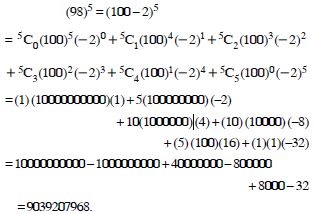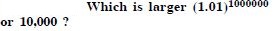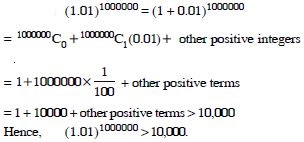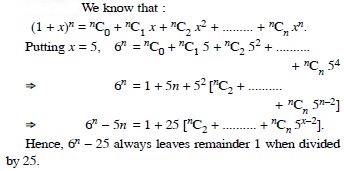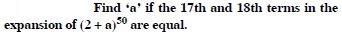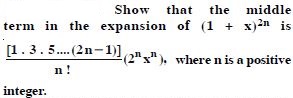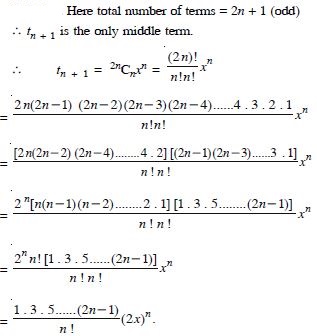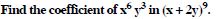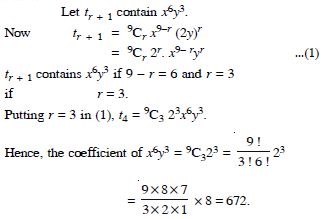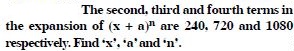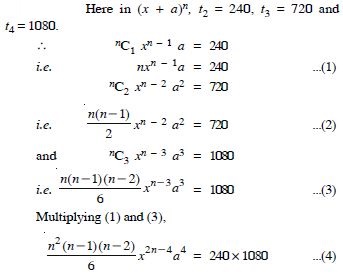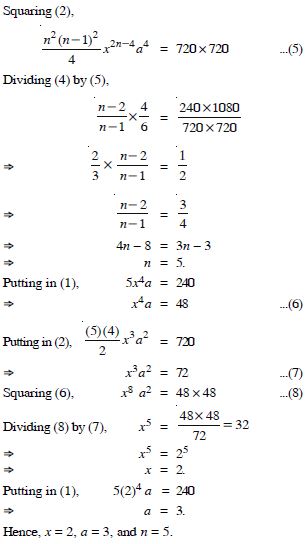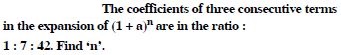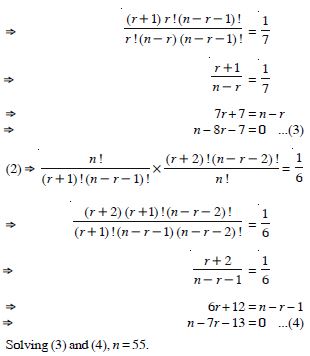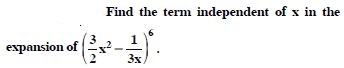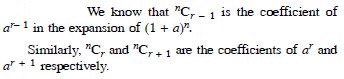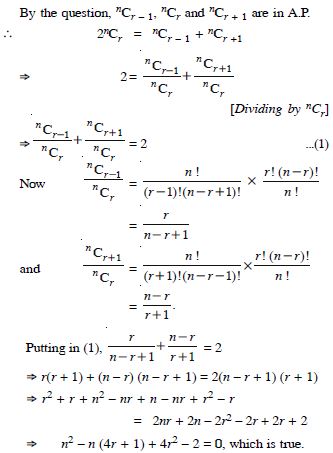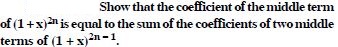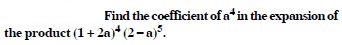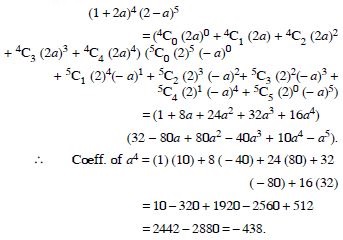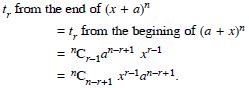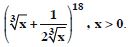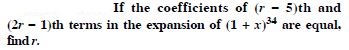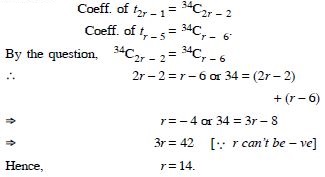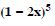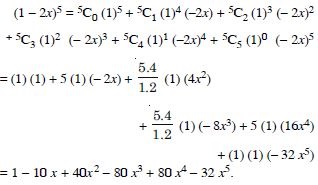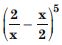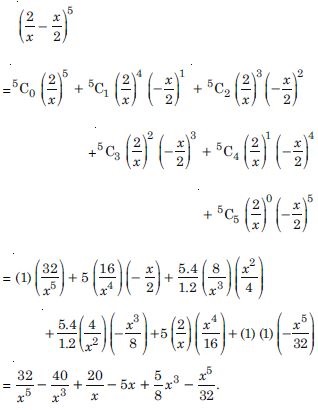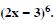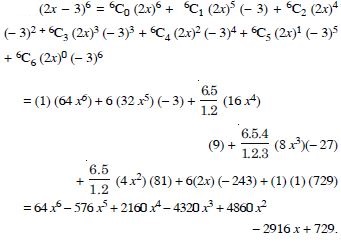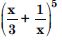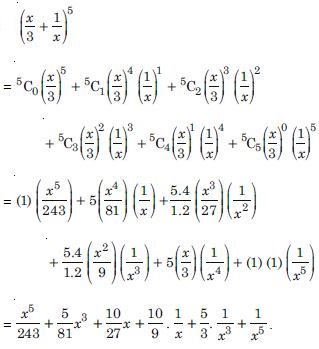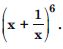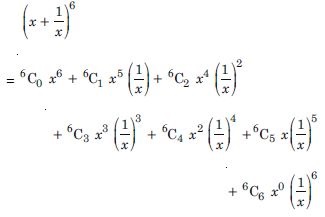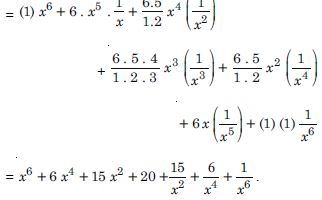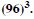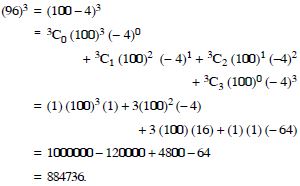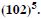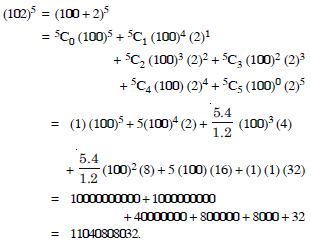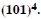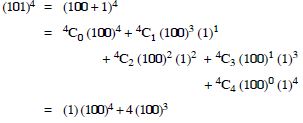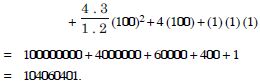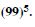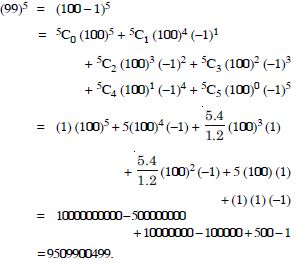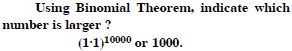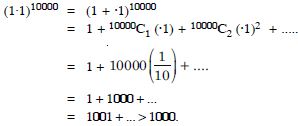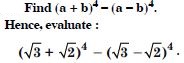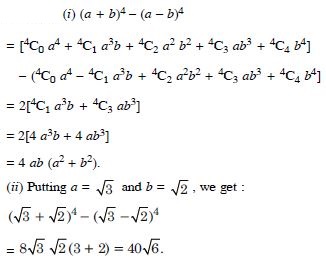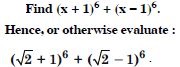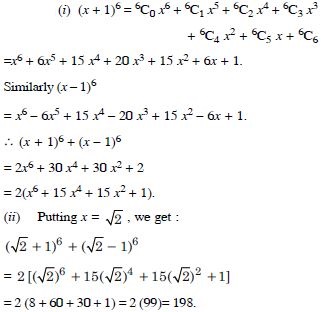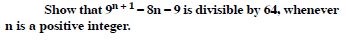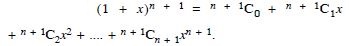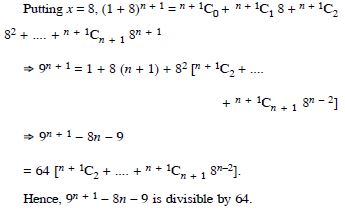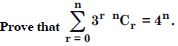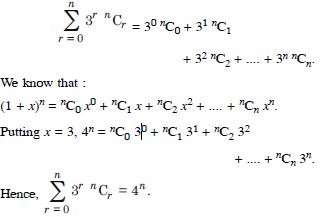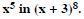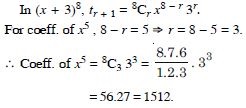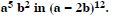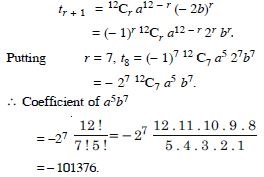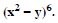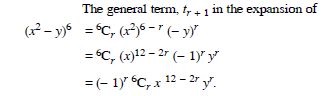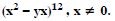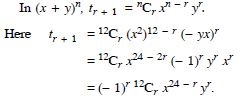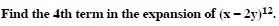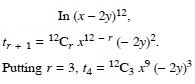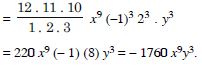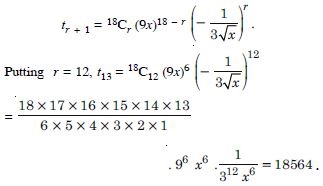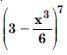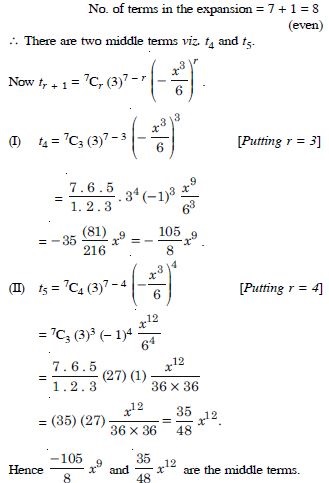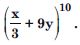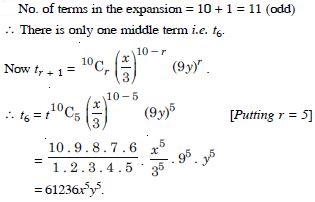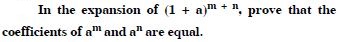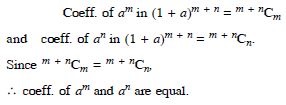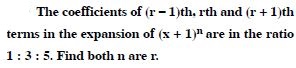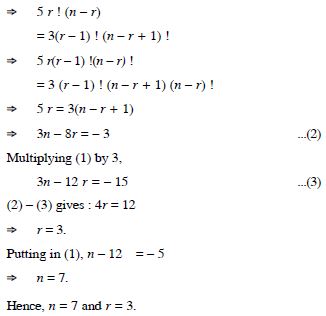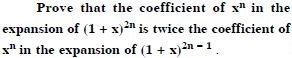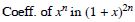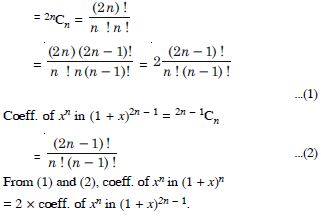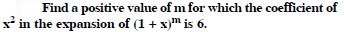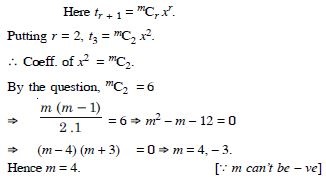Class 11 students can access free NCERT Solutions at Aasoka anytime anywhere. These solutions include questions and solutions designed by subject matter experts as per the latest CBSE syllabus. Students can start their preparation with NCERT Solutions for Class 11 and boost their overall performance. The solutions are written in an easy-to-understand language so students can easily study from these and score excellent marks in their exams.
In the “Binomial Theorem” chapter of Maths Class 11 students will learn Pascal’s triangle, the binomial theorem for positive integral indices, general and middle terms in binomial expansion, and much more.
Question 1:
Answer:
Question 2:
Answer:
Question 3:
Answer:
Question 4:
Answer:
Question 5:
Answer:
Question 6:
Answer:
Question 7:
Answer:
Question 8:
Answer:
Question 9:
Answer:
Question 10:
Answer:
Question 11:
Answer:
Question 12:
Answer:
Question 13:
Answer:
Question 14:
Find the rth term from the end of (x + a)n.
Answer:
Question 15:
Find the term independent of x in the expansion of :
Answer:
Question 16:
Answer:
Question 17:
Answer:
Question 18:
Expand each of the expressions in:
Answer:
Question 19:
Expand each of the expressions in:
Answer:
Question 20:
Expand each of the expressions in:
Answer:
Question 21:
Expand each of the expressions in:
Answer:
Question 22:
Expand each of the expressions in:
Answer:
Question 23:
Using binomial Theorem, evaluate each of the following :
Answer:
Question 24:
Using binomial Theorem, evaluate each of the following :
Answer:
Question 25:
Using binomial Theorem, evaluate each of the following :
Answer:
Question 26:
Using binomial Theorem, evaluate each of the following :
Answer:
Question 27:
Answer:
Question 28:
Answer:
Question 29:
Answer:
Question 30:
Answer:
Question 31:
Answer:
Question 32:
Find the coefficient of :
Answer:
Question 33:
Find the coefficient of :
Answer:
Question 34:
Write the general term in the expansion of :
Answer:
Question 35:
Write the general term in the expansion of :
Answer:
Question 36:
Answer:
Question 37:
Answer:
Question 38:
Find the middle terms in the expansion of :
Answer:
Question 39:
Find the middle terms in the expansion of :
Answer:
Question 40:
Answer:
Question 41:
Answer:
Question 42:
Answer:
Question 43:
Answer:
