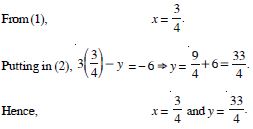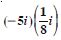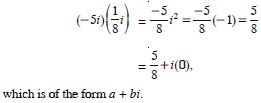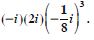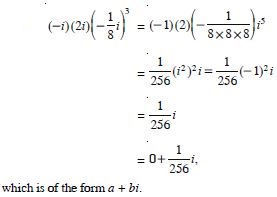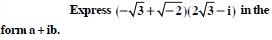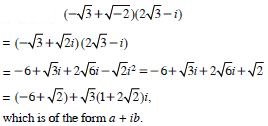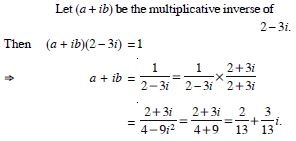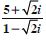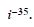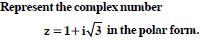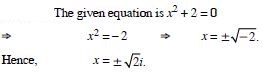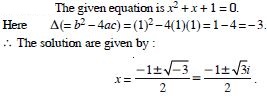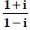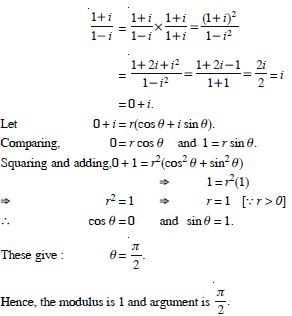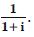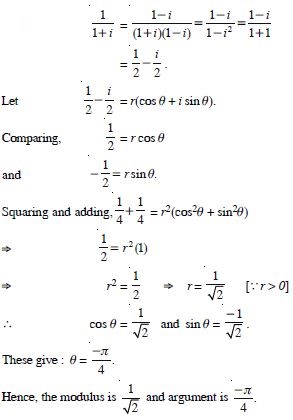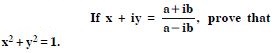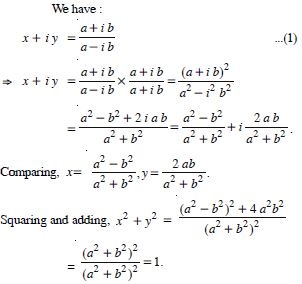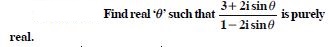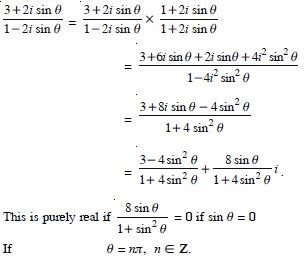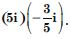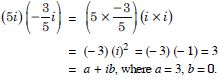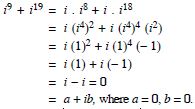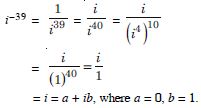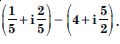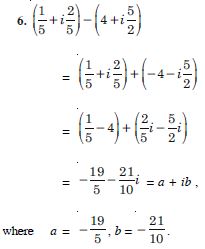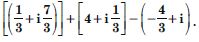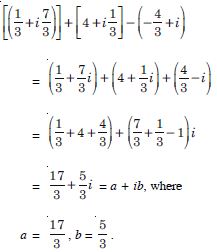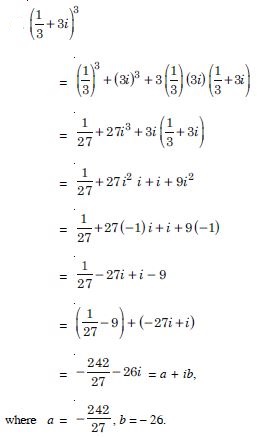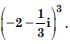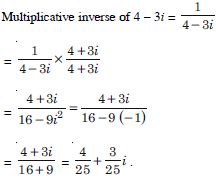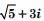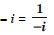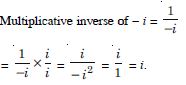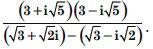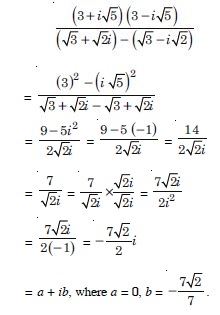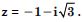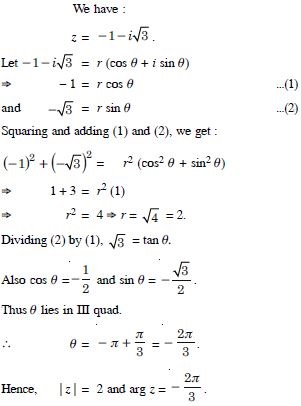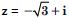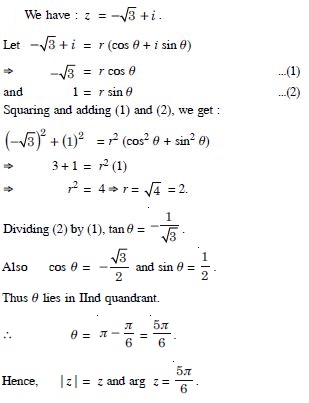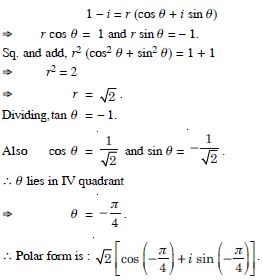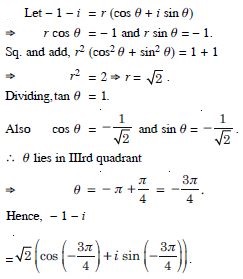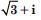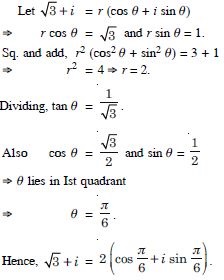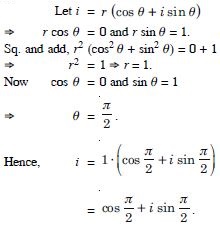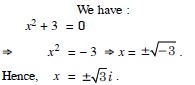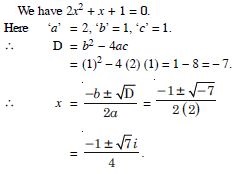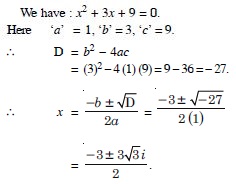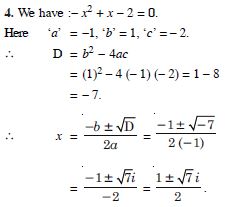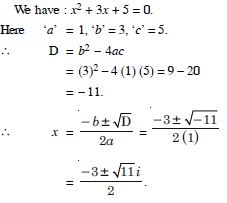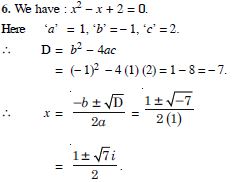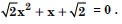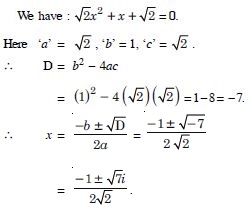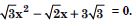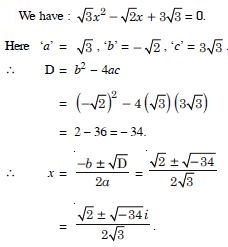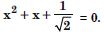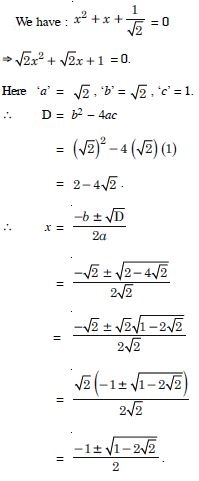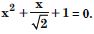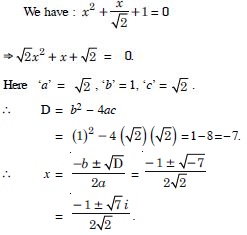The subject matter experts have designed NCERT Solutions at Aasoka for free of cost. These solutions can be easily accessed by students anytime anywhere. The NCERT Solutions for Class 11 allow students to study at their own pace and master each concept thoroughly. The experts have followed the latest CBSE syllabus and guidelines and accordingly framed questions and answers. For effective exam preparations, these solutions are the key. Study from NCERT Solutions and score the marks you desire.
Topics covered under Class 11 Maths chapter “Complex Numbers” are Argand plane, De-Moivre’s theorem, formation of polynomial equation, the definition of complex numbers, loci in the complex plane, need for complex numbers, quadratic expression, the transformation of equations, algebra of complex numbers, polar representation of complex numbers, polar form, theory of equations, the conjugate of a complex number, max and min value of the quadratic expression, statement of the fundamental theorem of algebra, nature of roots and graphs, algebraic properties of complex numbers, square root and cube root of the complex number, max and min value of the rational expression, modulus, resolution into two linear factors, etc.
Question 1:
If 4x + i(3x – y) = 3 + i(–6), where x and y are real numbers, then find the values of x and y.
Answer:
We have : 4x + i(3x – y) = 3 + i(–6).
Comparing real and imaginary parts, we get :
4x = 3 ...(1)
and 3x – y = – 6 ...(2)
Question 2:
Express the following in the form of a + bi :
Answer:
Question 3:
Express the following in the form of a + bi :
Answer:
Question 4:
Express (5 – 3i)3 in the form a + ib.
Answer:
(5 – 3i)3= 53 – 3 × 52 × (3i) + 3 × 5 × (3i)2
–
(3i)3
= 125 – 225i + 135(i)2 – 27i3
= 125 – 225i – 135 + 27i
= –10 – 198i,
which is of the form a + ib.
Question 5:
Answer:
Question 6:
Find the multiplicative inverse of 2 – 3i.
Answer:
Question 7:
Express the following in the form a + ib :
Answer:
Question 8:
Express the following in the form a + ib :
Answer:
Question 9:
Answer:
Question 10:
Answer:
Question 11:
Solve : x2 + 2 = 0.
Answer:
Question 12:
Solve : x2 + x + 1 = 0.
Answer:
Question 13:
Answer:
Question 14:
Answer:
Question 15:
Find the modulus and argument of the complex numbers :
Answer:
Question 16:
Find the modulus and argument of the complex numbers :
Answer:
Question 17:
Answer:
Question 18:
Answer:
Question 19:
Answer:
Question 20:
Express each of the complex numbers given in the form a + ib.
Answer:
Question 21:
Express each of the complex numbers given in the form a + ib.
i9 + i19.
Answer:
Question 22:
Express each of the complex numbers given in the form a + ib.
i–39
Answer:
Question 23:
Express each of the complex numbers given in the form a + ib.
3 (7 + i7) + i (7 + i7).
Answer:
3 (7 + i7) + i (7 + i7)
= (21 + 21i) + (7i + 7i2)
= (21 + 21i) + (7i – 7)
= (21 – 7) + (21i + 7i)
= 14 + 28i
= a + ib, where a = 14, b = 28.
Question 24:
Express each of the complex numbers given in the form a + ib.
(1 – i) – (– 1 + i6).
Answer:
(1 – i) – (– 1 + i6) = (1 – i) + (1 – 6i)
= (1 + 1) + (– i – 6i) = 2 – 7i
= a + ib, where a = 2, b = – 7.
Question 25:
Express each of the complex numbers given in the form a + ib.
Answer:
Question 26:
Express each of the complex numbers given in the form a + ib.
Answer:
Question 27:
Express each of the complex numbers given in the form a + ib.
(1 – i)4.
Answer:
Question 28:
Express each of the complex numbers given in the form a + ib.
Answer:
Question 29:
Express each of the complex numbers given in the form a + ib.
Answer:
Question 30:
Find the multiplicative inverse of each of the complex
numbers given in
4 – 3i
Answer:
Question 31:
Find the multiplicative inverse of each of the complex numbers given in
Answer:
Question 32:
Find the multiplicative inverse of each of the complex numbers given in
Answer:
Question 33:
Express the following expression in the form a + ib :
Answer:
Question 34:
Find the modulus and the argument of each of the complex number in
Answer:
Question 35:
Find the modulus and the argument of each of the complex number in
Answer:
Question 36:
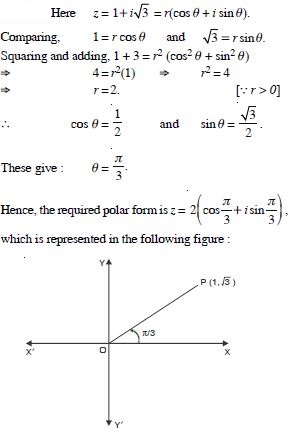
Convert each of the complex numbers given in the polar form :
1 – i
Answer:
Question 37:
Convert each of the complex numbers given in the polar form :
– 1 + i
Answer:
Question 38:
Convert each of the complex numbers given in the polar form :
– 1 – i
Answer:
Question 39:
Convert each of the complex numbers given in the polar form :
– 3
Answer:
Let – 3 = r (cos + i sin )
r cos = – 3 and r sin = 0.
Sq. and add, r2 (cos2 + sin2 ) = 9 + 0
r2 = 9 r = 3.
Dividing, tan = 0.
Also cos = – 1, and sin = 0.
Thus = .
Hence, – 3 = 3 (cos + i sin ).
Question 40:
Convert each of the complex numbers given in the polar form :
Answer:
Question 41:
Convert each of the complex numbers given in the polar form : i
Answer:
Question 42:
Solve each of the following equations :
x2 + 3 = 0.
Answer:
Question 43:
Solve each of the following equations :
2x2 + x + 1 = 0.
Answer:
Question 44:
Solve each of the following equations :
x2 + 3x + 9 = 0.
Answer:
Question 45:
Solve each of the following equations :
– x2 + x – 2 = 0.
Answer:
Question 46:
Solve each of the following equations :
x2 + 3x + 5 = 0.
Answer:
Question 47:
Solve each of the following equations :
x2 – x + 2 = 0.
Answer:
Question 48:
Solve each of the following equations :
Answer:
Question 49:
Solve each of the following equations :
Answer:
Question 50:
Solve each of the following equations :
Answer:
Question 51:
Solve each of the following equations :