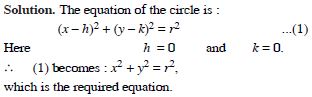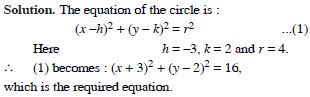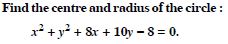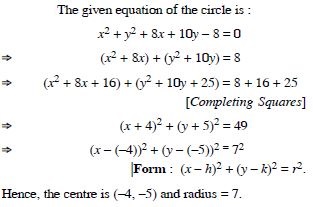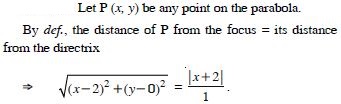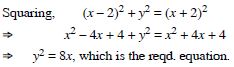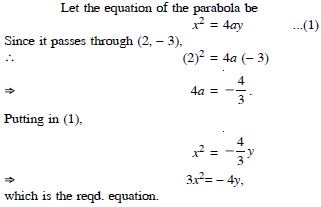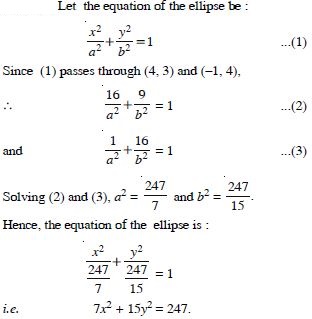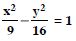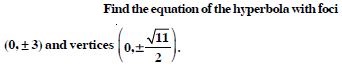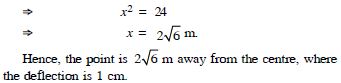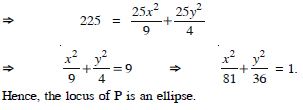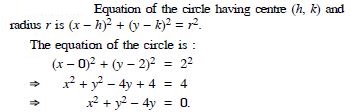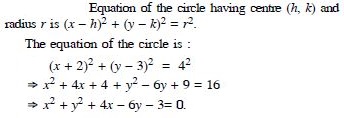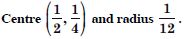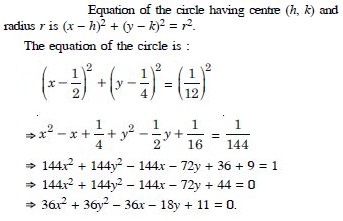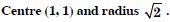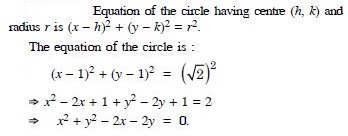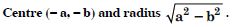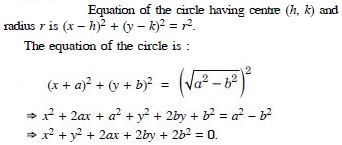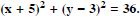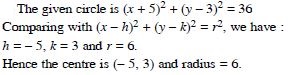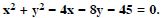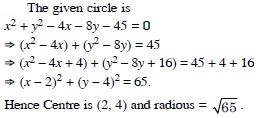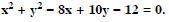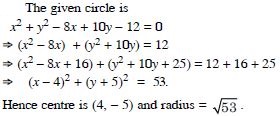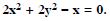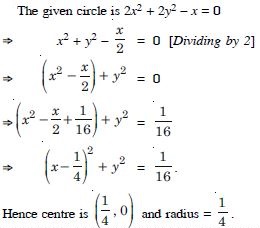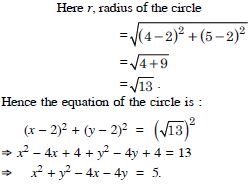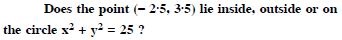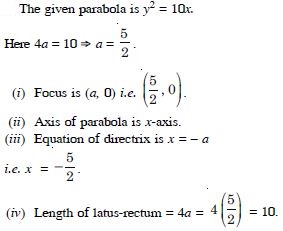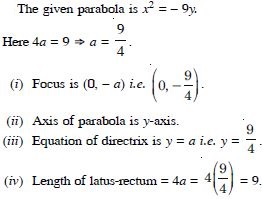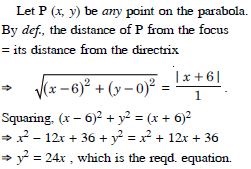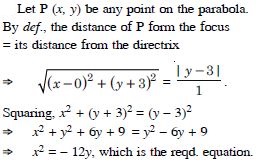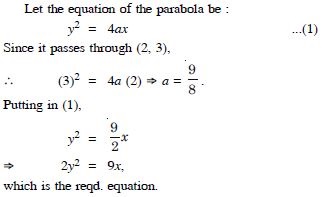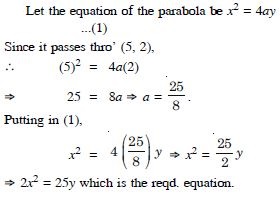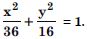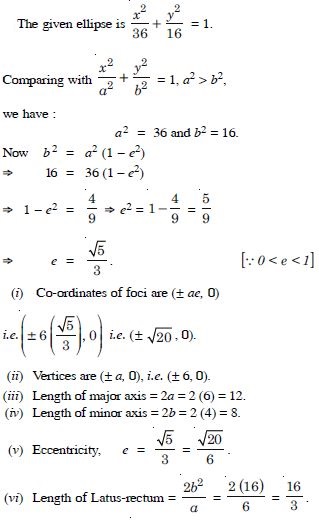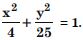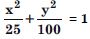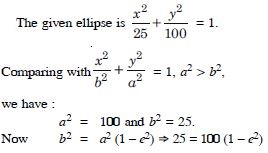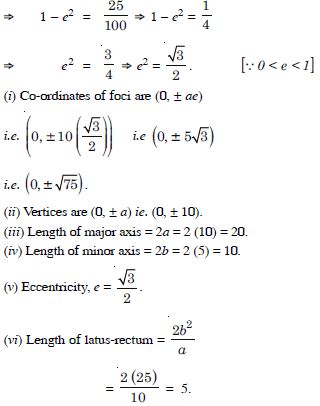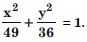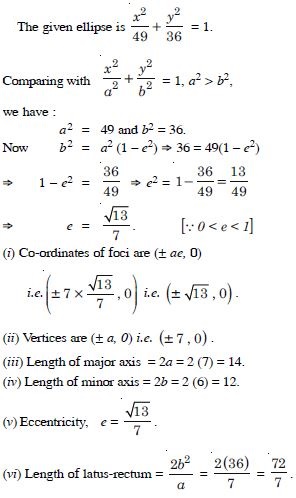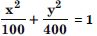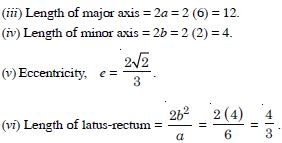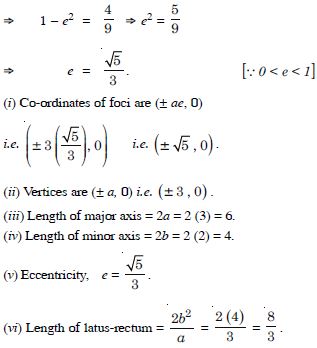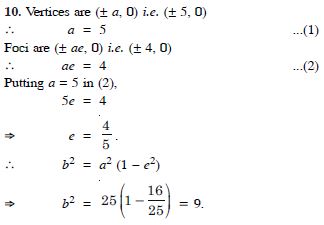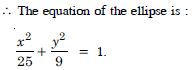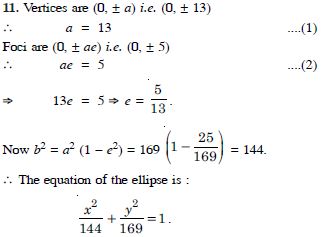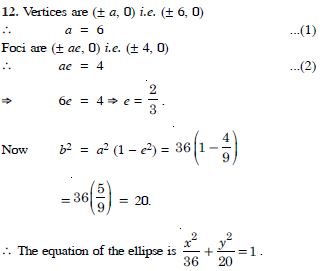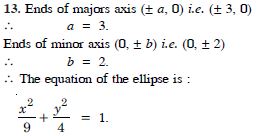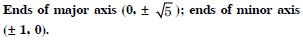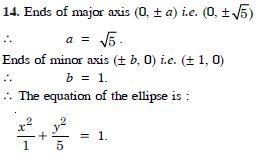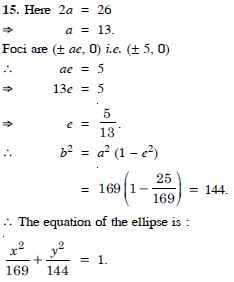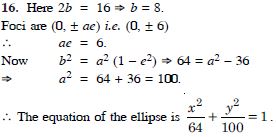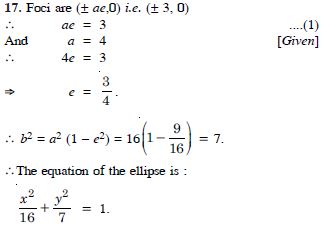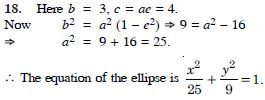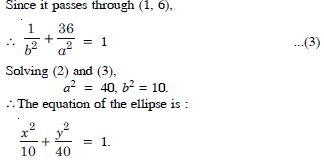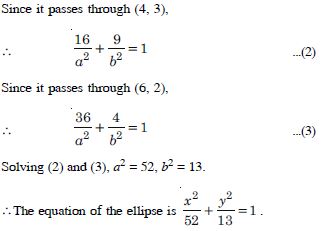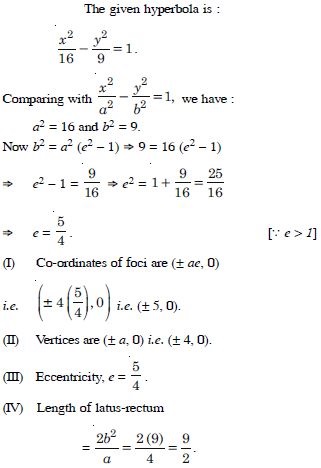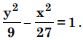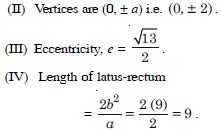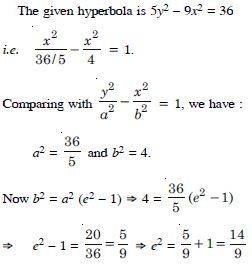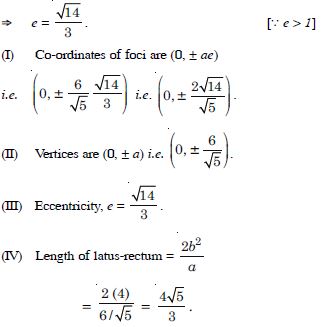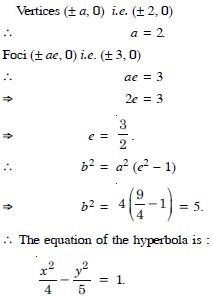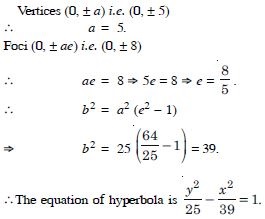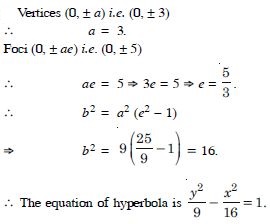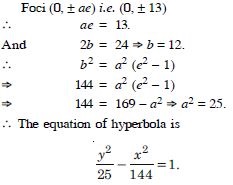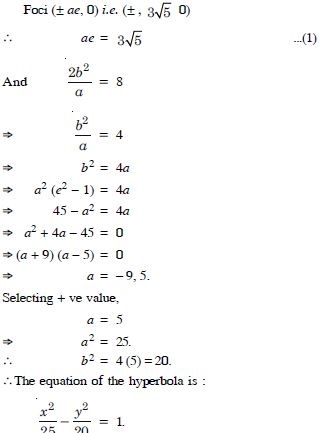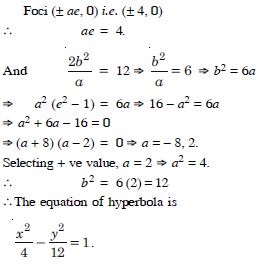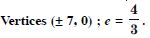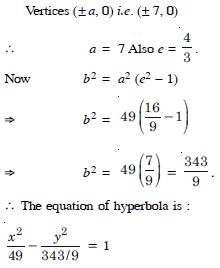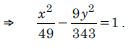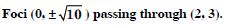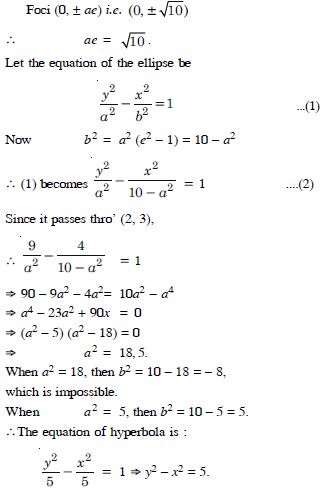NCERT Solutions for Class 11 Math Chapter 11 - Conic Sections

Question 1:

Find an equation of the circle with centre at (0, 0) and radius r.

Question 2:

Find the equation of the circle with centre (–3, 2) and radius 4.

Question 3:

Question 4:

Find the equation of the circle which passes through the points (2, –2) and (3, 4) and whose centre lies on the line x + y = 2.

Question 5:

Find the co-ordinates of the focus, axis, the equation of the directrix and latus-rectum of the parabola y² = 8x.

Question 6:

Find the equation of the parabola with focus (2, 0) and directrix x = – 2.

Question 7:

Find the equation of the parabola with vertex at (0, 0) and focus is (0, 2).

Question 8:

Find the equation of the parabola which is symmetric about y-axis and passes through the point (2, – 3).

Question 9:

Question 10:

Question 11:

Find the equation of the ellipse whose vertices are ($\pm$ 13, 0) and foci are ($\pm$ 5, 0).

Question 12:

Find the equation of the ellipse, whose length of major axis is 20 and foci are (0, $\pm$ 5).

Question 13:

Find the equation of the ellipse, with major axis along the x-axis and passing through the points (4, 3) and (–1, 4).

Question 14:

Find the co-ordinates of the foci and the vertices, the eccentricity, the length of the latus-rectum of the hyperbolas :

Question 15:

Find the co-ordinates of the foci and the vertices, the eccentricity, the length of the latus-rectum of the hyperbolas :

Question 16:

Question 17:

Find the equation of the hyperbola whose foci are (0, $\pm$ 12) and length of the latus-rectum is 36.

Question 18:

The focus of a parabolic mirror as shown in the figure is at a distance of 5 cm from its vertex. If the mirror is 45 cm deep, find the distance AB.

Question 19:

A beam is supported at its end points by supports which are 12 metres apart. Since the load is concentrated at its centre, there is a deflection of 3 cm at the centre and the deflected beam is in the shape of a parabola. How far from the centre is the deflection 1 cm ?

Question 20:

A rod AB of length 15 cm rests in between two co-ordinate axes in such a way that the end point A lies on the x-axis and end point B lies on y-axis. A point P (x, y) is taken on the rod in such a way that AP = 6 cm. Show that the locus of P is an ellipse.

Question 21:

In each of the following, find the equation of the circle with :
Centre (0, 2) and radius 2.

Question 22:

In each of the following, find the equation of the circle with :
Centre (– 2, 3) and radius 4.

Question 23:

In each of the following, find the equation of the circle with :

Question 24:

In each of the following, find the equation of the circle with :

Question 25:

In each of the following, find the equation of the circle with :

Question 26:

In each of the following , find the centre and radius of the circles :

Question 27:

In each of the following , find the centre and radius of the circles :

Question 28:

In each of the following , find the centre and radius of the circles :

Question 29:

In each of the following , find the centre and radius of the circles :

Question 30:

Find the equation of the circle passing through the points (4, 1) and (6, 5) and whose centre is on the line 4x + y = 16.

Question 31:

Find the equation of the circle passing through the points (2, 3) and (– 1, 1) and whose centre is on the line x – 3y – 11 = 0.

Question 32:

Find the equation of the circle of radius 5 whose centre lies on x-axis and passes through the point (2, 3).

Question 33:

Find the equation of the circle passing through (0, 0) and making intercepts a and b on the coordinate axes.

Question 34:

Find the equation of the circle whose centre is (2, 2) and which passes through the point (4, 5).

Question 35:

Question 36:

Find the coordinates of the focus, axis of the parabola, the equation of the directrix and length of latus rectum :
y² = 12x.

Question 37:

Find the coordinates of the focus, axis of the parabola, the equation of the directrix and length of latus rectum x² = 6y.

Question 38:

Find the coordinates of the focus, axis of the parabola, the equation of the directrix and length of latus rectum :
y² = – 8x.

Question 39:

Find the coordinates of the focus, axis of the parabola, the equation of the directrix and length of latus rectum :
x² = – 16y.

Question 40:

Find the coordinates of the focus, axis of the parabola, the equation of the directrix and length of latus rectum :
y² = 10x.

Question 41:

Find the coordinates of the focus, axis of the parabola, the equation of the directrix and length of latus rectum :
x² = – 9y.

Question 42:

Find the equation of the parabola that satisfy the given conditions :
Focus (6, 0), directrix x = – 6.

Question 43:

Find the coordinates of the focus, axis of the parabola, the equation of the directrix and length of latus rectum :
y² = – 8x.

Question 44:

Find the coordinates of the focus, axis of the parabola, the equation of the directrix and length of latus rectum :
x² = – 16y.

Question 45:

Find the coordinates of the focus, axis of the parabola, the equation of the directrix and length of latus rectum :
y² = 10x.

Question 46:

Find the coordinates of the focus, axis of the parabola, the equation of the directrix and length of latus rectum :
x² = – 9y.

Question 47:

Find the equation of the parabola that satisfy the given conditions :
Focus (6, 0), directrix x = – 6.

Question 48:

Find the equation of the parabola that satisfy the given conditions :
Focus (0, – 3), directrix y = 3.

Question 49:

Find the equation of the parabola that satisfy the given conditions :
Vertex (0, 0), focus (3, 0).

Question 50:

Find the equation of the parabola that satisfy the given conditions :
Vertex (0, 0), focus (– 2, 0).

Question 51:

Find the equation of the parabola that satisfy the given conditions :
Vertox (0, 0), passing through (2, 3) and axis is along x-axis.

Question 52:

Find the equation of the parabola that satisfy the given conditions :
Vertex (0, 0), passing through (5, 2) and symmetric with respect to y-axis.

Question 53:

Find the co-ordinates of the foci, the vertices, the length of major axis, the minor axis. the eccentricity and the length of the latus-rectum of the ellipse :

Question 54:

Find the co-ordinates of the foci, the vertices, the length of major axis, the minor axis. the eccentricity and the length of the latus-rectum of the ellipse :

Question 55:

Find the co-ordinates of the foci, the vertices, the length of major axis, the minor axis. the eccentricity and the length of the latus-rectum of the ellipse :

Question 56:

Find the co-ordinates of the foci, the vertices, the length of major axis, the minor axis. the eccentricity and the length of the latus-rectum of the ellipse :

Question 57:

Find the co-ordinates of the foci, the vertices, the length of major axis, the minor axis. the eccentricity and the length of the latus-rectum of the ellipse :

Question 58:

Find the co-ordinates of the foci, the vertices, the length of major axis, the minor axis. the eccentricity and the length of the latus-rectum of the ellipse :

Question 59:

Find the co-ordinates of the foci, the vertices, the length of major axis, the minor axis. the eccentricity and the length of the latus-rectum of the ellipse :
36x² + 4y² = 144.

Question 60:

Find the co-ordinates of the foci, the vertices, the length of major axis, the minor axis. the eccentricity and the length of the latus-rectum of the ellipse :
16x² + y² = 16.

Question 61:

Find the co-ordinates of the foci, the vertices, the length of major axis, the minor axis. the eccentricity and the length of the latus-rectum of the ellipse :

Question 62:

Find the equation for the ellipse that satisfies the given conditions :
Vertices ($\pm$ 5, 0); foci ($\pm$ 4, 0).

Question 63:

Find the equation for the ellipse that satisfies the given conditions :
Vertices (0, $\pm$ 13); foci (0, $\pm$ 5).

Question 64:

Find the equation for the ellipse that satisfies the given conditions :
Vertices ($\pm$ 6, 0); foci ($\pm$ 4, 0).

Question 65:

Find the equation for the ellipse that satisfies the given conditions :
Ends of major-axis ($\pm$ 3, 0); ends of minor axis (0, $\pm$ 2).

Question 66:

Find the equation for the ellipse that satisfies the given conditions :

Question 67:

Find the equation for the ellipse that satisfies the given conditions :
Length of major axis 26; foci ($\pm$ 5, 0).

Question 68:

Find the equation for the ellipse that satisfies the given conditions :
Length of minor-axis 16; foci (0, $\pm$ 6).

Question 69:

Find the equation for the ellipse that satisfies the given conditions :
Foci ($\pm$ 3, 0) ; a = 4.

Question 70:

Find the equation for the ellipse that satisfies the given conditions :
b = 3, c = 4, centre at the origin; focus on x–axis.

Question 71:

Find the equation for the ellipse that satisfies the given conditions :
Centre at (0, 0); major axis on the y–axis and passes through (3, 2) and (1, 6).

Question 72:

Find the equation for the ellipse that satisfies the given conditions :
Major axis on the x–axis and passes through the points (4, 3) and (6, 2).

Question 73:

Find the co-ordinates of the foci and the vertices, the eccentricity and length of the latus-rectum of the hyperbola :

Question 74:

Find the co-ordinates of the foci and the vertices, the eccentricity and length of the latus-rectum of the hyperbola :

Question 75:

Find the co-ordinates of the foci and the vertices, the eccentricity and length of the latus-rectum of the hyperbola :
9y² – 4x² = 36.

Question 76:

Find the co-ordinates of the foci and the vertices, the eccentricity and length of the latus-rectum of the hyperbola :
16x² – 9y² = 576.

Question 77:

Find the co-ordinates of the foci and the vertices, the eccentricity and length of the latus-rectum of the hyperbola :
5y² – 9x² = 36.

Question 78:

Find the co-ordinates of the foci and the vertices, the eccentricity and length of the latus-rectum of the hyperbola :
49y² – 16x² = 784.

Question 79:

Find the equation of the hyperbola satisfying the given conditions :
Vertices ($\pm$ 2, 0); foci ($\pm$ 3, 0).

Question 80:

Find the equation of the hyperbola satisfying the given conditions :
Vertices (0, $\pm$ 5) ; foci (0, $\pm$ 8).

Question 81:

Find the equation of the hyperbola satisfying the given conditions :
Vertices (0, $\pm$ 3) ; foci (0, $\pm$ 5).

Question 82:

Find the equation of the hyperbola satisfying the given conditions :
Foci ($\pm$ 5, 0); the transverse axis is of length 8.

Question 83:

Find the equation of the hyperbola satisfying the given conditions :
Foci (0, $\pm$ 13) ; the conjugate axis is of length 24.

Question 84:

Find the equation of the hyperbola satisfying the given conditions :

Question 85:

Find the equation of the hyperbola satisfying the given conditions :
Foci ($\pm$ 4, 0); the latus-rectum is of length 12.

Question 86:

Find the equation of the hyperbola satisfying the given conditions :

Question 87:

Find the equation of the hyperbola satisfying the given conditions :