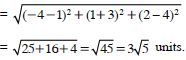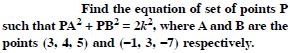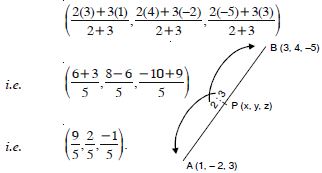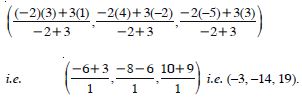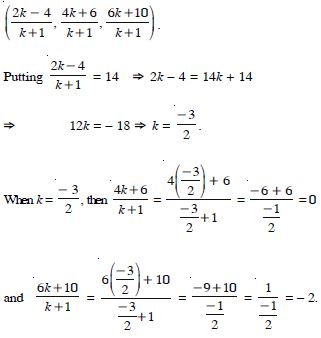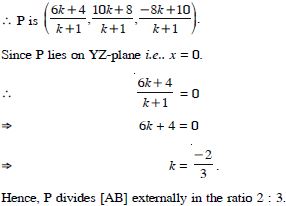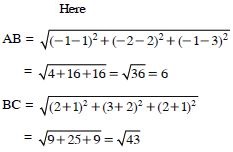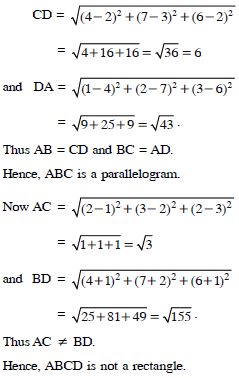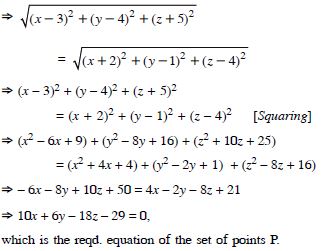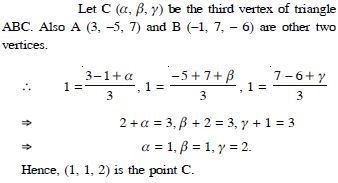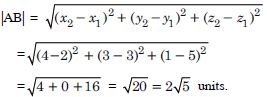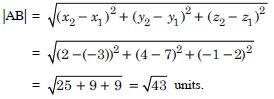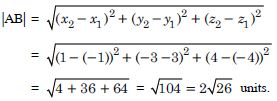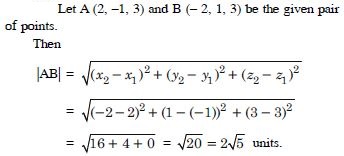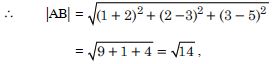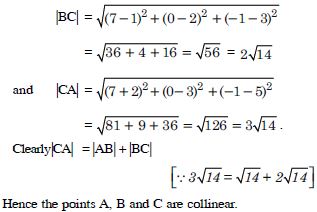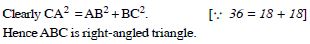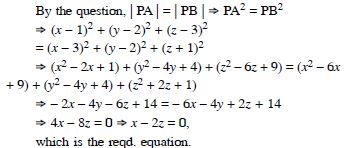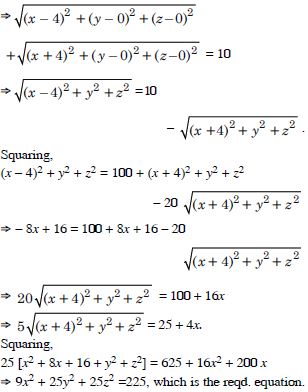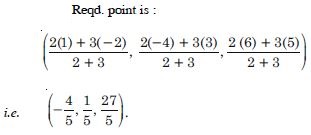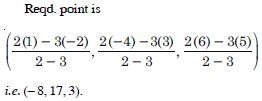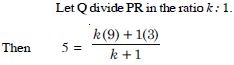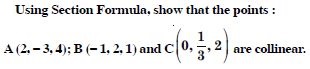Students can refer to the free NCERT Solutions for Class 11 at Aasoka while preparing for the exam. These solutions will clear all concepts related to the chapter “Introduction to Three-Dimensional Geometry”. The NCERT Solutions can be accessed by students anytime and they can study these at their own leisure. The experts have designed the solutions as per the latest CBSE syllabus.
In Maths Class 11 “Introduction to Three-Dimensional Geometry” chapter students will learn about the coordinates of a point, how to find the coordinates of a point in a given space, coordinate planes and coordinate axes in a three-dimension, Cartesian coordinate system, the distance between two points and section formula, and much more.
Question 1:
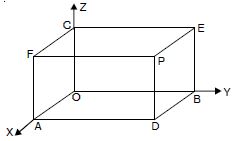
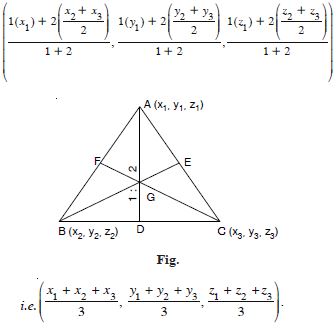
In Fig., if P is (2, 4, 5), find the co-ordinates of F.
Answer:
For the point F, the distance measured along
OY = 0.
Hence, the co-ordinates of F are (2, 0, 5).
Question 2:
Find the octant in which the points (–3, 1, 2) and (–3, 1, –2) lie.
Answer:
The point (–3, 1, 2) lies in second octant.
The point (–3, 1, –2) lies in sixth octant.
Question 3:
Find the distance between the points P(1, –3, 4) are Q(–4, 1, 2).
Answer:
The given points are P(1, –3, 4) and
Q(– 4, 1, 2).
∴ Distance between P and Q = |PQ|
Question 4:
Show that the points P(–2, 3, 5), Q(1, 2, 3) and R(7, 0, –1) are collinear.
Answer:
Question 5:
Are the points A(3, 6, 9), B(10, 20, 30) and C(25, –41, 5), the vertices of a right-angled triangle ?
Answer:
Question 6:
Answer:
Question 7:
Find the co-ordinates of the point, which divides the line segment joining the points (1, –2, 3) and (3, 4, –5) in the ratio 2 : 3 internally
Answer:
Let A(1, –2, 3) and B(3, 4, –5) be the given points.
Let P(x, y, z) be the point, which divides the line segment
[AB] in the ratio 2 : 3.
∴ The co-ordinates of P are :
Question 8:
Find the co-ordinates of the point, which divides the line segment joining the points (1, –2, 3) and (3, 4, –5) in the ratio 2 : 3 externally
Answer:
Let A(1, –2, 3) and B(3, 4, –5) be the given points.
Similarly let Q(x, y, z) be the point, which divides the
line segment [AB] in the ratio – 2 : 3
∴ The co-ordinates of Q are :
Question 9:
Using section formula, prove that the three points (– 4, 6, 10), (2, 4, 6) and (14, 0, –2) are collinear.
Answer:
Let A (– 4, 6, 10) ; B (2, 4, 6) and C (14, 0, – 2) be
the given points.
Let C divide [AB] in the ratio k : 1.
Then the co-ordinates of C are :
Thus C (14, 0, – 2) is a point, which divides [AB]
externally in the ratio 3 : 2.
Hence, A, B and C are collinear.
Question 10:
Answer:
Question 11:
Find the ratio in which the line segment joining the points (4, 8, 10) and (6, 10, –8) is divided by the YZ-plane.
Answer:
Let A(4, 8, 10) and B(6, 10, –8) be the given
points.
Let P(x, y, z) divide the line segment [AB] in the ratio
k : 1.
Question 12:
Show that the points A(1, 2, 3), B(–1, –2, –1) and C(2, 3, 2) and D(4, 7, 6) and the vertices of a parallelogram ABCD, but it is not a rectangle.
Answer:
Question 13:
Find the equation of the set of points P such that its distances from the points A (3, 4, – 5) and B (– 2, 1, 4) are equal.
Answer:
Let P (x, y, z) be any point such that
|PA | = | PB |, where A (3, 4, – 5) and B (– 2, 1, 4) are given
points.
Now | PA | = | PB |
Question 14:
The centroid of a triangle ABC is at the point (1, 1, 1). If the co-ordinates of A and B are (3, – 5, 7) and (–1, 7, – 6) respectively, then find the coordinates of the point C.
Answer:
Question 15:
A point is on x-axis. What are the y-co-ordinate and z-co-ordinate ?
Answer:
Here y-co-ordinate = z-co-ordinate = 0, each.
Question 16:
A point is in the XZ-plane. What can you say about its y-co-ordinate ?
Answer:
y-co-ordinate = 0.
Question 17:
Name the octant in which the following point lie :
(1, 2, 3)
Answer:
Octant I
Question 18:
Name the octant in which the following point lie :
(4, – 2, 3)
Answer:
Octant IV
Question 19:
Name the octant in which the following point lie :
(4, – 2, – 5)
Answer:
Octant VIII
Question 20:
Name the octant in which the following point lie :
(4, 2, – 5)
Answer:
Octant V
Question 21:
Name the octant in which the following point lie :
(– 4, 2, – 5)
Answer:
Octant VI
Question 22:
Name the octant in which the following point lie :
(– 4, 2, 5)
Answer:
Octant II
Question 23:
Name the octant in which the following point lie :
(–3, – 1, 6)
Answer:
Octant III
Question 24:
Name the octant in which the following point lie :
(2, – 4, – 7)
Answer:
Octant VIII
Question 25:
The x-axis and y-axis, taken together, determine a plane, known as ................
Answer:
XY-plane
Question 26:
The co-ordinates of points in the XY-plane are of the form .............
Answer:
(a, b, 0)
Question 27:
Co-ordinate planes divide the space into ............ octants.
Answer:
eight
Question 28:
Find the distance between the following pair of points :
(2, 3, 5) and (4, 3, 1)
Answer:
Let A (2, 3, 5) and B (4, 3, 1) be the given pair of points.
Then
Question 29:
Find the distance between the following pair of points :
(– 3, 7, 2) and (2, 4, – 1)
Answer:
Let A (– 3, 7, 2) and B (2, 4, – 1) be the given pair of points.
Then
Question 30:
Find the distance between the following pair of points :
(– 1, 3, – 4) and (1, –3, 4)
Answer:
Let A (– 1, 3, – 4) and B(1, – 3, 4) be the given pair of points.
Then
Question 31:
Find the distance between the following pair of points :
(2, –1, 3) and (– 2, 1, 3)
Answer:
Question 32:
Show that the points (–2, 3, 5), (1, 2, 3) and (7, 0, – 1) are collinear.
Answer:
Let A(– 2, 3, 5), B (1, 2, 3) and C (7, 0, –1) be the given points.
Question 33:
Verify the following :
(0, 7, –10), (1, 6, –6) and (4, 9, –6) are the vertices of an isosceles triangle.
Answer:
Question 34:
Verify the following :
(0, 7, 10), (–1, 6, 6) and (– 4, 9, 6) are the vertices of a right angled triangle.
Answer:
Question 35:
Verify the following :
(–1, 2, 1), (1, –2, 5), (4, –7, 8) and (2, – 3, 4) are the vertices of a parallelogram.
Answer:
Question 36:
Find the equation of the set of points P, which are equidistant from (1, 2, 3) and (3, 2, – 1).
Answer:
Let A (1, 2, 3) and B (3, 2, – 1) be the given points.
Let P be the point (x, y, z).
Question 37:
Find the equation of the set of points P, the sum of whose distances from A (4, 0, 0) and B (–4, 0, 0) is equal to 10.
Answer:
Let P (x, y, z) be the given point.
By the question,
| PA | + | PB | = 10
Question 38:
Find the co-ordinates of the point, which divides the
line joining the points :
(–2, 3, 5) and (1, –4, 6) in the ratio :
2 : 3 internally
Answer:
Question 39:
Find the co-ordinates of the point, which divides the
line joining the points :
(–2, 3, 5) and (1, –4, 6) in the ratio :
2 : 3 externally
Answer:
Question 40:
Given that P(3, 2, –4), Q (5, 4, –6) and R(9, 8, –10) are collinear. Find the ratio in which Q-divides PR.
Answer:
Question 41:
Find the ratio in which the YZ-plane divides the line segment formed by joining the points (–2, 4, 7) and (3, –5, 8).
Answer:
Question 42:
Answer:
Question 43:
Find the co-ordinates of the points, which trisect the line segment joining the points P (4, 2, – 6) and Q (10, – 16, 6).