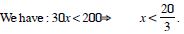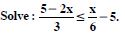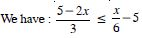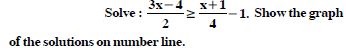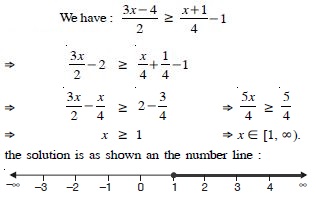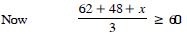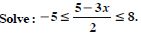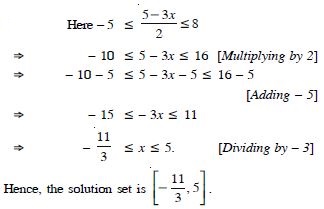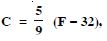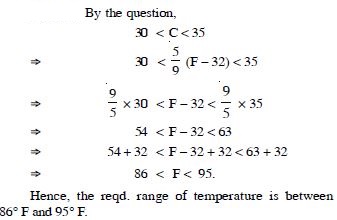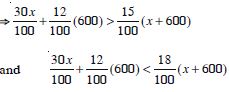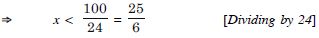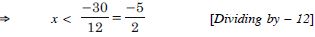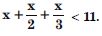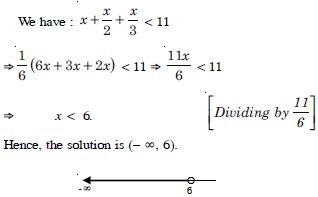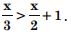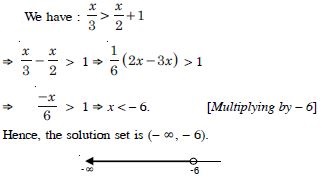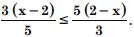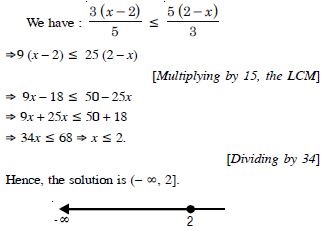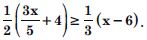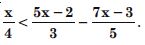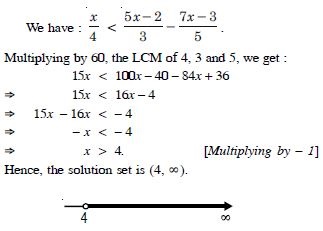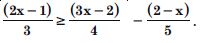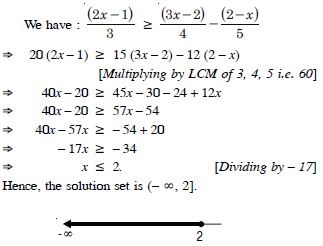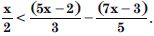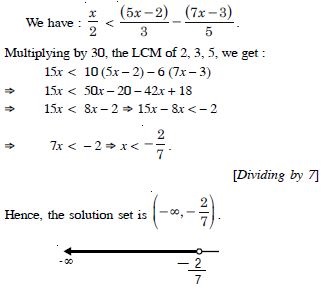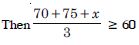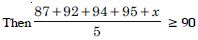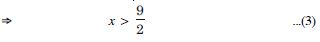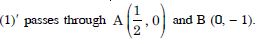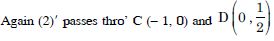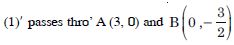Class 11 students can access free NCERT Solutions online at Aasoka. These solutions will help clear all concepts and doubts related to the chapter “Linear Inequalities”. The NCERT Solutions for Class 11 includes top-quality content written as per the latest CBSE syllabus and guidelines. Students can enhance their overall performance to score excellent marks in their exams. So, get on with the exam preparations now.
In the chapter “Linear Inequalities” of Maths Class 11, students will learn about the graphical representation of the solution of the system of linear inequalities in two variables, linear inequalities, graphical solution of linear inequalities in two variables, algebraic solutions of linear inequalities in one variable, representation of solutions on the number line, and much more.
Question 1:
Solve : 30x < 200 when :
x is a natural number
Answer:
Solution set is {1, 2, 3, 4, 5, 6}.
Question 2:
Solve : 30x < 200 when :
x is an integer
Answer:
Solution set is {....... –3, –2, –1, 0, 1, 2, 3, 4, 5, 6}.
Question 3:
Solve : 5x – 3 < 3x + 1 when :
x is an integer
Answer:
We have : 5x – 3 < 3x + 1
5x – 3 + 3 < 3x + 1 + 3 5x < 3x + 4
5x – 3x < 3x + 4 – 3x 2x < 4
x < 2.
Solution set is {......... – 3, –2, –1, 0, 1}.
Question 4:
Solve : 5x – 3 < 3x + 1 when :
x is a real number
Answer:
We have : 5x – 3 < 3x + 1
5x – 3 + 3 < 3x + 1 + 3 5x < 3x + 4
5x – 3x < 3x + 4 – 3x 2x < 4
x < 2.
Solution set is (–, 2).
Question 5:
Solve : 4x + 3 < 6x + 7.
Answer:
We have : 4x + 3 < 6x + 7
4x + 3 – 3 < 6x + 7 – 3
4x < 6x + 4 4x – 6x < 6x + 4 – 6x
– 2x < 4 x > – 2.
Hence, the solution set is (– 2, ).
Question 6:
Answer:
2(5 – 2x) x – 30 [Multiplying both sides by 6]
10 – 4x x – 30
– 5x – 40 x 8.
Hence, the solution set is [8, ).
Question 7:
Solve : 7x + 3 < 5x + 9. Show the graph of the solution on number line.
Answer:
We have : 7x + 3 < 5x + 9
2x < 6 x < 3.
Hence, the solution set is (– , 3),
which is shown on the number line as below :
Question 8:
Answer:
Question 9:
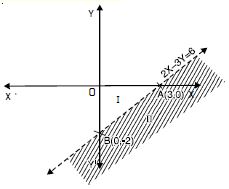
Find all pairs of consecutive odd natural numbers, both of which are larger than 10, such that their sum is less than 40.
Answer:
Let ‘x’ be the smaller of two consecutive odd natural
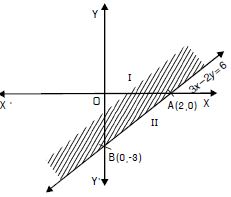
numbers. Then the larger number = x + 2.
By the question, x > 10 ...(1)
and x + (x + 2) < 40 ...(2)
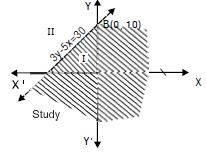
From (2), 2x + 2 < 40
2x < 38
x < 19 ...(3)
Combining (1) and (3), 10 < x < 19.
Hence, the possible pairs are (11, 13), (13, 15), (15, 17) and
(17, 19).
Question 10:
The marks obtained by a student in first terminal and second terminal are 62 and 48. Find the number of minimum marks he should get in the annual examination to have an average of atleast 60 marks.
Answer:
Let ‘x’ be the marks in the annual examination.
110 + x 180
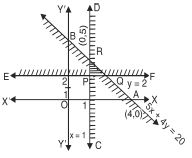
x 70.
Hence, the number of minimum marks = 70.
Question 11:
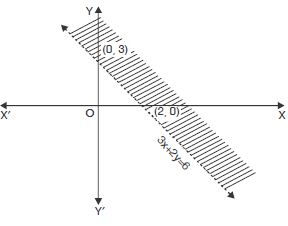
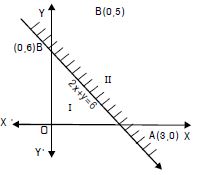
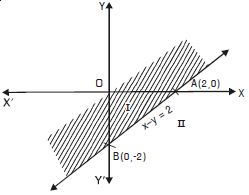
Solve : 3x + 2y > 6 graphically.
Answer:
The given inequation is 3x + 2y > 6 ...(1)
The corresponding equation is 3x + 2y = 6.
This meets x-axis at (2, 0) and y-axis at (0, 3).
Joining these points, we get the straight line 3x + 2y = 6.
Clearly the plane is divided into two regions.
Take (0, 0) as an arbitrary point.
Putting in (1), 0 + 0 > 6 i.e. 0 > 6, which is not true.
O(0, 0) does not lie on the graph.
Hence, each part in the shaded region (excluding all points
on the line) determines the solution.
Question 12:
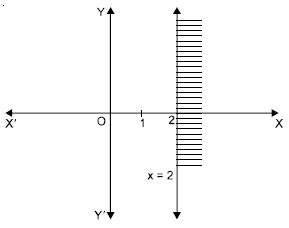
Solve 3x – 6 0 graphically in twodimensional space.
Answer:
We have : 3x – 6 0 ...(1)
Converting it into an equation, we get :
3x – 6 = 0 3x = 6
x = 2.
Clearly it is a st. line parallel to y-axis at a distance of
2 units on the right of origin. This divides the xy-plane into
two parts.
Select the arbitrary point ; say (0, 0).
This does not satisfy (1). [_ 0 2 is not true]
Thus the shaded region is the required solution set.
Hence, each point on the RHS of the line (including all
points on the line) determines the solution of the given
inequation.
Question 13:
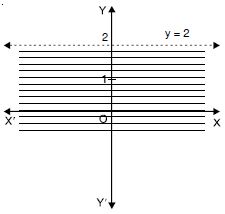
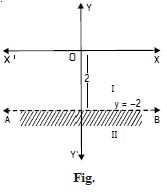
Solve : y < 2 graphically.
Answer:
We have : y < 2 ...(1)
Converting it into an equation, we get : y = 2.
Clearly it is a st. line parallel to x-axis at a distance of
2 units above the origin.
This divides the XY-plane into two parts.
Select the arbitrary point ; say (0, 0).
This does not satisfy (1) [_ 0 < 2 is not true] Thus the shaded region is the required
solution set.
Hence, each point below the line (excluding all points on
the line) determines the solution of the given inequation.
Question 14:
Solve the following system of linear
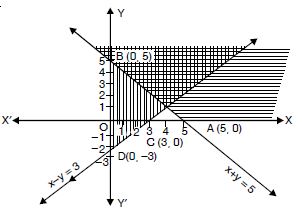
inequations :
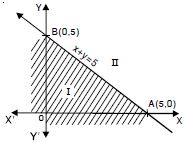
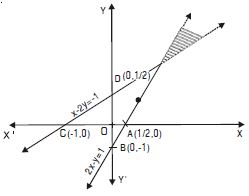
x + y 5 and x – y 3.
Answer:
The given inequations are x + y 5 ...(1)
and x – y 3 ...(2)
The graph of the equation x + y = 5 is the line joining the
points A (5, 0) and B (0, 5).
The solution of the inequation (1) is represented by the
shaded region away from the origin (including points as
the line).
The graph of the equation x – y = 3 is the line joining the
points C(3, 0) and D(0, –3)
The solution of the inequation (2) is represented by the
shaded region towards the origin including the points on the
line.
Hence, the double shaded region, common to (1)
and (2) is the required solution.
Question 15:
Solve the following system of inequalities
graphically :
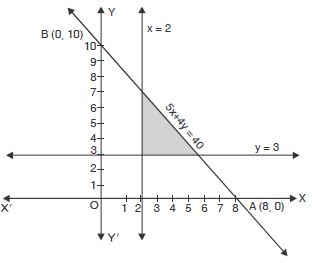
5x + 4y 40, x 2, y 3.
Answer:
The given inequalities are :
5x + 4y 40 ...(1)
x 2 ...(2)
and y 3 ...(3)
Let us draw the graphs of 5x + 4y = 40, x = 2 and y = 3.
The st. line 5x + 4y = 40 passes through (8, 0) and
(0, 10).
Let AB be this line
Shaded portion is towards the origin.
x = 2 and y = 3 are also shown.
Hence, the feasible region (shown shaded) is the required
solution set.
Question 16:
Solve the following system of inequalities :
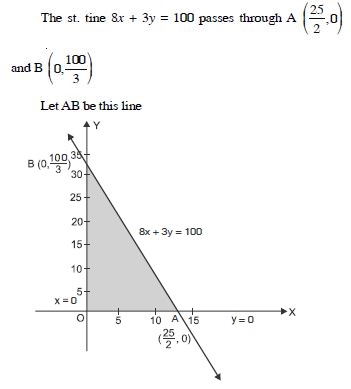
8x + 3y 100, x 0, y 0.
Answer:
The given inequalities are :
8x + 3y 100 ...(1)
x 0 ...(2)
and y 0 ...(3)
Draw the graph of 8x + 3y = 100.
The shaded portion is towards the origin.
x = 0 and y = 0 are also shown.
Hence, the feasible region (shown shaded) is the required
solution set.
Question 17:
Solve the following system of inequalities
graphically :
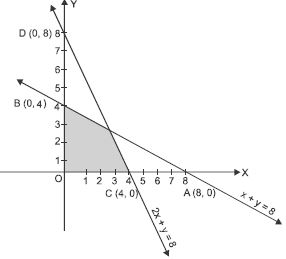
x + 2y 8, 2x + y 8, x 0, y 0.
Answer:
We have : x + 2y 8 ...(1)
2x + y 8 ...(2)
x 0, y 0 ...(3)
Draw the lines x + 2y = 8, 2x + y = 8 and x = 0, y = 0.
The line x + 2y = 8 meets x = axis at A (8, 0)
and y-axis at B(0, 4),
This is the line AB.
Shaded portion is towards the origin.
The line 2x + y = 8 meets x-axis at C(4, 0)
and y-axis at (0, 8).
This is the line CD.
Shaded portion is towards the origin.
x = 0, y = 0 are also shown.
Hence, the feasible region (shown shaded) is the required solution set.
Question 18:
Solve : – 8 5x – 3 < 7.
Answer:
Here – 8 5x – 3 < 7
– 8 + 3 5x – 3 + 3 < 7 + 3 [Adding 3]
– 5 5x < 10
– 1 x < 2. [Dividing by 5]
Hence, the solution set is [– 1, 2). < Here – 8 5x – 3 < 7
– 8 + 3 5x – 3 + 3 < 7 + 3 [Adding 3]
– 5 5x < 10
– 1 x < 2. [Dividing by 5]
Hence, the solution set is [– 1, 2)./p>
Question 19:
Answer:
Question 20:
Solve the system of inequalities :
3x – 7 < 5 + x, 11 – 5x 1.
Answer:
Question 21:
In an experiment, a solution of hydrochloric acid is to be kept between 30 and 35 Celsius. What is the range of temperature in degree Fahrenheit if conversion formula is given by :
where C and F represent temperature in degree Celsius and degree Fahrenheit respectively.
Answer:
Question 22:
A manufacturer has 600 litres of a 12% solution of acid. How many litres of a 30% acid solution must be added to it so that acid content in the resulting mixture will be more than 15% but less than 18% ?
Answer:
Let ‘x’ be the number of litres of 30% acid
solution.
Then total mixture = (x + 600) litres.
By the question,
30% of x + 12% of (600) > 15 of (x + 600)
and 30% of x + 12% of (600) < 18 of (x + 600)
30x + 7200 > 15x + 9000
and 30x + 7200 < 18x + 10800
15x > 1800 and 12x < 3600
x > 120 and x < 300
120 < x < 300.
Hence, the number of litres of 30% solution of acid will
have to be more than 120 but less than 300.
Question 23:
Solve : 24x < 100, when :
x is a natural number
Answer:
We have : 24x < 100 ...(1)
Hence, (1) is true when :
Solution set is {1, 2, 3, 4}.
Question 24:
Solve : 24x < 100, when :
x is an integer.
Answer:
We have : 24x < 100 ...(1)
Hence, (1) is true when :
Solution set is
{............ – 3, – 2, – 1, 0, 1, 2, 3, ...............}.
Question 25:
Solve : – 12x > 30, when :
x is a natural number
Answer:
We have : – 12x > 30 ...(1)
Hence, (1) is true when :
Solution set is i.e. there is no solution.
Question 26:
Solve : – 12x > 30, when :
x is an integer
Answer:
We have : – 12x > 30 ...(1)
Hence, (1) is true when :
Solution set is {............, – 4, – 3}.
Question 27:
Solve : 5x – 3 < 7, when :
x is an integer
Answer:
We have : 5x – 3 < 7
5x < 7 + 3
[Adding 3 on both sides]
5x < 10 x < 2.
[Dividing by 2]
The solution set is {........ – 2, – 1, 0, 1}.
Question 28:
Solve : 5x – 3 < 7, when :
x is a real number
Answer:
We have : 5x – 3 < 7
5x < 7 + 3
[Adding 3 on both sides]
5x < 10 x < 2.
[Dividing by 2]
The solution set is (– , 2).
Question 29:
Solve : 3x + 8 > 2, when :
x is an integer
Answer:
We have : 3x + 8 > 2
3x > 2 – 8
3x > – 6
x > – 2. [Dividing by 2]
The solution set is {– 1, 0, 1, 2, 3, ........}.
Question 30:
Solve : 3x + 8 > 2, when :
x is a real number
Answer:
We have : 3x + 8 > 2
3x > 2 – 8
3x > – 6
x > – 2. [Dividing by 2]
The solution set is (– 2, ).
Question 31:
Solve the inequalities for real x :
4x + 3 < 6x + 7.
Answer:
We have : 4x + 3 < 6x + 7
4x – 6x < 7 – 3 – 2x < 4.
Dividing by – 2, x > – 2.
Hence, the solution set is (– 2, ).
Question 32:
Solve the inequalities for real x :
3x – 7 > 5x – 1.
Answer:
We have : 3x – 7 > 5x – 1
3x – 5x > 7 – 1 – 2x > 6
Dividing by – 2, x < – 3.
Hence, the solution set is (– , – 3).
Question 33:
Solve the inequalities for real x :
3 (x – 1) 2 (x – 3).
Answer:
We have : 3 (x – 1) 2 (x – 3)
3x – 3 2x – 6 3x – 2x – 6 + 3
x – 3.
Hence, the solution set is (– , – 3]
Question 34:
Solve the inequalities for real x :
3 (2 – x) 2 (1 – x).
Answer:
We have : 3 (2 – x) 2 (1 – x)
6 – 3x 2 – 2x – 3x + 2x 2 – 6
– x – 4 x 4
[Dividing by – 1]
Hence, the solution set is (– , 4].
Question 35:
Solve the inequalities for real x :
Answer:
Question 36:
Solve the inequalities for real x :
Answer:
Question 37:
Solve the inequalities for real x :
Answer:
Question 38:
Solve the inequalities for real x :
Answer:
Question 39:
Solve the inequalities for real x :
2 (2x + 3) – 10 < 6 (x – 2).
Answer:
We have : 2 (2x + 3) – 10 < 6 (x – 2)
4x + 6 – 10 < 6x – 12 4x – 4 < 6x – 12
4x – 6x < 4 – 12 – 2x < – 8
x > 4. [Dividing by – 2]
Hence, the solution set is (4, ).
Question 40:
Solve the inequalities for real x :
37 – (3x + 5) 9x – 8 (x – 3).
Answer:
We have : 37 – (3x + 5) 9x – 8 (x – 3)
37 – 3x – 5 9x – 8x + 24
32 – 3x x + 24 – 3x – x 24 – 32
– 4x – 8 x 2. [Dividing by – 4]
Hence, the solution set is (– , 2].
Question 41:
Solve the inequalities for real x :
Answer:
Question 42:
Solve the inequalities for real x :
Answer:
Question 43:
Solve the inequalities and show the graph of
the solution in each case on number line :
3x – 2 < 2x + 1.
Answer:
We have : 3x – 2 < 2x + 1
3x – 2x < 1 + 2 x < 3.
Hence, the solution set is (– , 3).
Question 44:
Solve the inequalities and show the graph of
the solution in each case on number line :
5x – 3 3x – 5.
Answer:
We have : 5x – 3 3x – 5
5x – 3x 3 – 5
2x – 2
x – 1. [Dividing by 2]
Hence, the solution set is [– 1, ).
Question 45:
Solve the inequalities and show the graph of
the solution in each case on number line :
3 (1 – x) < 2 (x + 4).
Answer:
We have : 3 (1 – x) < 2 (x + 4)
3 – 3x < 2x + 8 – 3x – 2x < 8 – 3
– 5x < 5 x > – 1.
[Dividing by – 1]
Hence, the solution set is (– 1, ).
Question 46:
Solve the inequalities and show the graph of the solution in each case on number line :
Answer:
Question 47:
Ravi obtained 70 and 75 marks in first two unit tests. Find the number of minimum marks he should get in the third test to have an average of at least 60 marks.
Answer:
Let ‘x’ be the marks obtained by Ravi in the third test.
145 + x 180
x 35.
Hence, Ravi must obtain a minimum of 35 marks to get an
average of at least 60 marks.
Question 48:
To receive Grade ‘A’ in a course, one must obtain an average of 90 marks or more in five examinations (each of 100 marks). If Sunita’s marks in first four examinations are 87, 92, 94, and 95, find the minimum marks that Sunita must obtain in fifth examination to get grade ‘A’ in the course.
Answer:
Let Sunita obtain ‘x’ marks in the fifth examination.
368 + x 450 x 82.
Hence, minimum marks that Sunita must obtain = 82.
Question 49:
Find all pairs of consecutive odd positive integers, both of which are smaller than 10 such that their sum is more than 11.
Answer:
Let ‘x’ be the smaller of two consecutive positive
integers. Then the other number = x + 2.
By the question, x < 10 ...(1)
and x + (x + 2) > 11 ...(2)
From (2), 2x + 2 > 11 2x > 9
If one number is 5, then the other is 7.
If one number is 7, then the other is 9.
Hence, the possible pairs are (5, 7), (7, 9).
Question 50:
Find all pairs of consecutive even positive numbers, both of which are larger than 5 such that their sum is less than 23.
Answer:
Let ‘x’ be the smaller of the two positive even
numbers,
Then the other number is x + 2.
By the question,
x > 5 ...(1)
and x + (x + 2) < 23
i.e. 2x + 2 < 23 ...(2)
If the sum is less than 23, then it is also less than 24,
2x + 2 < 24 2x < 22
x < 11.
Thus x may be 6, 8, 10.
Hence, the possible pairs are (6, 8), (8, 10) and (10, 12).
Question 51:
The longest side of a triangle is 3 times the shortest side and the third side is 2 cm shorter than the longest side. If the perimeter of the triangle is at least 61 cm, find the minimum length of the shortest side.
Answer:
Let ‘x’ be the shortest side.
Then longest side = 3x and third side = 3x – 2.
Now x + 3x + (3x – 2) 61
7x 63
x 9.
Hence, the minimum length of the shortest side = 9 cm.
Question 52:
A man wants to cut three lengths from a single piece of board of length 91 cm. The second length is to be 3 cm longer than the shortest and third length is to be thrice as long as the shortest. What are the possible lengths for the shortest board if the third piece is to be at least 5 cm longer than the second ?
Answer:
Let ‘x’ be the length of the shortest board.
Then second length = x + 3
and third length = 2x.
By the question,
2x (x + 3) + 5
x 8 ...(1)
Also x + (x + 3) + 2x 91
4x 88 x 22 ...(2)
From (1) and (2),
8 x 22.
Hence, the shortest board is at least 8 cm long but not
more than 22 cm long.
Question 53:
Solve the following inequalities graphically in two dimensional plane :
x + y 5.Answer:
The given inequality is x + y < 5 ... (1)
The corresponding equation is x + y = 5 ...(2)
This passes through the points A (5, 0) and B (0, 5).
(2) represents the line AB.
Putting x = 0, y = 0 in (1), we get :
0 + 0 < 5 i.e. 0 < 5,
which is true.
Hence, half-plane I is the solution region of the given
inequality.
Question 54:
Solve the following inequalities graphically in two
dimensional plane :
2x + y 6.
Answer:
The given inequality is 2x + y 6 ...(1)
The corresponding equation is 2x + y = 6 ...(2)
This passes through the points A (3, 0) and B (0, 6).
(2) represent the line AB.
Putting x = 0, y = 0 in (1) we get :
0 + 0 6 i.e. 0 6, which is not true.
Hence, half-Plane – II is the solution region of the given
inequality.
Question 55:
Solve the following inequalities graphically in two
dimensional plane :
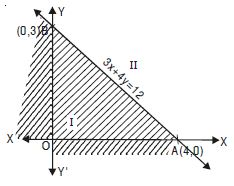
3x + 4y 12.
Answer:
The given inequality is 3x + 4y 12 ...(1)
The corresponding equation is 3x + 4y = 12 ...(2)
This passes through the points A (4, 0) and B (0, 3).
(2) represents the line AB.
Putting x = 0, y = 0 in (1), we get :
0 + 0 12, which is true.
Hence, half-plane I is the solution region of the given
inequality.
Question 56:
Solve the following inequalities graphically in two
dimensional plane :
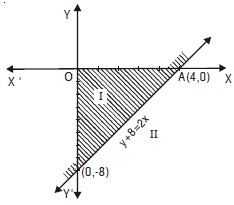
y + 8 2x.
Answer:
The given inequality is y + 8 2x ...(1)
The corresponding equation is y + 8 = 2x ...(2)
This passes through the points A (4, 0) and B (0, – 8).
(2) represents the line AB.
Putting x = 0, y = 0 in (1), we get :
0 + 8 0 i.e. 8 0,
which is true.
Hence, half-plane I is the solution region of the given inequality.
Question 57:
Solve the following inequalities graphically in two
dimensional plane :
x – y 2.
Answer:
The given inequality is x – y 2 ...(1)
The corresponding equation is x – y = 2 ...(2)
This passes through A (2, 0) and B (0, – 2)
(2) represents the line AB.
Putting x = 0, y = 0 in (1)
0 – 0 2 0 < 2, which is true.
Hence, half-plane I is the solution region of the given
inequality.
Question 58:
Solve the following inequalities graphically in two
dimensional plane :
2x – 3y > 6
Answer:
The given inequality is 2x – 3y > 6 ...(1)
The corresponding equation is 2x – 3y = 6 ...(2)
This passes through A (3, 0) and B (0, – 2)
(2) represents the line AB.
Putting x = 0, y = 0 in (1), we get :
0 – 0 > 6 i.e. 0 > 6, which is not true.
Hence, half-plane II is the solution region of the given
inequality.
Question 59:
Solve the following inequalities graphically in two
dimensional plane :
– 3x + 2y – 6.
Answer:
The given inequality is – 3x + 2y – 6 ...(1)
The corresponding equation is
– 3x + 2y = – 6
i.e. 3x – 2y = 6 ...(2)
This passes through A (2, 0) and B (0, – 3).
(2) represents the line AB.
Putting x = 0, y = 0 in (1) we get :
– 0 + 0 – 6 i.e. 0 – 6,
which is true.
Hence, half-plane I is the solution region of the given
inequality.
Question 60:
Solve the following inequalities graphically in two
dimensional plane :
3y – 5x < 30.
Answer:
The given inequality is 3y – 5x < 30 ...(1)
The corresponding equation is 3y – 5x = 30 ...(2)
This passes through A (– 6, 0) and B (0, 10).
(2) represents the line AB.
Putting x = 0, y = 0 in (1), we get
0 – 0 < 30 i.e. 0 < 30, which is true.
Hence, half plane I is the solution region of the given
inequality.
Question 61:
Solve the following inequalities graphically in two
dimensional plane :
y < – 2.
Answer:
The given inequality is y < – 2 ...(1)
The corresponding equation is y = – 2 ...(2)
This represents the line AB
Putting x = 0, y = 0 in (1), 0 < – 2, which is not true.
Hence, half-plane II is the solution region of the given
inequality.
Question 62:
Solve the following inequalities graphically in two
dimensional plane :
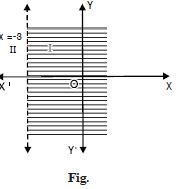
x > – 3.
Answer:
The given inequality is x > – 3 ...(1)
The corresponding equation is x = – 3 ...(2)
This represents the line AB.
Putting x = 0, y = 0 in (1)
0 > – 3, which is true.
Hence, half-plane I is the solution region of the given inequality.
Question 63:
Solve the following system of inequalities graphically :
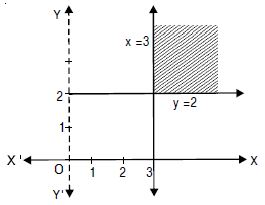
x 3, y 2.
Answer:
x 3 represents the region on the right
side of x = 3 including x = 3,
y 2 represents the region above y = 2 including y = 2.
Any point in this region is the solution of x 3, y 2.
Question 64:
Solve the following system of inequalities graphically :
3x + 2y 12, x 1, y 2.
Answer:
Let us draw the graphs of 3x + 2y = 12, x = 1, y = 2.
The st. line 3x + 2y = 12 passes through (4, 0) and (0, 6).
Let AB be this line.
Shaded portion is towards the origin.
[_ 0 12 is true]
x = 1, y = 2, are also shown.
Hence, the feasible region (shown shaded) is the solution
set of the given system of inequations.
Question 65:
Solve the following system of inequalities graphically :
2x + y 6, 3x + 4y 12.
Answer:
The given inequalities are :
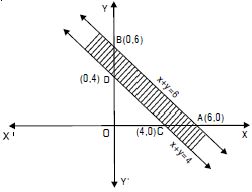
2x + y 6 ....(1)
and 3x + 4y 12 ....(2)
The corresponding equations are :
2x + y = 6 ....(1)′
and 3x + 4y = 12 ....(2)′
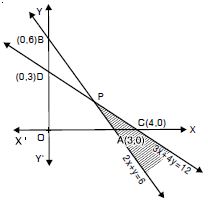
(1)′ passes through A (3, 0) and B (0, 6).
(1)′ represents the line AB.
(2)′ passes through C (4, 0) and D (0, 3).
(2)′ represents the line CD.
Putting x = 0, y = 0 in (1),
0 + 0 6 i.e. 0 6, which is not true.
Origin does not lie in this region.
The region lying above AB and all points on AB
represents (1).
Again putting x = 0, y = 0, in (2),
0 + 0 12 i.e. 0 12, which is true.
The region lying below CD (towards origin) and all
points lying on CD.
Hence, the common region (shown shaded) is the solution
of (1) and (2).
Question 66:
Solve the following system of inequalities graphically :
x + y > 4, 2x – y > 0.
Answer:
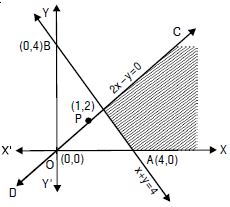
The given inequalities are
x + y > 4 ....(1)
and 2x – y > 0 ....(2)
The corresponding equations are
x + y = 4 ....(1)′
and 2x – y = 0 ....(2)′
(1)′ passes through A (4, 0) and B (0, 4)
(1)′ represents the line AB.
Putting x = 0, y = 0 in (1) 0 + 0 > 4 i.e. 0 > 4, which is not
true.
Origin does not lie in the region
The line 2x – y = 0 passes thro’ O (0, 0) and P (1, 2).
This represents the line CD.
Putting x = 1, y = 0 in (2) 0 > 0, which is true.
(1, 0) lies in the region.
The common region is shown as shaded in the figure.
Question 67:
Solve the following system of inequalities graphically :
2x – y > 1, x – 2y < – 1.
Answer:
The given inequalities are :
2x – y > 1 ....(1)
and x – 2y < – 1 ....(2)
The corresponding equations are :
2x – y = 1 ...(1)′
and x – 2y = – 1 ...(2)′
(1)′ represents the line AB.
Putting x = 0, y = 0 in (1), 0 – 0 > 1
i.e. 0 > 1, which is not true.
Origin does not lie in the region.
(2)′ represents the line CD.
Putting x = 0, y = 0 in (2), 0 – 0 < – 1
i.e. 0 < – 1, which is not true.
Origin does not lie in the region.
The common region is as shown shaded in the figure.
Question 68:
Solve the following system of inequalities graphically :
x + y 6, x + y 4.
Answer:
The given inequalities are :
x + y 6 ....(1)
and x + y 4 ....(2)
The corresponding equations are :
x + y = 6 ....(1)′
and x + y = 4 ....(2)′
(1)′ passes thro’ A (6, 0) and B (0, 6).
(1)′ represents the line AB.
Putting x = 0, y = 0 in (1), 0 + 0 6
i.e. 0 6, which is true.
Origin lies in the region.
Again (2)′ passes thro’ C (4, 0) and D (0, 4).
(2)′ represents the line CD.
Putting x = 0, y = 0 in (2), 0 + 0 4
i.e. 0 4, which is not true.
Origin does not lie in the region.
The common region is shown as shaded in the figure.
Question 69:
Solve the following system of inequalities graphically :
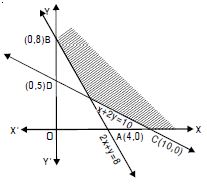
2x + y 8, x + 2y 10.
Answer:
The given inequalities are
2x + y 8 ....(1)
and x + 2y 10 ....(2)
The corresponding equations are
2x + y = 8 ....(1)′
and x + 2y = 10 ....(2)′
(1)′ passes thro’ A (4, 0) and B (0, 8).
(1)′ represents the line AB.
Putting x = 0, y = 0 in (1), 0 + 0 8
i.e. 0 8, which is not true.
Origin does not lie in the region.
Again (2)′ passes thro’ C (10, 0) and D (0, 5).
(2)′ represents the line CD.
Putting x = 0, y = 0 in (2), 0 + 0 10 i.e. 0 10,
which is not true.
Origin does not lie in the region.
The common region is shown as shaded in the figure.
Question 70:
Solve the following system of inequalities graphically :
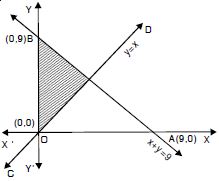
x + y 9, y > x, x 0.
Answer:
The given inequalities are
x + y 9 ....(1)
y > x ....(2)
and x 0 ....(3)
The corresponding equation of (1) is
x + y = 9 ....(1)′
(1)′ passes thro’ A (9, 0) and B (0, 9).
(1)′ represents the line AB.
Putting x = 0, y = 0 in (1), 0 + 0 9
i.e. 0 9, which is true.
Origin lies in the region.
Now corresponding equation of (2) is y = x.
This passes through (0, 0), (1, 1).
(2)′ represents the line CD.
Putting x = 0, y = 1 in (2), y > x
i.e. y – x > 0,
1 – 0 > 0 i.e. 1 > 0, which is true.
(0, 1) lies in the region
Lastly x > 0 represents the right of y-axis.
The common region is shown as shaded in the figure.
Question 71:
Solve the following system of inequalities graphically :
5x + 4y 20, x 1, y 2.
Answer:
Let us draw the graphs of 5x + 4y = 20, x = 1, y = 2.
The st. line 5x + 4y = 20 passes through (4, 0) and (0, 5).
Let AB be this line.
Shaded portion is towards the origin
[∵ 0 20 is true]
Region above y = 2 represents the inequality y 2
including the points on the line. Region on the right of x = 1
represents the inequality x 1, including the points on the
line. The double shaded area bounded by ΔPQR is the
required solution.
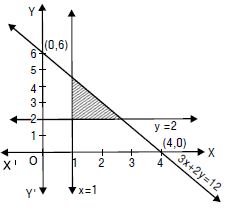
Question 72:
Solve the following system of inequalities graphically :
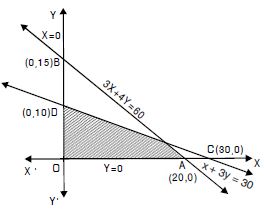
3x + 4y 60, x + 3y 30, x 0 y 0.
Answer:
The given inequalities are
3x + 4y 60 ....(1)
x + 3y 30 ....(2)
and x 0, y 0 ....(3)
The corresponding equations are
3x + 4y = 60 ....(1)′
x + 3y = 30 ....(2)′
and x = 0, y = 0 ....(3)′
(1)′ passes thro’ A (20, 0) and B (0, 15).
(1)′ represents the line AB.
Putting x = 0, y = 0 in (1), 0 + 0 60
i.e. 0 60, which is true.
Origin lies in the region.
Again (2)′ passes through C (30, 0) and
D (0, 10).
(2)′ represents the line CD.
Putting x = 0, y = 0 in (2), 0 + 0 30
i.e. 0 30, which is true.
Origin lies in the region.
Now x 0 is the region on and right of y-axis.
And y 0 is the region on and above of x-axis
The common region is shown as shaded in the figure.
Question 73:
Solve the following system of inequalities graphically :
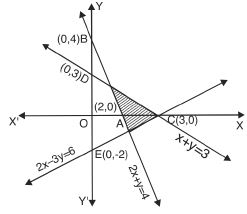
2x + y 4, x + y 3, 2x – 3y 6.
Answer:
The given inequalities are :
2x + y 4 ....(1)
x + y 3 ....(2)
and 2x – 3y 6 ....(3)
The corresponding equations are :
2x + y = 4 ....(1)′
x + y = 3 ....(2)′
and 2x – 3y = 6 ....(3)′
(1)′ passes thro’ A (2, 0) and B (0, 4).
(1)′ represents the line AB.
Putting x = 0, y = 0 in (1), 0 + 0 4 i.e. 0 4, which is not
true.
Origin does not lie in the region.
(2)′ passes thro’ C (3, 0) and D (0, 3).
(2)′ represents the line CD.
Putting x = 0, y = 0 in (2), 0 + 0 3 i.e. 0 3, which is
true.
Origin lies in the region.
(3)′ passes through C (3, 0) and E (0, – 2)
(3)′ represents the line CE.
Putting x = 0, y = 0 in (3) 0 – 0 6 i.e. 0 6, which is
true.
Origin lies in the region.
The common region is shown as shaded in the figure.
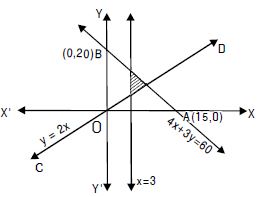
Question 74:
Solve the following system of inequalities graphically :
x – 2y 3, 3x + 4y 12, x 0 y 0.
Answer:
The given inequalities are
x – 2y 3 ...(1)
3x + 4y 12 ...(2)
and x 0, y 1 ...(3)
The corresponding equations are
x – 2y = 3 ...(1)′
3x + 4y = 12 ...(2)′
and x = 0, y = 1 ...(3)′
(1)′ represents the line AB.
Putting x = 0, y = 0 in (1), 0 – 0 3 i.e. 0 3, which is
true.
Origin lies in the region.
(2)′ passes thro’ C (4, 0) and D (0, 3).
(2)′ represents the line CD.
Putting x = 0, y = 0 in (2), 0 + 0 12 i.e. 0 12, which is
not true.
Origin does not lies in the region.
Now x 0 represents y-axis and right of y-axis.
And y 1 represents the line y = 1 and above it.
The common region is shown as shaded in the figure.
Question 75:
Solve the following system of inequalities graphically :
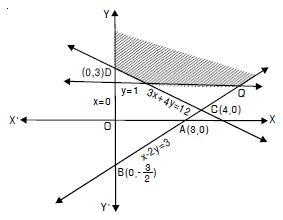
4x + 3y 60, y 2x, x 3, x, y 0.
Answer:
The given inequalities are
4x + 3y 60 ...(1)
y 2x ...(2)
x 3 ...(3)
and x, y 0 ...(4)
The corresponding equations are
4x + 3y = 60 ...(1)′
y = 2x ...(2)′
x = 3 ...(3)′
(1)′ passes thro’ A (15, 0) and B (0, 20).
(1)′ represents the line AB.
Putting x = 0, y = 0 in (1), 0 + 0 60 i.e. 0 60, which is
true.
Origin lies in the region.
Now y = 2x passes thro’ O (0, 0) and (5, 10).
(2)′ represents the line CD.
Putting x = 0, y = 5 in (2), 5 0,
which is true.
(0, 5) lies in the region.
x 3 represents the line x = 3 and right of it.
x, y 0 represents the region in first quadrant.
The common region is shown as shaded in the figure.
Question 76:
Solve the following system of inequalities graphically :
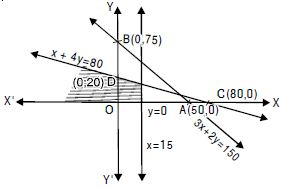
3x + 2y 150, x + 4y 80, x 15, y 0.
Answer:
The given inequalities are
3x + 2y 150 ...(1)
x + 4y 80 ...(2)
x 15 ...(3)
y 0 ...(4)
The corresponding equations are
3x + 2y = 150 ...(1)′
x + 4y = 80 ...(2)′
x = 15 ...(3)′
and y = 0 ...(4)′
(1)′ passes thro’ A (50, 0) and B (0, 75).
(1)′ represents the line AB.
Putting x = 0, y = 0 in (1), 0 + 0 150 i.e. 0 150, which
is true.
Origin lies in the region.
(2)′ passes thro’ C (80, 0) and D (0, 20).
(2)′ represents the line CD.
Putting x = 0, y = 0 in (2), 0 + 0 80 i.e. 0 80, which is
true.
Origin lies in the region.
Now x 15 represents the line x = 15 and left of it.
And y 0 represents x-axis and above it.
The common region is shown as shaded in the figure.
Question 77:
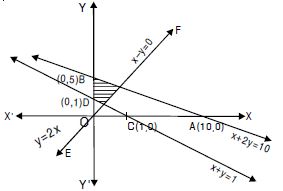
Solve the following system of inequalities graphically :
x + 2y 10, x + y 1, x – y 0 x 0, y 0.
Answer:
The given inequalities are
x + 2y 10 ....(1)
x + y 1 ....(2)
x – y 0 ....(3)
x 0, y 0 ....(4)
The corresponding equations are
x + 2y = 10 ....(1)′
x + y = 1 ....(2)′
x – y = 0 ....(3)′
and x = 0, y = 0 ....(4)′
(1)′ passes thro’ A (10, 0) and B (0, 5)
(1)′ represents the line AB.
Putting x = 0, y = 0, 0 + 0 10 i.e. 0 10, which is true.
Origin lies in the region.
(2)′ passes thro’ C (1, 0) and D (0, 1)
(2)′ represents the line CD.
Putting x = 0, y = 0, 0 + 0 1 i.e. 0 1, which is nottrue.
Origin does not lie in the region.
(3)′ i.e. x – y = 0 passes thro’ (0, 0) and (1, 1).
(3)′ represents the line EF.
Putting x = 0, y = 1, 0 – 1 0, i.e. – 1 0 which is true.
(0, 1) lies in the region.
And x 0, y 0 represents Ist-quadrant.
The common region is shown as shaded in the figure.