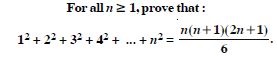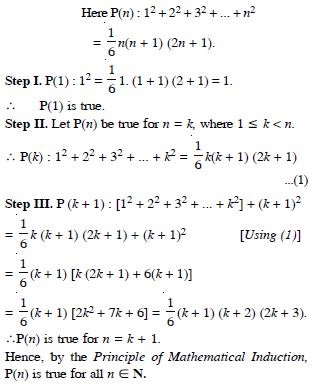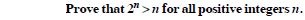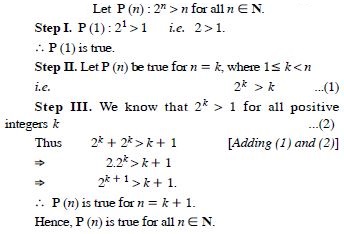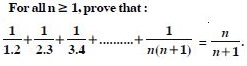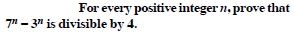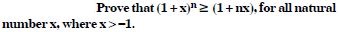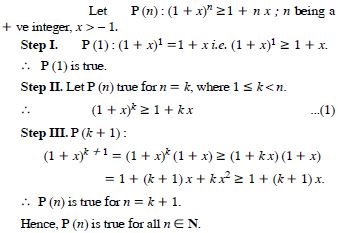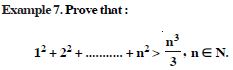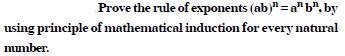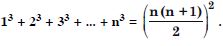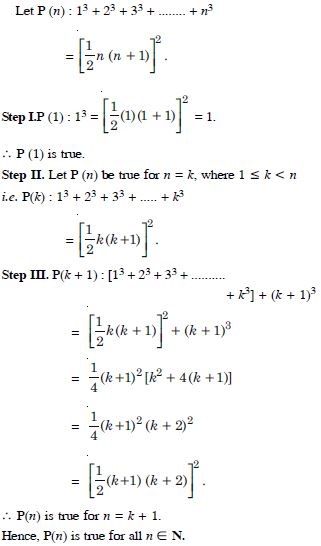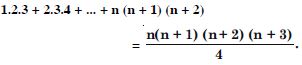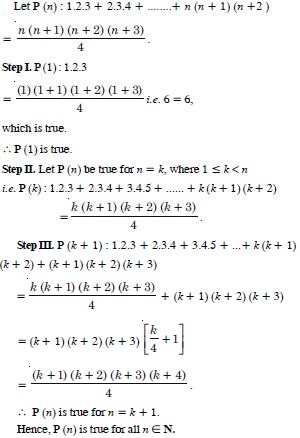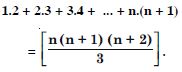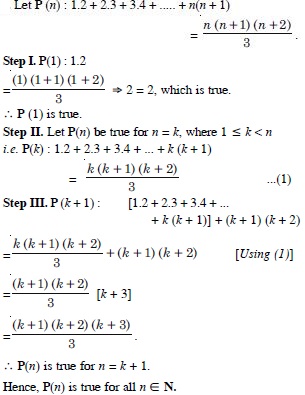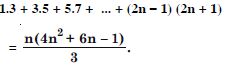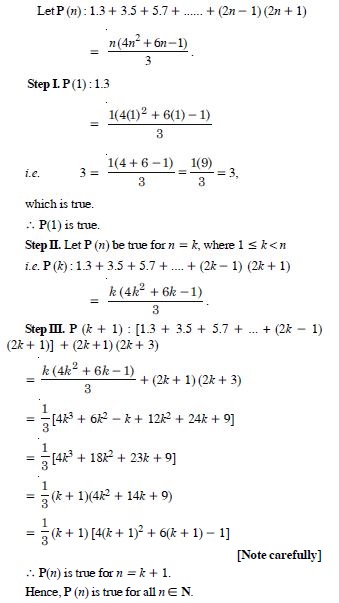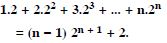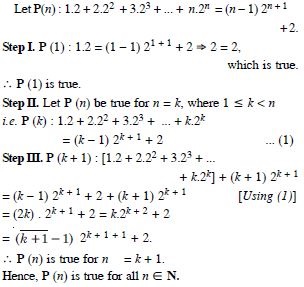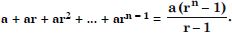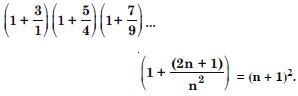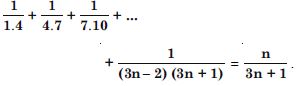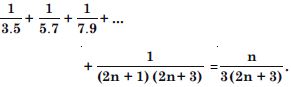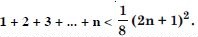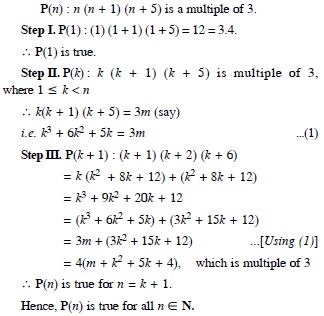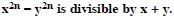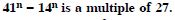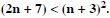NCERT Solutions for Class 11 Mathematical Induction | Aasoka

Practice your Maths skills with Free NCERT Solutions at Aasoka. Prepared by the subject matter experts, these solutions help students score the marks they desire. Students can also prepare for competitive exams such as JEE and NEET with the help of NCERT Solutions for Class 11. These solutions come in handy when students want to enhance their skills. The questions and answers are as per the latest CBSE syllabus which makes it easier for students to cover the entire chapter.

The “Mathematical Induction” chapter of Maths Class 11 covers problems and applications related to the principle of mathematical induction, the process of providing induction, deduction, and much more.

Question 1:

Answer:

Show Answer

Question 2:

Answer:

Show Answer

Question 3:

Answer:

Show Answer

Question 4:

Answer:

Show Answer

Question 5:

Answer:

Show Answer

Question 6:

Answer:

Show Answer

Question 7:

Answer:

Show Answer

Question 8:

Answer:

Show Answer

Question 9:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 10:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 11:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 12:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 13:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 14:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question :15

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 16:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 17:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 18:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 19:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 20:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 21:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 22:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 23:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 24:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 25:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 26:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 27:

n (n + 1) (n + 5) is a multiple of 3.

Answer:

Show Answer

Question 28:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 29:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 30:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 31:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer

Question 32:

Prove the following by using principle of mathematical induction for all n $\in$ N :

Answer:

Show Answer