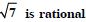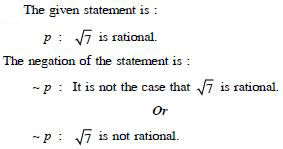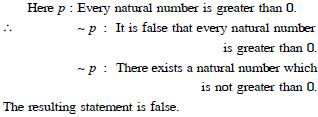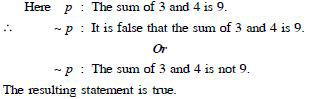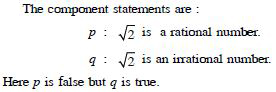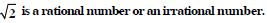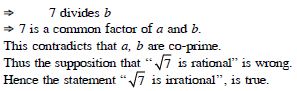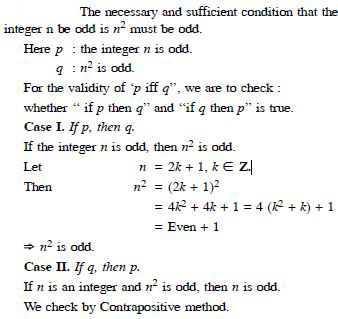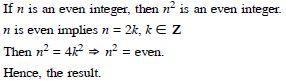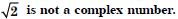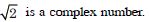Free NCERT Solutions are available on Aasoka for the students to boost their performance for the exams. These solutions come in handy whenever students want to learn, study, and understand the concepts. Designed by the subject matter experts, the questions and answers in the NCERT Solutions for Class 11 are as per the latest CBSE syllabus. So, grab top-quality educational resources at Aasoka and score excellent marks in your exams.
In the chapter “Mathematical Reasoning” of Maths Class 11, students will learn compound statements, connecting words/phrases, mathematically acceptable statements, contrapositive and converse, validating the statements involving the connecting words, quantifiers, implications, negation, the negation of statements, and much more.
Question 1:
Check whether the following sentences are statements. Give reasons for your answer.
8 is less than 6
Answer:
The given sentence is false.
[8 is greater than 6]
Hence, it is a statement.
Question 2:
Check whether the following sentences are statements. Give reasons for your answer.
Every set is a finite set
Answer:
The given sentence is false.
[There are sets, which are not finite]
Hence, it is a statement.
Question 3:
Check whether the following sentences are statements. Give reasons for your answer.
The sun is a star
Answer:
The given sentence is true.
[It is scientifically established fact ]
Hence, it is a statement.
Question 4:
Check whether the following sentences are statements. Give reasons for your answer.
Mathematics is fun
Answer:
The given sentence is not always true.
[It may be fun for those who like Mathematics
but it is not fun for others]
Hence, it is not a statement.
Question 5:
Check whether the following sentences are statements. Give reasons for your answer.
There is no rain without clouds
Answer:
This sentence is true.
[It is scientifically established natural phenomenon]
Hence, it is a statement.
Question 6:
Check whether the following sentences are statements. Give reasons for your answer.
How far is chennai from here ?
Answer:
This is not a statement.
[The sentence contains the word “here”]
Question 7:
Write the negation of the following statements :
Both the diagonals of a rectangle have the same
length
Answer:
The given statement is :
p : Both the diagonals of a rectangle have same length.
The negation of the statment is :
~ p : It is false that both the diagonals of a rectangle have
the same length.
Or
~ p : There is atleast one rectangle whose both diagonals
do not have the same length.
Question 8:
Write the negation of the following statements :
Answer:
Question 9:
Write the negation of the following statements and check whether the resulting statements
are
true :
Australia is a continent.
Answer:
Question 10:
Write the negation of the following statements and check whether the resulting statements
are
true :
There does not exist a quadrilateral which has all
its sides equal.
Answer:
Question 11:
Write the negation of the following statements and check whether the resulting statements
are
true :
Every natural number is greater than 0.
Answer:
Question 12:
Write the negation of the following statements and check whether the resulting statements
are
true :
The sum of 3 and 4 is 9.
Answer:
Question 13:
Find the component statements of the following compound statements :
The sky is blue and the grass is green
Write the connecting word in each case.
Answer:
The component statements are :
p : The sky is blue.
q : The green is green.
The connecting word is ‘and’.
Question 14:
Find the component statements of the following compound statements :
It is raining and it is cold.
Write the connecting word in each case.
Answer:
The component statements are :
p : It is raining.
q : It is cold.
The connecting word is ‘and’.
Question 15:
Find the component statements of the following compound statements :
All rational numbers are real and all real numbers are complex.
Write the connecting word in each case.
Answer:
The component statements are :
p : All rational numbers are real.
q : All real numbers are complex.
The connecting word is ‘and’.
Question 16:
Find the component statements of the following compound statements :
0 is a positive number or a negative number.
Write the connecting word in each case.
Answer:
The component statements are :
p : 0 is a positive number.
q : 0 is a negative number.
The connecting word is ‘or’.
Question 17:
Find the component statements of the
following and check whether they are true or not :
A square is a quadrilateral and its four sides
are equal.
Answer:
The component statements are :
p : A square is a quadrilateral.
q : A square has all its four sides equal.
Here p and q are both true.
Question 18:
Find the component statements of the
following and check whether they are true or not :
All prime numbers are either even or odd.
Answer:
The component statements are :
p : All prime numbers are even.
q : All prime numbers are odd.
Here p and q are both false.
Question 19:
Find the component statements of the
following and check whether they are true or not :
A person who has taken Mathematics or
Computer Science can go for MCA.
Answer:
The component statements are :
p : A person who has taken
Mathematics can go for MCA.
q : A person who has taken Computer
Science can go for MCA.
Here p and q are both true.
Question 20:
Find the component statements of the
following and check whether they are true or not :
Chandigarh is the capital of Haryana and U.P.
Answer:
The component statements are :
p : Chandigarh is the capital of
Haryana.
q : Chandigarh is the capital of U.P.
Here p is true but q is false.
Question 21:
Find the component statements of the following and check whether they are true or not :
Answer:
Question 22:
Find the component statements of the
following and check whether they are true or not :
24 is a multiple of 2, 4 and 8.
Answer:
The component statements are :
p : 24 is a multiple of 2.
q : 24 is a multiple of 4.
r : 24 is a multiple of 8.
Here p, q, r are all true.
Question 23:
Write the component statements of
the following compound statements and check
whether the compound statement is true or false.
A line is straight and extends indefinitely in
both directions.
Answer:
The component statements are :
p : A line is straight.
q : A line extends indefinitely in both directions.
Since p and q are both true,
the compound statement (p q) is true.
Question 24:
Write the component statements of
the following compound statements and check
whether the compound statement is true or false.
0 is less than every positive integer and every
negative integer.
Answer:
The component statements are :
p : 0 is less than every positive integer.
q : 0 is less than every negative integer.
Since p is true and q is false,
the compound statement (p q) is false.
Question 25:
Write the component statements of
the following compound statements and check
whether the compound statement is true or false.
All living things have two legs and two eyes.
Answer:
The component statements are :
p : All living things have two legs.
q : All living things have two eyes.
Since p and q are both false,
the compound statement (p q) is false.
Question 26:
For each of the following statements,
determine whether an inclusive ‘Or’ or exclusive ‘Or’ is
used. Give reasons for your answer.
To enter a country, you need a passport or a
voter registration card.
Answer:
p : To enter a country, you need a passport.
q : To enter a country, you need a voter
registration card.
To enter a country, you need either a passport or a voter
registration card as well as you have both.
Thus ‘Or’ is inclusive.
Question 27:
For each of the following statements,
determine whether an inclusive ‘Or’ or exclusive ‘Or’ is
used. Give reasons for your answer.
The school is closed if it is a holiday or a Sunday.
Answer:
p : The school is closed if it is a holiday.
q : The school is closed if it is a Sunday.
The school is closed if it is either a holiday or it is Sunday
as well as it is both.
Thus ‘Or’ is inclusive.
Question 28:
For each of the following statements,
determine whether an inclusive ‘Or’ or exclusive ‘Or’ is
used. Give reasons for your answer.
Two lines intersect at a point or are paralel.
Answer:
p : Two lines intersect at a point.
q : Two lines are parallel.
Since two lines cannot intersect at a point as well as they
are parallel,
‘Or’ is exclusive.
Question 29:
For each of the following statements,
determine whether an inclusive ‘Or’ or exclusive ‘Or’ is
used. Give reasons for your answer.
Students can take French or Sanskrit as their
third language.
Answer:
p : Students can take French as their third language.
q : Students can take Sanskrit as their third
language.
Since students cannot take both French and Sanskrit as
their third language,
‘Or’ is exclusive.
Question 30:
Identify the type of ‘Or’ used in the following statements and check whether the statements are true or false.
Answer:
Question 31:
Identify the type of ‘Or’ used in the following statements and check whether the
statements
are true or false.
To enter into public library children need an
identity card from the school or a letter from the
school authorities.
Answer:
p : To get into a public library children need an
identity card.
q : To get into a public library children need letter
from the school authorities.
Children can enter the library if they have either identity
card or the letter as well as when they have both.
Thus ‘Or’ is inclusive.
The compound statement is also true when children
have both card and the letter.
Question 32:
Identify the type of ‘Or’ used in the following statements and check whether the
statements
are true or false.
A rectangle is a quadrilateral or a 5-sided
polygon.
Answer:
p : A rectangle is a quadrilateral.
q : A rectangle is a 5-sided polygon.
Since p is true and q is false and ‘Or’ is exclusive,
the compound statement is true.
Question 33:
Write the contrapositive of the following statements :
If a number is divisible by 9, then it is divisible by 3.Answer:
We have :
antecedent : p : A number is divisible by 9.
consequent : q : The number is divisible by 3.
~ p : A number is not divisible by 9.
~ q : The number is not divisible by 3.
The contrapositive of the statement p q is
~ q ~ p.
Its statement is :
If a number is not divisible by 3, it is not divisible by 9.
Question 34:
Write the contrapositive of the following statements :
If you are born in India, then you are a citizen of
India.
Answer:
We have :
antecedent : p : You are born in India.
consequent : q : You are a citizen of India.
~ p : You are not born in India.
~ q : You are not a citizen of India.
The contrapositive of the statement p q is ~ q ~ p.
Its statement is :
If you are not a citizen of India, then you are not born in
India.
Question 35:
Write the contrapositive of the following statements :
If a triangle is equilateral, it is isosceles.
Answer:
We have :
antecedent : p : Triangle is equilateral.
consequent : q : Triangle is isosceles.
~ p : Triangle is not equilateral
~ q : Triangle is not isosceles.
The contrapositive of the statement p q is ~ q ~ p.
Its statement is :
If a triangle is not isosceles, then it is not equilateral.
Question 36:
Write the converse of the following statements :
If a number n is even, then n2 is even.
Answer:
The converse of the given statements are :
If a number n2 is even, then n is even.
Question 37:
Write the converse of the following statements :
If you do all the exercises in the book, you get an
A grade in the class.
Answer:
The converse of the given statements are :
If you get an A-grade in the class, then you have done
all the exercises of the book.
Question 38:
Write the converse of the following statements :
If two integers a and b are such that a > b, then
a – b is always a positive integer.
Answer:
The converse of the given statements are :
If two integers a and b are such that a – b is always a
positive integer, then a > b.
Question 39:
For each of the following compound
statements, first identify the corresponding component
statements. Then check whether the statements are true
or not :
If a triangle ABC is equilateral, then it is isosceles.
Answer:
The statement is of the from ‘if p, then q’.
(i) p : Triangle is equilateral
q : Triangle is isosceles.
Here p Triangle is equilateral
Triangle is isosceles [Equilateral triangle is isosceles]
q.
Hence, the compound statement is true.
Question 40:
For each of the following compound
statements, first identify the corresponding component
statements. Then check whether the statements are true
or not :
If a, b are integers, then ab is a rational number.
Answer:
p : a, b are integers
q : ab is a rational number
p a, b are integers
(ab) is an integer
[Product of two integers is an integer]
ab is a rational number.
[Integer is a rational number]
q.
Hence, the compound statement is true.
Question 41:
Given below are two pairs of
statements. Combine these two statements using
if and only if :
p : If a rectangle is a square, then all its four
sides are equal.
q : If all the four sides of a rectangle are equal,
then the rectangle is a square.
Answer:
A rectangle is a square if and only if all its four sides are equal.
Question 42:
Given below are two pairs of
statements. Combine these two statements using
if and only if :
p : If the sum of digits of a number is divisible
by 3, then the number is divisible by 3.
q : If a number is divisible by 3, then the sum of
its digits is divisible by 3.
Answer:
A number is divisible by 3 if and only if the sum of its digits is divisible by 3.
Question 43:
Check whether the following statement is true or not. If x, y Z are such that x and y are odd, then xy is odd.
Answer:
Let p : x, y Z such that x and y are odd
q : xy is odd.
(a) We can apply Rule–3, Case I (‘if – then’) :
i.e.if ‘p’ is true, then ‘q’ is true.
‘p’ is true x and y are odd integers.
Then x = 2l + 1 for l Z
and y = 2m + 1 for m Z.
Then xy = (2l + 1) (2m + 1)
= 2 (2lm + l + m) + 1
xy is odd.
Hence the given statement is true.
(b) We can also apply Rule–3, Case II (‘if – then) :
i.e.if ‘q’ is not true, then ‘p’ is not true.
Assume that ‘q’ is not true.
~ q : xy is true.
This is possible only if either x or y is even
p is not true.
Thus q p.
Hence the result.
Question 44:
Check whether the following statement is
true or false by its contrapositive :
“If x, y Z, such that xy is odd,
then both x and y are odd.”
Answer:
p : xy is odd
q : Both x and y are odd.
Here we check whether the statement p q is true or not
by checking its contrapositive
i.e. q p.
Now q : It is false that both x and y are odd :
x (or y) is even.
Let x = 2n for some n Z
xy = 2ny for some n Z
xy is even
p is true.
Thus q p.
Hence, the given statement is true.
Question 45:
Answer:
Question 46:
By giving a counter example, show that
the following statement is false.
‘‘If n is an odd integer, then n is prime.’’
Answer:
The given statement is of the type :
‘‘If p then q’’.
To show that this is false.
For this we need to show that ‘‘if p then ~ q”.
Take an odd integer, which is not prime.
Let n = 9.
With this, the given statement is false.
Question 47:
Check whether ‘‘or’’ used in the following
compound statement is exclusive or inclusive ? Write the
component statements of the compound statement and use
them to check whether the compound statement is true or
not. Justify your answer.
t : you are wet when it rains
Or
you are in a river.
Answer:
‘‘Or’’ used in the given statement is inclusive.
[ It is possible that it rains and you are in the river]
The component statements of the given compound
statement are :
p : You are wet when it rains.
q : You are wet when you are in a river.
Since ‘p’ and ‘q’ are both true,
(p ∨ q), the compound statement, is also true.
Question 48:
Write the negation of the following statements :
p : For every real number x, x2 > x.
Answer:
p : There exists a real number x such that x2 < x.
Question 49:
Write the negation of the following statements :
q : There exists a rational number x such that
x2 = 2.
Answer:
q : There does not exist a rational number x such that x2 = 2.
Question 50:
Write the negation of the following statements :
r : All birds have wings.
Answer:
r : There exists a bird which has no wings.
Question 51:
Write the negation of the following statements :
s : All students study Mathematics at the
elementary level.
Answer:
Question 52:
For the given statements identify the
necessary and sufficient conditions.
t : If you drive over 80 km per hour, then you will get
a fine.
Answer:
Let the statements be :
p : You drive over 80 km per hour
q : You will get a fine.
Now ‘if p, then q’ indicates that p is sufficient for q
i.e. driving over 80 km per hour is sufficient to get a fine.
Hence the sufficient condition is :
“driving over 80 km per hour’’
Again ‘if p, then q’ indicates that q is necessary for p
i.e. when you drive over 80 km per hour, you will
necessarily get a fine.
Hence, the necessary condition is :
“getting a fine”.
Question 53:
Which of the following sentences are statements ?
Give reasons for your answer.
There are 35 days in a month.
Answer:
Statement.
This is false.
[ A month cannot have 35 days]
Question 54:
Which of the following sentences are statements ?
Give reasons for your answer.
Mathematics is difficult.
Answer:
Not a statement.
Mathematics may be difficult to one but easy to the other.
Question 55:
Which of the following sentences are statements ?
Give reasons for your answer.
The sum of 5 and 7 is greater than 10.
Answer:
Statement.
This is true. [ 5 + 7 = 12 > 10]
Question 56:
Which of the following sentences are statements ?
Give reasons for your answer.
The square of a number is an even number.
Answer:
Not a statement.
The sentence is sometimes true and sometimes false.
For Ex. 22 = 4, which is even and
32 = 9, which is odd.
Question 57:
Which of the following sentences are statements ?
Give reasons for your answer.
The sides of a quadrilateral have equal length.
Answer:
Statement.
The sentence is sometimes true and sometimes false.
For Ex. Square and Rhombus have equal length whereas
rectangle and trapezium have unequal lengths.
Question 58:
Which of the following sentences are statements ?
Give reasons for your answer.
Answer this question.
Answer:
Not a statement.
In fact it is an order.
Question 59:
Which of the following sentences are statements ?
Give reasons for your answer.
The product of (– 1) and 8 is 8.
Answer:
Statement.
This is false. [ (– 1) (8) = – 8]
Question 60:
Which of the following sentences are statements ?
Give reasons for your answer.
The sum of all interior angles of a triangle
is 180.
Answer:
Statement.
This is always true.
Question 61:
Which of the following sentences are statements ?
Give reasons for your answer.
Today is a windy day.
Answer:
Not a statement.
From the context, it is not clear which day is referred.
Question 62:
Which of the following sentences are statements ?
Give reasons for your answer.
All real numbers are complex numbers.
Answer:
Statement.
This is true.
[ Each real number ‘a’ can be written as a + i0]
Question 63:
Give three examples of sentences, which are not statements. Give reasons for the answers.
Answer:
The three examples are :
(i) It is a windy day.
Which day is a windy day ? We cannot say which day is
windy.
(ii) She is very beautiful.
Who is beautiful ?
Question 64:
Write the negation of the following statements :
Chennai is the capital of Tamil Nadu.
Answer:
Negation of the given statements are as given below :
Chennai is not the capital of Tamil Nadu.
Question 65:
Write the negation of the following statements :
Answer:
Negation of the given statements are as given below :
Question 66:
Write the negation of the following statements :
All triangles are not equilateral triangles.
Answer:
Negation of the given statements are as given below :
All triangles are equilateral triangles.
Question 67:
Write the negation of the following statements :
The number 2 is greater than 7.
Answer:
Negation of the given statements are as given below :
The number 2 is not greater than 7.
Question 68:
Write the negation of the following statements :
Every natural number is an integer.
Answer:
Negation of the given statements are as given below :
Every natural number is not an integer.
Question 69:
Are the following pairs of statements negation of
each other ?
The number x is not a rational number.
The number x is not an irrational number.
Answer:
The negative of the statement
“The number x is not a rational number”
~ The number x is a rational number.
The number x is not an irrational number.
Hence the statements are negation of each other.
Question 70:
Are the following pairs of statements negation of
each other ?
The number x is a rational number.
The number x is an irrational number.
Answer:
The negation of the statement
“The number is a rational number”
~ The number x is not a rational number.
x is an irrational number.
The statements are not nagation of each other.
Question 71:
Find the component statements of the following
compound statements and check whether they are true or
false.
Number 3 is prime or it is odd.
Answer:
The component statements are :
p : Number 3 is prime.
q : Number 3 is odd.
Here p and q are both true.
The compound statement is true.
Question 72:
Find the component statements of the following
compound statements and check whether they are true or
false.
All integers are positive or negative.
Answer:
The component statements are :
p : All integers are positive.
q : All integers are negative.
Here p and q are both false.
The compound statement is false.
Question 73:
Find the component statements of the following
compound statements and check whether they are true or
false.
100 is divisible by 3, 11 and 5.
Answer:
The component statements are :
p : 100 is divisible by 3.
q : 100 is divisible by 11.
and r : 100 is divisble by 5.
Here p, q are false and r is true.
The compound statement is false.
Question 74:
For each of the following compound statements first
identify the connecting words and then break it into
component statements :
All rational numbers are real and all real numbers
are not complex.
Answer:
Connecting word is “And”.
The component statements are :
All rational numbers are real.
All real numbers are not complex.
Question 75:
For each of the following compound statements first
identify the connecting words and then break it into
component statements :
Square of an integer is positive or negative.
Answer:
Connecting word is “Or”.
The component statements are :
Square of an integer is positive.
Square of an integer is negative.
Question 76:
For each of the following compound statements first
identify the connecting words and then break it into
component statements :
The sand heats up quickly in the sun and does not
cool down fast at night.
Answer:
Connecting word is “And”. The component statements are : The sand heats up quickly in the sun. The sand does not cool down fast at night.
Question 77:
For each of the following compound statements first
identify the connecting words and then break it into
component statements :
x = 2 and x = 3 are the roots of the equation
3x2 – x – 10 = 0.
Answer:
Connecting word is “And”.
The component statements are :
x = 2 is root of the equation 3x2 – x – 10 = 0.
x = 3 is root of the equation 3x2 – x – 10 = 0.
Question 78:
Identify the quantifier in the following statements and
write the negation of the statements.
There exists a number, which is equal to its square.
Answer:
The given statement contains existential quantifier
‘there exists’.
Now the statement is :
p : A number is equal to its square.
The negation of the statement is obtained by replacing
existential quantifier by a universal quantifier and then
negate p.
The negation of given statement is :
For all numbers they are not equal to their square.
Question 79:
Identify the quantifier in the following statements and
write the negation of the statements.
For every real number x, x is less than x + 1.
Answer:
The given statement contains universal quantifier ‘for
every’.
Now the statement is :
p : x is less than x + 1.
The negation of the statement is obtained by replacing
universal quantifier by a existential quantifier and then
negate p.
The negation of given statement is :
“For some real number, x is not less than x + 1”.
Question 80:
Identify the quantifier in the following statements and
write the negation of the statements.
There exists a capital for every state in India.
Answer:
The given statement contains existential quantifier
‘there exists’.
Now the statement is :
p : A capital for every state in India.
The negation of the statement is obtained by replacing
existential quantifier by a universal quantifier and then
negate p.
The negation of given statement is :
“There exists a state in India which does not have capital.”
Question 81:
Check whether the following pairs of statements are
negation of each other. Give reasons for your answer :
(i) x + y = y + x is true for every real numbers x
and y.
(ii) There exists real numbers x and y for which
x + y = y + x.
Answer:
No.
Negation of statement is :
“There exist real numbers x and y for which
x + y ≠ y + x”.
Question 82:
State whether, “or” used in the following
statements is exclusive or inclusive. Give
reasons for your answer :
Sun rises or Moon sets.
Answer:
Here “Or” is exclusive.
[ Sun rises and moon sets during day time]
Question 83:
State whether, “or” used in the following
statements is exclusive or inclusive. Give
reasons for your answer :
To apply for a driving licence, you should
have a ration card or a passport.
Answer:
Here “Or” is inclusive.
[ A person can have both a ration card and a
passport to apply for a driving licence]
Question 84:
State whether, “or” used in the following
statements is exclusive or inclusive. Give
reasons for your answer :
All integers are positive or negative.
Answer:
Here “Or” is exclusive.
[ All integers cannot be both positive as well as
negative]
Question 85:
Rewrite the following statement with ‘if-then’ in five different ways conveying the same meaning. If a natural number is odd, then its square is also odd.
Answer:
The given statement can be rewritten in the
following five different ways conveying the same meaning :
(i) A natural number is odd implies that its square is
odd.
(ii) A natural number is odd only if its square is odd.
(iii) For a natural number to be odd, it is necessary that
its square is odd.
(iv) For the square of a natural number to be odd, it is
sufficient that the number is odd.
(v) If the square of a natural number is not odd, then
the natural number is not odd.
Question 86:
Write the contrapositive and converse of the
following statements :
If x is a prime number, then x is odd.
Answer:
Contrapositive :
If a number x is not odd, then x is not a prime number.
Converse :
If a number is odd, then it a prime number.
Question 87:
Write the contrapositive and converse of the
following statements :
If two lines are parallel, then they do not
intersect in the same plane.
Answer:
Contrapositive :
If two lines intersect in the same plane, then they are not
parallel.
Converse :
If the two lines do not intersect in the same plane, then
they are parallel.
Question 88:
Write the contrapositive and converse of the
following statements :
Something is cold implies that it has low
temperature.
Answer:
Contrapositive :
If something is not at low temperature, then it is not cold.
Converse :
If something is at low temperature, then it is cold.
Question 89:
Write the contrapositive and converse of the
following statements :
You cannot comprehend geometry if you do not
know how to reason deductively.
Answer:
Contrapositive :
If you know how to reason deductively, then you cannot
comprehend and geometry.
Converse :
If you do not know how to reason deductively, then you
cannot comprehend geometry.
Question 90:
Write the contrapositive and converse of the
following statements :
x is even number implies that x is divisible by 4.
Answer:
Contrapositive :
If x is not divisible by 4, then x is not an even number.
Converse :
If x is divisible by 4, then x is an even number.
Question 91:
Write each of the following statements in the form ‘if then’ :
You get a job implies that your credentials are
good.
Answer:
If you get a job, then your credentials are good.
Question 92:
Write each of the following statements in the form ‘if then’ :
The Banana tree will bloom if it stays warm for
a month.
Answer:
If it stays for a month, then Banana tree will bloom.
Question 93:
Write each of the following statements in the form ‘if then’ :
A number is even if it is a multiple of 2.
Answer:
If a number is even, then it is a multiple of 2.
Question 94:
Write each of the following statements in the form ‘if then’ :
A quarilateral is a parallelogram if its diagonals
bisect each other.
Answer:
If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
Question 95:
Given statements in (a) and (b). Identify the statements
given below as contrapositive or converse of each other.
(i) If you live in Delhi, then you have winter clothes.
(ii) If you have winter clothes, then you live in
Delhi.
Answer:
The component statements are :
p : You live in Delhi.
q : You have winter clothes.
The given statements are of the type :
(i) p q
(ii) q p
(iii) q p.
Clearly (i) and (ii) are contrapositive of each other
and (i) and (iii) are converse of each other.
Question 96:
Given statements in (a) and (b). Identify the statements
given below as contrapositive or converse of each other.
(i) If a quadrilateral is a paralleogram, then its
diagonals bisect each other.
(ii) If the diagonals of a quadrilateral do not bisect
each other, then the quadrilateral is not a
parallelogram.
(iii) If the diagonals of a quadrilateral bisect each
other, then it is a parallelogram.
Answer:
The component statements are :
p : Quadrilateral is a parallelogram.
q : Diagonals bisect each other.
The given statements are of the type :
(i) p q
(ii) q p
(iii) q p.
Clearly (i) and (ii) one contrapositive of each other.
and (i) and (iii) are converse of each other.
Question 97:
Show that the statement :
p : “If x is a real number such that x3 + 4x = 0, then x is 0” is true by
:
direct method
Answer:
Let q : x is a real number such that x3 + 4x = 0 r : x is 0.
Then p : If q, then r.
Direct Method.
Let q be true.
Then x is a real number such that x3 + 4x = 0
x is a real number such that x (x2 + 4) = 0
x = 0 [ x2 + 4 ≠ 0 for x R]
r is true.
Thus q is true r is true.
Hence p is true.
Question 98:
Show that the statement :
p : “If x is a real number such that x3 + 4x = 0, then x is 0” is true by
:
method of contradiction
Answer:
Let q : x is a real number such that x3 + 4x = 0 r : x is 0.
Then p : If q, then r.
Method of Contradiction.
Let us assume that ‘p’ is not true.
Then p is true
(q r) is true
q and r are true [ (q r) ≡ q and r]
x is a real number such that x3 + 4x = 0 and x ≠ 0
x = 0 and x ≠ 0.
This leads to contradiction.
Hence p is true.
Question 99:
Show that the statement : p : “If x is a real number such that x3 + 4x = 0, then x is 0” is true by : method of contrapositive
Answer:
Let q : x is a real number such that x3 + 4x = 0 r : x is 0.
Then p : If q, then r.
Method of Contrapositive.
Let r be not true.
Then x ≠ 0; x R
x3 + 4x ≠ 0; x R
q is not true
q is true
Thus r q.
Hence p : q r is true.
Question 100:
Show that the statement :
“For any real numbers a and b, a2 = b2 implies that
a = b”
is not true by giving a counter example.
Answer:
Counter Example :
Table a = 5 and b = – 5.
Here a2 = b2 [ each = 25]
but a ≠ b.
Question 101:
Show that the following statement is true by the
method of contrapositive.
p : if x is an integer and x2 is even, then x is also
even.
Answer:
Let the statements be :
q : If x is an integer and x2 is even
r : x is even.
Thus p : “If q, then r”.
Let us suppose that r is false.
Then x is not an even integer
x is an odd integer
x = 2m + 1 for some m Z
x2 = 4m2 + 4m + 1
x2 = 4m (m + 1) + 1
x2 is an odd integer
q is false.
Thus r is false
q is false.
Hence p : “If q, then r” is true.
Question 102:
By giving a counter example, show that the following
statements are not true :
p: If the angles of a triangle are equal, then the
triangle is an obtuse angled triangle.
Answer:
The given statement is in the form ‘if p
then q’. To show that this is false, we are to show that if ‘p’
then q’.
We take a triangle whose all angles are less than 90.
Let each angle be 65.
Then sum of angles = 3 × 65 = 195 > 180.
Thus p is true
q is false.
Hence the given statement is not true.
Question 103:
By giving a counter example, show that the following
statements are not true :
q : The equation x2 – 1 = 0 does not have a root
lying between 0 and 2.
Answer:
Counter Example : The equation x2 – 1 = 0 has a root – 1, which does not lie between 0 and 2.
Question 104:
Which of the following statements are true and which are false ? In each case give a
valid
reason for saying so.
p : Each radius of a circle is a chord of the circle.
Answer:
False.
By definition, the chord intersects the circle in two parts.
Question 105:
Which of the following statements are true and which are false ? In each case give a
valid
reason for saying so.
q : The centre of a circle bisects each chord of
the circle.
Answer:
False.
Counter Example. A chord, which is not a diameter.
Question 106:
Which of the following statements are true and which are false ? In each case give a
valid
reason for saying so.
r : Circle is a particular case of an ellipse.
Answer:
Question 107:
Which of the following statements are true and which are false ? In each case give a
valid
reason for saying so.
s : If x and y are integers such that x > y, then –
x < – y.
Answer:
True.
By Rule of Inequality, x > y
– x < – y.
Question 108:
Which of the following statements are true and which are false ? In each case give a valid reason for saying so.