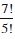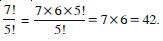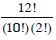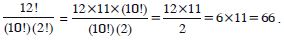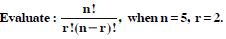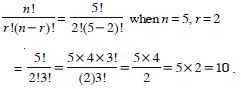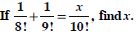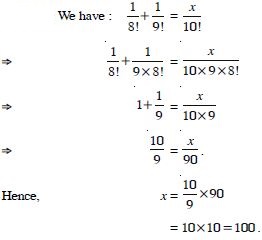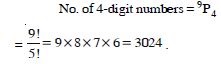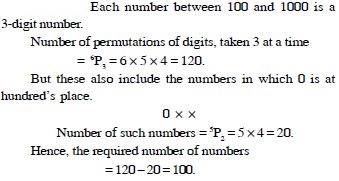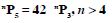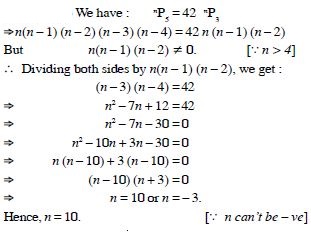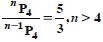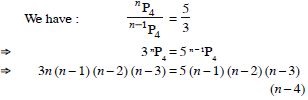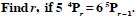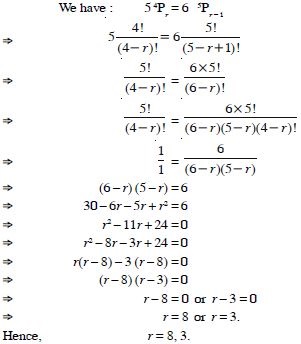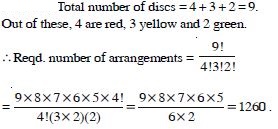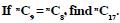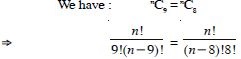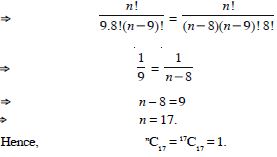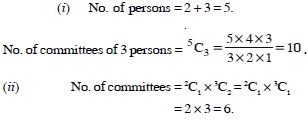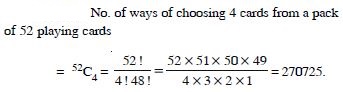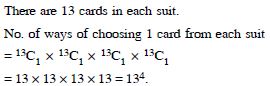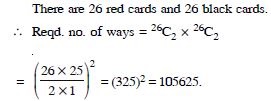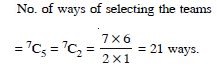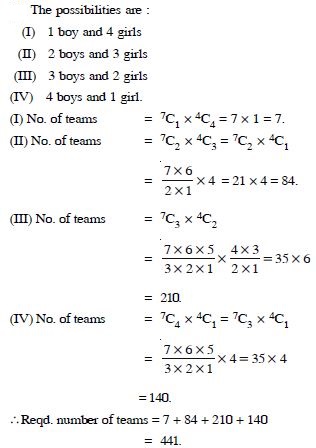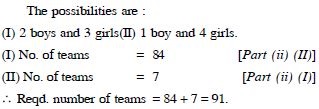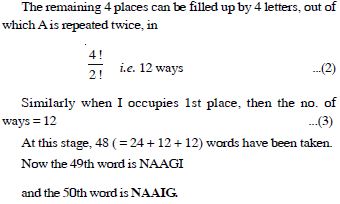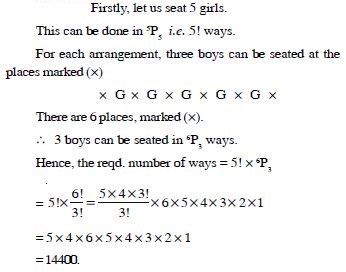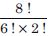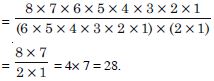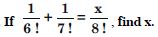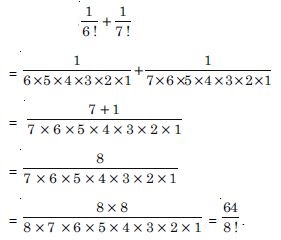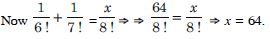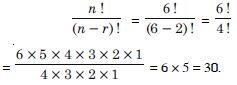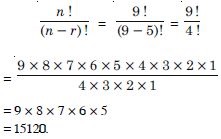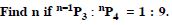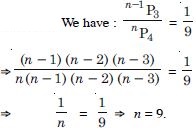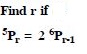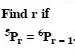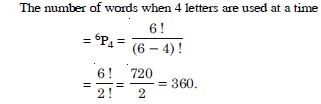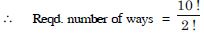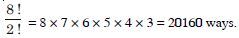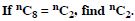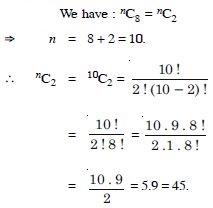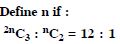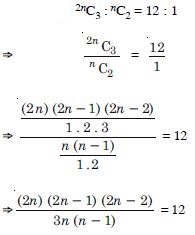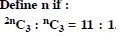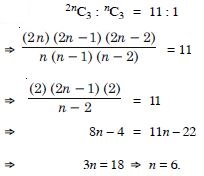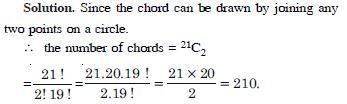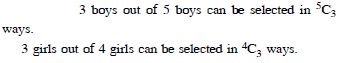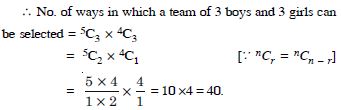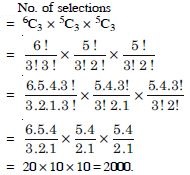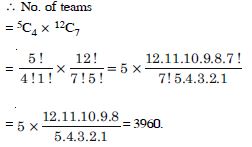Aasoka offers free NCERT Solutions for Class 11 students to kick-start their exam preparation for school as well as competitive exams. We provide top educational resources designed in accordance with the latest CBSE syllabus and guidelines. The NCERT Solutions makes it easier for students to study, learn, and understand the topics of the chapter “Permutations and Combinations”.
The chapter “Permutations and Combinations” of Class 11 Maths explains topics such as formulae and their connections, the fundamental principle of counting, simple applications, permutations and combinations, factorial n, etc.
Question 1:
Find the number of 4 letter words, with or without meaning, which can be formed out of the letters of the word ROSE, where the repetition of the letters is not allowed.
Answer:
There are as many words as there are ways of
filling 4 vacant places by 4 letters, where the repetition of
letters is not allowed.
First place can be filled in 4 different ways by any one of
the four letters R, O, S, E.
Second place can be filled in 3 different ways by any one
of the remaining 3 letters.
Similarly 3rd and fourth places can be filled up in 2 and 1
way respectively.
By FPC, the number of ways in which 4 places can be
filled = 4 × 3 × 2 × 1 = 24.
Hence, the required number of words = 24.
Question 2:
Given 4 flags of different colours, how many different signals can be generated, if a signal requires the use of 2 flags one below the other ?
Answer:
First flag can be selected in 4 different ways. Second flag can be selected in 3 different ways. By FPC, the required number of signals = 4 × 3 = 12.
Question 3:
How many 2-digit even numbers can be formed from the digits 1, 2, 3, 4 and 5, if the digits can be repeated ?
Answer:
There are five given digits viz. 1, 2, 3, 4 and 5.
To form 2-digit even numbers, we are to fill up the unit’s
place either by 2 or by 4.
The unit’s place can be filled up in 2 different ways.
The ten’s place can be filled up in 5 different ways
because any one can fill up this place.
By PFC, the total no. of 2-digit even numbers
= 2 × 5 = 10.
Question 4:
Find the number of different signals that can be generated by arranging at least 2 flags in order (one below the other) on a vertical staff, if five flags are available.
Answer:
A signal consists of either 2 flags, 3 flags,
4 flags or 5 flags.
2 Flag-Signals
There are 5 flags.
First place can be filled in 5 ways.
Second place can be filled in 4 ways.
By FPQ, the two places can be filled up in 5 × 4 = 20
ways.
Thus the no. of 2 flag signals = 20.
Similarly, the no. of 3 flag signals = 5 × 4 × 3 = 60,
the no. of 4 flag signals = 5 × 4 × 3 × 2
= 120
and the no. of 5 flag signals = 5 × 4 × 3 × 2 × 1
= 120.
Hence, the reqd. no. of signals
= 20 + 60 + 120 + 120
= 320.
Question 5:
Evaluate :
5!
Answer:
5! = 5 × 4 × 3 × 2 × 1 = 120.
Question 6:
Evaluate :
7!
Answer:
7! = 7 × 6 × 5 × 4 × 3 × 1= 5040.
Question 7:
Evaluate :
7! – 5!
Answer:
7! – 5! = 5040 – 120 = 4920
Question 8:
Compute :
Answer:
Question 9:
Compute :
Answer:
Question 10:
Answer:
Question 11:
Answer:
Question 12:
Find the number of permutations of the
letters of the word :
ALLAHABAD.
Answer:
Question 13:
How many 4-digit numbers can be formed using the digits 1 to 9 if repetition of digits is not allowed ?
Answer:
Question 14:
How many numbers lying between 100 and 1000 can be formed with digits 0, 1, 2, 3, 4, 5, if repetition of the digits is not allowed ?
Answer:
Question 15:
Find the value of n such that :
Answer:
Question 16:
Find the value of n such that :
Answer:
3n = 5(n – 4)
[_ (n – 1) (n – 2) (n – 3) 0 as n > 4]
2n = 20.
Hence, n = 10.
Question 17:
Answer:
Question 18:
Find the number of different 8-letter
arrangements that can be made from the letters of
the word DAUGHTER so that :
(i) all vowels come together (ii) all vowels do not
occur together.
Answer:
Question 19:
In how many ways can 4 red, 3 yellow and 2 green discs be arranged in a row if the discs of the same colours are indistinguishable ?
Answer:
Question 20:
Find the number of arrangements of the letters of the word ‘INDEPENDENCE’. In how many of these arrangements, do the words start with P ?
Answer:
Question 21:
Find the number of arrangements of the letters of the word ‘INDEPENDENCE’. In how many of these arrangements, do all the vowels always occur together ?
Answer:
Question 22:
Find the number of arrangements of the letters of the word ‘INDEPENDENCE’. In how many of these arrangements, do the vowels never occur together ?
Answer:
Reqd. number of arrangements = Number of arrangements without any restriction – Number of arrangements when vowels occur together = 1663200 – 16800 [Using parts (i) & (ii)] = 1646400.
Question 23:
Find the number of arrangements of the letters of the word ‘INDEPENDENCE’. In how many of these arrangements, do the words begin with I and end in P ?
Answer:
Question 24:
Answer:
Question 25:
A committee of 3 persons is to be constituted from a group of 2 Men and 3 Women. In how many ways can this be done ? How many of these committees would consist of 1 Man and 2 Women ?
Answer:
Question 26:
What is the number of ways of
choosing 4 cards from a pack of 52 playing
cards ? In how many of these :
four cards are of the same suit ?
Answer:
Question 27:
What is the number of ways of
choosing 4 cards from a pack of 52 playing
cards ? In how many of these :
four cards belong to four different suits ?
Answer:
Question 28:
What is the number of ways of
choosing 4 cards from a pack of 52 playing
cards ? In how many of these :
are face cards ?
Answer:
Question 29:
What is the number of ways of
choosing 4 cards from a pack of 52 playing
cards ? In how many of these :
two are red cards and two are black cards ?
Answer:
Question 30:
What is the number of ways of
choosing 4 cards from a pack of 52 playing
cards ? In how many of these :
cards are of the same colour ?
Answer:
Question 31:
How many words, with or without meaning, each of 3 vowels and 2 consonants can be formed from the letters of the word ‘INVOLUTE’.
Answer:
The word ‘INVOLUTE’ has 4 vowels viz.
I, O, E and U and has 4 consonants viz. N, V, L and T.
Number of ways of selecting 3 vowels out of 4
= 4C3 = 4.
Number of ways of selecting 2 consonants out of 4
= 4C2 = 6.
Number of combinations of 3 vowels and 2 constants
= 4 × 6 = 24.
Each of 24 combinations has 5 letters, which can be
arranged among themselves in 5! ways.
Hence, the required number of different words = 24 × 5!
= 24 × 120 = 2880.
Question 32:
A group consists of 4 girls and 7
boys. In how many ways can a team of 5 members be
selected if the team has :
no girl
Answer:
Question 33:
A group consists of 4 girls and 7
boys. In how many ways can a team of 5 members be
selected if the team has :
at least one boy and one girl
Answer:
Question 34:
A group consists of 4 girls and 7
boys. In how many ways can a team of 5 members be
selected if the team has :
at least 3 girls
Answer:
Question 35:
Find the number of words with or without meaning, which can be made using all the letters of the word ‘AGAIN’. If these words are written as in the dictionary, what will be the 50th word ?
Answer:
Question 36:
How many numbers greater than 1000000 can be formed by using the digits 1, 2, 6, 2, 4, 2, 4 ?
Answer:
Question 37:
In how many ways can 5 girls and 3 boys be seated in a row so that no two boys are together ?
Answer:
Question 38:
How many 3-digit numbers can be formed from the
digits 1, 2, 3, 4 and 5 assuming :
repetition of digits allowed
Answer:
To form a number of three digits, we are to fill
up three places viz. the hundred’s, the ten’s and the unit’s.
The hundred’s place can be filled in 5 different ways.
Similarly ten’s place and unit’s place can also be filled in
5 different ways each.
Associating, by the Principle of Counting,
the no. of three digit numbers = 5 × 5 × 5
= 125.
Question 39:
How many 3-digit numbers can be formed from the
digits 1, 2, 3, 4 and 5 assuming :
repetition of digits not allowed ?
Answer:
To form a number of three digits, we are to fill up three places viz. the hundred’s, the ten’s and the unit’s. The hundred’s place can be filled in 5 different ways. The ten’s place can be filled in 4 different ways. The unit’s place can be filled in 3 different ways. Associating, by the Principle of Counting, the no. of three-digit numbers = 5 × 4 × 3 = 60.
Question 40:
How many 3-digit even numbers can be formed from the digits 1, 2, 3, 4, 5, 6 if the digits can be repeated?
Answer:
Let us fix ‘2’ at unit’s place.
Now ten’s and hundred’s places can be filled up in 6
ways each [_ Repetition is allowed]
No. of numbers having ‘2’ at unit’s place = 6 × 6 = 36.
Similarly no. of numbers having ‘4’ at unit’s place = 36
and no. of numbers having ‘6’ at unit’s place = 36.
Hence, the total number of 3-digit even numbers
= 36 + 36 + 36 = 108.
Question 41:
How many 4-letter code words are possible using the first 10 letters of the English alphabet, if no letter can be repeated ?
Answer:
First letter is filled in 10 ways.
Second letter is filled in 9 ways.
Third letter is filled in 8 ways.
Fourth letter is filled in 7 ways.
Associating, by the Principle of Counting.
the reqd. no. of ways = 10 × 9 × 8 × 7
= 5040.
Question 42:
How many 5-digit telephone numbers can be constructed using the digits 0 to 9 if each number starts with 67, for example 67125; etc. and no digit appears more than once ?
Answer:
Here third place can be filled up in 8 ways. Fourth place can be filled up in 7 ways and fifth place can be filled up in 6 ways. Associating, by the Principle of counting, the reqd. no. of telephone numbers = 8 × 7 × 6 = 336.
Question 43:
A coin is tossed 3 times and the outcomes are recorded.
How many possible outcomes are there ?
Answer:
There are two outcomes on each toss of a coin.
No. of outcomes = 2 × 2 × 2 = 23 = 8.
Question 44:
Given 5 flags of different colours, how many different signals can be generated if the signal requires the use of two flags, one below the other ?
Answer:
First flag can be selected in 5 different ways. Second flag can be selected in 4 different ways. Associating, by the Principle of Counting. the reqd. no. of signals generated = 5 × 4 = 20.
Question 45:
Evaluate :
8 !
Answer:
8 ! = 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 40320.
Question 46:
Evaluate :
4 ! – 3 !
Answer:
4 ! – 3 ! = 4 × 3 × 2 × 1 – 3 × 2 × 1 = 24 – 6 = 18.
Question 47:
Is 3 ! + 4 ! = 7 ! ?
Answer:
3 ! = 3 × 2 × 1 = 6.
4 ! = 4 × 3 × 2 × 1 = 24.
LHS = 3 ! + 4 ! = 6 + 24 = 30.
RHS = 7 ! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040.
Hence, 3 ! + 4 ! 7 !
Question 48:
Answer:
Question 49:
Answer:
Question 50:
n = 6, r = 2
Answer:
Question 51:
n = 9, r = 5
Answer:
Question 52:
How many 3-digit numbers can be formed by using the digits 1 to 9 if no digit is repeated ?
Answer:
The given digits are 1, 2, 3, ...., 9.
3-digit numbers if no digit is repeated
= 9P3 = 9 × 8 × 7 = 504.
Question 53:
How many four-digit numbers are there, with no digit repeated ?
Answer:
We have the digits :
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
No. of 4-digit numbers = 10P4
= 10 × 9 × 8 × 7 = 5040.
But out of these, we are to neglect the numbers having 0
at the extreme left because, then, these numbers will have 3
instead of 4 digits.
Fix 0 at extreme left : 0 × × ×
Now the remaining three places can be filled up in 9P3
i.e. 9 × 8 × 7 = 504 ways.
Hence, the reqd. no. of numbers
= 5040 – 504 = 4536.
Question 54:
How many 3-digit even numbers can be made using the digits 1, 2, 3, 4, 5, 6, 7 if no digit is repeated ?
Answer:
Unit place can be filled by 2 or 4 or 6 in 3 ways.
Other two places can be filled by remaining 5 digits in 5P2
i.e. 5 × 4 i.e. 20 ways.
Reqd. number of 3-digit even numbers = 3 × 20 = 60.
Question 55:
Find the number of 4-digit numbers that can be formed using the digits 1, 2, 3, 4, 5 if no digit is repeated. How many of these numbers will be even ?
Answer:
(i) No. of 4-digit numbers = 5P4
= 5 × 4 × 3 × 2 = 120.
(ii) The unit’s place can be filled in two ways.
The other three places can be filled in 4P3 = 4 × 3 × 2 = 24
ways.
Associating, the number of 4-digit even numbers = 2 × 24
= 48.
Question 56:
From a committee of 8 persons, in how many ways can we choose a chairman and vice-chairman, assuming one person cannot hold more than one position.
Answer:
There are 8 persons.
Chairman and Vice-chairman can be chosen in 8P2
i.e. 8 × 7 i.e. 56 ways.
Question 57:
Answer:
Question 58:
Answer:
Question 59:
Answer:
Question 60:
How many words, with or without meanings, can be formed using all the letters of the word ‘EQUATION’, using each letter exactly once ?
Answer:
The given word is ‘EQUATION’.
Here n, the total number of words = 8.
Hence, the reqd. number of different words
= 8P8 = 8 ! = 8.7.6.5.4.3.2.1= 40320.
Question 61:
How many words (with or without dictionary meaning)
can be made from the letters of the word ‘MONDAY’,
assuming that no letter is repeated if :
4 letters are used at a time ?
Answer:
The word ‘MONDAY’ has 6 letters.
Question 62:
How many words (with or without dictionary meaning)
can be made from the letters of the word ‘MONDAY’,
assuming that no letter is repeated if :
all letters are used at a time ?
Answer:
The word ‘MONDAY’ has 6 letters.
The number of words when all letters are used at a
time = 6P6 = 6 ! = 720.
Question 63:
How many words (with or without dictionary meaning)
can be made from the letters of the word ‘MONDAY’,
assuming that no letter is repeated if :
all letters are used but the first is a vowel ?
Answer:
The word ‘MONDAY’ has 6 letters.
The first letter in each permutation is either ‘O’ or ‘A’
(vowel), which can be possible in 2 ways.
The remaining five letters can be used without any
restriction, which can be done in 5P5 = 5 ! = 120 ways.
Required number of words
= 2 × 120 = 240.
Question 64:
In how many of the distinct permutations of the letters in MISSISSIPPI do the four I’s not come together ?
Answer:
Question 65:
In how many ways can the letters of the word
‘PERMUTATIONS’ be arranged if the :
words start with P and end with S
Answer:
When the words start with P and end with S P × × × × × × × × × × S Between P and S, there are 10 places, which are to be filled up. Out of these, T is repeated twice.
Question 66:
In how many ways can the letters of the word
‘PERMUTATIONS’ be arranged if the :
vowels are all together
Answer:
When vowels are all together.
The vowels EUAIO can be taken as one word.
These can be arranged among themselves in 5 ! i.e. 120
ways.
Now we have eight letters, out of which, T is repeated
twice, which can be arranged in
= 120 × 20160 = 2419200.
Question 67:
In how many ways can the letters of the word
‘PERMUTATIONS’ be arranged if the :
there are always 4 letters between P and S ?
Answer:
That are 12 letters, which are to be arranged in 12 places,
Question 68:
Answer:
Question 69:
Answer:
(2n – 1) (n – 1) = 9(n – 1) 2n – 1 = 9 [n 1] 2n = 10 n = 5.
Question 70:
Answer:
Question 71:
How many chords can be drawn through 21 points on a circle ?
Answer:
Question 72:
In how many ways can a team of 3 boys and 3 girls be selected from 5 boys and 4 girls.
Answer:
Question 73:
Find the number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls if each selection consists of 3 balls of each colour.
Answer:
Question 74:
Determine the number of 5 card combinations out of a deck of 52 cards if there is exactly one ace in each combination.
Answer:
Question 75:
In how many ways can we select a cricket eleven from 17 players in which only 5 players can bowl if cricket team must include exactly 4 bowlers.
Answer:
There are 17 players in which 5 are bowlers and
12 are non-bowlers.
Each team includes 4 bowlers and 7 non-bowlers.
Question 76:
A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected.
Answer:
Question 77:
In how many ways can a student choose 5 courses out of 9 courses if two courses are compulsory for each student ?