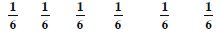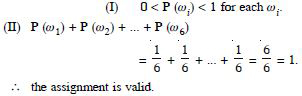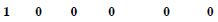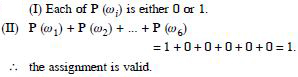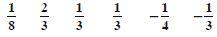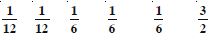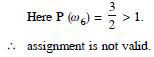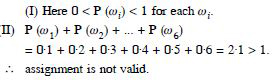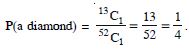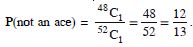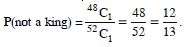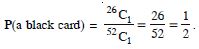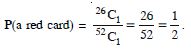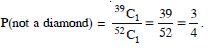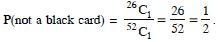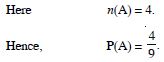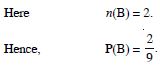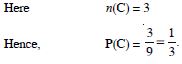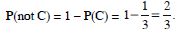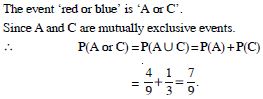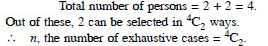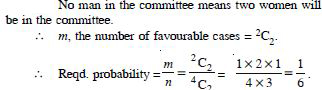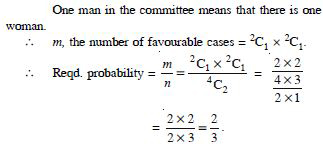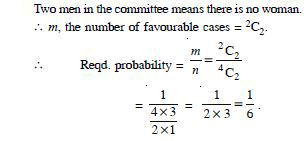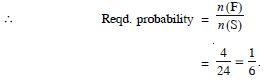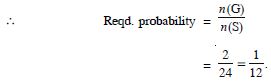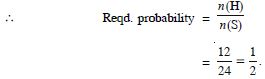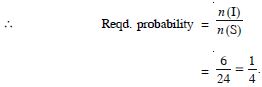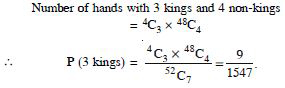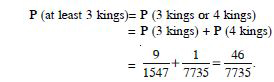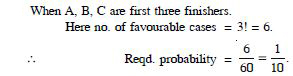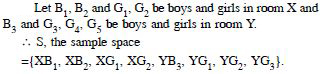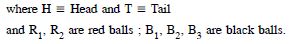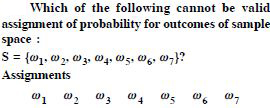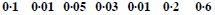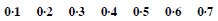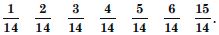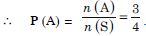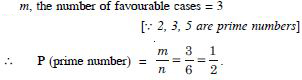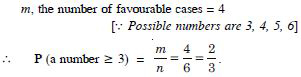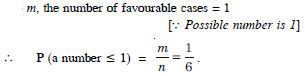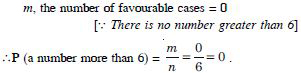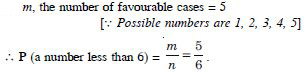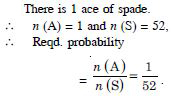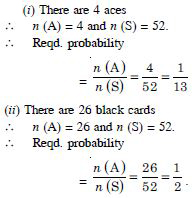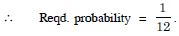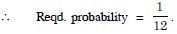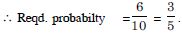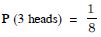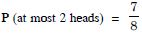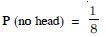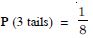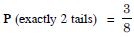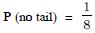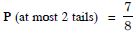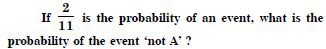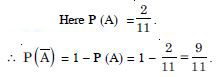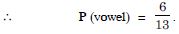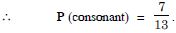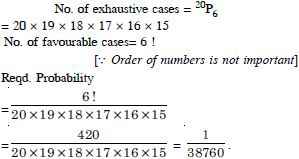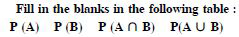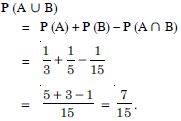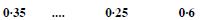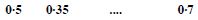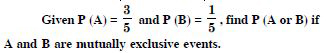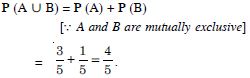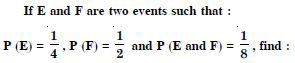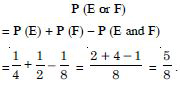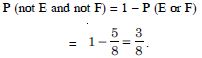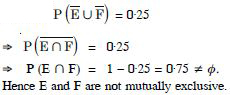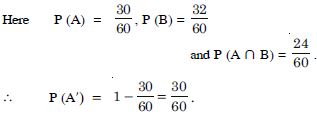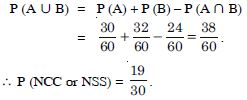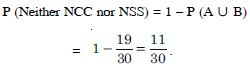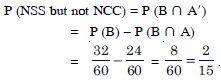Grab access to free NCERT Solutions available on Aasoka for Class 11 students. Practice Maths’ equation regularly and master the concepts of the chapter “Probability”. The subject matter experts have prepared the solutions keeping the latest CBSE syllabus in mind. Therefore, if you are looking for quality study material for the preparation for exams, NCERT Solutions for Class 11 is the key to it. Boost your overall performance now for scoring good marks in the exams.
In the chapter “Probability” of Maths Class 11 students will learn the probability of an event, the occurrence of events, outcomes of random experiments, connections with the theories of earlier classes, axiomatic probability, and much more.
Question 1:
Two coins (a one rupee coin and two rupee coin) are tossed once. Find a sample space.
Answer:
Sample space = {HH, HT, TH, TT}, where H Head and T Tail.
Question 2:
Find the sample space associated with the experiment of rolling a pair of dice (one is blue and the other red) once. Also, find the number of elements of this sample space.
Answer:
(i) Sample space = {(1, 1), (1, 2),.......,(1, 6) ;
(2, 1), (2, 2),.........,(2, 6) ; (6, 1), (6, 2),.........., (6, 6)}.
(ii) No. of elements = 6 × 6 = 36.
Question 3:
In the following experiment, specify the
appropriate sample space :
A boy has a 1 rupee coin, a 2 rupee coin and a 5
rupee coin in his pocket. He takes two coins out of his
pocket, one after the other.
Answer:
Let Q denote a 1 rupee coin, H a 2 rupee
coin and R a 5 rupee coin.
The first coin may be any one of Q, H and R.
Corresponding to Q, the second draw may be H or R.
Thus the two draws may be QH or QR.
Similarly corresponding to H, the second draw be Q or
R. Thus the two draws may be HQ or HR.
Lastly the two draws may be RH or RQ.
Hence, the sample space
= {QH, QR, HQ, HR, RH, RQ}.
Question 4:
In the following experiment, specify the
appropriate sample space :
A person is noting down the number of accidents
along a busy highway during a year.
Answer:
The number of accidents can be 0 or 1 or 2; and so
on.
Sample space = {0, 1, 2, ... }.
Question 5:
A coin is tossed. If it shows head, we draw a ball from a bag containing of 3 blue and 4 white balls ; if it shows tail we throw a dice. Describe the sample space of this experiment.
Answer:
Question 6:
Consider the experiment in which a coin is tossed repeately until a head comes up. Describe the sample space.
Answer:
Sample space = {H, TH, TTH, TTTH, TTTTH,.......},
where H Head and
T Tail.
Question 7:
Consider the experiment of rolling a dice.
Let A be the event ‘getting a prime number’, B be the event
‘getting an odd number’. Write the sets representing the
events :
A or B
Answer:
Here S = {1, 2, 3, 4, 5, 6}, A = {2, 3, 5} and
B = {1, 3, 5}.
‘A or B’ = A B = {1, 2, 3, 5}.
Question 8:
Consider the experiment of rolling a dice.
Let A be the event ‘getting a prime number’, B be the event
‘getting an odd number’. Write the sets representing the
events :
A and B
Answer:
Here S = {1, 2, 3, 4, 5, 6}, A = {2, 3, 5} and
B = {1, 3, 5}.
‘A and B’ = A B = {3, 5}.
Question 9:
Consider the experiment of rolling a dice. Let A be the event ‘getting a prime number’, B be the event ‘getting an odd number’. Write the sets representing the events :
A but not BAnswer:
Here S = {1, 2, 3, 4, 5, 6}, A = {2, 3, 5} and
B = {1, 3, 5}.
‘A but not B’ = A – B = {2}.
Question 10:
Consider the experiment of rolling a dice.
Let A be the event ‘getting a prime number’, B be the event
‘getting an odd number’. Write the sets representing the
events :
not A
Answer:
Here S = {1, 2, 3, 4, 5, 6}, A = {2, 3, 5} and
B = {1, 3, 5}.
‘not A’ = A′ = {1, 4, 6}.
Question 11:
Two dice are thrown and the sum of
the numbers which come up on the dice is noted.
Let us consider the following events associated
with this experiment.
- ‘the sum is even’
- ‘the sum is a multiple of 3’
- ‘the sum is less than 4’
- ‘the sum is greater than 11”.
Which pairs are mutually exclusive and which are not ?
Answer:
We have 36 elements in the sample space :
S = {(x, y) : x, y = 1, 2, 3, 4, 5, 6}.
A = {(1, 1), (1, 3), (1, 5), (2, 2), (2, 4), (2, 6),
(3, 1), (3, 3), (3, 5), (4, 2), (4, 4), (4, 6),
(5, 1), (5, 3), (5, 5), (6, 2), (6, 4), (6, 6)}
[_ 1 + 1 = 2 (even) ; etc.]
B = {(1, 2), (2, 1), (1, 5), (5, 1), (3, 3), (2, 4), (4, 2),
(3, 6), (6, 3), (4, 5), (5, 4), (6, 6)}
[_ 1 + 2 = 3, which is a multiple of 3 ; etc.]
C = {(1, 1), (1, 2), (2, 1)} [_ 1 + 1 = 2 < 4 ; etc.]
D = {(6, 6)}. [ 6 + 6 = 12 > 11]
Now A B = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1),
(6, 6)}
A and B are not mutually exclusive events.
Similarly A C , A D , B C
and B D .
Thus the pairs (A, C), (A, D), (B, C) and (B, D) are not
mutually exclusive
But C D = and as each C, D are mutually exclusive
events.
Question 12:
A coin is tossed three times.
Consider the following events :
- No head appears
- Exactly one head appears
- Atleast two heads appear
Do they form a set of mutually exclusive and exhaustive events ?
Answer:
The sample space is :
S = {HHH, HHT, HTH, THH, HTT, THT,
TTH, TTT}.
Here A= {TTT}, B = {HTT, THT, TTH}
and C= {HHT, HTH, THH, HHH}.
(i) Now ABC = {TTT, HTT, THT, TTH,
HHT, HTH, THH, HHH} = S.
A, B and C are exhaustive events.
(ii) A B = , B C = and A C =
events are pair-wise disjoint
events are mutually exclusive.
Hence, A, B and C form a set of mutually exclusive and
exhaustive events.
Question 13:
Answer:
Question 14:
Answer:
Question 15:
Answer:
Question 16:
Answer:
Question 17:
Answer:
Question 18:
One card is drawn from a well-shuffled
deck of 52 cards. If each outcome is equally likely, calculate
the probability that the card will be :
a diamond
Answer:
Question 19:
One card is drawn from a well-shuffled
deck of 52 cards. If each outcome is equally likely, calculate
the probability that the card will be :
not an ace
Answer:
Question 20:
One card is drawn from a well-shuffled
deck of 52 cards. If each outcome is equally likely, calculate
the probability that the card will be :
not a king
Answer:
Question 21:
One card is drawn from a well-shuffled
deck of 52 cards. If each outcome is equally likely, calculate
the probability that the card will be :
a black card (a club or a spade)
Answer:
Question 22:
One card is drawn from a well-shuffled
deck of 52 cards. If each outcome is equally likely, calculate
the probability that the card will be :
a red card
Answer:
Question 23:
One card is drawn from a well-shuffled
deck of 52 cards. If each outcome is equally likely, calculate
the probability that the card will be :
not a diamond
Answer:
Question 24:
One card is drawn from a well-shuffled
deck of 52 cards. If each outcome is equally likely, calculate
the probability that the card will be :
not a black card
Answer:
Question 25:
A bag contains 9 discs of which 4 are
red, 3 are blue and 2 are yellow. The discs are similar in
shape and size. A disc is drawn at random from the bag.
Calculate the probability that it will be :
red
Answer:
Total number of discs = 4 + 3 + 2 = 9.
Let the events A, B and C be :
A : Disc drawn is red
B : Disc drawn is yellow
and C : Disc drawn is blue.
Question 26:
A bag contains 9 discs of which 4 are
red, 3 are blue and 2 are yellow. The discs are similar in
shape and size. A disc is drawn at random from the bag.
Calculate the probability that it will be :
yellow
Answer:
Total number of discs = 4 + 3 + 2 = 9.
Let the events A, B and C be :
A : Disc drawn is red
B : Disc drawn is yellow
and C : Disc drawn is blue.
Question 27:
A bag contains 9 discs of which 4 are
red, 3 are blue and 2 are yellow. The discs are similar in
shape and size. A disc is drawn at random from the bag.
Calculate the probability that it will be :
blue
Answer:
Total number of discs = 4 + 3 + 2 = 9.
Let the events A, B and C be :
A : Disc drawn is red
B : Disc drawn is yellow
and C : Disc drawn is blue.
Question 28:
A bag contains 9 discs of which 4 are
red, 3 are blue and 2 are yellow. The discs are similar in
shape and size. A disc is drawn at random from the bag.
Calculate the probability that it will be :
not blue
Answer:
Total number of discs = 4 + 3 + 2 = 9.
Let the events A, B and C be :
A : Disc drawn is red
B : Disc drawn is yellow
and C : Disc drawn is blue.
Question 29:
A bag contains 9 discs of which 4 are
red, 3 are blue and 2 are yellow. The discs are similar in
shape and size. A disc is drawn at random from the bag.
Calculate the probability that it will be :
either red or blue
Answer:
Total number of discs = 4 + 3 + 2 = 9.
Let the events A, B and C be :
A : Disc drawn is red
B : Disc drawn is yellow
and C : Disc drawn is blue.
Question 30:
Two students Anil and Ashima
appeared in an examination. The probability that
Anil will qualify the examination is 0·05 and that
Ashima will qualify the examination is 0·10. The
probability that both will qualify the examination
is 0·02. Find the probability that :
both Anil and Ashima will not qualify the
examination
Answer:
Let A and B be two events :
A : Anil will qualify the examination
B : Ashima will qualify the examination.
We have : P (A) = 0·05, P (B) = 0·10 and
P (A B) = 0·02.
A′ is ‘not A’ and B′ is ‘not B’.
‘Both Anil and Ashima will not qualify the examination’
may be expressed as A′ B′.
Also A′ B′ = (A B)′
[By De–Morgan’s Law]
Now P (A B) = P (A) + P (B) – P (A B)
= 0·05 + 0·10 – 0·02 = 0·13
P (A′ B′) = P (A B)′ = 1 – 0·13 = 0·87.
Hence, the probability that both Anil and Ashima will
not qualify the examination = 0·87.
Question 31:
Two students Anil and Ashima
appeared in an examination. The probability that
Anil will qualify the examination is 0·05 and that
Ashima will qualify the examination is 0·10. The
probability that both will qualify the examination
is 0·02. Find the probability that :
atleast one of them will not qualify the
examination
Answer:
Let A and B be two events :
A : Anil will qualify the examination
B : Ashima will qualify the examination.
We have : P (A) = 0·05, P (B) = 0·10 and
P (A B) = 0·02.
P (at least one of Anil and Ashima will not qualify)
= P (A B′ or A′ B or A′ B′)
But S = {AB, AB′, A′B, A′B′}
P (A B) + P (A B′) + P (A′ B)
+ P (A′ B′) = 1
P (A B′) + P (A′ B) + P (A′ B′)
= 1 – P (A B)
= 1 – 0·02 = 0·98.
Hence, the probability that at least one of Anil and
Ashima will not qualify = 0·98.
Question 32:
Two students Anil and Ashima
appeared in an examination. The probability that
Anil will qualify the examination is 0·05 and that
Ashima will qualify the examination is 0·10. The
probability that both will qualify the examination
is 0·02. Find the probability that :
only one of them will qualify the examination
Answer:
Let A and B be two events :
A : Anil will qualify the examination
B : Ashima will qualify the examination.
We have : P (A) = 0·05, P (B) = 0·10 and
P (A B) = 0·02.
P (only one of them will qualify)
= P (A B′ or A′ B)
= P (A B′) + P (A′ B)
= P (A) – P (A B) + P (B)
– P (A B)
= 0·10 – 0·02 + 0·05 – 0·02 = 0·11.
Hence, the probability that only one of Anil and
Ashima will qualify = 0·11.
Question 33:
A committee of two is selected from
two men and two women. What is the probability
that the committee will have :
no man
Answer:
Question 34:
A committee of two is selected from
two men and two women. What is the probability
that the committee will have :
one man
Answer:
Question 35:
A committee of two is selected from
two men and two women. What is the probability
that the committee will have :
two men ?
Answer:
Question 36:
On her vacation Veena visits four cities
(A, B, C and D) in a random order. What is the probability
that she visits :
A before B ?
Answer:
The number of arrangements in which Veena
can visit four cities (A, B, C and D) = 4 ! = 24.
Thus S = {ABCD, ABDC, ACBD, ACDB, ADBC,
ADCB, BACD, BADC, BDAC, BDCA, BCAD, BCDA,
CABD, CADB, CBDA, CBAD, CDAB, CDBA, DABC,
DACB, DBCA, DBAC, DCAB, DCBA}.
Let E be event when Veena visits ‘A before B’
Then E = {ABCD, ABDC, ACBD, ACDB, ADBC,
ADCB, CABD, CADB, CDAB, DABC, DACB, DCAB}
Question 37:
On her vacation Veena visits four cities
(A, B, C and D) in a random order. What is the probability
that she visits :
A before B and B before C ?
Answer:
The number of arrangements in which Veena
can visit four cities (A, B, C and D) = 4 ! = 24.
Thus S = {ABCD, ABDC, ACBD, ACDB, ADBC,
ADCB, BACD, BADC, BDAC, BDCA, BCAD, BCDA,
CABD, CADB, CBDA, CBAD, CDAB, CDBA, DABC,
DACB, DBCA, DBAC, DCAB, DCBA}.
Let F be the event when Veena visits A before B and
B before C.
Then F = {ABCD, ABDC, ADBC, DABC}.
Question 38:
On her vacation Veena visits four cities (A, B, C and D) in a random order. What is the probability that she visits :
A first and B last ?Answer:
The number of arrangements in which Veena
can visit four cities (A, B, C and D) = 4 ! = 24.
Thus S = {ABCD, ABDC, ACBD, ACDB, ADBC,
ADCB, BACD, BADC, BDAC, BDCA, BCAD, BCDA,
CABD, CADB, CBDA, CBAD, CDAB, CDBA, DABC,
DACB, DBCA, DBAC, DCAB, DCBA}.
Let G be the event when Veena visits A first and B
last.
Then G = {ACDB, ADCB}
Question 39:
On her vacation Veena visits four cities
(A, B, C and D) in a random order. What is the probability
that she visits :
A either first or second ?
Answer:
The number of arrangements in which Veena
can visit four cities (A, B, C and D) = 4 ! = 24.
Thus S = {ABCD, ABDC, ACBD, ACDB, ADBC,
ADCB, BACD, BADC, BDAC, BDCA, BCAD, BCDA,
CABD, CADB, CBDA, CBAD, CDAB, CDBA, DABC,
DACB, DBCA, DBAC, DCAB, DCBA}.
Let H be the event when Veena visits A either first
or second.
Then H = {ABCD, ABDC, ACBD, ACDB, ADBC,
ADCB,
BACD, BADC, CABD, CADB, DABC, DACB}.
Question 40:
On her vacation Veena visits four cities
(A, B, C and D) in a random order. What is the probability
that she visits :
A just before B ?
Answer:
The number of arrangements in which Veena
can visit four cities (A, B, C and D) = 4 ! = 24.
Thus S = {ABCD, ABDC, ACBD, ACDB, ADBC,
ADCB, BACD, BADC, BDAC, BDCA, BCAD, BCDA,
CABD, CADB, CBDA, CBAD, CDAB, CDBA, DABC,
DACB, DBCA, DBAC, DCAB, DCBA}.
Let I be the event when Veena visits A just
before B.
Then I = {ABCD, ABDC, CABD, CDAB, DABC,
DCAB}.
Question 41:
Find the probability that when a hand of
7 cards is drawn from a well shuffled deck of 52 cards, it
contains :
all kings
Answer:
Total number of possible hands = 52C7.
Question 42:
Find the probability that when a hand of
7 cards is drawn from a well shuffled deck of 52 cards, it
contains :
3 kings
Answer:
Total number of possible hands = 52C7.
Question 43:
Find the probability that when a hand of
7 cards is drawn from a well shuffled deck of 52 cards, it
contains :
at least 3 kings
Answer:
Total number of possible hands = 52C7.
Question 44:
If A, B, C be three events associated
with a random experiment, line that :
P (A B C) = P (A) + P (B) + P (C) – P (A B) –
P (B C) – P (A C) + P (A B C).
Answer:
Proof. Let B C = D
Then P (A B C) = P (A D) = P (A) + P
(D) – P (A D) ...(1) [Th. IV]
But A D = A (B C)
= (A B) (A C)
P (A D) = P [(A B) (A C)]
= P (A B) + P (A C) – P
[(A B) (A C)] [Th. VI]
= P (A B + P (A C) – P
(A B C) ...(2)
[(A B) (A C) = A B C]
and P (D) = P (B C) = P (B) + P (C) – P (B C)
...(3)
From (1), using (2) and (3), we have :
P (A B C) = P (A) + P (B) + P (C) – P
(B C) – [P (A B) + P (A C) – P (A B C)]
= P (A) + P (B) + P (C) – P
(A B) – P (B C) – P (A C) + P (A B C).
Cor. If A, B, C are mutually exclusive events, then
P (A B) = P (B C) = P (A C)
= P (A B C) = 0.
P (A B C) = P (A) + P (B) + P (C).
Question 45:
In a relay race there are five teams A, B,
C, D and E.
What is the probability that A, B and C finish first,
second and third respectively ?
(Assume that all finishing orders are equally likely.).
Answer:
No. of elements in sample space = 5P3
= 5 × 4 × 3
= 60.
Question 46:
In a relay race there are five teams A, B,
C, D and E.
What is the probability that A, B and C are first
three to finish (in any Order) ?
(Assume that all finishing orders are equally likely.).
Answer:
No. of elements in sample space = 5P3
= 5 × 4 × 3
= 60.
Question 47:
In each of the following, describe the sample space for the indicated experiment
:
A coin is tossed three times.
Answer:
When a coin is tossed three times, then the possible
outcomes of the experiment are :
HHH, HHT, HTH, THH, HTT, THT, TTH, TTT,
where H Head and T Tail.
S, the sample sapce
={HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}.
Question 48:
In each of the following, describe the sample space for the indicated experiment
:
A die is thrown two times.
Answer:
When a die is thrown two times.
S, the sample space={(1, 1), (1, 2), ........., (1, 6) ; (2,
1), (2, 2), ...... (2, 6) ;
................................. ; (6, 1), (6, 2), ...........
(6, 6)}.
Question 49:
In each of the following, describe the sample space for the indicated experiment
:
A coin is tossed four times.
Answer:
When a coin is tossed four times.
S, the sample space
= {HHHH, HHHT, HHTH, HTHH, THHH, HHTT, HTHT,
HTTH,
THHT, THTH, TTHH, HTTT, THTT, TTHT, TTTH,
TTTT},
where H Head and T Tail.
Question 50:
In each of the following, describe the sample space for the indicated experiment
:
A coin is tossed and a die is thrown.
Answer:
When a coin is tossed and a die is thrown.
S, the sample space
= {H1, H2, H3, H4, H5, H6, T1, T2, T3,
T4, T5, T6},
where H Head and T Tail.
Question 51:
In each of the following, describe the sample space for the indicated experiment
:
A coin is tossed and then a die is rolled only in case
a head is shown on the coin.
Answer:
When a coin is tossed and a die is rolled only in case a
head is shown on the coin.
S, the sample space
={H1, H2, H3, H4, H5, H6, T},
where H Head and T Tail.
Question 52:
In each of the following, describe the sample space for the indicated experiment
:
2 boys and 2 girls are in Room X and 1 boy and
3 girls in room Y. Specify the sample space for the
experiment in which a room is selected and then a person.
Answer:
Question 53:
In each of the following, describe the sample space for the indicated experiment
:
One die of red colour, one of white colour and
one of blue colour are placed in a bag. One die is
selected at random and rolled, its colour and the
number on its upper most face is noted. Describe
the sample space.
Answer:
Let R, W and B denote the red, white and blue die
respectively.
S, the sample space
= {R1, R2, R3, R4, R5, R6, W1, W2, W3, W4,
W5, W6, B1, B2, B3, B4, B5, B6}.
Question 54:
An experiment consists of recording boy-girl
composition of families with 2 children.
What is the sample space if we are interested in
knowing whether it is a boy or a girl in the order of their
births ?
Answer:
S, the required sample space
= {BB, BG, GB, GG},
where B Boy and G Girl.
Question 55:
An experiment consists of recording boy-girl
composition of families with 2 children.
What is the sample space if we are interested in the
number of girls in the family ?
Answer:
S, the required sample space
= {0, 1, 2}.
Question 56:
A box contains 1 red and 3 identical white balls.
Two balls are drawn at random in succession without
replacement. Write the sample space for this experiment.
Answer:
The box contains 1 red and 3 identical white balls.
S, the reqd. sample space
= {RW, WR, WW}.
where R Red ball and W White ball.
Question 57:
An experiment consists of tossing a coin and then throwing it second time if a head occurs. If a tail occur on the first toss, then a die is rolled once. Find the sample space.
Answer:
S, the reqd. sample space.
= {HH, HT, T1, T2, T3, T4, T5, T6},
where H Head and T Tail.
Question 58:
Suppose 3 bulbs are selected at random from a lot.
Each bulb is tested and classified as defective (D) or nondefective
(N). Write the sample space of this experiment.
Answer:
S, the reqd. sample space
= {DDD, DDN, DND, NDD, DNN, NDN, NND, NNN},
where D Defective bulb and N Non-defective bulb.
Question 59:
A coin is tossed. If the outcome is a head, a die is thrown. If the die shows up an even number, then die thrown again. What is the sample space for the experiment ?
Answer:
S, the reqd. sample space.
= {T, H1, H3, H5, H21, H22, H23, H24,
H25, H26, H41, H42, H43, H44, H45, H46,
H61, H62, H63, H64, H65, H66},
where H Head and T Tail.
Question 60:
The numbers 1, 2, 3 and 4 are written separately on four slips of paper. The slips are put in a box mixed thoroughly. A person draws two slips from the box, one after the other, without replacement. Describe the sampe space for the experiment.
Answer:
S, the sample space
= {(1, 2), (1, 3), (1, 4), (2, 1), (2, 3), (2, 4),
(3, 1), (3, 2), (3, 3), (4, 1), (4, 2), (4, 3)}.
Question 61:
An experiment consists of rolling a die and then tossing a coin once if the number on the die is even. If the number on the die is odd, the coin is tossed twice. Write the sample space for this experiment.
Answer:
S, the reqd. sample space is :
{1HH, 1TH, 1HT, 1TT, 2H, 2T, 3HH, 3TH, 3HT, 3TT,
4H, 4T, 5HH, 5TH, 5HT, 5TT, 6H, 6T},
where H Head and T Tail.
Question 62:
A coin is tossed. If it shows a tail, we draw a ball from the box which contains 2 red and 3 black balls. If it shows head, we throw a die. Find the sample space for this experiment.
Answer:
Question 63:
A die is thrown repeatedly until a six comes up.
What is the sample space for this experiment ?
Answer:
S, the reqd. sample space
= {6, (1, 6) (2, 6), (3, 6), (4, 6), (5, 6),
(1, 1, 6), (1, 2, 6), (1, 3, 6), ....... (1, 5, 6),
(2, 1, 6), (2, 2, 6), ..........., (2, 5, 6), ..........
(5, 1, 6), (5, 2, 6), .............}.
Question 64:
A die is rolled. Let E be the event ‘‘die shows 4’’ and F be the event ‘‘die shows even number’’. Are E and F mutually exclusive ?
Answer:
Here sample space,
S = {1, 2, 3, 4, 5, 6}.
E (die shows 4) = {4}.
F (die shows an even number} = {2, 4, 6}.
Here H F = {4} E F .
Hence E and F are not mutually exclusive.
Question 65:
A die is thrown. Observe the number that appears
on the top face. Describe the following events :
(i) A : a number less than 7
(ii) B : a number greater than 7
(iii) C : a multiple of 3
(iv) D : a number less than 4
(v) E : an even number greater than 4
(vi) F : a number not less than 3.
Also, find A B, A B, E F, D E, A – C, D –
E, F′, E F′.
Answer:
(a) (i) A = {1, 2, 3, 4, 5, 6}
(ii) B=
(iii) C = {3, 6}
(iv) D = {1, 2, 3}
(v) E = {6}
(vi) F = {3, 4, 5, 6}.
(b) (i)A B = {1, 2, 3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6}
(ii) A B = {1, 2, 3, 4, 5, 6} =
(iii) E F = {6} {3, 4, 5, 6}
= {3, 4, 5, 6}
(iv) D E = {1, 2, 3} {6} =
(v) A – C = {1, 2, 3, 4, 5, 6} – {3, 6}
= {1, 2, 4, 5}
(vi) D – E = {1, 2, 3} – {6} = {1, 2, 3}
(vii) F′ = {1, 2, 3, 4, 5, 6} –
{3, 4, 5, 6} = {1, 2}
(viii) E F′ = {6} {1, 2} = .
Question 66:
An experiment involves rolling a pair of dice and
recording the numbers that come up.
Describe the following events :
- The sum is greater than 8
- 2 occurs on either die
- the sum is at least 7 and a multiple of 3.
Which pairs of these events are mutually exclusive ?
Answer:
A = {(3, 6), (6, 3), (4, 5), (5, 4), (4, 6),
(6, 4), (5, 5), (5, 6), (6, 5), (6, 6)}
B = {(1, 2), (2, 2), (3, 2), (4, 2), (5, 2),
(6, 2), (2, 1), (2, 3), (2, 4), (2, 5),
(2, 6)},
C = {(3, 6), (6, 3), (5, 4), (4, 5), (6, 6)}.
Now A B = , B C =
and A C = {(3, 6), (6, 3), (5, 4), (4, 5), (6, 6)}.
Hence A, B and B, C are mutually exclusive.
Question 67:
Three coins are tossed once. Let A denote the
event ‘‘Three heads show’’, B denote the event
‘‘two heads and one tail show’’, C denote the event
‘‘three tails show’’ and D denote the event ‘‘a head
shows on the first coin’’. Which events are :
mutually exclusive
Answer:
A = {HHH}
B = {HHT, HTH, THH}
C = {TTT}
D = {HHH, HHT, HTH, HTT}.
A and B, B and C, A and C, C and D are mutually
exclusive.
Question 68:
Three coins are tossed once. Let A denote the
event ‘‘Three heads show’’, B denote the event
‘‘two heads and one tail show’’, C denote the event
‘‘three tails show’’ and D denote the event ‘‘a head
shows on the first coin’’. Which events are :
simple
Answer:
A = {HHH}
B = {HHT, HTH, THH}
C = {TTT}
D = {HHH, HHT, HTH, HTT}.
A and C are simple events.
Question 69:
Three coins are tossed once. Let A denote the
event ‘‘Three heads show’’, B denote the event
‘‘two heads and one tail show’’, C denote the event
‘‘three tails show’’ and D denote the event ‘‘a head
shows on the first coin’’. Which events are :
compound
Answer:
A = {HHH}
B = {HHT, HTH, THH}
C = {TTT}
D = {HHH, HHT, HTH, HTT}.
B and D are compound events.
Question 70:
Three coins are tossed. Describe :
two events, which are mutually exclusive.
Answer:
‘‘Getting at least two heads’’ and ‘‘getting at least two tails.’’
Question 71:
Three coins are tossed. Describe :
three events, which are mutually exclusive and
exhaustive.
Answer:
‘‘Getting no heads’’, ‘‘getting exactly one head’’ and ‘‘getting at least two heads’’.
Question 72:
Three coins are tossed. Describe :
two events, which are not mutually exclusive.
Answer:
‘‘Getting at most two tails’’ and ‘‘getting exactly two tails’’.
Question 73:
Three coins are tossed. Describe :
two events, which are mutually exclusive but not
exhaustive.
Answer:
‘‘Getting exactly one head’’ and ‘‘getting exactly two heads’’.
Question 74:
Three coins are tossed. Describe :
three events, which are mutually exclusive but not
exhaustive.
Answer:
‘‘Getting exactly one tail’’, ‘‘getting exactly two tails’’ and ‘‘getting exactly three tails’’.
Question 75:
Two dice are thrown. The events A, B, C, D,
E, F are as follows :
A : getting an even number on the first die.
B : geting an odd number on the first die.
C : getting the sum of the numbers on the dice ≤ 5
Describe the events :
A′
Answer:
A = {(2, 1), (2, 2), (2, 3), (2, 4),
(2, 5), (2, 6),(4, 1), (4, 2),
(4, 3), (4, 4), (4, 5), (4, 6),
(6, 1), (6, 2), (6, 3), (6, 4),
(6, 5), (6, 6)}.
B = {(1, 1), (1, 2), (1, 3), (1, 4),
(1, 5), (1, 6), (3, 1) (3, 2),
(3, 3), (3, 4), (3, 5), (3, 6),
(5, 1), (5, 2), (5, 3), (5, 4),
(5, 5), (5, 6)}.
C = {(1, 1), (1, 2), (1, 3), (1, 4),
(2, 1), (2, 2), (2, 3), (3, 1),
(3, 2), (4, 1)}.
A′ = Getting an odd number on
the first die = B.
Question 76:
Two dice are thrown. The events A, B, C, D,
E, F are as follows :
A : getting an even number on the first die.
B : geting an odd number on the first die.
C : getting the sum of the numbers on the dice ≤ 5
Describe the events :
not B
Answer:
A = {(2, 1), (2, 2), (2, 3), (2, 4),
(2, 5), (2, 6),(4, 1), (4, 2),
(4, 3), (4, 4), (4, 5), (4, 6),
(6, 1), (6, 2), (6, 3), (6, 4),
(6, 5), (6, 6)}.
B = {(1, 1), (1, 2), (1, 3), (1, 4),
(1, 5), (1, 6), (3, 1) (3, 2),
(3, 3), (3, 4), (3, 5), (3, 6),
(5, 1), (5, 2), (5, 3), (5, 4),
(5, 5), (5, 6)}.
C = {(1, 1), (1, 2), (1, 3), (1, 4),
(2, 1), (2, 2), (2, 3), (3, 1),
(3, 2), (4, 1)}.
not B = Getting an even number on
the first die = A.
Question 77:
Two dice are thrown. The events A, B, C, D,
E, F are as follows :
A : getting an even number on the first die.
B : geting an odd number on the first die.
C : getting the sum of the numbers on the dice ≤ 5
Describe the events :
A or B
Answer:
A = {(2, 1), (2, 2), (2, 3), (2, 4),
(2, 5), (2, 6),(4, 1), (4, 2),
(4, 3), (4, 4), (4, 5), (4, 6),
(6, 1), (6, 2), (6, 3), (6, 4),
(6, 5), (6, 6)}.
B = {(1, 1), (1, 2), (1, 3), (1, 4),
(1, 5), (1, 6), (3, 1) (3, 2),
(3, 3), (3, 4), (3, 5), (3, 6),
(5, 1), (5, 2), (5, 3), (5, 4),
(5, 5), (5, 6)}.
C = {(1, 1), (1, 2), (1, 3), (1, 4),
(2, 1), (2, 2), (2, 3), (3, 1),
(3, 2), (4, 1)}.
A or B = A B
= {(1, 1), (1, 2), (1, 3), (1, 4),
(1, 5), (1, 6),(3, 1), (3, 2),
(3, 3), (3, 4), (3, 5), (3, 6),
(5, 1), (5, 2), (5, 3), (5, 4),
(5, 5), (5, 6), (2, 1), (2, 2),
(2, 3), (2, 4), (2, 5), (2, 6),
(4, 1) (4, 2), (4, 3), (4, 4),
(4, 5), (4, 6), (6, 1), (6, 2),
(6, 3), (6, 4), (6, 5), (6, 6)}
= S.
Question 78:
Two dice are thrown. The events A, B, C, D,
E, F are as follows :
A : getting an even number on the first die.
B : geting an odd number on the first die.
C : getting the sum of the numbers on the dice ≤ 5
Describe the events :
A and B
Answer:
A = {(2, 1), (2, 2), (2, 3), (2, 4),
(2, 5), (2, 6),(4, 1), (4, 2),
(4, 3), (4, 4), (4, 5), (4, 6),
(6, 1), (6, 2), (6, 3), (6, 4),
(6, 5), (6, 6)}.
B = {(1, 1), (1, 2), (1, 3), (1, 4),
(1, 5), (1, 6), (3, 1) (3, 2),
(3, 3), (3, 4), (3, 5), (3, 6),
(5, 1), (5, 2), (5, 3), (5, 4),
(5, 5), (5, 6)}.
C = {(1, 1), (1, 2), (1, 3), (1, 4),
(2, 1), (2, 2), (2, 3), (3, 1),
(3, 2), (4, 1)}.
A and B = A B = .
Question 79:
Two dice are thrown. The events A, B, C, D,
E, F are as follows :
A : getting an even number on the first die.
B : geting an odd number on the first die.
C : getting the sum of the numbers on the dice ≤ 5
Describe the events :
A but not C
Answer:
A = {(2, 1), (2, 2), (2, 3), (2, 4),
(2, 5), (2, 6),(4, 1), (4, 2),
(4, 3), (4, 4), (4, 5), (4, 6),
(6, 1), (6, 2), (6, 3), (6, 4),
(6, 5), (6, 6)}.
B = {(1, 1), (1, 2), (1, 3), (1, 4),
(1, 5), (1, 6), (3, 1) (3, 2),
(3, 3), (3, 4), (3, 5), (3, 6),
(5, 1), (5, 2), (5, 3), (5, 4),
(5, 5), (5, 6)}.
C = {(1, 1), (1, 2), (1, 3), (1, 4),
(2, 1), (2, 2), (2, 3), (3, 1),
(3, 2), (4, 1)}.
A but not C= {(2, 4), (2, 5), (2, 6), (4, 2),
(4, 3), (4, 4), (4, 5), (4, 6),
(6, 1), (6, 2), (6, 3), (6, 4),
(6, 5), (6, 6)}.
Question 80:
Two dice are thrown. The events A, B, C, D,
E, F are as follows :
A : getting an even number on the first die.
B : geting an odd number on the first die.
C : getting the sum of the numbers on the dice ≤ 5
Describe the events :
B or C
Answer:
A = {(2, 1), (2, 2), (2, 3), (2, 4),
(2, 5), (2, 6),(4, 1), (4, 2),
(4, 3), (4, 4), (4, 5), (4, 6),
(6, 1), (6, 2), (6, 3), (6, 4),
(6, 5), (6, 6)}.
B = {(1, 1), (1, 2), (1, 3), (1, 4),
(1, 5), (1, 6), (3, 1) (3, 2),
(3, 3), (3, 4), (3, 5), (3, 6),
(5, 1), (5, 2), (5, 3), (5, 4),
(5, 5), (5, 6)}.
C = {(1, 1), (1, 2), (1, 3), (1, 4),
(2, 1), (2, 2), (2, 3), (3, 1),
(3, 2), (4, 1)}.
B or C = B C = {(1, 1), (1, 2),
(1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (3, 1),
(3, 2), (3, 3), (3, 4), (3, 5),
(3, 6), (4, 1), (5, 1), (5, 2),
(5, 3), (5, 4), (5, 5)}.
Question 81:
Two dice are thrown. The events A, B, C, D,
E, F are as follows :
A : getting an even number on the first die.
B : geting an odd number on the first die.
C : getting the sum of the numbers on the dice ≤ 5
Describe the events :
B and C
Answer:
A = {(2, 1), (2, 2), (2, 3), (2, 4),
(2, 5), (2, 6),(4, 1), (4, 2),
(4, 3), (4, 4), (4, 5), (4, 6),
(6, 1), (6, 2), (6, 3), (6, 4),
(6, 5), (6, 6)}.
B = {(1, 1), (1, 2), (1, 3), (1, 4),
(1, 5), (1, 6), (3, 1) (3, 2),
(3, 3), (3, 4), (3, 5), (3, 6),
(5, 1), (5, 2), (5, 3), (5, 4),
(5, 5), (5, 6)}.
C = {(1, 1), (1, 2), (1, 3), (1, 4),
(2, 1), (2, 2), (2, 3), (3, 1),
(3, 2), (4, 1)}.
B C = {(1, 1), (1, 2), (1, 3), (1, 4),
(3, 1), (3, 2)}.
Question 82:
Two dice are thrown. The events A, B, C, D,
E, F are as follows :
A : getting an even number on the first die.
B : geting an odd number on the first die.
C : getting the sum of the numbers on the dice ≤ 5
Describe the events :
A B′ C′
Answer:
A = {(2, 1), (2, 2), (2, 3), (2, 4),
(2, 5), (2, 6),(4, 1), (4, 2),
(4, 3), (4, 4), (4, 5), (4, 6),
(6, 1), (6, 2), (6, 3), (6, 4),
(6, 5), (6, 6)}.
B = {(1, 1), (1, 2), (1, 3), (1, 4),
(1, 5), (1, 6), (3, 1) (3, 2),
(3, 3), (3, 4), (3, 5), (3, 6),
(5, 1), (5, 2), (5, 3), (5, 4),
(5, 5), (5, 6)}.
C = {(1, 1), (1, 2), (1, 3), (1, 4),
(2, 1), (2, 2), (2, 3), (3, 1),
(3, 2), (4, 1)}.
A B′ C′.
Here A = {(2, 1), (2, 2), (2, 3), (2, 4),
(2, 5), (2, 6), (4, 1), (4, 2),
(4, 3), (4, 4), (4, 5), (4, 6)
(6, 1), (6, 2), (6, 3), (6, 4),
(6, 5), (6, 6)}.
B′ = A.
and C′ = {(1, 5), (2, 4), (3, 3), (4, 2),
(5, 1), (1, 6), (2, 5), (3, 4)
(4, 3), (5, 2), (6, 1), (2, 6),
(3, 5), (4, 4), (5, 3), (6, 2),
(3, 6), (4, 5), (5, 4), (6, 3),
(4, 6), (5, 5), (6, 4), (5, 6),
(6, 5), (6, 6)}.
A B′ C′ = {(2, 4), (2, 5), (2, 6), (4, 2),
(4, 3), (4, 4), (4, 5), (4, 6),
(6, 1), (6, 2), (6, 3), (6, 4),
(6, 5), (6, 6)}.
Question 83:
Two dice are thrown. The events A, B and C are as
follows :
A : getting an even number on the first die
B : getting an odd number on the first die
C : getting the sum of numbers on the dice ≤ 5.
State true or false (give reasons for your answer) :
A and B are mutually exclusive
Answer:
True [Even and odd numbers cannot come on first die simultaneously]
Question 84:
Two dice are thrown. The events A, B and C are as
follows :
A : getting an even number on the first die
B : getting an odd number on the first die
C : getting the sum of numbers on the dice ≤ 5.
State true or false (give reasons for your answer) :
A and B are mutually exclusive and exhaustive
Answer:
True [Above reason along with the first die can have either even or odd number]
Question 85:
Two dice are thrown. The events A, B and C are as
follows :
A : getting an even number on the first die
B : getting an odd number on the first die
C : getting the sum of numbers on the dice ≤ 5.
State true or false (give reasons for your answer) :
A = B′
Answer:
True [Not B means B has even number on first die, which is same as A]
Question 86:
Two dice are thrown. The events A, B and C are as
follows :
A : getting an even number on the first die
B : getting an odd number on the first die
C : getting the sum of numbers on the dice ≤ 5.
State true or false (give reasons for your answer) :
A and C are mutually exclusive
Answer:
False [Sum can be ≤ 5 when first die shows even number, for ex. (2, 1) ; etc.]
Question 87:
Two dice are thrown. The events A, B and C are as
follows :
A : getting an even number on the first die
B : getting an odd number on the first die
C : getting the sum of numbers on the dice ≤ 5.
State true or false (give reasons for your answer) :
A and B′ are mutually exclusive
Answer:
False.
Question 88:
Two dice are thrown. The events A, B and C are as
follows :
A : getting an even number on the first die
B : getting an odd number on the first die
C : getting the sum of numbers on the dice ≤ 5.
State true or false (give reasons for your answer) :
A′, B′, C are mutually exclusive and exhaustive
Answer:
False.
Question 89:
Answer:
First Condition. Each p () is positive and
less than 1.
Second Condition. Sum of probabilities
= 0·1 + 0·01 + 0·05 + 0·03 + 0·01 + 0·2 + 0·6 = 1
Assignment is valid.
Question 90:
Answer:
Valid [Reasons as in part (a)]
Question 91:
Answer:
First Condition. Each p () is positive and less than 1.
Second Condition. Sum of probabilities.
= 0·1 + 0·2 + 0·3 + 0·4 + 0·5 + 0·6 + 0·7 > 1
Assignment is valid.
Question 92:
Answer:
First Condition. Each p () is not possible.
Assignment is valid.
Question 93:
Answer:
First Condition. Each assignment is not less than 1.
Assignment is valid.
Question 94:
A coin is tossed twice, what is the probability that at least one tail occurs ?
Answer:
Here Sample space,
S = {HH, HT, TH, TT},
where H Head and T Tail.
Let A be the event of getting at least one tail.
A = {HT, TH, TT}.
Question 95:
A die is thrown, find the probability of following events :
A prime number will appear
Answer:
Here n the number of exhaustive cases = 6.
Question 96:
A die is thrown, find the probability of following events :
A number greater than or equal to 3 will appear
Answer:
Here n the number of exhaustive cases = 6.
Question 97:
A die is thrown, find the probability of following events :
A number less than or equal to one will appear
Answer:
Here n the number of exhaustive cases = 6.
Question 98:
A die is thrown, find the probability of following events :
A number more than 0 will appear
Answer:
Here n the number of exhaustive cases = 6.
Question 99:
A die is thrown, find the probability of following events :
A number less than 6 will appear
Answer:
Here n the number of exhaustive cases = 6.
Question 100:
A card is selected from a pack of 52 cards.
How many points are there in the sample space ?
Answer:
Since there are 52 cards,
there are 52 points in the sample space.
Question 101:
A card is selected from a pack of 52 cards.
Calculate the probability that the card is an ace of
spades.
Answer:
Question 102:
A card is selected from a pack of 52 cards.
Calculate the probability that the card is :
(i) an ace (ii) black card.
Answer:
Question 103:
A fair coin with 1 marked on one face and 6 on the
other and a fair dice are both tossed. Find the probability
that the sum of the numbers that turn up is :
3
Answer:
No. of exhaustive cases = 2 × 6 = 12 No. of favourable cases = 1 [(1, 2)]
Question 104:
A fair coin with 1 marked on one face and 6 on the
other and a fair dice are both tossed. Find the probability
that the sum of the numbers that turn up is :
12
Answer:
No. of exhaustive cases = 2 × 6 = 12 No. of favourable cases = 1 [(6, 6)]
Question 105:
There are four men and six women on the city council. If one council member is selected for a committee at random, how likely is it that it is a woman.
Answer:
Any one person can be selected out of 10 (6W
+ 4M)
No. of exhaustive cases = 10.
One woman can be selected out of 6.
No. of favourable cases = 6
Question 106:
A fair coin is tossed four times and a person wins ` 1
for each head and loses ` 1·50 for each tail that turns up.
From the sample sapce, calculate how many different
amounts of money you can have after four tosses and the
probability of having each of these amounts ?
Answer:
Here S = {HHHH, HHHT, HHTH, HTHH,
THHH, HHTT, HTHT, HTTH, THHT, THTH, TTHH,
HTTT, THTT, TTHT, TTTH, TTTT}
Question 107:
Three coins are tossed once. Find the probability of getting :
3 heads
Answer:
Sample space, S = {HHH, HHT,
HTH, THH, HTT, THT, TTH, TTH}.
Question 108:
Three coins are tossed once. Find the probability of getting :
2 heads
Answer:
Sample space, S = {HHH, HHT,
HTH, THH, HTT, THT, TTH, TTH}.
Question 109:
Three coins are tossed once. Find the probability of getting :
at least 2 heads
Answer:
Sample space, S = {HHH, HHT,
HTH, THH, HTT, THT, TTH, TTH}.
Question 110:
Three coins are tossed once. Find the probability of getting :
at most 2 heads
Answer:
Sample space, S = {HHH, HHT,
HTH, THH, HTT, THT, TTH, TTH}.
Question 111:
Three coins are tossed once. Find the probability of getting :
no head
Answer:
Sample space, S = {HHH, HHT,
HTH, THH, HTT, THT, TTH, TTH}.
Question 112:
Three coins are tossed once. Find the probability of getting :
3 tails
Answer:
Sample space, S = {HHH, HHT,
HTH, THH, HTT, THT, TTH, TTH}.
Question 113:
Three coins are tossed once. Find the probability of getting :
exactly 2 tails
Answer:
Sample space, S = {HHH, HHT,
HTH, THH, HTT, THT, TTH, TTH}.
Question 114:
Three coins are tossed once. Find the probability of getting :
no tail
Answer:
Sample space, S = {HHH, HHT,
HTH, THH, HTT, THT, TTH, TTH}.
Question 115:
Three coins are tossed once. Find the probability of getting :
at most two tails
Answer:
Sample space, S = {HHH, HHT,
HTH, THH, HTT, THT, TTH, TTH}.
Question 116:
Answer:
Question 117:
A letter is chosen at random from the word
‘ASSASSINATION’. Find the probability that a
letter is :
a vowel
Answer:
The word ‘ASSASSINATION’ has 13 letters in
which 6 are vowels (viz. AAAIIO) and 7 consonants
(viz. SSSSNNT)
n (S) = 13.
No. of vowels = 6.
Question 118:
A letter is chosen at random from the word
‘ASSASSINATION’. Find the probability that a
letter is :
a consonant
Answer:
The word ‘ASSASSINATION’ has 13 letters in
which 6 are vowels (viz. AAAIIO) and 7 consonants
(viz. SSSSNNT)
n (S) = 13.
No. of consonants = 7.
Question 119:
In a lottery, a person chooses six different numbers at random from 1 to 20 and if these six numbers match with six numbers already fixed by the lottery committee, he wins the prize. What is the probability of winning the prize in the game ?
Answer:
Question 120:
Check whether the following probabilities P (A)
and P (B) are consistently defined :
P (A) = 0·5, P (B) = 0·7, P (A B) = 0·06
Answer:
P (A B) = P (A) + P (B) – P (A B)
= 0·5 + 0·7 – 0·06 = 1·20 – 0·06
= 1·14 > 1.
Hence the probabilities are not consistently defined.
Question 121:
Check whether the following probabilities P (A)
and P (B) are consistently defined :
P (A) = 0·5, P (B) = 0·4, P (A B) = 0·8
Answer:
P (A B) = P (A) + P (B) – P (A B)
0·8 = 0·5 + 0·4 – P (A B)
P (A B) = 0·9 – 0·8 = 0·1.
Hence the probabilities are consistently defined.
Question 122:
Answer:
Question 123:
Answer:
P (A B) = P (A) + P (B) – P (A B)
0·6 = 0·35 + P (B) – 0·25
P (B) = 0·6 – 0.1 = 0·5.
Question 124:
Answer:
P (A B) = P (A) + P (B) – P (A B)
0·7 = 0·5 + 0·35 – P (A B)
P (A B) = 0·35 + 0·5 – 0·7
= 0·35 – 0·2 = 0·15.
Question 125:
Answer:
Question 126:
P (E or F)
Answer:
Question 127:
P (not E and not F)
Answer:
Question 128:
Events E and F are such that P (not E or not F)
= 0·25. State whether E and F are mutually exclusive.
Answer:
Question 129:
A and B are two events such that :
P (A) = 0·42. P (B) = 0·48 and P (A and B) = 0·16.
Determine :
P (not A)
Answer:
P (not A) = 1 – P (A) = 1 – 0·42 = 0·58.
Question 130:
A and B are two events such that :
P (A) = 0·42. P (B) = 0·48 and P (A and B) = 0·16.
Determine :
P (not B)
Answer:
P (not B) = 1 – P (B) = 1 – 0·48 = 0·52.
Question 131:
A and B are two events such that :
P (A) = 0·42. P (B) = 0·48 and P (A and B) = 0·16.
Determine :
P (A or B)
Answer:
P (A or B) = P (A) + P (B) – P (A B)
= 0·42 + 0·48 – 0·16
= 0·90 – 0·16 = 0·74.
Question 132:
In class XI of a school 40% of the students study Mathematics and 30% study Biology. 10% of the class study both Mathematics and Biology. If a student is selected at random from the class, find the probability that he will be studying Mathematics or Biology.
Answer:
Question 133:
In an entrance test that is graded on the basis of two examinations, the probability of a randomly chosen student passing the first examination is 0·8 and the probability of passing the second examination is 6·7. The probability of passing at least one of them is 0·95. What is the probability of passing both ?
Answer:
Let A and B be two examinations.
Here P (A) = 0·8, P (B) = 0·7 and (P B) = 0·95.
P (A B) = P (A) + P (B) – P (A B)
0·95 = 0·8 + 0·7 – P (A B)
P(A B) = 1·5 – 0·95 = 0·55.
Hence P (Pasing both exam.) = 0·55.
Question 134:
The probability that a student will pass the final examination in both English and Hindi is 0·3 and the probability of passing neither is 0·1. If the probability of passing English examination is 0·75, what is the probability of passing the Hindi examination ?
Answer:
Let E and H be English and Hindi examination
respectively.
Here P (E H) = 0·5, 1 – P (E H) = 0·1
P (E H) = 0·9
and P (E) = 0·75.
NowP (E H) = P (E) + P (H) – P (E H)
0·9 = 0·75 + P (H) – 0·5
Hence P (H) = 1·4 – 0·75 = 0·65.
Question 135:
In a class of 60 students, 30 opted for NCC,
32 opted for NSS and 24 opted for both NCC and
NSS. If one of these students is selected at random,
find the probability that :
the student has opted for NCC or NSS
Answer:
Let A and B be two events when a student opts for NCC and NSS respectively.
Question 136:
In a class of 60 students, 30 opted for NCC, 32 opted for NSS and 24 opted for both NCC and NSS. If one of these students is selected at random, find the probability that :
the student has opted neither NCC nor NSSAnswer:
Let A and B be two events when a student opts for NCC and NSS respectively.
Question 137:
In a class of 60 students, 30 opted for NCC, 32 opted for NSS and 24 opted for both NCC and NSS. If one of these students is selected at random, find the probability that :
the student has opted NSS but not NCCAnswer:
Let A and B be two events when a student opts for NCC and NSS respectively.