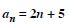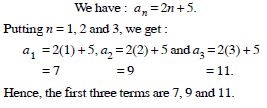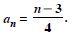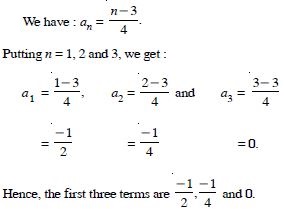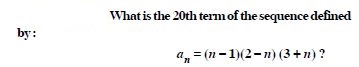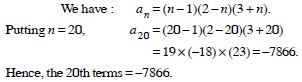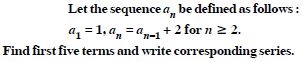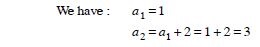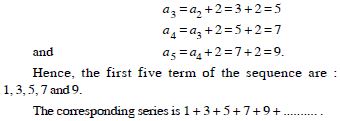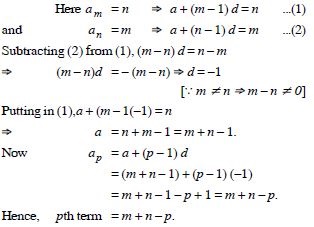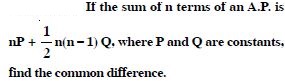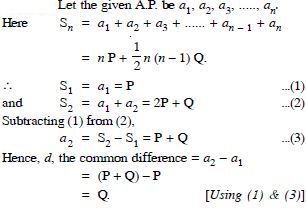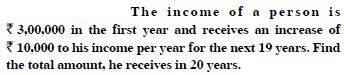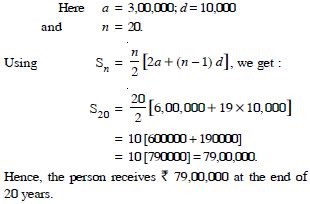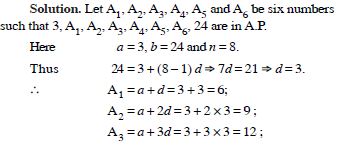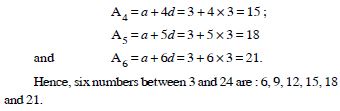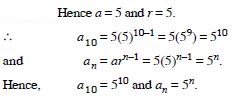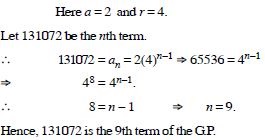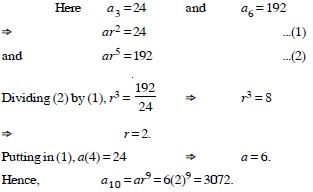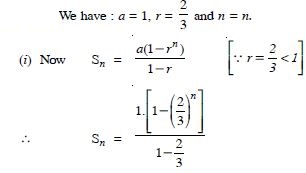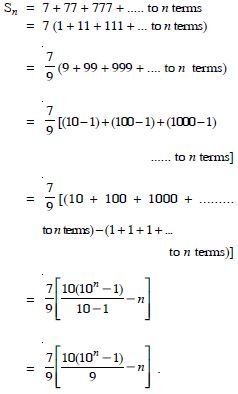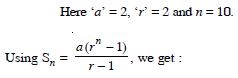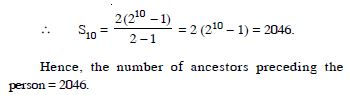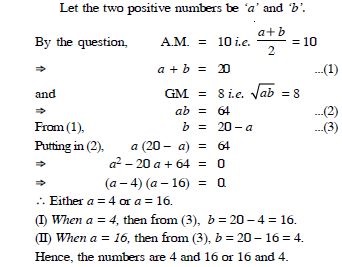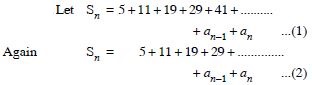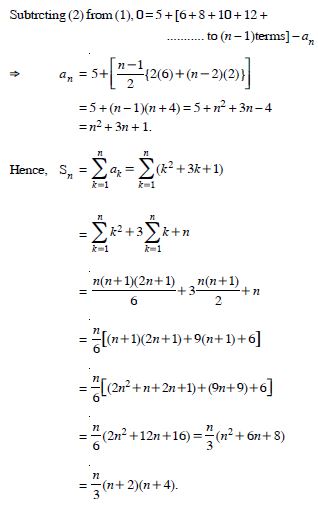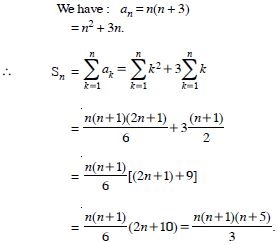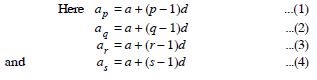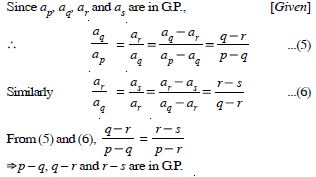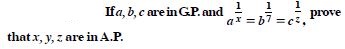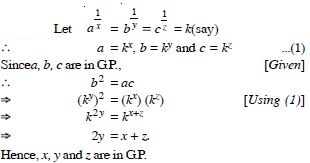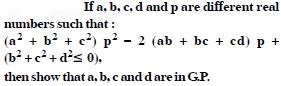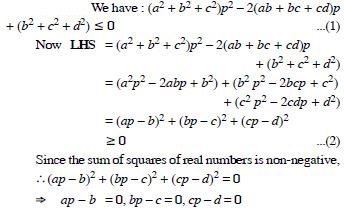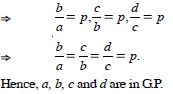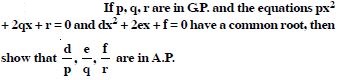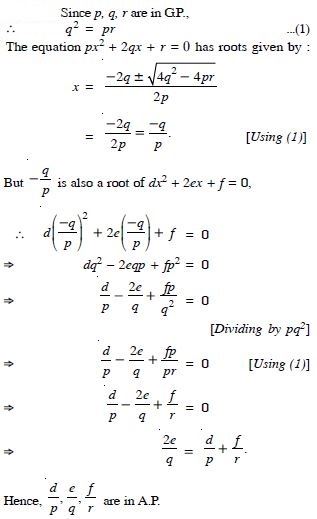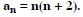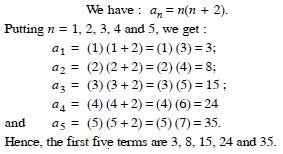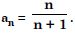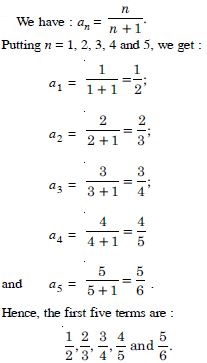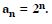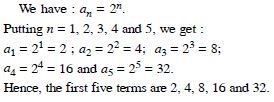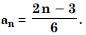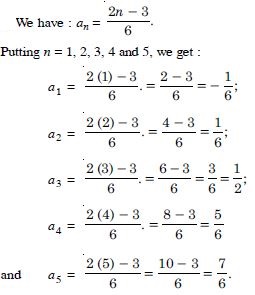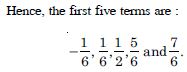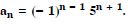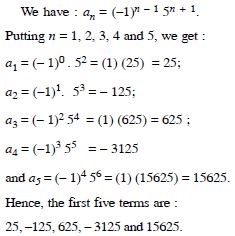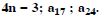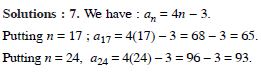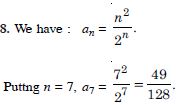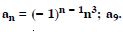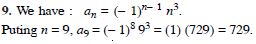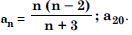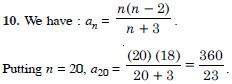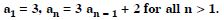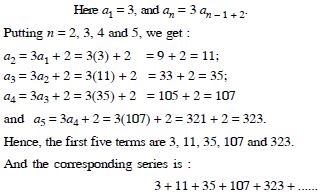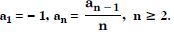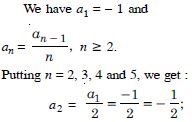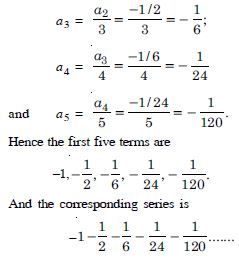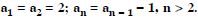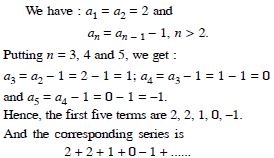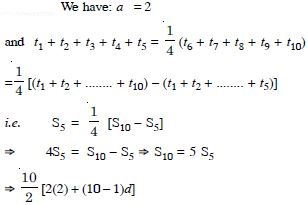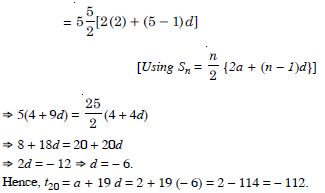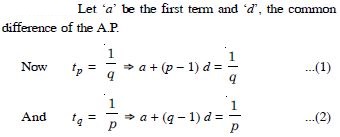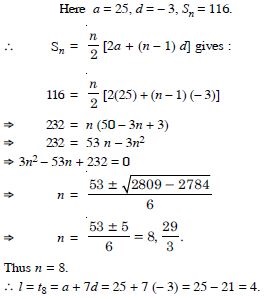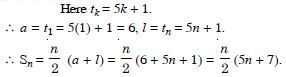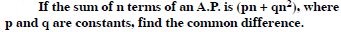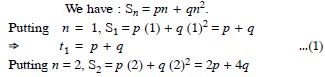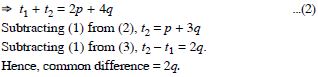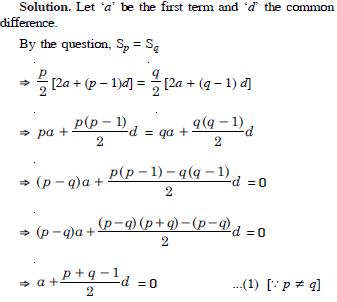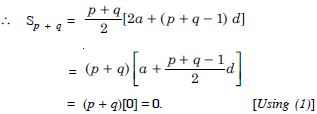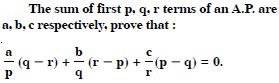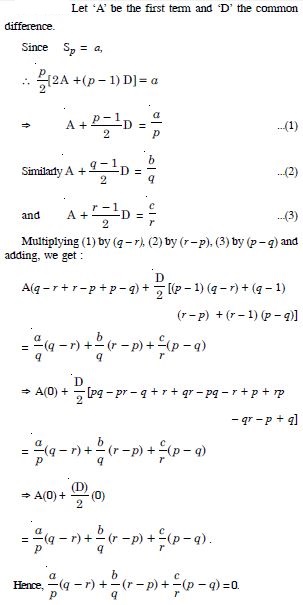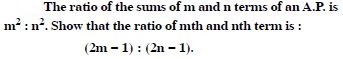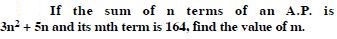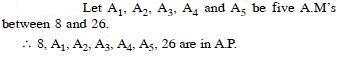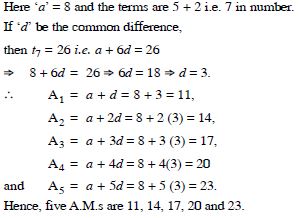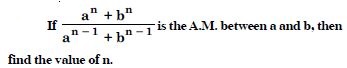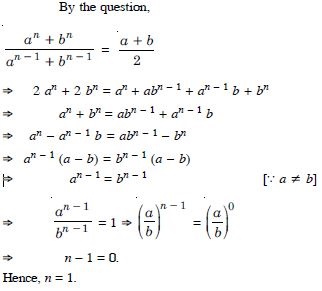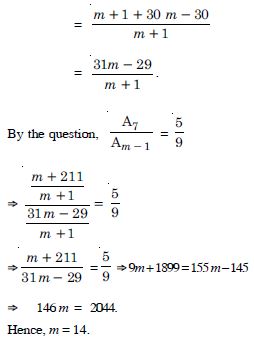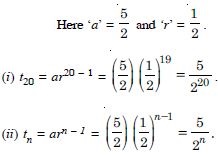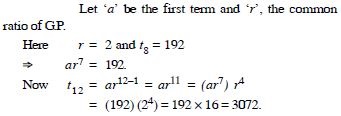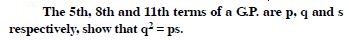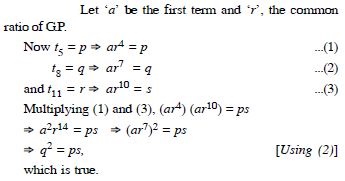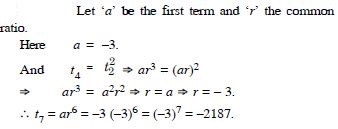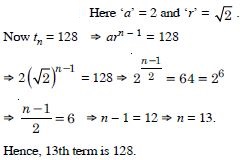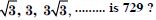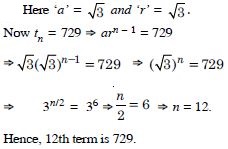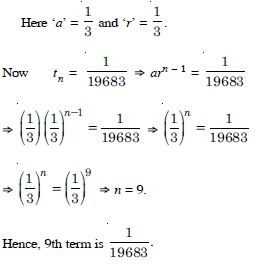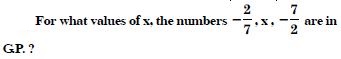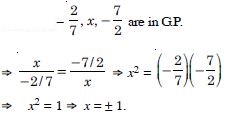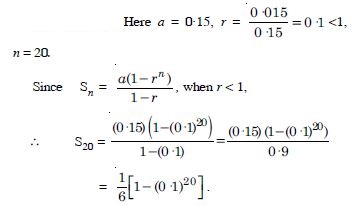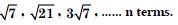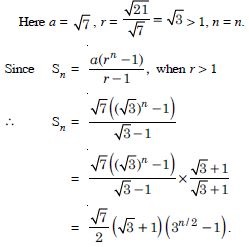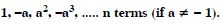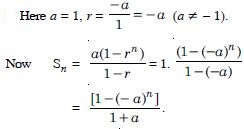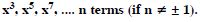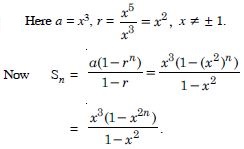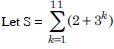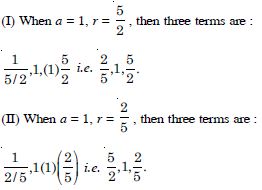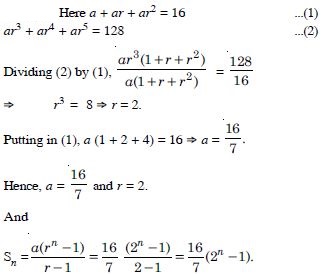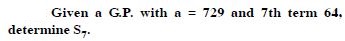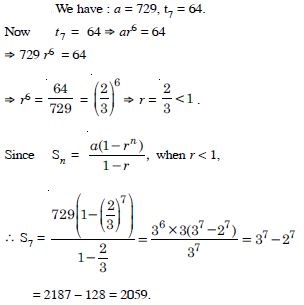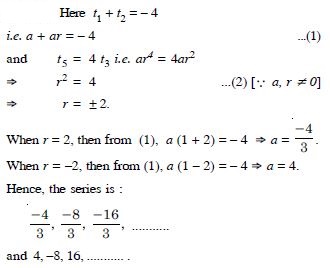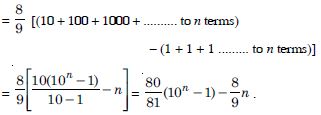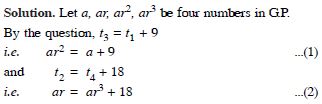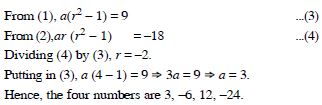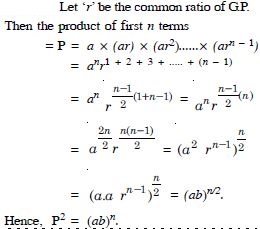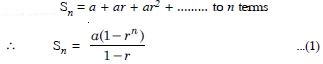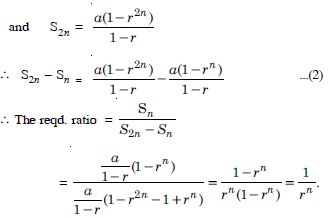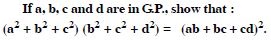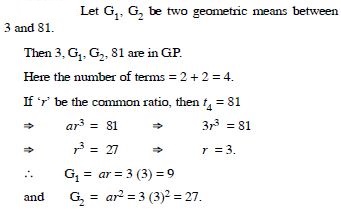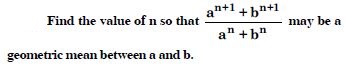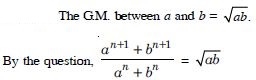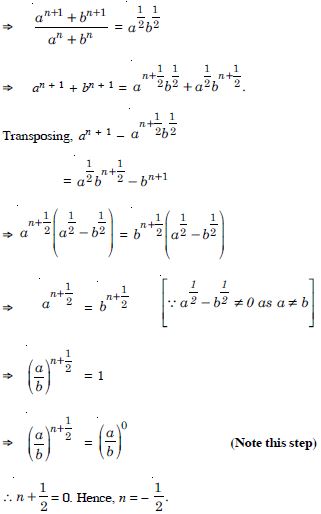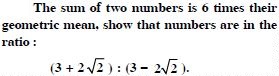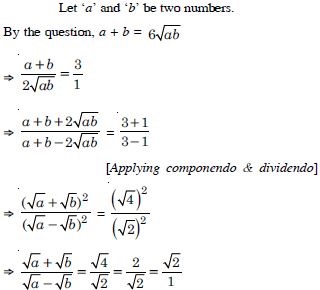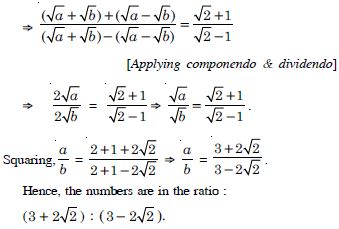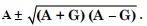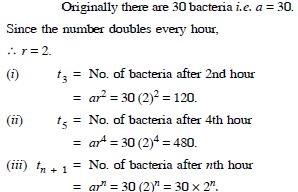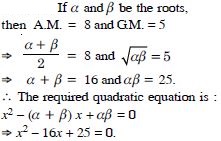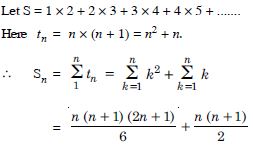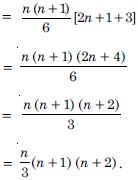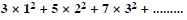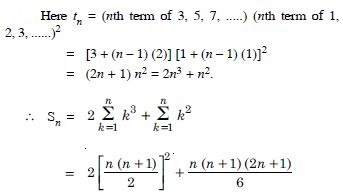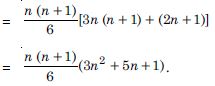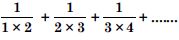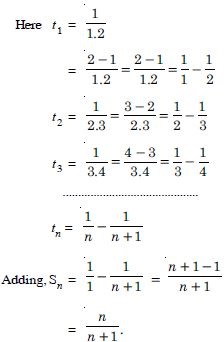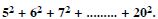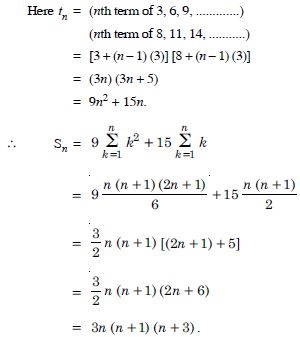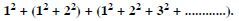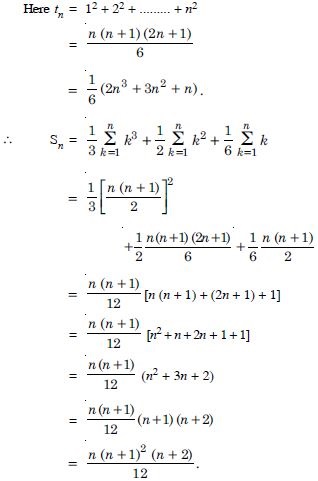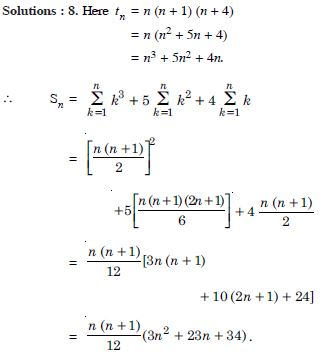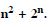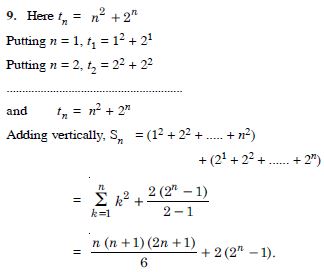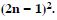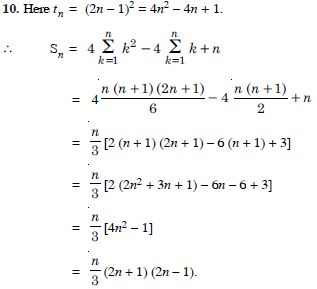NCERT Solutions for Class 11 Math Chapter 9 - Sequences and Series

Question 1:

Write the first three terms in each of the following sequences defined by the following :

Question 2:

Write the first three terms in each of the following sequences defined by the following :

Question 3:

Question 4:

Question 5:

In an A.P. if mth term is n and the nth term is m, where m $\ne$ n, find the pth term.

Question 6:

Question 7:

The sum of n term of two arithmetic progressions are in the ratio (3n + 8) : (7n + 15). Find the ratio of their 12th terms.

Question 8:

Question 9:

Question 10:

Insert 6 numbers between 3 and 24 such that the resulting sequence is an A.P.

Question 11:

Find the 10th and nth terms of the G.P.
5, 25, 125, …

Question 12:

Which term of the G.P. 2, 8, 32, .... upto n terms is 131072 ?

Question 13:

In a G.P., the 3rd term is 24 and the 6th term is 192. Find the 10th term.

Question 14:

Question 15:

Question 16:

Question 17:

Find the sum of the sequence :
7, 77, 777, 7777, ........ to n terms.

Question 18:

A person has 2 parents, 4 grand parents, 8 great–grand parents; and so on. Find the number of ancestors during the ten generations preceding his own.

Question 19:

Insert three numbers between the numbers 1 and 256 so that the resulting sequence is a G.P.

Question 20:

If A.M. and G.M. of two positive numbers a and b are 10 and 8 respectively , find the numbers.

Question 21:

Find the sum of n terms of the series :
5 + 11 + 19 + 29 + 41 + .................... .

Question 22:

Find the sum of n terms of the series whose nthe terms is n(n + 3).

Question 23:

If pth, qth, rth and sth terms of an A.P. are in G.P., then show that (p – q), (q – r), (r – s) are in G.P.

Question 24:

Question 25:

Question 26:

Question 27:

Write the first five terms of the sequence whose nth term is:

Question 28:

Write the first five terms of the sequence whose nth term is:

Question 29:

Write the first five terms of the sequence whose nth term is:

Question 30:

Write the first five terms of the sequence whose nth term is:

Question 31:

Write the first five terms of the sequence whose nth term is:

Question 32:

Write the first five terms of the sequence whose nth term is:

Question 33:

Find the indicated term in the sequence whose nth term is:

Question 34:

Find the indicated term in the sequence whose nth term is:

Question 35:

Find the indicated term in the sequence whose nth term is:

Question 36:

Find the indicated term in the sequence whose nth term is:

Question 37:

Write the first five terms of the sequences and obtain the corresponding series :

Question 38:

Write the first five terms of the sequences and obtain the corresponding series :

Question 39:

Write the first five terms of the sequences and obtain the corresponding series :

Question 40:

Question 41:

Find the sum of odd integers from 1 to 2001.

Question 42:

Find the sum of all natural numbers between 100 and 1000, which are multiples of 5.

Question 43:

In an A.P., the first term is 2 and the sum of first five terms is equal to one-fourth of the sum of the next five terms. Show that 20th term is – 112.

Question 44:

Question 45:

Question 46:

If the sum of a certain number of terms of the A.P.
25, 22, 19, ...... is 116, find the last term.

Question 47:

Find the sum of n terms of the A.P. whose kth term is 5k + 1.

Question 48:

Question 49:

The sum of n terms of two arithmetic progressions are in the ratio 5n + 4 : 9n + 6. Find the ratio of their 18th terms.

Question 50:

If the sum of first p terms of an A.P. is equal to the sum of the first q terms, then find the sum of the first (p + q) terms.

Question 51:

Question 52:

Question 53:

Question 54:

Insert five numbers between 8 and 26 such that the resulting sequence is an A.P.

Question 55:

Question 56:

Between 1 and 31, m arithmetic means have been inserted in such a way that the ratio of the 7th and (m – 1)th means is 5 : 9. Find the value of m.

Question 57:

Question 58:

The difference between any two consecutive interior angles of a polygon is 5$°$. If the smallest angle is 120$°$, find the number of sides of the polygon.

Question 59:

Question 60:

Find the 12th term of a G.P. whose 8th term is 192 and the common ratio is 2.

Question 61:

Question 62:

The fourth term of a G.P. is square of its 2nd term and the first term is –3. Determine the 7th term.

Question 63:

Which term of the following sequence :

Question 64:

Which term of the following sequence :

Question 65:

Which term of the following sequence :

Question 66:

Question 67:

Find the sum to indicated number of terms in the following geometric progressions:
0·15, 0·015, 0·0015, .... 20 terms.

Question 68:

Find the sum to indicated number of terms in the following geometric progressions:

Question 69:

Find the sum to indicated number of terms in the following geometric progressions:

Question 70:

Find the sum to indicated number of terms in the following geometric progressions:

Question 71:

Question 72:

Question 73:

Question 74:

The sum of first three terms of a G.P. is 16 and the sum of the next three terms is 128. Determine the first term, common ratio and the sum to n terms of the G.P.

Question 75:

Question 76:

Find a G.P. for which sum of first two terms is – 4 and the 5th term is 4 times the third term.

Question 77:

If the 4th, 10th and 16th terms of a G.P. are x, y, z respectively, prove that x, y, z are in G.P.

Question 78:

Find the sum to n terms of the sequence : 8, 88, 888, 8888, .....

Question 79:

Question 80:

Question 81:

Find four numbers forming a geometric progression in which the third term is greater than first by 9, and the second term is greater than the fourth by 18.

Question 82:

Question 83:

Question 84:

Question 85:

Question 86:

Insert two numbers between 3 and 81 so that the resulting sequence is in G.P.

Question 87:

Question 88:

Question 89:

If A and G be A.M. and G.M. respectively between two positive numbers, prove that the numbers are :

Question 90:

The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of 2nd hour, 4th hour and nth hour ?

Question 91:

If A.M. and G.M. of roots of a quadratic equation are 8 and 5 respectively, then obtain the quadratic equation.

Question 92:

Find the sum to n terms of each of the series in:
1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 + ........

Question 93:

Find the sum to n terms of each of the series in:
1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 + .......

Question 94:

Find the sum to n terms of each of the series in:

Question 95:

Find the sum to n terms of each of the series in:

Question 96:

Find the sum to n terms of each of the series in:

Question 97:

Find the sum to n terms of each of the series in:
3 × 8 + 6 × 11 + 9 × 14 + .........

Question 98:

Find the sum to n terms of each of the series in:

Question 99:

Find the sum to n terms of the series in whose nth term is given by :
n (n + 1) (n + 4) .

Question 100:

Find the sum to n terms of the series in whose nth term is given by :

Question 101:

Find the sum to n terms of the series in whose nth term is given by :