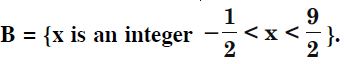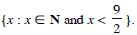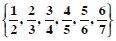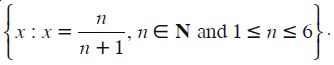Avail free NCERT Solutions online on Aasoka and study from the comfort of your home. Students can boost their learning efficiently with these solutions which are prepared by our subject matter experts. The NCERT Solutions for Class 11 focus on building a strong foundation for learning by providing questions and answers as per the latest CBSE syllabus. The entire chapter is covered properly in these solutions which can be utilized by the students to learn and score good marks in their exams.
In the “Sets” chapter of Maths Class 11 students will learn sets and their representation, how to draw Venn diagrams, the difference of sets, subsets, union and intersection of sets, power sets, equal sets, the complement of a set, empty set, subsets of the set of real number, universal set, finite and infinite sets, etc.
Question 1:
The collection of all months of a year beginning with letter J.
Answer:
Here the members of the collection are :
January, June and July.
Thus the collection is well defined and hence, it is a set.
Question 2:
The collection of ten most talented writers of India.
Answer:
The term ‘most talented’ is vague.
A writer is talented to a person and may not be so to the
other person.
Thus the collection is not well-defined and hence, it is not
a set.
Question 3:
A team of eleven best cricket batsmen of the world.
Answer:
The term ‘best’ is vague.
A batsman is best to one person and may not be so to the
other person.
Thus the collection is not well-defined and hence, it is not
a set.
Question 4:
The set of all boys in your class.
Answer:
Here the members of the collection are :
Boys in the class.
Thus the collection is well defined and hence, it is a set.
Question 5:
The collection of all natural numbers less than 100.
Answer:
Here the members of the collection are :
1, 2, 3, .............., , 97, 98, 99.
Thus the collection is well defined and hence, it is a set.
Question 6:
A collection of novels written by the writer Munshi Prem Chand.
Answer:
Members of the collection are :
Novels written by Munshi Prem Chand.
Thus the collection is well-defined and hence, it is a set.
Question 7:
The collection of all even integers.
Answer:
Members of the collection are :
2, 4, 6, ...............
Thus the collection is well-defined and hence, it is a set.
Question 8:
The collection of questions in this chapter.
Answer:
Members of the collection are :
Questions in this Chapter.
Thus the collection is well-defined and hence, it is a set.
Question 9:
A collection of most dangerous animals of the world.
Answer:
The term ‘most dangerous’ is vague.
An animal may be most dangerous to one person and may
not be so to the other person.
Thus the collection is not well defined and hence, it is not
a set.
Question 10:
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate
symbol or in the blank spaces.
5 ........ A
Answer:
5 A
Question 11:
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate
symbol or in the blank spaces.
8 .......... A
Answer:
8 A
Question 12:
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate
symbol or in the blank spaces.
0 .............. A
Answer:
0 A
Question 13:
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate
symbol or in the blank spaces.
4 ........ A
Answer:
4 A
Question 14:
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate
symbol or in the blank spaces.
2 .......... A
Answer:
2 A
Question 15:
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate
symbol or in the blank spaces.
10 .............. A
Answer:
10 A
Question 16:
Write the following sets in the roaster form :
A = {x : x is an integer and – 3 x < 7}.
Answer:
A = {– 3, – 2, – 1, 0, 1, 2, 3, 4, 5, 6}.
Question 17:
Write the following sets in the roaster form :
B = {x : x is a natural number less than 6}.
Answer:
B = {1, 2, 3, 4, 5}.
Question 18:
Write the following sets in the roaster form :
C = {x : x is a two-digit natural number such that
sum of its digits is 8}.
Answer:
C = {17, 26, 35, 44, 53, 62, 71, 80}.
Question 19:
Write the following sets in the roaster form :
D = {x : x is a prime number, which is a divisor
of 60}.
Answer:
D = {2, 3, 5}.
Question 20:
Write the following sets in the roaster form :
E = the set of all letters in the word
‘TRIGONOMETRY’.
Answer:
E = {T, R, I, G, O, N, M, E, Y}.
Question 21:
Write the following sets in the roaster form :
F = the set of all letters of the word ‘BETTER’.
Answer:
F = {B, E, T, R}.
Question 22:
List all the elements of the following sets :
A = {x : x is an odd natural number}.
Answer:
A = {1, 3, 5, 7, .........}.
Question 23:
List all the elements of the following sets :
Answer:
B = {0, 1, 2, 3, 4}.
Question 24:
List all the elements of the following sets :
C = {x : x is an integer, x2 4}.
Answer:
C = {– 2, – 1, 0, 1, 2}.
Question 25:
List all the elements of the following sets :
D = {x : x is a letter in the word ‘LOYAL’}.
Answer:
D = {L, O, Y, A}.
Question 26:
List all the elements of the following sets :
E = {x : x is a month of a year not having 31days}
Answer:
E ={February, April, June, September, November}.
Question 27:
List all the elements of the following sets :
F = {x : x is a consonant in the English alphabet word
which precedes k}.
Answer:
F = {b, c, d, f, g, h, j}.
Question 28:
Match each of the sets on the left in the roster form with the same set on the right described in the set builder form.
Answer:
(i)(c), (ii)(a), (iii)(d) (iv)(b).
Question 29:
Which of the following are examples of the null set ?
Set of odd natural numbers divisible by 2.
Answer:
[there is no odd natural number, which is divisible by 2]
Question 30:
Which of the following are examples of the null set ?
{x : x is a natural number, x < 5 and x> 7}.
Answer:
[there is no natural number, which is < 5 and> 7]
Question 31:
Which of the following are examples of the null set ?
{y : y is a point common to any two parallel lines}.
Answer:
[Parallel lines do not meet at a finite point].
Question 32:
Which of the following sets are finite or infinite ?
The set of months of a year
Answer:
Finite Set.
[ there are 12 months of a year]
Question 33:
Which of the following sets are finite or infinite ?
{1, 2, 3, .............}
Answer:
Infinite set.
[ there is infinite number of natural numbers]
Question 34:
Which of the following sets are finite or infinite ?
{1, 2, 3, ............, 99, 100}
Answer:
Finite Set.
[the set contains 100 natural numbers]
Question 35:
Which of the following sets are finite or infinite ?
The set of positive integers greater than 100
Answer:
Infinite set.
[there are infinite positive integers > 100]
Question 36:
Which of the following sets are finite or infinite ?
The set of prime numbers less than 99
Answer:
Finite Set.
[ the set is {2, 3, 5, ..............., 97}]
Question 37:
State whether each of the following sets is finite or infinite :
The set of lines, which are parallel to the x-axis.
Answer:
Infinite Set.
[ Infinite number of lines can be drawn
parallel to x-axis]
Question 38:
State whether each of the following sets is finite or infinite :
The set of letters in English alphabet.
Answer:
Finite Set.
[ This set contains 26 elements]
Question 39:
State whether each of the following sets is finite or infinite :
The set of numbers, which are multiples of 5.
Answer:
Infinite Set.
[ The set is {5, 10, 15, ........}]
Question 40:
State whether each of the following sets is finite or infinite :
The set of animals living on earth.
Answer:
Finite Set.
[ Finite number of animals live on earth]
Question 41:
State whether each of the following sets is finite or infinite :
The set of circles through origin (0, 0).
Answer:
Infinite Set.
[Infinite number of circles can be drawn passing
through the origin]
Question 42:
In the following, state whether A = B or not :
A = {a, b, c, d}, B = {d, c, b, a}.
Answer:
A = B
Question 43:
In the following, state whether A = B or not :
A = {4, 8, 12, 16}, B = {8, 4, 16, 18}.
Answer:
A B
Question 44:
In the following, state whether A = B or not :
A = {2, 4, 6, 8, 10},
B = {x : x is a positive even integer and x 10}
Answer:
A = B
Question 45:
In the following, state whether A = B or not :
A = {x : x is multiple of 10},
B = {10, 15, 20, 25, 30, .........}.
Answer:
A B
Question 46:
Are the following pair of sets equal ? Give reasons :
A = {2, 3}, B = {x : x is a solution of
x2 + 5x + 6 = 0}.
Answer:
Question 47:
Are the following pair of sets equal ? Give reasons :
A = {2, 3}, B = {x : x is a solution of
x2 + 5x + 6 = 0}.
Answer:
No.
x2 + 5x + 6 = 0 (x + 2) (x + 3) = 0
x = – 2, – 3.
Solution set is B = {– 2, – 3}.
But A = {2, 3}.
Hence, A B.
Question 48:
Are the following pair of sets equal ? Give reasons :
A = {x : x is a letter of the word FOLLOW},
B = {x : x is a letter of the word WOLF}.
Answer:
Yes.
A = {F, O, L, W} and
B = {W, O, L, F}.
Hence, A = B.
Question 49:
From the sets, given below, select examples of equal
sets :
A = {2, 4, 8, 12}, B = {1, 2, 3, 4},
C = {4, 8, 12, 14}, D = {3, 1, 4, 2},
E = {– 1, 1}, F = {0, 0},
G = {1, – 1}, H = {0, 1}.
Answer:
B = D and E = G.
Question 50:
Make correct statements by filling in the symbols
‘’ or ‘⊄’ in the blank spaces :
{2, 3, 4} ............... {1, 2, 3, 4, 5}
Answer:
Question 51:
Make correct statements by filling in the symbols
‘’ or ‘⊄’ in the blank spaces :
{a, b, c} ............... {b, c, d}
Answer:
⊄
Question 52:
Make correct statements by filling in the symbols
‘’ or ‘⊄’ in the blank spaces :
{x : x is a student of Class XI of your school}
........... {x : x is a student of your school}
Answer:
Question 53:
Make correct statements by filling in the symbols
‘’ or ‘⊄’ in the blank spaces :
{x : x is a circle in the plane} ............ {x : x is a
circle with radius 1}
Answer:
⊄
Question 54:
Make correct statements by filling in the symbols
‘’ or ‘⊄’ in the blank spaces :
{x : x is a triangle in the plane} ............. {x : x is
a rectangle in the plane}
Answer:
⊄
Question 55:
Make correct statements by filling in the symbols
‘’ or ‘⊄’ in the blank spaces :
{x : x is an equilateral triangle in the plane}...........
{x : x is a triangle in the plane}
Answer:
Question 56:
Make correct statements by filling in the symbols
‘’ or ‘⊄’ in the blank spaces :
{x : x is an even natural number}.......... {x : x is
an integer}.
Answer:
Question 57:
Examine whether the following statements are true
or false :
{a, b} ⊄ {b, c, a}
Answer:
False.
[Each element of {a, b} is in {b, c, a} {a, b}
{b, c, a}]
Question 58:
Examine whether the following statements are true
or false :
{a, e} {x : x is a vowel in the English alphabet}
Answer:
True.
[ a, e are vowels}
Question 59:
Examine whether the following statements are true
or false :
{1, 3, 5} {1, 3, 5}
Answer:
False.
[ {1, 3, 5} and {1, 3, 5} are equal sets
None is a proper subset of other]
Question 60:
Examine whether the following statements are true
or false :
{a} {a, b, c}
Answer:
True.
[a {a, b, c}]
Question 61:
Examine whether the following statements are true
or false :
{a} {a, b, c}
Answer:
False.
[ {a} {a, b, c}]
Question 62:
Examine whether the following statements are true
or false :
{x : x is an even natural number less than 6}
{x : x is a natural number which divides 36}
Answer:
True.
[ {x : x is an even natural number less than 6}
= {2, 4}
and {x : x is a natural number which divides 36}
= {1, 2, 3, 4, 6, 9, 12, 18, 36}
And as such {2, 4} {1, 2, 3, 4, 6, 9, 12, 18, 36}]
Question 63:
Let A = {1, 2, {3, 4}, 5}. Which of the following
statements are correct and why ?
{3, 4} A
Answer:
Incorrect
Question 64:
Let A = {1, 2, {3, 4}, 5}. Which of the following
statements are correct and why ?
{3, 4} A
Answer:
Correct
Question 65:
Let A = {1, 2, {3, 4}, 5}. Which of the following
statements are correct and why ?
3 A
Answer:
Correct
Question 66:
Let A = {1, 2, {3, 4}, 5}. Which of the following
statements are correct and why ?
1 A
Answer:
Correct
Question 67:
Let A = {1, 2, {3, 4}, 5}. Which of the following
statements are correct and why ?
1 A
Answer:
Incorrect
Question 68:
Let A = {1, 2, {3, 4}, 5}. Which of the following
statements are correct and why ?
{1, 2, 5} A
Answer:
Correct
Question 69:
Let A = {1, 2, {3, 4}, 5}. Which of the following
statements are correct and why ?
{1, 2, 5} A
Answer:
Incorrect
Question 70:
Let A = {1, 2, {3, 4}, 5}. Which of the following
statements are correct and why ?
{1, 2, 3} A
Answer:
Incorrect
Question 71:
Let A = {1, 2, {3, 4}, 5}. Which of the following
statements are correct and why ?
A
Answer:
Incorrect
Question 72:
Let A = {1, 2, {3, 4}, 5}. Which of the following
statements are correct and why ?
A
Answer:
Correct
Question 73:
Let A = {1, 2, {3, 4}, 5}. Which of the following
statements are correct and why ?
{} A
Answer:
Incorrect
Question 74:
Write down all the subsets of the following sets : {a}
Answer:
, {a}
Question 75:
Write down all the subsets of the following sets : {a, b}
Answer:
{a}, {b}, {a, b}
Question 76:
Write down all the subsets of the following sets : {1, 2, 3}
Answer:
, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, {1, 2, 3}
Question 77:
Write down all the subsets of the following sets :
Answer:
Question 78:
How many elements has P (A) if A = ?
Answer:
If A = .
Then by def., P (A) = P () = {}.
Hence, the set contains 1 element.
Question 79:
Write the following as intervals :
{x : x R, – 4 < x 6}
Answer:
(– 4, 6]
Question 80:
Write the following as intervals :
{x : x R, – 12 < x < – 10}
Answer:
(– 12, – 10)
Question 81:
Write the following as intervals :
{x : x R, 0 x < 7}
Answer:
[0, 7)
Question 82:
Write the following as intervals :
{x : x R, 3 x 4}
Answer:
[3, 4]
Question 83:
Write the following intervals in set-builder form : (– 3, 0)
Answer:
{x : x R, – 3 < x < 0}
Question 84:
Write the following intervals in set-builder form : [6, 12]
Answer:
{x : x R, 6 x 12}
Question 85:
Write the following intervals in set-builder form : (6, 12]
Answer:
{x : x R, 6 < x 12}
Question 86:
Write the following intervals in set-builder form : [– 23, 5)
Answer:
{x : x R, – 23 x < 5}
Question 87:
What universal set would you propose for each of the
following ?
(i) The set of right-triangles.
(ii) The set of isosceles triangles.
Answer:
(i) – (ii) Universal set is the set of all possible triangles for each of the given set.
Question 88:
Given the sets :
A = {1, 3, 5}, B = {2, 4, 6}, C = {0, 2, 4, 6, 8}.
Which of the following may be considered as universal
set(s) for all the three sets A, B and C ?
(i) {0, 1, 2, 3, 4, 5, 6}
(ii)
(iii) {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(iv) {1, 2, 3, 4, 5, 6, 7, 8}.
Answer:
The set (iii) {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} is the universal set for the sets A, B and C.
Question 89:
Find the union of each of the following pairs of sets : X = {1, 3, 5}, Y = {1, 2, 3}
Answer:
X Y
= {1, 3, 5} {1, 2, 3} = {1, 2, 3, 5}.
Question 90:
Find the union of each of the following pairs of sets :
A = {a, e, i, o, u}, B = {a, b, c}
Answer:
A B = {a, e, i, o, u} {a, b, c}
= {a, b, c, e, i, o, u}.
Question 91:
Find the union of each of the following pairs of sets :
A = {x : x is a natural number and multiple of 3},
B = {x : x is a natural number less than 6}
Answer:
A B = {3, 6, 9, .....} {1, 2, 3, 4, 5}
= {1, 2, 3, 4, 5, 6, 9, 12, .........}
Question 92:
Find the union of each of the following pairs of sets :
A = {x : x is a natural number and 1 < x 6}
B = {x : x is a natural number and 6 < x < 10}.
Answer:
A B = {2, 3, 4, 5, 6} {7, 8, 9}
= {2, 3, 4, 5, 6, 7, 8, 9}.
Question 93:
Find the union of each of the following pairs of sets :
A = {1, 2, 3}, B = .
Answer:
A B = A = {1, 2, 3}
= {1, 2, 3}.
Question 94:
Let A = {a, b} and B = {a, b, c}.
Is A B ? What is A B ?
Answer:
(i) A B [ each element of A is in B}
(ii) A B = {a, b} {a, b, c} = {a, b, c}.
Question 95:
If A and B are two sets such that A B, then what is A B ?
Answer:
Since A B each element of the set A is in the
set B.
A B = B.
Question 96:
A = {1, 2, 3, 4}, B = {3, 4, 5, 6},
C = {5, 6, 7, 8} and D = {7, 8, 9, 10}.
Find :A B
Answer:
A B = {1, 2, 3, 4} {3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6}.
Question 97:
A = {1, 2, 3, 4}, B = {3, 4, 5, 6},
C = {5, 6, 7, 8} and D = {7, 8, 9, 10}.
Find :A C
Answer:
A C = {1, 2, 3, 4} {5, 6, 7, 8}
= {1, 2, 3, 4, 5, 6, 7, 8}.
Question 98:
A = {1, 2, 3, 4}, B = {3, 4, 5, 6},
C = {5, 6, 7, 8} and D = {7, 8, 9, 10}.
Find : B C
Answer:
B C = {3, 4, 5, 6} {5, 6, 7, 8}
= {3, 4, 5, 6, 7, 8}.
Question 99:
A = {1, 2, 3, 4}, B = {3, 4, 5, 6},
C = {5, 6, 7, 8} and D = {7, 8, 9, 10}.
Find : B D
Answer:
B D = {3, 4, 5, 6} {7, 8, 9, 10}
= {3, 4, 5, 6, 7, 8, 9, 10}.
Question 100:
A = {1, 2, 3, 4}, B = {3, 4, 5, 6},
C = {5, 6, 7, 8} and D = {7, 8, 9, 10}.
Find : A B C
Answer:
A B C = {1, 2, 3, 4} {3, 4, 5, 6}
{5, 6, 7, 8}
= {1, 2, 3, 4, 5, 6} {5, 6, 7, 8}
= {1, 2, 3, 4, 5, 6, 7, 8}.
Question 101:
A = {1, 2, 3, 4}, B = {3, 4, 5, 6},
C = {5, 6, 7, 8} and D = {7, 8, 9, 10}.
Find : A B D
Answer:
A B D = {1, 2, 3, 4} {3, 4, 5, 6}
{7, 8, 9, 10}
= {1, 2, 3, 4, 5, 6} {7, 8, 9, 10}
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Question 102:
A = {1, 2, 3, 4}, B = {3, 4, 5, 6},
C = {5, 6, 7, 8} and D = {7, 8, 9, 10}.
Find : B C D
Answer:
B C D = {3, 4, 5} {5, 6, 7, 8}
{7, 8, 9, 10}
= {3, 4, 5, 6, 7, 8} {7, 8, 9, 10}
= {3, 4, 5, 6, 7, 8, 9, 10}.
Question 103:
Find the intersection of each pair of sets of question:
X = {1, 3, 5}, Y = {1, 2, 3}
Answer:
X Y = {1, 3, 5} {1, 2, 3} = {1, 3}.
Question 104:
Find the intersection of each pair of sets of question:
A = {a, e, i, o, u}, B = {a, b, c}
Answer:
A B = {a, e, i, o, u} {a, b, c} = {a}.
Question 105:
Find the intersection of each pair of sets of question:
A = {x : x is a natural number and multiple of 3},
B = {x : x is a natural number less than 6}
Answer:
A B = {3, 6, 9, .......} {1, 2, 3, 4, 5} = {3}.
Question 106:
Find the intersection of each pair of sets of question:
A = {x : x is a natural number and 1 < x ≤ 6}
B = {x : x is a natural number and 6 < x < 10}.
Answer:
A B = {2, 3, 4, 5, 6} {7, 8, 9} = .
Question 107:
Find the intersection of each pair of sets of question:
A = {1, 2, 3}, B = .
Answer:
A B = {1, 2, 3} = .
Question 108:
If A = {3, 5, 7, 9, 11} and
B = {7, 9, 11, 13},
C = {11, 13, 15}, D = {15, 17} ;
find : A B
Answer:
A B
= {3, 5, 7, 9, 11} {7, 9, 11, 13}
= {7, 9, 11}.
Question 109:
If A = {3, 5, 7, 9, 11} and
B = {7, 9, 11, 13},
C = {11, 13, 15}, D = {15, 17} ;
find : B C
Answer:
B C = {7, 9, 11, 13} {11, 13, 15}
= {11, 13}.
Question 110:
If A = {3, 5, 7, 9, 11} and
B = {7, 9, 11, 13},
C = {11, 13, 15}, D = {15, 17} ;
find : A C D
Answer:
A C D = {3, 5, 7, 9, 11} {11, 13, 15} {15, 17}
= {11} {15, 17} = .
Question 111:
If A = {3, 5, 7, 9, 11} and
B = {7, 9, 11, 13},
C = {11, 13, 15}, D = {15, 17} ;
find : A C
Answer:
A C = {3, 5, 7, 9, 11}
{11, 13, 15} = {11}.
Question 112:
If A = {3, 5, 7, 9, 11} and
B = {7, 9, 11, 13},
C = {11, 13, 15}, D = {15, 17} ;
find : B D
Answer:
B D = {7, 9, 11, 13} {15, 17} = .
Question 113:
If A = {3, 5, 7, 9, 11} and
B = {7, 9, 11, 13},
C = {11, 13, 15}, D = {15, 17} ;
find : A (B C)
Answer:
A (B C) = {3, 5, 7, 9, 11}
({7, 9, 11, 13} {11, 13, 15})
= {3, 5, 7, 9, 11} {7, 9, 11, 13, 15}
= {7, 9, 11}.
Question 114:
If A = {3, 5, 7, 9, 11} and
B = {7, 9, 11, 13},
C = {11, 13, 15}, D = {15, 17} ;
find : A D
Answer:
A D = {3, 5, 7, 9, 11} {15, 17} = .
Question 115:
If A = {3, 5, 7, 9, 11} and
B = {7, 9, 11, 13},
C = {11, 13, 15}, D = {15, 17} ;
find :A (B D)
Answer:
A (B D) = {3, 5, 7, 9, 11} ({7, 9, 11, 13}
{15, 17})
= {3, 5, 7, 9, 11}
{7, 9, 11, 13, 15, 17}
= {7, 9, 11}.
Question 116:
If A = {3, 5, 7, 9, 11} and
B = {7, 9, 11, 13},
C = {11, 13, 15}, D = {15, 17} ;
find :(A B) (B C)
Answer:
A B = {3, 5, 7, 9, 11}
{7, 9, 11, 13} = {7, 9, 11}
B C = {7, 9, 11, 13} {11, 13, 15}
= {7, 9, 11, 13, 15}.
(A B) (B C) = {7, 9, 11} {7, 9, 11, 13, 15}
= {7, 9, 11}.
Question 117:
If A = {3, 5, 7, 9, 11} and
B = {7, 9, 11, 13},
C = {11, 13, 15}, D = {15, 17} ;
find : (A D) (B C)
Answer:
A D = {3, 5, 7, 9, 11} {15, 17}
= {3, 5, 7, 9, 11, 15, 17}
B C = {7, 9, 11, 13}
{11, 13, 15}
= {7, 9, 11, 13, 15}.
(A D) (B C) = {3, 5, 7, 9, 11, 13, 15, 17}
{7, 9, 11, 13, 15}
= {7, 9, 11, 15}.
Question 118:
Let A = {x : x is a natural number},
B = {x : x is an even natural number},
C = {x : x is an odd natural number},
D = {x : x is a prime number}. Find :
A B
Answer:
Here A = {1, 2, 3, 4, .........},
B = {2, 4, 6, 8, .......},
C = {1, 3, 5, 7, .........},
and D = {2, 3, 5, 7, ...........}.
A B = {1, 2, 3, 4, .......}
{2, 4, 6, 8, .........}
= {2, 4, 6, 8, ........} = B.
Question 119:
Let A = {x : x is a natural number},
B = {x : x is an even natural number},
C = {x : x is an odd natural number},
D = {x : x is a prime number}. Find :
A C
Answer:
Here A = {1, 2, 3, 4, .........},
B = {2, 4, 6, 8, .......},
C = {1, 3, 5, 7, .........},
and D = {2, 3, 5, 7, ...........}.
A C = {1, 2, 3, 4, .........}
{1, 3, 5, 7, .........}
= {1, 3, 5, 7, .......} = C.
Question 120:
Let A = {x : x is a natural number},
B = {x : x is an even natural number},
C = {x : x is an odd natural number},
D = {x : x is a prime number}. Find :
A D
Answer:
Here A = {1, 2, 3, 4, .........},
B = {2, 4, 6, 8, .......},
C = {1, 3, 5, 7, .........},
and D = {2, 3, 5, 7, ...........}.
A D = {1, 2, 3, 4, .......}
{2, 3, 5, 7, 11, 13, .....}
= {2, 3, 5, 7, ........} = D.
Question 121:
Let A = {x : x is a natural number},
B = {x : x is an even natural number},
C = {x : x is an odd natural number},
D = {x : x is a prime number}. Find :
B C
Answer:
Here A = {1, 2, 3, 4, .........},
B = {2, 4, 6, 8, .......},
C = {1, 3, 5, 7, .........},
and D = {2, 3, 5, 7, ...........}.
B C = {2, 4, 6, 8, ......}
{1, 3, 5, 7, ......} = .
Question 122:
Let A = {x : x is a natural number},
B = {x : x is an even natural number},
C = {x : x is an odd natural number},
D = {x : x is a prime number}. Find :
B D
Answer:
Here A = {1, 2, 3, 4, .........},
B = {2, 4, 6, 8, .......},
C = {1, 3, 5, 7, .........},
and D = {2, 3, 5, 7, ...........}.
B D = {2, 4, 6, 8, ......}
{2, 3, 5, 7, ......} = {2}.
Question 123:
Let A = {x : x is a natural number},
B = {x : x is an even natural number},
C = {x : x is an odd natural number},
D = {x : x is a prime number}. Find :
C D
Answer:
Here A = {1, 2, 3, 4, .........},
B = {2, 4, 6, 8, .......},
C = {1, 3, 5, 7, .........},
and D = {2, 3, 5, 7, ...........}.
C D = {1, 3, 5, 7, .........}
{2, 3, 5, 7, ........} = {3, 5, 7, ......}.
= {x : x is an odd prime number}.
Question 124:
Which of the following pairs of sets are disjoint ?
{1, 2, 3, 4} and
{x : x is a natural number and 4 ≤ x ≤ 6}
Answer:
Not disjoint sets.
[ 4 is the common element]
Question 125:
Which of the following pairs of sets are disjoint ?
{a, e, i, o, u} and {c, d, e, f}
Answer:
Not-disjoint sets.
[e is the common element]
Question 126:
Which of the following pairs of sets are disjoint ?
{x : x is an even integer} and
{x : x is an odd integer}.
Answer:
Disjoint sets.
[ there is no common element]
Question 127:
Let A = {3, 6, 9, 12, 15, 18, 21},
B = {4, 8, 12, 16, 20},
C = {2, 4, 6, 8, 10, 12, 14, 16} and
D = {5, 10, 15, 20}.
Find : A – B
Answer:
A – B = {3, 6, 9, 12, 15, 18, 21}
– {4, 8, 12, 16, 20}
= {3, 6, 9, 15, 18, 21}.
Question 128:
Let A = {3, 6, 9, 12, 15, 18, 21},
B = {4, 8, 12, 16, 20},
C = {2, 4, 6, 8, 10, 12, 14, 16} and
D = {5, 10, 15, 20}.
Find :A – C
Answer:
A – C = {3, 6, 9, 12, 15, 18, 21}
– {2, 4, 6, 8, 10, 12, 14, 16}
= {3, 9, 15, 18, 21}.
Question 129:
Let A = {3, 6, 9, 12, 15, 18, 21},
B = {4, 8, 12, 16, 20},
C = {2, 4, 6, 8, 10, 12, 14, 16} and
D = {5, 10, 15, 20}.
Find : A – D
Answer:
A – D = {3, 6, 9, 12, 15, 18, 21} –
{5, 10, 15, 20}
= {3, 6, 9, 12, 18, 21}.
Question 130:
Let A = {3, 6, 9, 12, 15, 18, 21},
B = {4, 8, 12, 16, 20},
C = {2, 4, 6, 8, 10, 12, 14, 16} and
D = {5, 10, 15, 20}.
Find :B – A
Answer:
B – A = {4, 8, 12, 16, 20} –
{3, 6, 9, 12, 15, 18, 21}
= {4, 8, 16, 20}.
Question 131:
Let A = {3, 6, 9, 12, 15, 18, 21},
B = {4, 8, 12, 16, 20},
C = {2, 4, 6, 8, 10, 12, 14, 16} and
D = {5, 10, 15, 20}.
Find :C – A
Answer:
C – A = {2, 4, 6, 8, 10, 12, 14, 16}
– {3, 6, 9, 12, 15, 18, 21}
= {2, 4, 8, 10, 14, 16}.
Question 132:
Let A = {3, 6, 9, 12, 15, 18, 21},
B = {4, 8, 12, 16, 20},
C = {2, 4, 6, 8, 10, 12, 14, 16} and
D = {5, 10, 15, 20}.
Find :D – A
Answer:
D – A = {5, 10, 15, 20} –
{3, 6, 9, 12, 15, 18, 21}
= {5, 10, 20}.
Question 133:
Let A = {3, 6, 9, 12, 15, 18, 21},
B = {4, 8, 12, 16, 20},
C = {2, 4, 6, 8, 10, 12, 14, 16} and
D = {5, 10, 15, 20}.
Find :B – C
Answer:
B – C = {4, 8, 12, 16, 20}
– {2, 4, 6, 8, 10, 12, 14, 16}
= {20}.
Question 134:
Let A = {3, 6, 9, 12, 15, 18, 21},
B = {4, 8, 12, 16, 20},
C = {2, 4, 6, 8, 10, 12, 14, 16} and
D = {5, 10, 15, 20}.
Find :B – D
Answer:
B – D = {4, 8, 12, 16, 20}
– {5, 10, 15, 20}
= {4, 8, 12, 16}.
Question 135:
Let A = {3, 6, 9, 12, 15, 18, 21},
B = {4, 8, 12, 16, 20},
C = {2, 4, 6, 8, 10, 12, 14, 16} and
D = {5, 10, 15, 20}.
Find :C – B
Answer:
C – B = {2, 4, 6, 8, 10, 12, 14, 16}
– {4, 8, 12, 16, 20}
= {2, 6, 10, 14}.
Question 136:
Let A = {3, 6, 9, 12, 15, 18, 21},
B = {4, 8, 12, 16, 20},
C = {2, 4, 6, 8, 10, 12, 14, 16} and
D = {5, 10, 15, 20}.
Find :D – B
Answer:
D – B = {5, 10, 15, 20}
– {4, 8, 12, 16, 20}
= {5, 10, 15}.
Question 137:
Let A = {3, 6, 9, 12, 15, 18, 21},
B = {4, 8, 12, 16, 20},
C = {2, 4, 6, 8, 10, 12, 14, 16} and
D = {5, 10, 15, 20}.
Find :C – D
Answer:
C – D = {2, 4, 6, 8, 10, 12, 14, 16}
– {5, 10, 15, 20}
= {2, 4, 6, 8, 12, 14, 16}.
Question 138:
Let A = {3, 6, 9, 12, 15, 18, 21},
B = {4, 8, 12, 16, 20},
C = {2, 4, 6, 8, 10, 12, 14, 16} and
D = {5, 10, 15, 20}.
Find :D – C
Answer:
D – C = {5, 10, 15, 20}
– {2, 4, 6, 8, 10, 12, 14, 16}
= {5, 15, 20}.
Question 139:
If X = {a, b, c, d} and Y = {f, b, d, g}, find :
X – Y
Answer:
X – Y = {a, b, c, d} –
{f, b d, g} = {a, c}.
Question 140:
If X = {a, b, c, d} and Y = {f, b, d, g}, find :
Y – X
Answer:
Y – X = {f, b, d, g} – {a, b, c, d}
= {f, g}.
Question 141:
If X = {a, b, c, d} and Y = {f, b, d, g}, find :
X Y
Answer:
X Y = {a, b, c, d} {f, b, d, g} = {b, d}.
Question 142:
If R is the set of real numbers and Q is the set of rational numbers, then what is R – Q ?
Answer:
R – Q = (Set of real numbers)
– (Set of rational numbers)
= Set of irrational numbers.
Question 143:
State whether each of the following statement is
true or false. Justify your answer.
{2, 3, 4, 5} and {3, 6} are disjoint sets.
Answer:
False.
[3 is the common element]
Question 144:
State whether each of the following statement is
true or false. Justify your answer.
{a, e, i, o, u} and {a, b, c, d} are disjoint sets.
Answer:
False.
[a is the common element]
Question 145:
State whether each of the following statement is
true or false. Justify your answer.
{2, 6, 10, 14} and {3, 7, 11, 15} are disjoint sets.
Answer:
True.
[there is no common element]
Question 147:
State whether each of the following statement is
true or false. Justify your answer.
{2, 6, 10} and {3, 7, 11} are disjoint sets.
Answer:
True.
[that is no common element]
Question 148:
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9},
A = { 1, 2, 3, 4},
B = {2, 4, 6, 8}, C = {3, 4, 5, 6}.
Find : A′
Answer:
A′ = U – A
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 2, 3, 4}
= {5, 6, 7, 8, 9}.
Question 149:
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9},
A = { 1, 2, 3, 4},
B = {2, 4, 6, 8}, C = {3, 4, 5, 6}.
Find : B′
Answer:
B′ = U – B = {1, 2, 3, 4, 5, 6, 7, 8, 9}
– {2, 4, 6, 8}
= {1, 3, 5, 7, 9}.
Question 150:
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9},
A = { 1, 2, 3, 4},
B = {2, 4, 6, 8}, C = {3, 4, 5, 6}.
Find : (A C)′
Answer:
A C = {1, 2, 3, 4} {3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6}.
(A C)′ = U – (A C)
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 2, 3, 4, 5, 6}
= {7, 8, 9}.
Question 151:
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9},
A = { 1, 2, 3, 4},
B = {2, 4, 6, 8}, C = {3, 4, 5, 6}.
Find : (A B)′
Answer:
A B = {1, 2, 3, 4} {2, 4, 6, 8}
= {1, 2, 3, 4, 6, 8}.
(A B)′ = U – (A B)
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 2, 3, 4, 6, 8}
= {5, 7, 9}.
Question 152:
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9},
A = { 1, 2, 3, 4},
B = {2, 4, 6, 8}, C = {3, 4, 5, 6}.
Find : (A′)′
Answer:
(A′)′ = U – A′ = {1, 2, 3, 4, 5, 6, 7, 8, 9}
– {5, 6, 7, 8, 9} [Using part (i)]
= {1, 2, 3, 4}.
Question 153:
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9},
A = { 1, 2, 3, 4},
B = {2, 4, 6, 8}, C = {3, 4, 5, 6}.
Find : (B – C)′
Answer:
B – C = {2, 4, 6, 8} – {3, 4, 5, 6}
= {2, 8}.
(B – C)′ = U – (B – C)
= {1, 2, 3, ,4, 5, 6, 7, 8, 9} – {2, 8}
= {1, 3, 4, 5, 6, 7, 9}.
Question 154:
If U = {a, b, c, d, e, f, g, h}, find the complement of the
following sets :
A = {a, b, c}, B = {d, e, f, g}, C = {a, c, e, g}, D = {f, g, h, a}.
Answer:
(i) A′ = U – A
= {a, b, c, d, e, f, g, h} – {a, b, c}
= {d, e, f, g, h}.
(ii) B′ = U – B
= {a, b, c, d, e, f, g, h} – {d, e, f, g}
= {a, b, c, h}.
(iii) C′ = U – C
= {a, b, c, d, e, f, g, h} – {a, c, e, g}
= {b, d, f, h}.
(iv) D′ = U – D
= {a, b, c, d, e, f, g, h} – {f, g, h, a}
= {b, c, d, e}.
Question 155:
Taking the set of natural numbers as universal set,
write down the complements of the following sets :
{x : x is an even number}
Answer:
{x : x is an odd natural number}.
Question 156:
Taking the set of natural numbers as universal set,
write down the complements of the following sets :
{x : x is an odd number}
Answer:
{x : x is an even natural number}.
Question 157:
Taking the set of natural numbers as universal set,
write down the complements of the following sets :
{x : x is a positive multiple of 3}
Answer:
{x : x N and x is not a multiple of 3}.
Question 158:
Taking the set of natural numbers as universal set,
write down the complements of the following sets :
{x : x is a prime number}
Answer:
{x : x is a composite number and x = 1}.
Question 159:
Taking the set of natural numbers as universal set,
write down the complements of the following sets :
{x : x is a natural number divisible by 3 and 5}
Answer:
{x : x N and x is neither divisible by 3 nor by 5}.
Question 160:
Taking the set of natural numbers as universal set,
write down the complements of the following sets :
{x : x is a perfect square}
Answer:
{x : x N and x is not a perfect square}.
Question 161:
Taking the set of natural numbers as universal set,
write down the complements of the following sets :
{x : x is a perfect cube}
Answer:
{x : x N and x is not a perfect cube}.
Question 162:
Taking the set of natural numbers as universal set,
write down the complements of the following sets :
{x : x + 5 = 8}
Answer:
{x : x N and x ≠ 3}.
Question 163:
Taking the set of natural numbers as universal set,
write down the complements of the following sets :
{x : 2x + 5 = 9}
Answer:
{x : x N and x ≠ 2}.
Question 164:
Taking the set of natural numbers as universal set,
write down the complements of the following sets :
{x : x > 7}
Answer:
{x : x N and x < 7}.
Question 165:
Taking the set of natural numbers as universal set,
write down the complements of the following sets :
{x : x N and 2x + 1 > 10}
Answer:
Question 166:
If U = {1, 2, 3, 4, 5, 6, 7, 8, 9},
A = {2, 4, 6, 8},
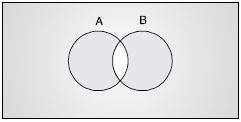
B = {2, 3, 5, 7}. Verify that :
(A B)′ = A′ B′
Answer:
A′ = U – A
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 4, 6, 8}
= {1, 3, 5, 7, 9}
and B′ = U – B
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 3, 5, 7}
= {1, 4, 6, 8, 9}.
A B = {2, 4, 6, 8} {1, 3, 5, 7}
= {1, 2, 3, 4, 5, 6, 7, 8}.
(A B)′ = U – (A B)
= {1, 2, 3, 4, 5, 6, 7, 8, 9}
– {1, 2, 3, 4, 5, 6, 7, 8}
= {9}.
And A′ B′ = {1, 3, 5, 7, 9} {1, 4, 6, 8, 9} = {9}.
Hence, (A B)′ = A′ B′.
Question 167:
If U = {1, 2, 3, 4, 5, 6, 7, 8, 9},
A = {2, 4, 6, 8},
B = {2, 3, 5, 7}. Verify that :
(A B)′ = A′ B′
Answer:
A′ = U – A
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 4, 6, 8}
= {1, 3, 5, 7, 9}
and B′ = U – B
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 3, 5, 7}
= {1, 4, 6, 8, 9}.
A B = {2, 4, 6, 8} {2, 3, 5, 7}
= {2}
(A B)′ = U – (A B)
= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2}
= {1, 3, 4, 5, 6, 7, 8, 9}.
And A′ B′= {1, 3, 5, 7, 9} {1, 4, 6, 8, 9}
= {1, 3, 4, 5, 6, 7, 8, 9}.
Hence, (A B)′ = A′ B′.
Question 168:
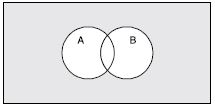
Draw appropriate Venn diagram for each of the following :
(A B)′
Answer:
(A B)′ is shown as shaded in the following figure :
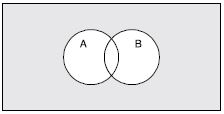
Question 169:
Draw appropriate Venn diagram for each of the following :
A′ B′
Answer:
A′ B′ is shown shaded in the following figure :
Question 170:
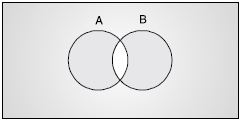
Draw appropriate Venn diagram for each of the following :
(A B)′
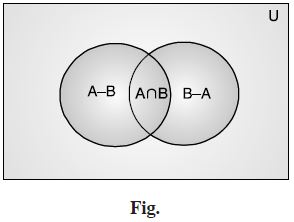
Answer:
(A B)′ is shown as shaded in the following figure :
Question 171:
Draw appropriate Venn diagram for each of the following :
A′ B′
Answer:
A′ B′ is shown as shaded in the following figure :
Question 172:
Let U be the set of all triangles in a plane. If A is the set of all triangles with at least one angle different from 60°, what is A′ ?
Answer:
We have A : Set of triangles in which no triangle
is equilateral.
A′ : Set of equilateral triangles.
Question 173:
Fill in the blanks to make each of the following a true statement :
A A′ = .........
Answer:
Let U be the universal set.
A A′ = U
Question 174:
Fill in the blanks to make each of the following a true statement :
′ A = .........
Answer:
Let U be the universal set.
′ A = U A = A
Question 175:
Fill in the blanks to make each of the following a true statement :
A A′ = .........
Answer:
Let U be the universal set.
A A′ =
Question 176:
Fill in the blanks to make each of the following a true statement :
U′ A = .........
Answer:
Let U be the universal set.
U′ A = A =
Question 177:
If X, Y are two sets such that :
n (X) = 17, n (Y) = 23 and n (X Y) = 38,
find n (X Y).
Answer:
n (X Y)
= n (X) + n (Y) – n (X Y)
38 = 17 + 23 – n (X Y)
n (X Y) = 40 – 38 = 2.
Question 178:
If X and Y are two sets such that X Y has 18 elements, X has 8 elements and Y has 15 elements, how many elements does X Y have ?
Answer:
We have : n (X Y) = 18, n (X) = 8
and n (Y) = 15.
Now n (X Y)
= n (X) + n (Y) – n (X Y)
18 = 8 + 15 – n (X Y)
n (X Y) = 23 – 18 = 5.
Question 179:
In a group of 400 people, 250 can speak Hindi and 200 can speak English. How many people can speak both Hindi and English ?
Answer:
Let
H = Set of people who can speak Hindi
and E = Set of people who can speak English.
By the question,
n (H) = 250, n (E) = 200 and n (H E) = 400.
Now n (H E) = n (H) + n (E) – n (H E)
400 = 250 + 200 – n ( H E)
n (H E) = 450 – 400 = 50.
Hence, 50 can speak both Hindi and English.
Question 180:
If S and T are two sets such that S has 21 elements, T has 32 elements and S T has 11 elements, how many elements does S T have ?
Answer:
We have : n (S) = 21, n (T) = 32, n (S T) = 11.
Now n (S T) = n (S) + n (T) – n (S T)
= 21 + 32 – 11
= 53 – 11 = 42.
Hence, S T has 42 elements.
Question 181:
If X and Y are two sets such that X has 40 elements, X Y has 60 elements and X Y has 10 elements, how many elements does Y have ?
Answer:
We have :
n (X) = 40, n (X Y) = 60, n (X Y) = 10.
Now n (X Y) = n (X) + n (Y) – n (X Y)
60 = 40 + n (Y) – 10
n (Y) = 60 – 40 + 10 = 30.
Hence, Y has 30 elements.
Question 182:
In a group of 70 people, 37 like coffee, 52 like tea and each person likes atleast one of the two drinks. How many like both coffee and tea ?
Answer:
Let C = Set of people who like coffee
and T = Set of people who like tea.
By the question, n (C T) = 70, n (C) = 37, n (T) = 52.
Now n (C T) = n (C) + n (T) – n (C T)
70 = 37 + 52 – n (C T)
n (C T) = 89 – 70 = 19.
Hence, 19 people like both coffee and tea.
Question 183:
In a group of 65 people, 40 like cricket, 10 like both cricket and tennis. How many like tennis only and not cricket ? How many like tennis ?
Answer:
Let C = Set of people who like cricket
and T = Set of people who like tennis.
By the question,
n (C T) = 65, n (C) = 40, n (C T) = 10.
Now n (C T) = n (C) + n (T) – n (C T)
65 = 40 + n (T) – 10
n (T) = 65 – 40 + 10 = 35.
Number of people who like only tennis
= n (T) – n (C T)
= 35 – 10 = 25.
Hence, 25 people like tennis only and not Cricket and
35 people like tennis.
Question 184:
In a committee 50 people speak French, 20 speak Spanish and 10 speak both Spanish and French. How many speak atleast one of these two languages ?
Answer:
Let F = Set of people who speak French
and S = Set of people who speak Spanish.
By the question, n (F) = 50, n (S) = 20,
n (F S) = 10.
Now n (F S) = n (F) + n (S) – n (F S)
= 50 + 20 – 10 = 60.
Hence, 60 people speak at least one of the two languages.
Question 185:
Write the solution set of the equation :
x2 + x – 2 = 0
in roster form.
Answer:
The given equation is x2 + x – 2 = 0
(x + 2) (x – 1) = 0 x = – 2, 1.
Hence, the required solution set = {– 2, 1}.
Question 186:
Write the set {x : x is a positive integer and x2 < 40} in the roster form.
Answer:
The squares of positive integers whose squares
are less than 40 are 1, 2, 3, 4, 5, 6.
Hence, the given set, in roster form, is :
{1, 2, 3, 4, 5, 6}.
Question 187:
Write the set {1, 4, 9, 16, 25, ....} in the set builder form.
Answer:
The elements of the given set are squares of
integers :
1, 2, 3, 4, 5, ......
Hence, the given set, in the set builder form, is :
{x : x = n2, where n N}.
Question 188:
Write the set
in the set builder form.
Answer:
In each element of the given set, the denominator is one more than the numerator. Also the numerators are from 1 to 6. Hence, the set builder form of the given set is :
Question 189:
Which of the following sets are finite and infinite :
{x : x N and (x – 1)(x – 2) = 0}
Answer:
Since (x – 1)(x – 2) = 0 x = 1, 2,
both N.
Hence, the given set = {1, 2}, which is finite.
Question 190:
Which of the following sets are finite and infinite :
{x : x N and x2 = 4}
Answer:
Here x2 = 4 x = 2.
But 2 N.
Hence, the given set = {2}, which is finite.
Question 191:
Which of the following sets are finite and infinite :
{x : x N and 2x – 1 = 0}
Answer:
Here 2x – 1 = 0 2x = 1
Hence, the given set = , which is finite.
Question 192:
Which of the following sets are finite and infinite :
{x : x N and x is prime}
Answer:
Since the set of prime natural numbers is infinite,
the given set is infinite.
Question 193:
Which of the following sets are finite and infinite :
{x : x N and x is odd}.
Answer:
Since there are infinite number of odd natural numbers,
the given set is infinite.
Question 194:
Find the pairs of equal sets from the
following sets, if any, giving reasons :
A = {0}, B = {x : x > 15 and x < 5},
C = {x : x – 5 = 0}, D = {x : x2 = 25},
E = {x : x is an integral positive root of
the equation x2 – 2x – 15 = 0}.
Answer:
Here we have :
A = {0}
B = [ There is no number, which is
greater than 15 and less than 5]
C = {5} [ x – 5 = 0 x = 5]
D = {–5, 5} [ x2 = 25 x = 5]
and E = {5}. [x2 – 2x – 15 = 0
(x – 5) (x + 3) = 0
x = 5, – 3. Out of these two, 5 is positive integer]
Clearly C = E.
Question 195:
Which of the following pairs of sets are
equal ? Justifiy your answer.
X, the set of letters in ‘ALLOY’ and
B, the set of letters in ‘LOYAL’
Answer:
Yes. [ X = B = {L, O, Y, A, L}]
Question 196:
Which of the following pairs of sets are
equal ? Justifiy your answer.
A = {n : n Z and n2 ≤ 4} and
B = {x : x R and x2 – 3x + 2 = 0}.
Answer:
No. [ A = {–2, –1, 0, 1, 2}
and B = {1, 2} because (x – 1)
(x – 2) = 0 x = 1, 2]
Question 197:
Consider the following sets :
, A = {1, 3}, B = {1, 5, 9}, C = {1, 3, 5, 7, 9}.
Insert the correct symbol or ⊄ between each pair
of sets :
.......B
Answer:
B [ is a subset of every set]
Question 198:
Consider the following sets :
, A = {1, 3}, B = {1, 5, 9}, C = {1, 3, 5, 7, 9}.
Insert the correct symbol or ⊄ between each pair
of sets :
A.........B
Answer:
A ⊄ B [ 3 A but 3 B]
Question 199:
Consider the following sets :
, A = {1, 3}, B = {1, 5, 9}, C = {1, 3, 5, 7, 9}.
Insert the correct symbol or ⊄ between each pair
of sets :
A..........C
Answer:
A C [ 1, 3 both A and C]
Question 200:
Consider the following sets :
, A = {1, 3}, B = {1, 5, 9}, C = {1, 3, 5, 7, 9}.
Insert the correct symbol or ⊄ between each pair
of sets :
B..........C
Answer:
B C. [ 1, 5, 9 all B and C]
Question 201:
Let A = {a, e, i, o, u} and B = {a, b, c, d}.
Is A a subset of B ? Is B a subset of A ?
Answer:
(i) No. A is not a subset of B.
[ e, i, o, u B]
(ii) No. B is not a subset of A. [ b, c, d A]
Question 202:
Let A, B and C be three sets. If A B and B C, is it true that A C ? If not, give an example.
Answer:
The given statement is not true.
Let A = {p}, B = C = {p}, {q}.
Here A B and B C [ B = C B C]
and A ⊄ C. [ p A but p C]
Question 203:
Let A = {2, 4, 6, 8} and B = {6, 8, 10, 12}.
Find A B.
Answer:
A B = {2, 4, 6, 8} {6, 8, 10, 12}
= {2, 4, 6, 8, 10, 12}.
Question 204:
Let A = {a, e, i, o, u} and B = {a, i, u}.
Show that A B = A.
Answer:
A B = {a, e, i, o, u} {a, i, u}
= {a, e, i, o, u} = A.
Question 205:
Let X = {Ram, Geeta, Akbar} be the set of students of Class XI, who are in school hockey team. Let Y = {Geeta, David, Ashok} be the set of students from class XI who are in school football team. Find XY and interpret the set.
Answer:
X Y = {Ram, Geeta, Akbar} {Geeta,
David, Ashok}
= {Ram, Geeta, Akbar, David,
Ashok},
which is a set of students from class XI who are in the
hockey team or the football team or both.
Question 206:
Let A = {2, 4, 6, 8} and B = {6, 8, 10, 12}. Find A B.
Answer:
A B = {2, 4, 6, 8} {6, 8, 10, 12}
= {6, 8}.
Question 207:
Let X = {Ram, Geeta, Akbar} be the set of students of Class XI, who are in school hockey team. Let Y = {Geeta, David, Ashok} be the set of students from class XI who are in school football team. Find X Y.
Answer:
X Y = {Ram, Geeta, Akbar} {Geeta,
David, Ashok}
= {Geeta}.
Question 208:
Let A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and
B = {2, 3, 5, 7}. Find A B and hence show that A B = B.
Answer:
A B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
{2, 3, 5, 7}
= {2, 3, 5, 7} = B.
Question 209:
Let A = {1, 2, 3, 4, 5, 6}, B = {2, 4, 6, 8}.
Find A–B and B–A.
Answer:
A – B = {1, 2, 3, 4, 5, 6} – {2, 4, 6, 8}
= {1, 3, 5}.
B – A = {2, 4, 6, 8} – {1, 2, 3, 4, 5, 6}
= {8}.
Question 210:
Let V = {a, e, i, o, u} and B = {a, i, k, u}.
Find V – B and B – V.
Answer:
V – B = {a, e, i, o, u} – {a, i, k, u}
= {e, o}
and B – V = {a, i, k, u} – {a, e, i, o, u} = {k}.
Question 211:
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and
A = {1, 3, 5, 7, 9}. Find A′.
Answer:
A′ = Set of those elements of U,
which are not in A
= {2, 4, 6, 8, 10}.
Question 212:
Let U be universal set of all students of class XI of a co-educational school and A be the set of girls in class XI. Find A′.
Answer:
A′ = Set of those elements of U,
which are not in A
= Set of all boys in class XI.
Question 213:
Let U = {1, 2, 3, 4, 5, 6}, A = {2, 3}
and B = {3, 4, 5}. Find A′, B′, A′ B′, A B and
hence show that (A B)′ = A′ B′.
Answer:
Here U = {1, 2, 3, 4, 5, 6}, A = {2, 3} and
B = {3, 4, 5}.
(i) A′ = Set of those elements of U, which are not in
A = {1, 4, 5, 6}.
(ii) B′ = Set of those elements of U, which are not in
B = {1, 2, 6}.
(iii) A′ B′ = {1, 4, 5, 6} {1, 2, 6} = {1, 6}.
(iv) A B = {2, 3} {3, 4, 5} = {2, 3, 4, 5}.
(v) (A B)′ = Set of those elements of U,
which are not in (A B)
= {1, 6}.
Hence, (A B)′ = A′ B′. [Each = {1, 6}]
Question 214:
If X and Y are two sets such that X Y has 50 students, X has 28 elements and Y has 32 elements, how many elements does X Y have ?
Answer:
We know that
n(X Y) = n(X) + n(Y) – n(X Y).
50 = 28 + 32 – n(X Y).
Hence, n(X Y) = 60 – 50 = 10.
Question 215:
In a school there are 20 teachers who teach Mathematics or Physics. Of these, 12 teach Mathematics and 4 teach both Physics and Mathematics. How many teach Physics ?
Answer:
Let
M = Set of teachers who teach Mathematics
and P = Set of teachers who teach Physics.
By the question, n(M P) = 20, n(M) = 12 and
n(M P) = 4.
Now n(M P) = n(M) + n(P) – n(M P)
20 = 12 + n(P) – 4
n(P) = 24 – 12 = 12.
Hence, 12 teachers teach Physics.
Question 216:
In a class of 35 students, 24 like to play cricket and 16 like to play football. Also, each student likes to play atleast one of the two games. How many students like to play both cricket and football ?
Answer:
Let C = Set of students who like cricket
and F = Set of students who like football.
We know that n(C F) = n(C) + n(F) – n(C F)
35 = 24 + 16 – n(C F)
n(C F) = 40 – 35 = 5.
Hence, 5 students like to paly both cricket and football.
Question 217:
In a survey of 400 students in a school, 110 were listed as taking Apple Juice, 140 as taking Orange Juice and 85 were listed as taking both Apple as well as orange Juice. Find how many students were taking neither Apple juice nor Orange Juice.
Answer:
Let A = Set of students who take Apple Juice.
and O = Set of students who take Orange juice.
By the question,
n(A) = 110, n(O) = 140, n(A O) = 85.
Now n(A O) = n(A) + n(O) – n(A O)
= 110 + 140 –85 = 165.
Total no. of students = 400.
No. of students who take neither Apply Juice nor Orange
Juice
= 400 – 165 = 235.
Question 218:
There are 200 individuals with a skin disorder. 120 had been exposed to the chemical C1, 50 to chemical C2 and 30 to both the chemicals C1 and C2. Find the number of individuals exposed to : Chemical C1 but not Chemical C2
Answer:
Let U = Set of individuals, suffering from
skin disorder,
A = Set of individuals exposed to
Chemical C1
and B = Set of individuals exposed to
Chemical C2.
By the question, n (U) = 200, n (A) = 120, n (B) = 50
and n (A B) = 30.
From Venn Diagram
A = (A – B) (A B)
n (A) = n (A – B) + n (A B)
[ (A – B) and (A B) are disjoint]
n (A – B) = n (A) – n (A B)
= 120 – 30 = 90.
Hence, the number of individuals exposed to Chemical
C1 but not to Chemical C2 = 90.
Question 219:
There are 200 individuals with a skin disorder. 120 had been exposed to the chemical C1, 50 to chemical C2 and 30 to both the chemicals C1 and C2. Find the number of individuals exposed to : Chemical C2 but not Chemical C1
Answer:
Let U = Set of individuals, suffering from
skin disorder,
A = Set of individuals exposed to
Chemical C1
and B = Set of individuals exposed to
Chemical C2.
By the question, n (U) = 200, n (A) = 120, n (B) = 50
and n (A B) = 30.
From Venn Diagram,
B = (B – A) (A B)
n (B) = n (B – A) + n (A B)
[ (B – A ) and (A B) are disjoint]
n (B – A) = n (B) – n (A B)
= 50 – 30 = 20.
Hence, the number of individuals exposed to Chemical
C2 but not to Chemical C1 = 20.
Question 220:
There are 200 individuals with a skin disorder. 120 had been exposed to the chemical C1, 50 to chemical C2 and 30 to both the chemicals C1 and C2. Find the number of individuals exposed to : Chemical C1 or Chemical C2.
Answer:
Let U = Set of individuals, suffering from
skin disorder,
A = Set of individuals exposed to
Chemical C1
and B = Set of individuals exposed to
Chemical C2.
By the question, n (U) = 200, n (A) = 120, n (B) = 50
and n (A B) = 30.
Number of individuals exposed to either Chemical
C1 or to Chemical C2
= n (A B)
= n (A) + n (B) – n (A B)
= 120 + 50 – 30 = 170 – 30 = 140.
Question 221:
Show that the set of letters needed to spell “CATARACT” and the set of letters needed to spell “TRACT” are equal.
Answer:
For “CATARACT”, the set is A = {C, A, T, R}. For “TRACT”, the set is B = {T, R, A, C}. Hence, A = B. [ A and B have same elements]
Question 222:
List all the subsets of the set {–1, 0, 1}.
Answer:
To subsets are :
, {–1}, {0}, {1}, {–1, 0}, {–1, 1}, {0, 1}, {–1, 0, 1}.
Question 223:
Show that A B = A B implies A = B.
Answer:
In order to prove that A = B, we have to prove
that :
A B and B A.
Let a A. Then a A B
a A B [ A B = A B]
a B.
A B ...(1)
Similarly if b B, then b A B
b A B [ A B = A B]
b A.
B A ...(2)
From (1) and (2),A = B.
Question 224:
For any sets A and B, show that :
P(A B) = P(A) P(B).
Answer:
In order to prove that
P(A B) = P(A) P(B), we have to prove that :
P(A B) P(A) P(B) and P(A) P(B) P(A B).
Firstly, Let X P(A B).
Now X P(A B) X A B
X A and X B
X P(A) and X P(B)
X P(A) P(B).
P(A B) P(A) P(B) ...(1)
Now Y P(A) P(B)
Y P(A) and Y P(B)
Y A and Y B Y A B
Y P(A B) ...(2)
P(A) P(B) P(A B)
From (1) and (2), P(A B) = P(A) P(B).
Question 225:
A market research group conducted a survey of 1000 consumers and reported that 720 consumers liked product A and 450 liked product B. What is the least number that must have liked both products ?
Answer:
Let U = Set of consumers surveyed
A = Set of consumers who liked
product (A)
and B = Set of consumers who liked
product (B).
By the question, n (U) = 1000, n (A) = 720
and n (B) = 450.
Now n (A B) = n (A) + n (B) – n (A B)
= 720 + 450 – n (A B)
= 1170 – n (A B)
n (A B) = 1170 – n (A B) ...(1)
Thus n (A B) is least when n (A B) is maximum.
But A B U n (A B) ≤ n (U) = 1000
Max. n (A B) = 1000.
From (1), least n (A B) = 1170 – 1000 = 170.
Hence, the least number of consumers who liked both
products = 170.
Question 226:
A market research group conducted a survey of 1000 consumers and reported that 720 consumers liked product A and 450 liked product B. What is the least number that must have liked both products ?
Answer:
Let U = Set of consumers surveyed
A = Set of consumers who liked
product (A)
and B = Set of consumers who liked
product (B).
By the question, n (U) = 1000, n (A) = 720
and n (B) = 450.
Now n (A B) = n (A) + n (B) – n (A B)
= 720 + 450 – n (A B)
= 1170 – n (A B)
n (A B) = 1170 – n (A B) ...(1)
Thus n (A B) is least when n (A B) is maximum.
But A B U n (A B) ≤ n (U) = 1000
Max. n (A B) = 1000.
From (1), least n (A B) = 1170 – 1000 = 170.
Hence, the least number of consumers who liked both
products = 170.
Question 227:
Out of 500 car owners investigated, 400 owned car A and 200 owned car B, 50 owned both A and B cars. Is this data correct ?
Answer:
Let U = Set of car owners investigated
A = Set of persons who owned car A
and B = Set of persons who owned car B.
By the question, n (U) = 500, n (A) = 400,
n (B) = 200 and n (A B) = 50.
Now n (A B) = n (A) + n (B) – n (A B)
= 400 + 200 – 50 = 550.
But A B U n (A B) ≤ n (U) = 500.
This is a contradiction.
Hence, the given data is incorrect.
Question 228:
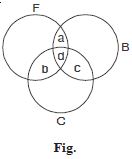
A college awarded 38 medals in football, 15 in basketball and 20 in cricket. If these medals went to a total of 58 men and only three men got medals in all the three sports, how many received medals in exactly two of the three sports ?
Answer:
Let F, B and C denote the set of men who
received medals in Football, Basketball and Cricket
respectively.
By the question,
n(F) = 38, n(B) = 15,
n(C) = 20, n(F B C) = 58
and n (F B C) = 3.
Now n(F B C) = n(F) + n(B)
+ n(C) – n(F B) – n(F C) – n(B C) + n(F B C)
58 = 38 + 15 + 20 – n(F B)
– n(F C) – n(B C) + 3
n(F B) + n(F C) + n(B C) = 18.
Let a denote the number of men who got medals in
Football and basketball ; etc.
Now d = n(F B C) = 3
and a + d + b + d + c + d = 18
a + b + c = 18 – 3d = 18 –3(3) = 9.
Hence, 9 men got medals in exactly two of the three
sports.