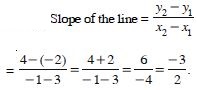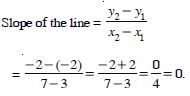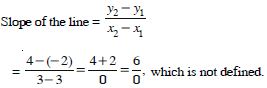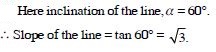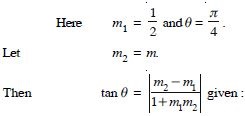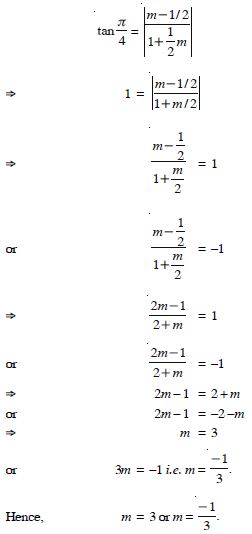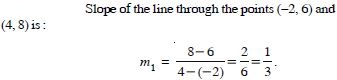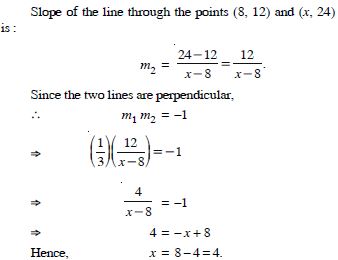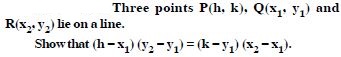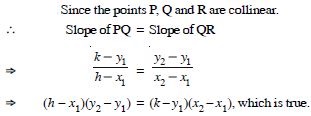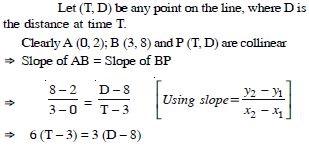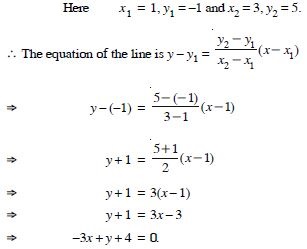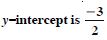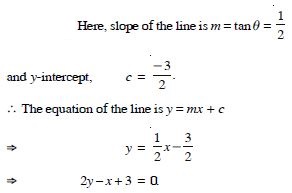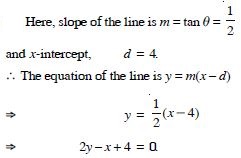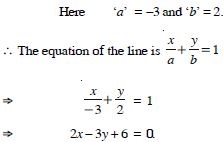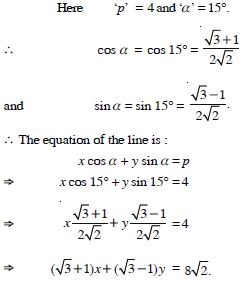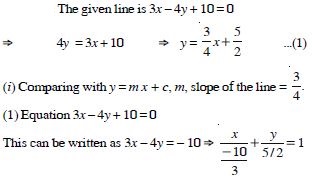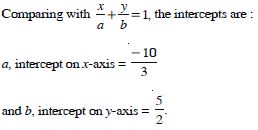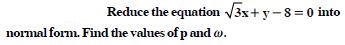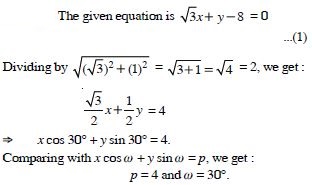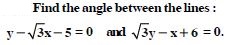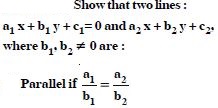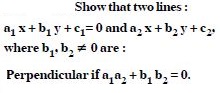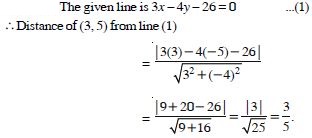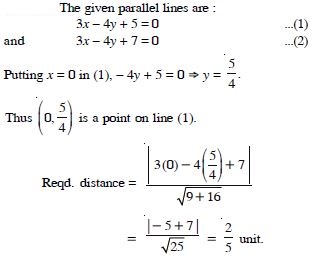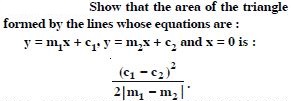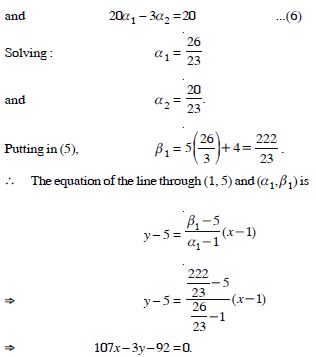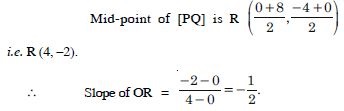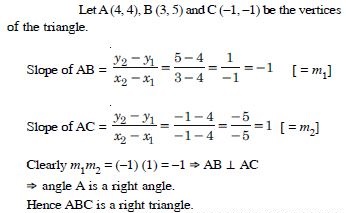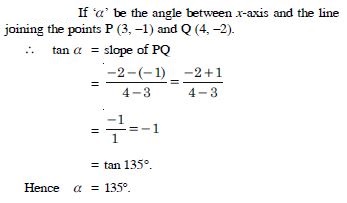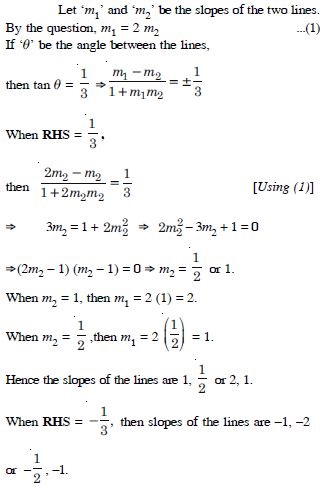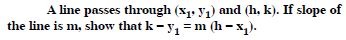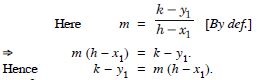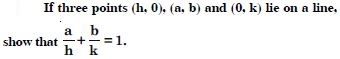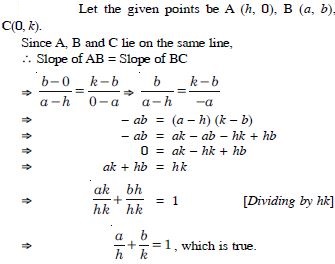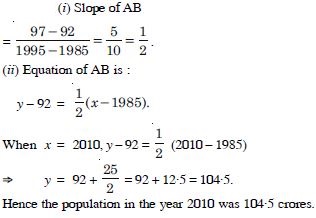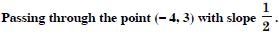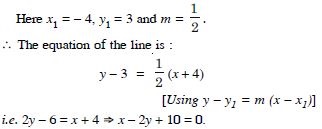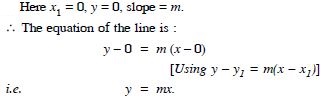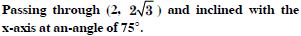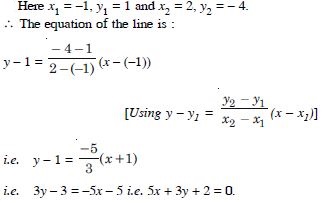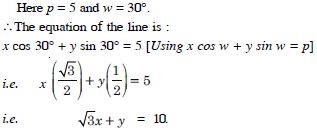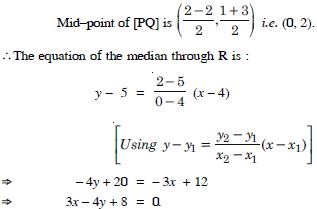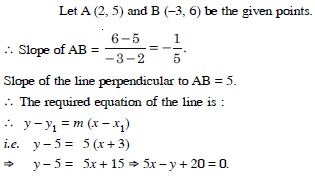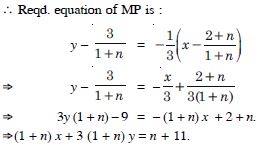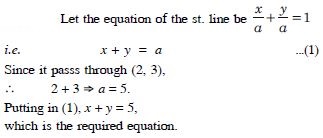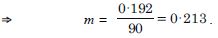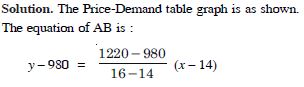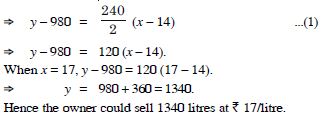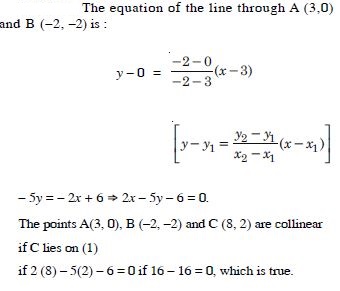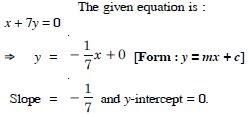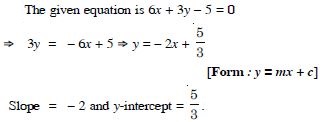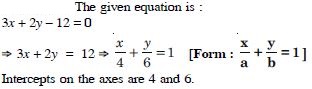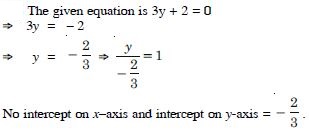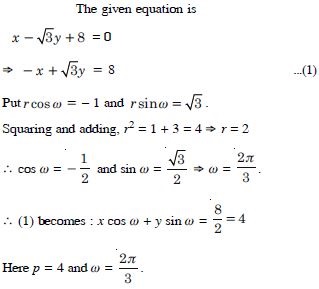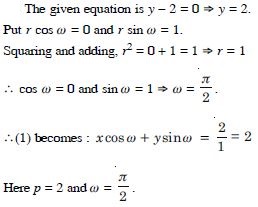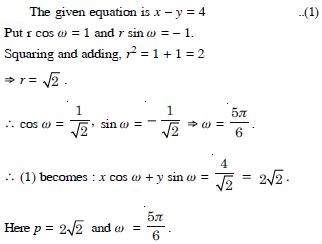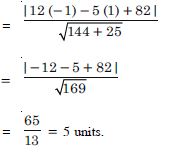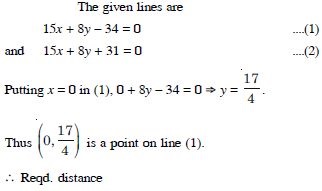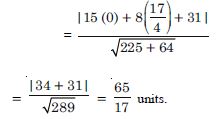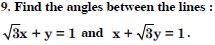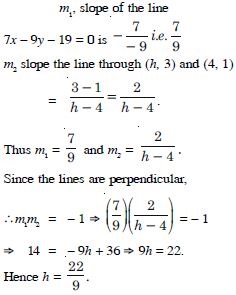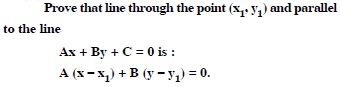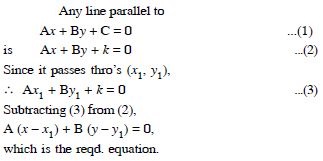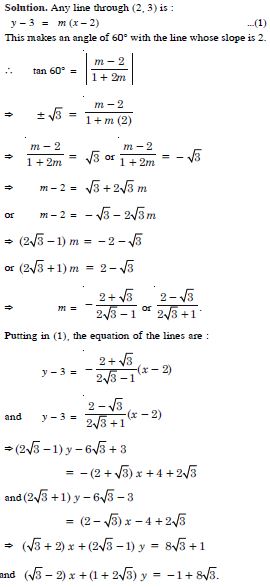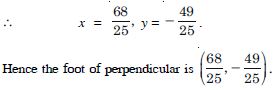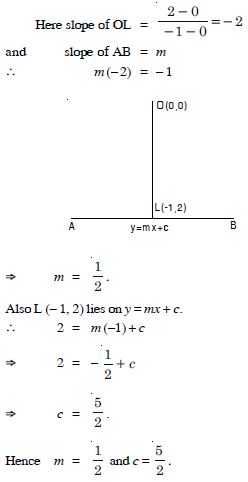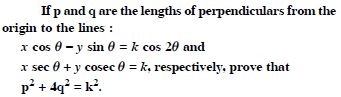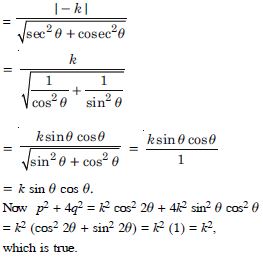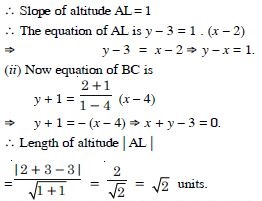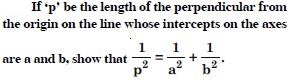NCERT Solutions for Class 11 Math Chapter 10 - Straight Lines

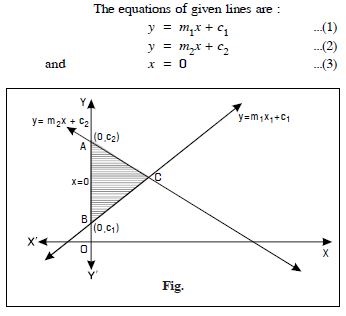
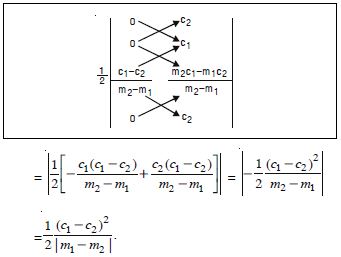
Question 1:

Find the slope of the line :
Passing through the points (3, –2) and (–1

Question 2:

Find the slope of the line :
Passing through the points (3, –2) and (7, –2)

Question 3:

Find the slope of the line :
Passing through the points (3, –2) and (3, 4)

Question 4:

Find the slope of the line :
Making inclination of 60$°$ with the positive direction of x-axis.

Question 5:

Question 6:

Line through the points (–2, 6) and (4, 8) is perpendicular to the line through the points (8, 12) and (x, 24). Find the value of ‘x’.

Question 7:

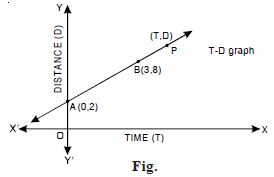
Question 8:

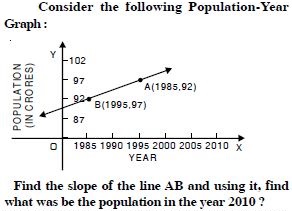
In the figure, time-distance graph of a linear relation is given :
Two positions of time and distance recorded as :
When T = 0, D = 2 and when T = 3, D = 8.
Using the concept of slope, find the law of motion i.e. how distance depends upon time.

Question 9:

Find the equations of the lines parallel to axes and passing through (–2, 3).

Question 10:

Find the equation of line through (–2, 3) with slope – 4.

Question 11:

Write the equation of the line through the points (1, –1) and (3, 5).

Question 12:

Question 13:

x-intercept is 4

Question 14:

Find the equation of the line, which makes intercepts –3 and 2 on the x- and y-axes respectively.

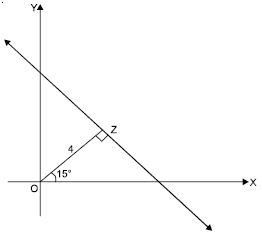
Question 15:

Find the equation of the line whose perpendicular distance from the origin is 4 units and the angle which the normal makes with positive direction of x-axis is 15$°$.

Question 16:

The Fahrenheit temperature F and absolute temperature K satisfy a linear equation. Given K = 273 when F = 32 and that K = 373 when F = 212. Express K in terms of F and the value of F when K = 0.

Question 17:

Equation of a line is 3x – 4y + 10 = 0. Find its :
(i) slope (ii) x- and y-intercepts

Question 18:

Question 19:

Question 20:

Question 21:

Question 22:

Find the equation of a line perpendicular to the line x – 2y + 3 = 0 and passing through the point (1, –2).

Question 23:

Find the distance of the point (3, –5) from the line 3x – 4y – 26 = 0.

Question 24:

Find the distance between the parallel lines :
3x – 4y + 5 = 0 and 3x – 4y + 7 = 0.

Question 25:

If the lines :
2x + y – 3 = 0, 5x + ky – 3 = 0 and 3x – y – 2 = 0 are concurrent, find the value of ‘k’.

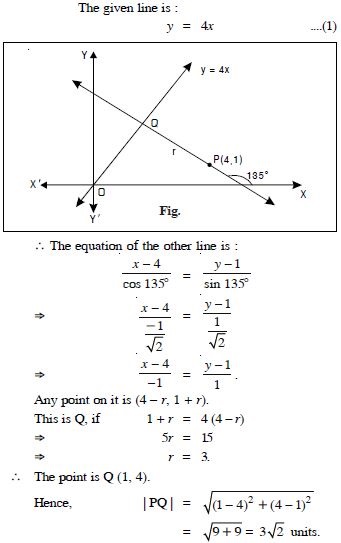
Question 26:

Find the distance of the line 4x – y = 0 from the point P(4, 1) measured along the line making an angle of 135$°$ with the positive x-axis.

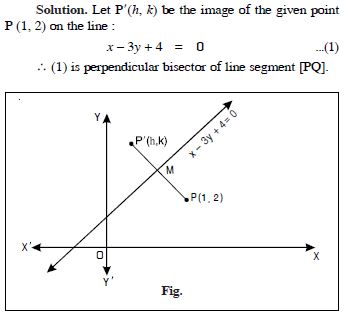
Question 27:

Assuming that straight line works as the plane mirror for a point, find the image of the point (1, 2) in the line x – 3y + 4 = 0.

Question 28:

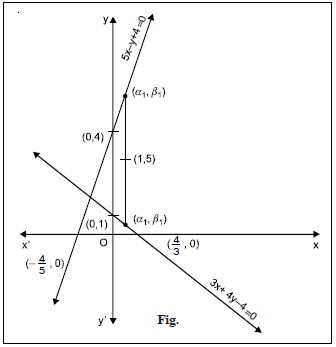
Question 29:

A line is such that its segment between the lines :
5x – y + 4 = 0 and 3x + 4y – 4 = 0 is bisected at the point (1, 5). Obtain its equation.

Question 30:

Show that the path of a moving point such that its distance from the lines :
3x – 2y = 5 and 3x + 2y = 5 are equal, is a straight line.

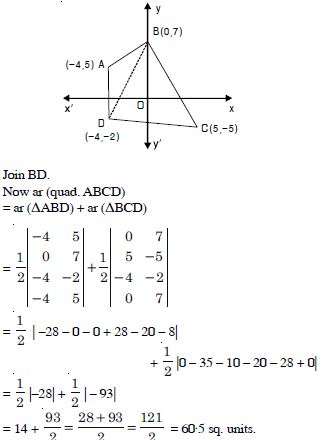
Question 31:

Draw a quadrilateral in the cartesian plane whose vertices are (– 4, 5), (0, 7), (5, –5) and (– 4, –2). Also find its area.

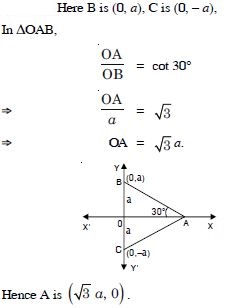
Question 32:

The base of an equilateral triangle with side 2a lies along the y-axis such that the mid–point of the base is the origin. Find the vertices of the triangle.

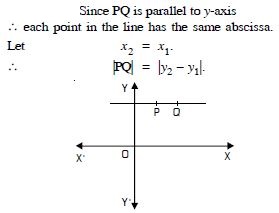
Question 33:

PQ is parallel to y-axis

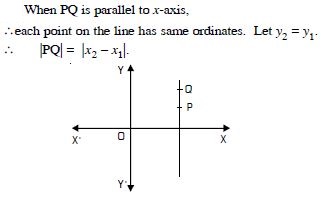
Question 34:

PQ is parallel to x-axis

Question 35:

Find a point on the x-axis, which is equidistant from (7, 6) and (3, 4).

Question 36:

Find the slope of the line, which passes through the origin and the mid-point of the line segment joining the points P (0, –4) and Q (8, 0).

Question 37:

Without using Pythagorean Theorem, show that (4, 4), (3, 5) and (–1, –1) are vertices of a right triangle.

Question 38:

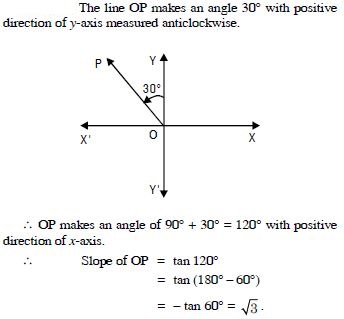
Find the slope of the line which makes an angle of 30$°$ with the positive direction of y-axis, measured anticlockwise.

Question 39:

Find the value of x for which the points (x, –1), (2, 1) and (4, 5) are collinear.

Question 40:

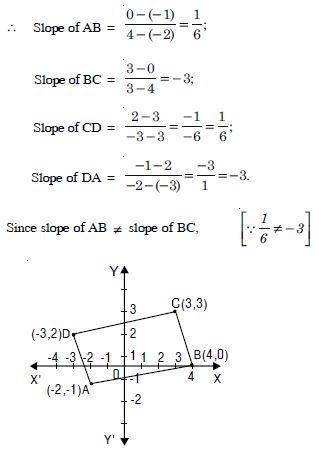
Without using the distance formula, show that (–2, –1), (4, 0), (3, 3) and (–3, 2) are the vertices of a parallelogram.

Question 41:

Find the angle between the x-axis and the line joining the points (3, –1) and (4, –2).

Question 42:

Question 43:

Question 44:

Question 45:

Question 46:

find the equation of the line, which satisfy the given conditions :

Question 47:

find the equation of the line, which satisfy the given conditions :

Question 48:

find the equation of the line, which satisfy the given conditions :

Question 49:

find the equation of the line, which satisfy the given conditions :

Question 50:

find the equation of the line, which satisfy the given conditions :

Question 51:

find the equation of the line, which satisfy the given conditions :
Intersecting the y-axis at a distance of 2 units above the origin and making an angle of 30$°$ with positive direction of the x-axis.

Question 52:

find the equation of the line, which satisfy the given conditions :
Passing through the points (–1, 1) and (2, –4).

Question 53:

find the equation of the line, which satisfy the given conditions :
Perpendicular distance from the origin is 5 units and the angle made by the perpendicular with the positive x-axis is 30$°$.

Question 54:

The vertices of a triangle PQR are P (2, 1), Q (–2, 3) and R (4, 5). Find the equation of the median through the vertex R.

Question 55:

Find the equation of the line through (–3, 5) and perpendicular to the line through the points (2, 5) and (–3, 6).

Question 56:

A line perpendicular to the line segment joining the points (1, 0) and (2, 3) divides it in the ratio 1 : n. Find the equation of the line.

Question 57:

Find the equation of a line that cuts off equal intercepts on the co-ordinate axes and passes through the point (2, 3).

Question 58:

Find the equation of a straight line passing through the point (2, 2) such that the sum of its intercepts on the axes is 9.

Question 59:

Question 60:

The perpendicular from the origin to a line meets it at the point (–2, 9), find the equation of the line.

Question 61:

The length L (in centimetres) of a copper rod is a linear function of its Celsius temperature C. In an experiment, if L = 124·942 when C = 20 and L = 125·134 when C = 110, express L in terms of C.

Question 62:

Question 63:

Question 64:

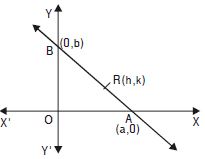
Point R (h, k) divides a line segment between the axes in the ratio 1 : 2. Find the equation of the line.

Question 65:

By using the concept of the equation of a line, prove that three points (3, 0), (–2, –2) and (8, 2) are collinear.

Question 66:

Reduce the following equations into slope-intercept form and find their slopes and the y-intercepts :
x + 7y = 0

Question 67:

Reduce the following equations into slope-intercept form and find their slopes and the y-intercepts :
6x + 3y – 5 = 0

Question 68:

Reduce the following equations into slope-intercept form and find their slopes and the y-intercepts :
y = 0

Question 69:

Reduce the following equations into intercept form and find their intercepts on the axes :
3x + 2y – 12 = 0

Question 70:

Reduce the following equations into intercept form and find their intercepts on the axes :
4x – 3y = 6

Question 71:

Reduce the following equations into intercept form and find their intercepts on the axes :
3y + 2 = 0

Question 72:

Reduce the following equations into normal form. Find their perpendicular distance from the origin and angle between perpendicular and the positive x-axis.

Question 73:

Reduce the following equations into normal form. Find their perpendicular distance from the origin and angle between perpendicular and the positive x-axis.
y – 2 = 0

Question 74:

Reduce the following equations into normal form. Find their perpendicular distance from the origin and angle between perpendicular and the positive x-axis.
x – y = 4

Question 75:

Find the distance of the point (– 1, 1) from the line :
12 (x + 6) = 5 (y – 2).

Question 76:

Question 77:

Find the distance between the parallel lines :
15x + 8y – 34 = 0 and 15x + 8y + 31 = 0

Question 78:

Find the distance between the parallel lines :
l (x + y) + p = 0 and l (x + y) – r = 0

Question 79:

Find the equation of the line parallel to the line 3x – 4y + 2 = 0 and passing through the point (– 2, 3).

Question 80:

Find equation of the line perpendicular to the line x – 7y + 5 = 0 and having x-intercept 3.

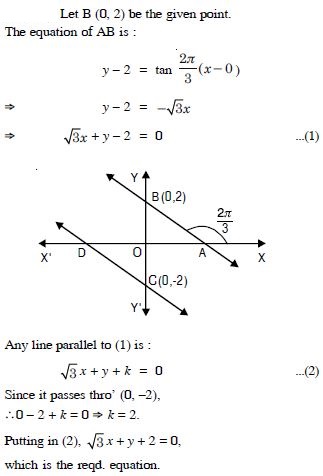
Question 81:

Question 82:

The line through the points (h, 3) and (4, 1) intersects the line 7x – 9y – 19 = 0 at right angle. Find the value of h.

Question 83:

Question 84:

Two lines passing through the point (2, 3) intersect each other at an angle of 60°. If the slope of one line is 2, find the equation of the other line

Question 85:

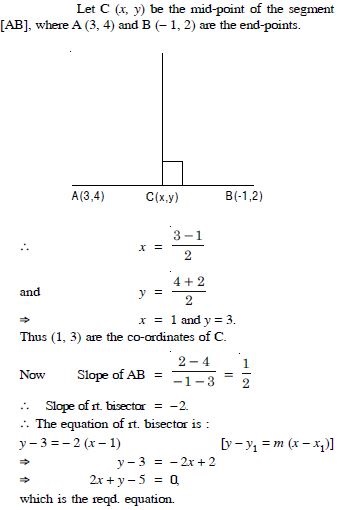
Find the equation of right-bisector of segment joining (3, 4) and (– 1, 2).

Question 86:

Find the co-ordinates of the foot of perpendicular from a point (– 1, 3) to the line 3x – 4y – 16 = 0.

Question 87:

The perpendicular from the origin to the line y = mx + c meets it at the point (– 1, 2). Find the values of m and c.

Question 88:

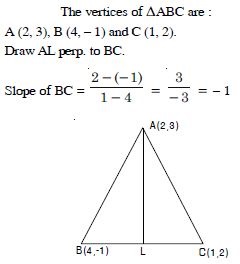
Question 89:

In the triangle ABC with vertices A (2, 3), B (4, – 1) and C (1, 2), find the equation and length of altitude from the vertex A.

Question 90: