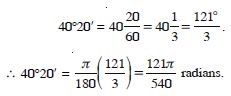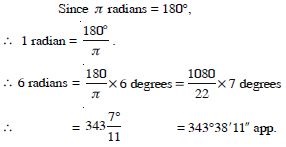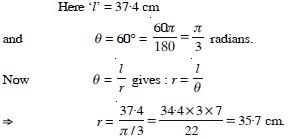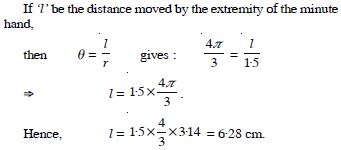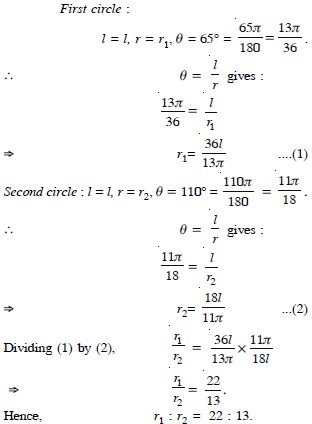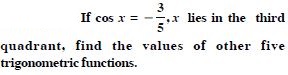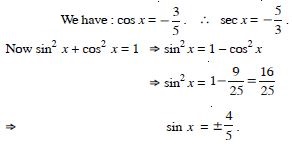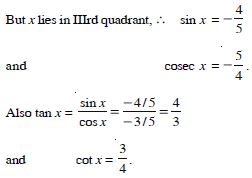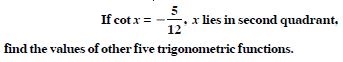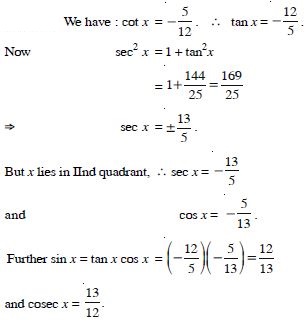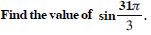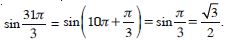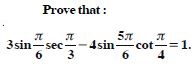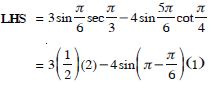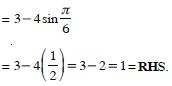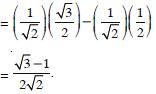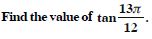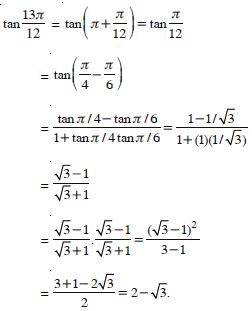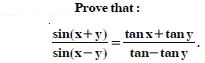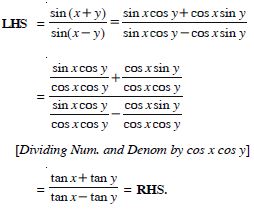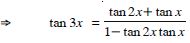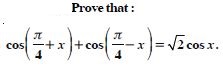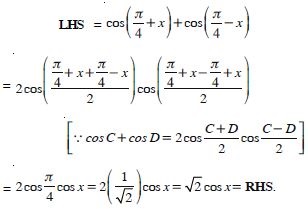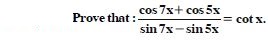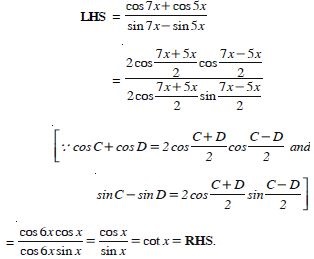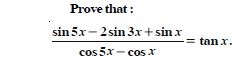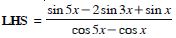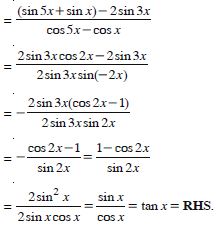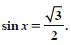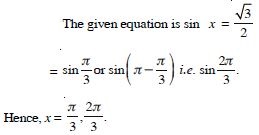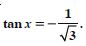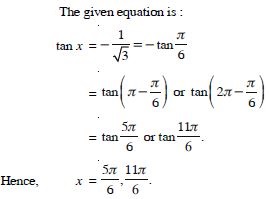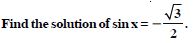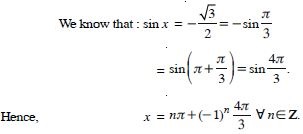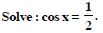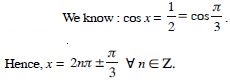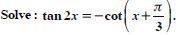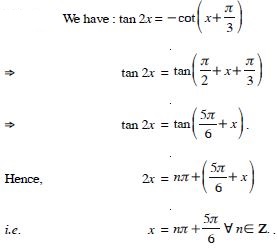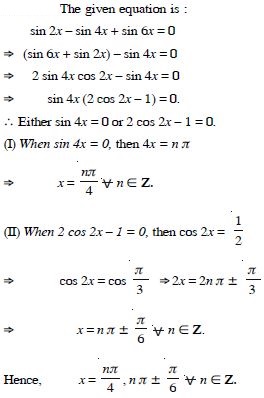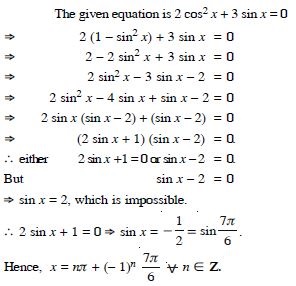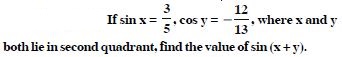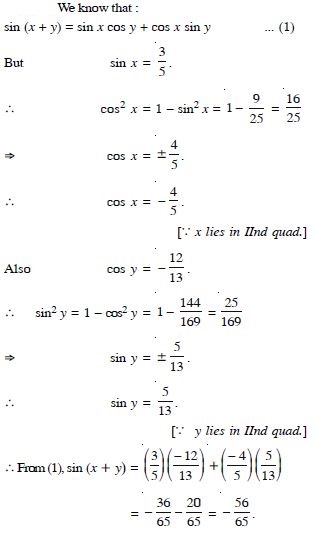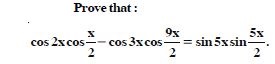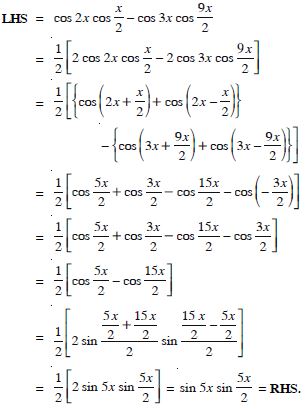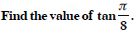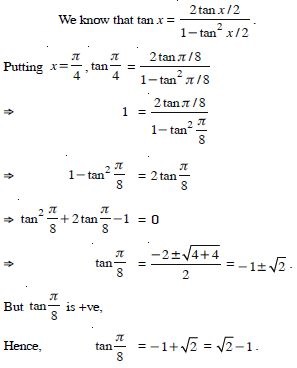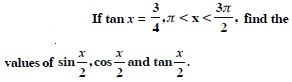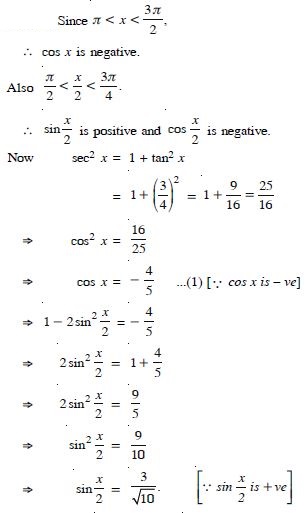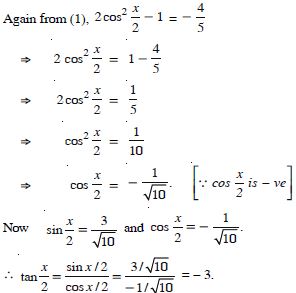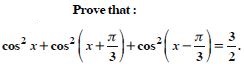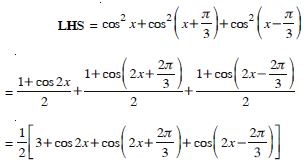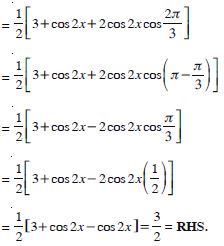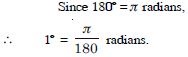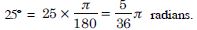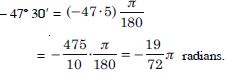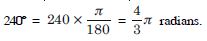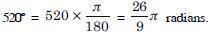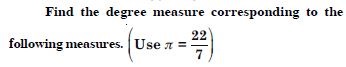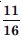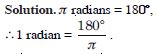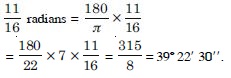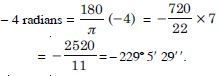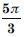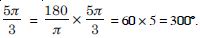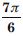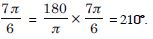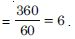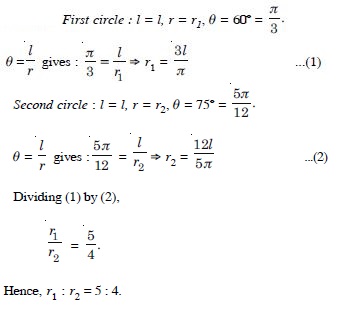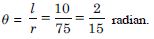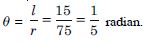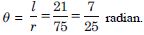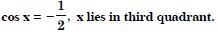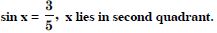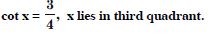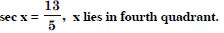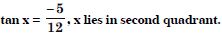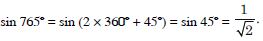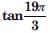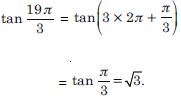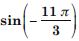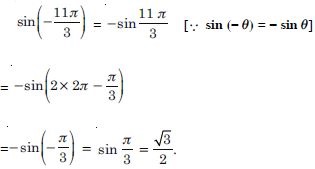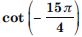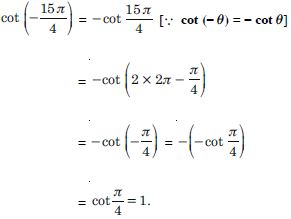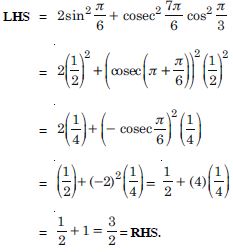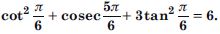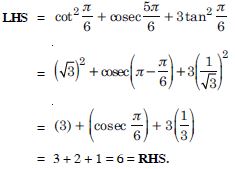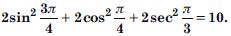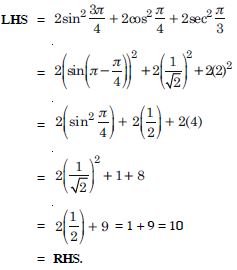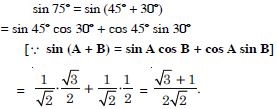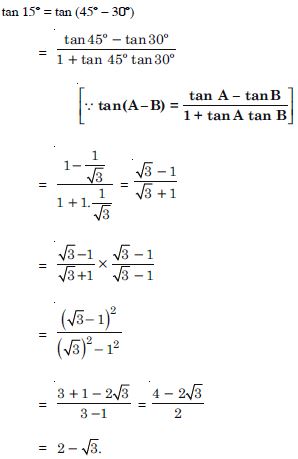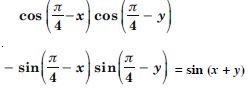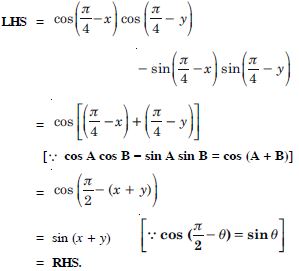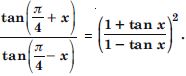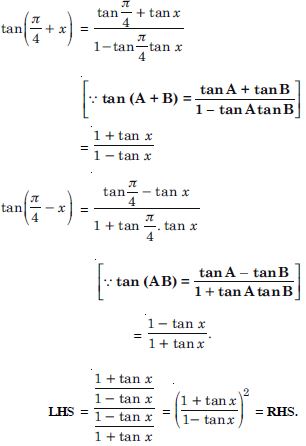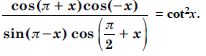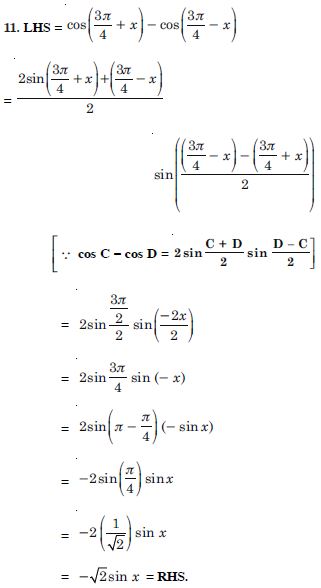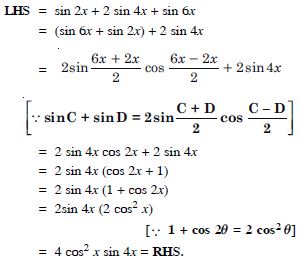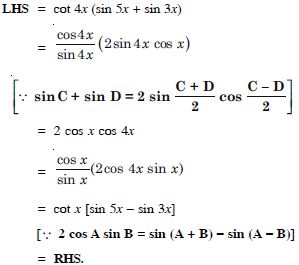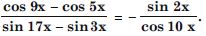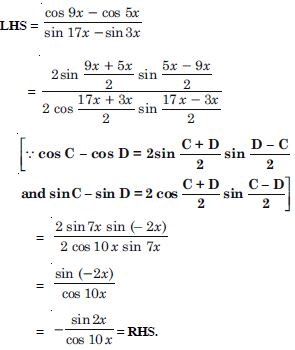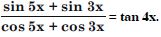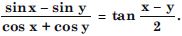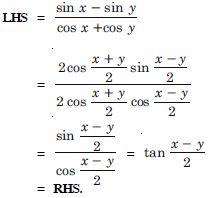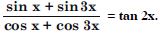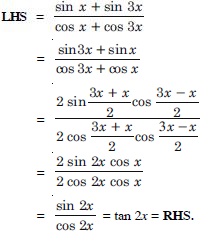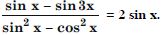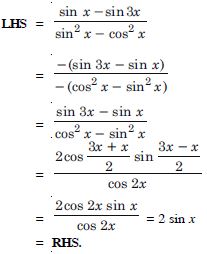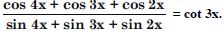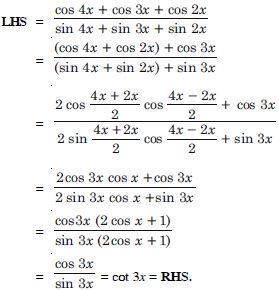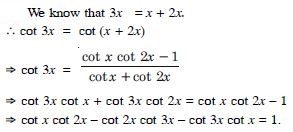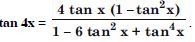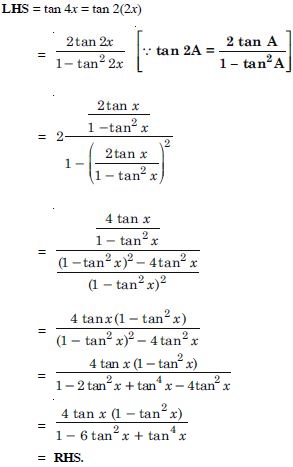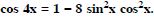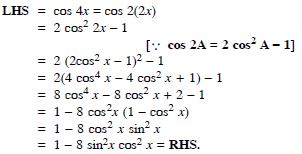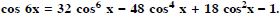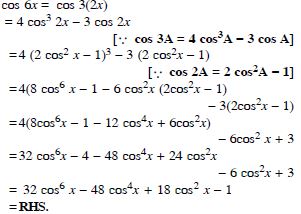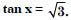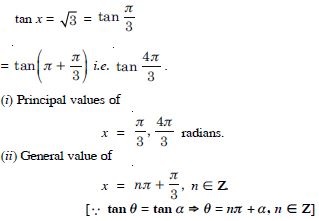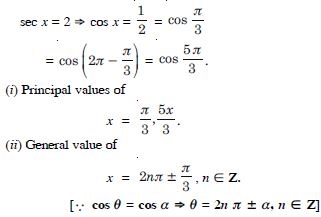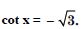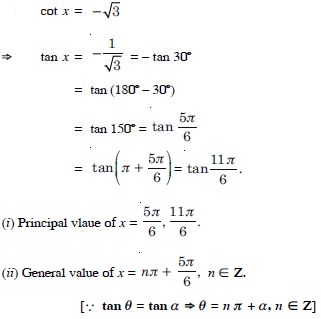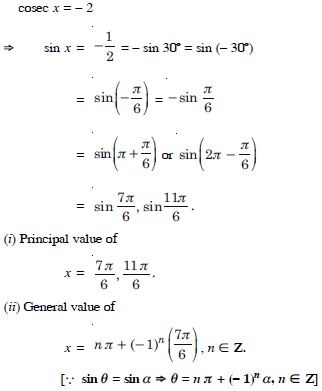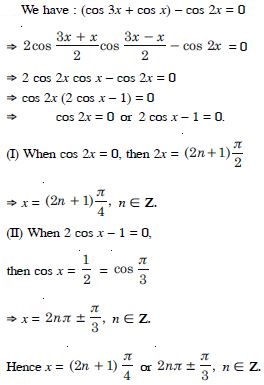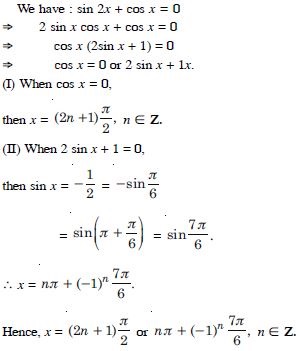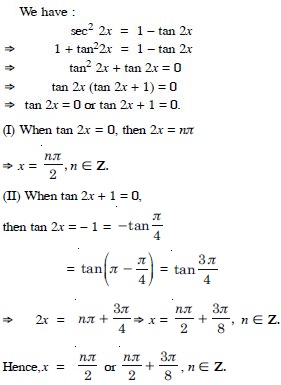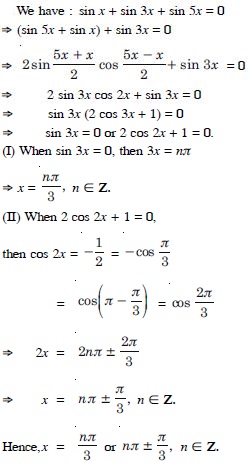NCERT Solutions for Class 11 Math Chapter 3 - Trigonometric

Question 1:

Convert 40$°$20′ into radian measure.

Question 2:

Convert 6 radians into degree measure.

Question 3:

Find the radius of the circle in which a
central angle of 60$°$ intercepts an arc of length 37·4 cm. (Use $\mathrm{\pi }$= 22/7)

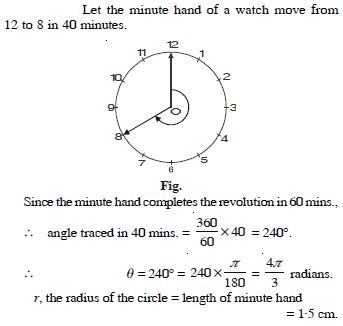
Question 4:

The minute hand of a watch is 1·5 cm long. How far does its tip move in 40 minutes ?
(Use $\mathrm{\pi }$ = 3.14)

Question 5:

If the arcs of the same length in two circles subtend angles 65$°$ and 110$°$ at the centre, find the ratio of their radii.

Question 6:

Question 7:

Question 8:

Question 9:

Find the value of cos (– 1710$°$).

Question 10:

Question 11:

Find the value of sin 15$°$.

Question 12:

Question 13:

Question 14:

Show that :
tan 3x tan 2x tan x = tan 3x – tan 2x – tan x.

Question 15:

Question 16:

Question 17:

Question 18:

Find the principal solution of the equation :

Question 19:

Find the principal solution of the equation :

Question 20:

Question 21:

Question 22:

Question 23:

Solve : sin 2x – sin 4x + sin 6x = 0.

Question 24:

Solve : 2 cos² x + 3 sin x = 0.

Question 25:

Question 26:

Question 27:

Question 28:

Question 29:

Question 30:

Find the radian measures corresponding to the following degree measures :
25$°$

Question 31:

Find the radian measures corresponding to the following degree measures :
– 47$°$ 30′

Question 32:

Find the radian measures corresponding to the following degree measures :
240$°$

Question 33:

Find the radian measures corresponding to the following degree measures :
520$°$

Question 34:

Question 35:

– 4

Question 36:

Question 37:

Question 38:

wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second ?

Question 39:

Find in degree measure of the angle subtended at the centre of a circle of radius 100 cm. by an arc of 22 cm.
(Use $\mathrm{\pi }$ = 22/7)

Question 40:

In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of the minor arc of the circle.

Question 41:

If in two circles, arcs of the same length subtend angles of 60$°$ and 75$°$ at the centre, find the ratio of their radii.

Question 42:

Find the angle through which a pendulum swings if its length is 75 cm and the tip-describes an arc of length :
10 cm

Question 43:

Find the angle through which a pendulum swings if its length is 75 cm and the tip-describes an arc of length :
15 cm

Question 44:

Find the angle through which a pendulum swings if its length is 75 cm and the tip-describes an arc of length :
21 cm

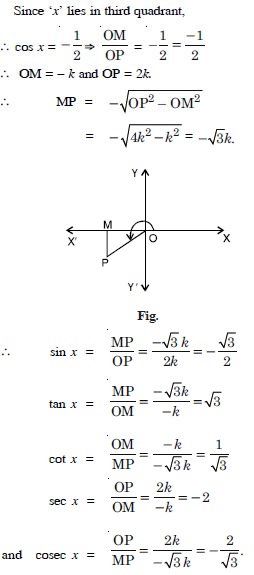
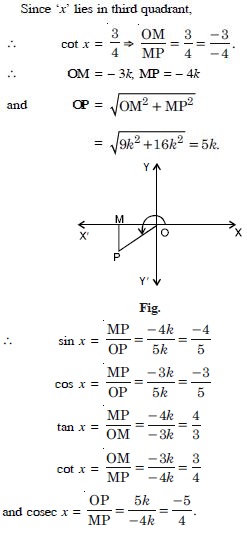
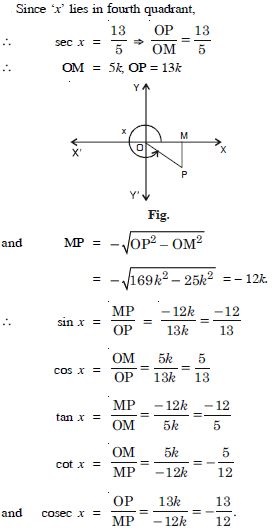
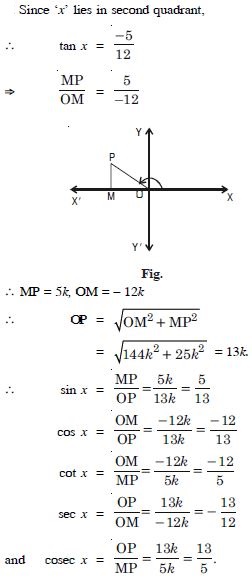
Question 45:

Find the values of other five trigonometric
functions:

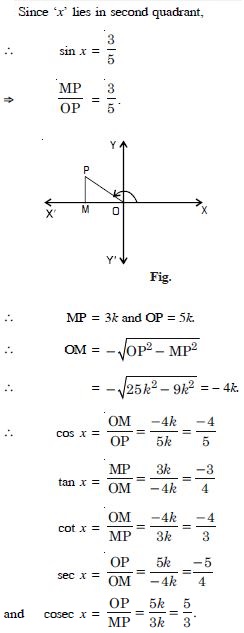
Question 46:

Find the values of other five trigonometric
functions:

Question 47:

Find the values of other five trigonometric
functions:

Question 48:

Find the values of other five trigonometric
functions:

Question 49:

Find the values of other five trigonometric
functions:

Question 50:

Find the values of the trigonometric function:
sin 765$°$

Question 51:

Find the values of the trigonometric function:
cosec (– 1410$°$)

Question 52:

Find the values of the trigonometric function:

Question 53:

Find the values of the trigonometric function:

Question 54:

Find the values of the trigonometric function:

Question 55:

Prove that:

Question 56:

Prove that:

Question 57:

Prove that:

Question 58:

Prove that:

Question 59:

Find the value of :
sin 75$°$

Question 60:

Find the value of :
tan 15$°$

Question 61:

Prove the following:

Question 62:

Prove the following:

Question 63:

Prove the following:

Question 64:

Prove the following:

Question 65:

Prove the following:
sin (x + 1)x sin (x + 2) x + cos (x + 1)x cos (x + 2)x = cos x.

Question 66:

Prove the following:

Question 67:

Prove the following:
sin² 6x – sin² 4x = sin 2x sin 10x.

Question 68:

Prove the following:
cos² 2x – cos² 6x = sin 4x sin 8x

Question 69:

Prove the following:
sin 2x + 2 sin 4x + sin 6x = 4 cos²x sin 4x.

Question 70:

Prove the following:
cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x).

Question 71:

Prove the following:

Question 72:

Prove the following:

Question 73:

Prove the following:

Question 74:

Prove the following:

Question 75:

Prove the following:

Question 76:

Prove the following:

Question 77:

Prove the following:
cot x cot 2x – cot 2x cot 3x – cot 3x cot x = 1.

Question 78:

Prove the following:

Question 79:

Prove the following:

Question 80:

Prove the following:

Question 81:

Find the principal and general solutions of the following equations :

Question 82:

Find the principal and general solutions of the following equations :
sec x = 2.

Question 83:

Find the principal and general solutions of the following equations :

Question 84:

Find the principal and general solutions of the following equations :
cosec x = – 2.

Question 85:

Find the general solution for each of the following
equations :
cos 4x = cos 2x.

Question 86:

Find the general solution for each of the following
equations :
cos 3x + cos x – cos 2x = 0

Question 87:

Find the general solution for each of the following
equations :
sin 2x + cos x = 0.

Question 88:

Find the general solution for each of the following
equations :
sec² 2x = 1 – tan 2x.

Question 89:

Find the general solution for each of the following
equations :
sin x + sin 3x + sin 5x = 0.