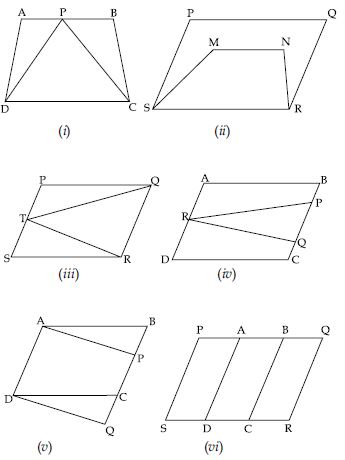
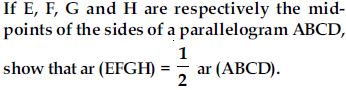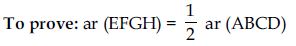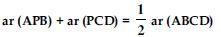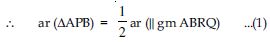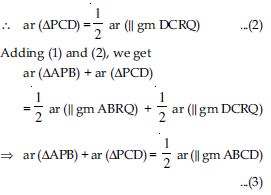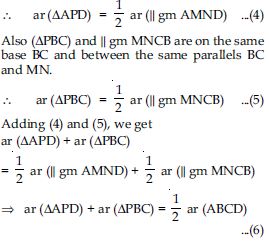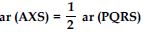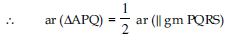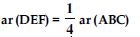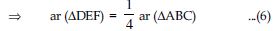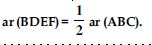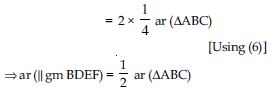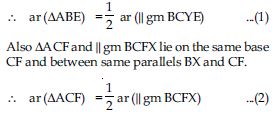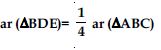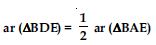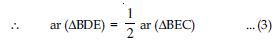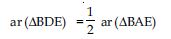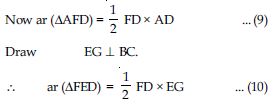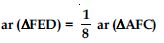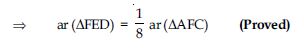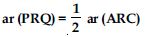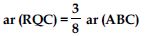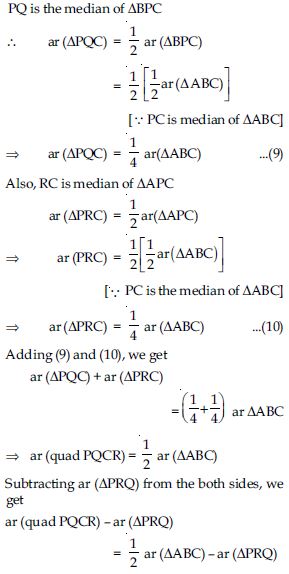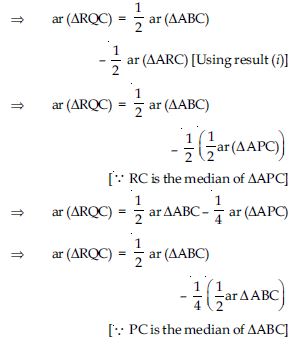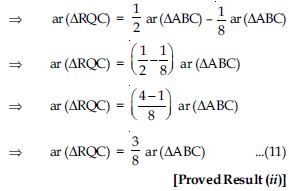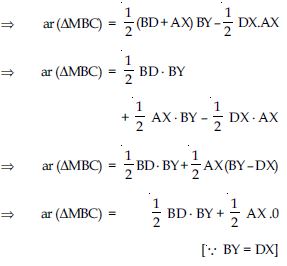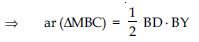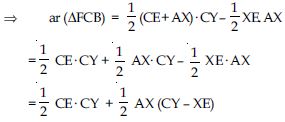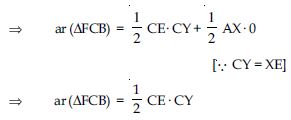Question 1:
Which of the following figures lies on the same base and between the same parallels. In such a case, write the common base and the two parallels.
Answer:
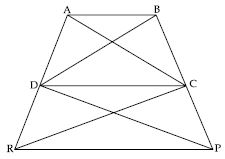
In Fig. (i); DPC and trap. ABCD are on the same base DC and between same parallels DC and AB.
In Fig. (iii); RTQ and parallelogram PQRS are on the same base QR and between same parallels QR and
PS.
In Fig. (v); parallelogram ABCD and parallelogram APQD are on the same base AD and between
the same parallels AD and BQ.
Question 2:
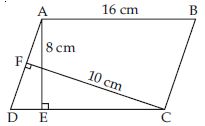
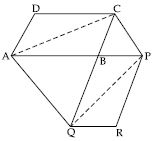
In fig. ABCD is a parallelogram; AE DC and CF AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
Answer:
ABCD is a parallelogram.
DC = AB
DC = 16 cm
AE DC (Given)
Area of parallelogram ABCD
= DC × AE
[ar (|| gm) = Base × Corresponding
height]
= 16 cm × 8 cm
= 128 cm2
Using base AD and height CF;
Area of parallelogram = AD × CF
128 cm2 = AD × 10 cm
or AD × 10 cm = 128 cm2
AD = 12.8 cm
Question 3:
Answer:
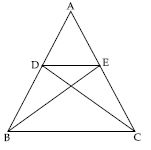
Given: ABCD is a parallelogram. Let E, F, G and H are the mid-points of sides AB, BC, CD and DA respectively.
Construction: Join AC and HF.
Proof: In ABC, E is the mid-point of side AB
and F is the mid-point of side BC.
Question 4:
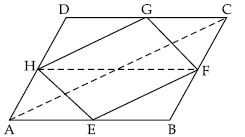
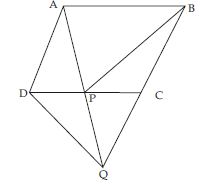
P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
Answer:
Given: ABCD is a parallelogram. P is a point on DC and Q is a point on AD.
To prove: ar (APB) = ar (BQC)
Construction: Draw PM || BC and QN || DC.
Proof: Since QC is the diagonal of || gm QNCD.
From (3) and (6), we get
ar (BQC) = ar (APB)
or ar (APB) = ar (BQC) (Proved)
Question 5:
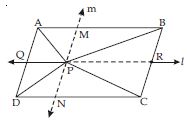
In fig., P is a point in the interior of a parallelogram ABCD. Show that
Answer:
Draw a line (say l) passing through point P and parallel to AB which intersects AD at Q and
BC at R respectively.
Now, APB and || gm ABRQ are on the same base AB and between same parallels AB and QR.
Also PCD and || gm DCRQ are on the same base DC and between same parallels DC and QR.
Question 6:
In fig., P is a point in the interior of a parallelogram ABCD. Show that
ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
Answer:
Draw a line (say m) through P and parallel to AD which intersects AB at M
and DC at N.
Now APD and ||gm AMND are on the same base AD and between same parallels AD and MN.
From (5) and (6), we get
ar (APB) + ar (PCD) = ar (APD) + ar (PBC)
or ar (APD) + ar (PBC) = ar (APB)
+ ar (PCD)
(Proved)
Question 7:
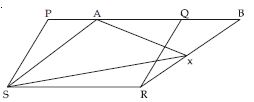
In fig., PQRS and ABRS are parallelograms and X is any point on side BR. Show that
ar (PQRS) = ar (ABRS)
Answer:
Parallelograms PQRS and ABRS are on the same base SR and between the same parallels SR and
PB.
ar (|| gm PQRS) = ar (|| gm ABRS) ...(1)
[Parallelograms on the same base and between the same parallels are equal in area.]
Question 8:
In fig., PQRS and ABRS are parallelograms and X is any point on side BR. Show that
Answer:
AXS and ||gm ABRS are on the same base AS and between the same parallels AS and BR.
Question 9:
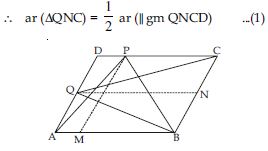
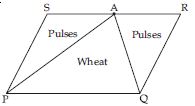
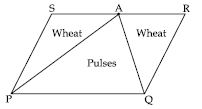
A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the field is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?
Answer:
When A is joined with P and Q; the field is divided into three parts viz. PAS, APQ and AQR.
APQ and parallelogram PQRS are on the same base PQ and between same parallels PQ and
SR.
It implies that triangular region APQ covers half portion of parallelogram shaped field
PQRS.
So, if farmer sows wheat in triangular shaped field APQ then she will definitely sow pulses
in other two triangular parts PAS and AQR.
Or
When she sows pulses in triangular shaped field APQ then she will sow wheat in other two
triangular parts PAS and AQR.
Question 10:
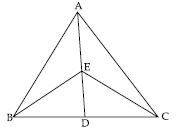
In fig. E is any point on median AD of a ABC. Show that ar (ABE) = ar (ACE).
Answer:
In ABC, AD is a median
ar (ABD) = ar (ACD) ...(1)
[ Median divides a into two s of equal area]
Again in EBC, ED is a median
ar (EBD) = ar (ECD) ...(2)
Subtracting (2) from (1), we get
ar (ABD) – ar (EBD)
= ar (ACD) – ar (ECD)
ar (ABE) = ar (ACE).
Question 11:
Answer:
Question 12:
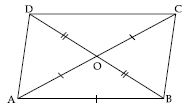
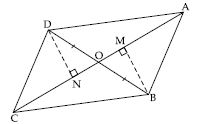
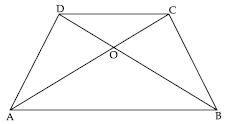
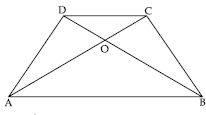
Show that the diagonals of a parallelogram divide it into four triangles of equal area.
Answer:
Let parallelogram be ABCD and its diagonals
AC and BD intersect each other at O.
In ABC and ADC,
AB = DC
(Opposite sides of parallelogram)
BC = AD
(Opposite sides of parallelogram)
AC = AC (Common)
ABC CDA
(SSS criteria of congruency)
As we know that diagonals of a parallelogram bisect each other.
In fig., O is the point of bisection.
Now in ADC; DO is the median.
ar (AOD) = ar (COD) ...(1)
( Median divides a triangle into two triangles of equal area.]
Similarly, in ABC; OB is the median.
ar (AOB) = ar (BOC) ...(2)
[Same reason as above]
In AOB and AOD; AO is the median
ar (AOB) = ar (AOD)
(Same reason as above) ...(3)
From (1), (2) and (3), we get
ar (AOB) = ar (AOD) = ar (BOC)
= ar (COD)
Thus, diagonals of a parallelogram divide it into four triangles of equal area.
Question 13:
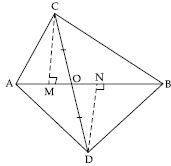
In fig. ABC and ABD are two triangles on the same base AB. If line-segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD).
Answer:
Draw CM AB and DN AB
In CMO and DNO
∠CMO = ∠DNO
[(Each = 90) construction]
∠COM = ∠DON
(Vertically opp. angles)
OC = OD
(O is the mid-point of CD)
COM DON
[AAS criteria of congruency]
so, CM = DN (c.p.c.t.) ...(1)
ar (ABC) = ar (ADB)
Question 14:
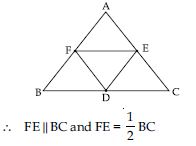
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ABC. Show that BDEF is a parallelogram
Answer:
F is the mid-point of AB and E is the midpoint of AC.
[ Line joining the mid-points of two sides of a triangle is parallel to the third and
half of it.]
or FE || BD
[ BD is the part of BC]
and FE = BD
Now we have
FE || BD and DE || BF
or FE = BD and DE = BF
Therefore BDEF is a parallelogram.
Question 15:
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ABC. Show that
Answer:
BDEF is a parallelogram
ar (BDF) = ar (DEF) ...(1)
[ Diagonal of a || gm divides it in two
triangles of equal area]
DCEF is also parallelogram. [Using same steps as in part (i)]
ar (DEF) = ar (DEC) ...(2)
Also AEDF is a parallelogram
[Using same steps as in part (i)]
ar (AFE) = ar (DEF) ...(3)
From (1), (2) and (3)
ar (DEF) = ar (BDF) = ar (DEC)
= ar (AFE) ...(4)
Now ar (ABC)
= ar (AFE) + ar (BDF) + ar (DEC) + ar (DEF)
...(5)
ar (ABC) = ar (DEF) + ar (DEF) +
ar (DEF)) + ar (DEF)
[Using (4) in (5)]
ar (ABC) = 4 ar (DEF)
or 4 ar (DEF) = ar (ABC)
Question 16:
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ABC. Show that
Answer:
ar (|| gm BDEF) = ar (BDF) + ar (DEF)
= ar (DEF) + ar (DEF)
[Using (4)]
= 2 ar (DEF)
Question 17:
In fig. diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD.
If AB = CD, then show that:
ar (DOC) = ar (AOB)
Answer:
Draw BM AC and DN AC.
In DON and BOM
OD = OB (Given)
∠DNO = ∠BMO
[Each = 90 (By construction)]
∠DON = ∠BOM
(Vertically opp. angles)
DON BOM
[AAS criteria of congruency]
So DN = BM (c.p.c.t.)
Also ar (DON) = ar (BOM) ...(1)
Now in DCN and ABM
∠DNC = ∠BMA
[each angle 90 (by construction)]
CD = AB (Given)
DN = BM (Proved above)
DCN BAM
[RHS criteria of congruency]
ar (DCN) = ar (BAM) ...(2)
Adding (1) and (2), we get
ar (DON) + ar (DCN)
= ar (BOM) + ar (BAM)
ar (DOC) = ar (AOB)
Question 18:
In fig. diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD.
If AB = CD, then show that:
ar (DCB) = ar (ACB)
Answer:
In part (i) we have proved that
ar (DOC) = ar (AOB)
Adding ar (BOC) both sides, we get
ar (DOC) + ar (BOC) = ar (AOB) + ar (BOC)
ar (DCB) = ar (ACB)
Question 19:
In fig. diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD.
If AB = CD, then show that:
DA || CB or ABCD is a parallelogram
Answer:
In part (ii) we have proved that ar (DCB)
= ar (ACB)
Therefore these two triangles in addition to be on the same base CB lie between two same
parallels CB and DA.
So, DA || CB
Now, we have AB = CD and DA || CB
Therefore ABCD is a parallelogram.
Question 20:
D and E are points on sides AB and AC respectively of ABC such that ar (DBC) = ar (EBC). Prove that DE || BC.
Answer:
Given that,
ar (DBC) = ar (EBC)
Two triangles of equal area have common base BC.
Therefore DE || BC
[ Two triangles having same base (or equal bases) and equal areas lie between the same parallels.]
Question 21:
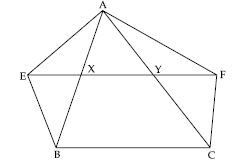
XY is a line parallel to side BC of triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar (ABE) = ar (ACF).
Answer:
ABE and || gm BCYE lie on the same base BE
and between the same parallels BE and AC.
But || gm BCYE and || gm BCFX lie on the same
base BC and between the same parallels
BC and EF.
ar (|| gm BCYE) = ar (|| gm BCFX) ...(3)
From (1), (2) and (3), we get
ar (ABE) = ar (ACF)
Question 22:
The side AB of parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see fig.) Show that ar (ABCD) = ar (PBQR).
Answer:
Given that ABCD and PBQR are parallelograms.
Also CP || AQ.
We observe that
ACQ and APQ lie on the same base AQ and
between the same parallels AQ and CP.
ar (ACQ) = ar (APQ)
Subtracting ar (ABQ) from both sides, we get
ar (ACQ) – ar (ABQ)
= ar (APQ) – ar (ABQ)
ar (ACB) = ar (QPB)
ar (|| gm ABCD) = ar (|| gm PBQR)
Question 23:
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
Answer:
ABD and ABC lie on the same base AB and between the same parallels AB and DC.
ar (ABD) = ar (ABC)
Subtracting ar (AOB) from both sides, we get
ar (ABD) – ar (AOB)
= ar (ABC) – ar (AOB)
ar (AOD) = ar ( BOC) (Proved)
Question 24:
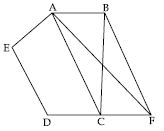
In fig. ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F.
Show that
ar (ACB) = ar (ACF)
Answer:
Given that BF || AC.
ACB and ACF lie on the same base AC and between the same parallels AC and BF.
ar (ACB) = ar ( ACF) ...(1)
Question 25:
In fig. ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F.
Show that
ar (AEDF) = ar (ABCDE)
Answer:
Now
ar (ABCDE) = ar (quad. AEDC) + ar (ABC)
...(2)
= ar (quad. AEDC) + ar (ACF)
[Using (1) in (2)]
= ar (quad. AEDF)
or ar (AEDF) = ar (ABCDE) (Proved)
Question 26:
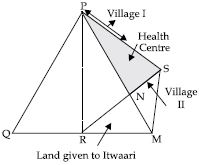
A villager Itwaari has a plot of land of the shape of quadrilateral. The Gram Panchayat of two villages decided to take over some portion of his plot from one of the corners to construct a health centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Answer:
Let Itwaari has land in shape of quadrilateral PQRS.
Draw a line through S parallel to PR, which meets QR produced at M.
Let diagonals PM and RS of new formed quadrilateral intersect each other at point N.
We have PR || SM (By construction)
ar (PRS) = ar (PMR)
[ Triangles on the same base and same parallel
are equal in area]
Subtracting ar (PNR) from both sides, we get
ar (PRS) – ar (PNR)
= ar (PMR) – ar (PNR)
ar (PSN) = ar (MNR)
It implies that Itwaari will give corner triangular shaped plot PSN to the Gram Panchayat
for health centre and will take equal amount of land
(denoted by MNR) adjoining his plot so as to form a triangular plot PQM.
Question 27:
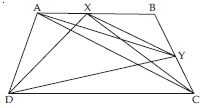
ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y.
Prove that
ar (ADX) = ar (ACY).
Answer:
Join CX. ADX and ACX lie on the same base XA and between the same parallels XA and DC.
ar (ADX) = ar (ACX) ...(1)
Also ACX and ACY lie on the same base AC and between same parallels XY and AC.
ar (ACX) = ar (ACY) ...(2)
From (1) and (2), we get
ar (ADX) = ar (ACY). (Proved)
Question 28:
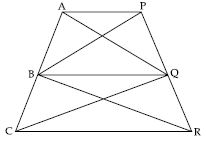
In fig., AP || BQ || CR. Prove that ar (AQC) =ar (PBR).
Answer:
AP and BQ.
ar (ABQ) = ar (BPQ) ...(1)
BQC and BQR lie on the same base BQ and between same parallels BQ and CR.
ar (BQC) = ar (BQR) ...(2)
Adding (1) and (2), we get
ar (ABQ) + ar (BQC)
= ar (BPQ) + ar (BQR)
ar (AQC) = ar (PBR) (Proved)
Question 29:
Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
Answer:
Given that,
ar (AOD) = ar (BOC)
Adding ar (AOB) both sides, we get
ar (AOD) + ar (AOB) = ar (BOC) + ar (AOB)
ar (ABD) = ar (ABC)
As we know that, if two triangles are equal in area, lie on the same base then they lie
between same parallels. We have ABD and ABC lie on common base AB and are equal in area.
They lie in same parallels AB and DC.
or AB || DC.
Now in quad. ABCD we have AB || DC.
So, ABCD is a trapezium.
[ In a trapezium one pair of opposite sides is parallel.]
Question 30:
In fig., ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
Answer:
Given that DRC and DPC lie on the same
base DC
also ar ( DRC) = ar (DPC) ...(1)
DC || RP
[ If two triangles equal in area lie on the
same base then they always lie between same
parallels.]
In quad. DCPR;
DC || RP
So, DCPR is a trapezium.
Also given that
ar (BDP) = ar (ARC) ...(2)
Equation (1) can be written as
ar (DPC) = ar (DRC) ...(3)
Subtracting (3) from (2), we get
ar (BDP) – ar (DPC)
= ar (ARC) – ar (DRC)
ar (BDC) = ar (ADC)
We have BDC and ADC equal in area; lie on common base DC.
AB || DC
[ If two triangles equal in area lie on the same base then they always lie between
same parallels]
Now in quadrilateral ABCD we have
AB || DC
So, ABCD is a trapezium.
Question 31:
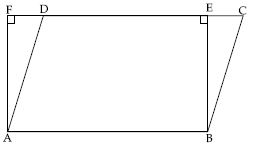
Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
Answer:
Given: Parallelogram ABCD and rectangle ABEF are on same base AB and between the same
parallels AB and CF. Therefore ar (||gm ABCD) = ar (rect. ABEF)
To prove: AB + BC + CD + AD >AB + BE + EF + AF.
Proof: AB = CD
[ Opp. sides of a || gm are always equal]
AB = EF
[ Opp. sides of rect. are always equal]
CD = EF ...(1)
Adding AB to both sides of eq. (1), we get
AB + CD = AB + EF ...(2)
If all the segments that can be drawn to a given line from a point not lying on it,
the segment is the shortest.
BE < BC and AF < AD
or BC > BE
and AD > AF
BC + AD > BE + AF ...(3)
From eq. (2) and (3), we get
AB + BC + CD + AF > AB + BE + EF + AF.
(Proved)
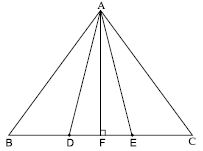
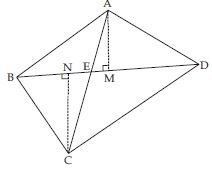
Question 32:
In fig., D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) =
ar (AEC).
Can you now answer the question that you have left in the ‘introduction’ of this chapter,
whether the field of Budhia has been actually divided into three parts of equal area?
Answer:
In ABC; points D and E divides BC in three equal parts such that BD = DE = EC
Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide ABC into n triangles of equal areas.
Question 33:
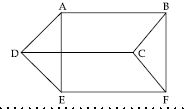
In fig., ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).
Answer:
As we know that opposite sides of a parallelogram are always equal.
In parallelogram ABFE;
AE = BF and AB = EF
In || gm DCFE;
DE = CF and DC = EF
In || gm ABCD;
AD = BC and AB = DC
Now in ADE and BCF,
AE = BF
[Opposite sides of || gm ABFE]
DE = CF
[Opp. sides of || gm DCFE]
and AD = BC
[Opp. sides of || gm of ABCD]
ADE BCF
[SSS criteria of congruency]
So, ar (ADE) = ar (BCF)
[Area of two congruent figures is always equal]
Question 34:
In fig., ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).
Answer:
Join A and C.
APC and BPC are on the same base PC and between the same parallels PC and AB.
ar (APC) = ar (BPC) ... (1)
ABCD is a || gm.
AD = BC
[ Opposite sides of a parallelogram are equal.]
Also BC = CQ (given)
AD = CQ
Now AD || CQ
[ CQ is the extension of BC.]
and AD = CQ
ADQC is a parallelogram.
[ If one pair of opposite sides of a quadrilateral are equal and parallel then it is a
parallelogram.]
Since diagonals of a || gm bisect each other.
AP = PQ and CP = DP
Now in APC and DPQ
AP = PQ (Proved above)
∠APC = ∠DPQ
(Vert. opp. angles)
PC = PD (Proved above)
APC DPQ
ar (APC) = ar (DPQ) ... (2)
[ Area of congruent figures is always equal]
From (1) and (2), we get
ar (BPC) = ar (DPQ) (Proved)
Question 35:
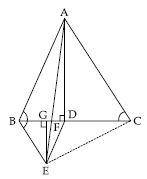
In fig., ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:
Answer:
Join EC and AD.
ABC is an equilateral triangle.
∠BAC = ∠ABC = ∠ACB = 60
BDE is also an equilateral triangle.
∠EBD = ∠BED = ∠BDE = 60
Now if we take two lines.
AC and BE and BC as a transversal.
then ∠EBD = ∠ACB
(each angle 60)
BE || AC
[ When alternate angles are equal then lines are parallel.]
Similarly, for lines AB and DE and BF as transversal.
∠ABC = ∠BDE
(each = 60) [alternate angles]
AB || DE
Question 36:
In fig., ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:
Answer:
Join EC and AD.
ABC is an equilateral triangle.
∠BAC = ∠ABC = ∠ACB = 60
BDE is also an equilateral triangle.
∠EBD = ∠BED = ∠BDE = 60
Now if we take two lines.
AC and BE and BC as a transversal.
then ∠EBD = ∠ACB
(each angle 60)
BE || AC
[ When alternate angles are equal then lines are parallel.]
Similarly, for lines AB and DE and BF as transversal.
∠ABC = ∠BDE
(each = 60) [alternate angles]
AB || DE
In BEC, ED is the median
[ Median divides, the triangle in two triangles having equal area.]
We have BE || AC.
Therefore BEC and BAE are on the same base BE and between the same parallels BE and AC.
ar (BEC) = ar (BAE) ... (4)
Using (4) in (3), we get
Question 37:
In fig., ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:
ar (ABC)= 2 ar (BEC)
Answer:
Join EC and AD.
ABC is an equilateral triangle.
∠BAC = ∠ABC = ∠ACB = 60
BDE is also an equilateral triangle.
∠EBD = ∠BED = ∠BDE = 60
Now if we take two lines.
AC and BE and BC as a transversal.
then ∠EBD = ∠ACB
(each angle 60)
BE || AC
[ When alternate angles are equal then lines are parallel.]
Similarly, for lines AB and DE and BF as transversal.
∠ABC = ∠BDE
(each = 60) [alternate angles]
AB || DE
Question 38:
In fig., ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:
ar (BFE = ar (AFD)
Answer:
Join EC and AD.
ABC is an equilateral triangle.
∠BAC = ∠ABC = ∠ACB = 60
BDE is also an equilateral triangle.
∠EBD = ∠BED = ∠BDE = 60
Now if we take two lines.
AC and BE and BC as a transversal.
then ∠EBD = ∠ACB
(each angle 60)
BE || AC
[ When alternate angles are equal then lines are parallel.]
Similarly, for lines AB and DE and BF as transversal.
∠ABC = ∠BDE
(each = 60) [alternate angles]
AB || DE
BDE and AED are on the same base DE and between same parallels AB and DE.
ar (BDE) = ar (AED)
Subtracting ar (FED) from both sides, we get ar(BDE) – ar(FED) = ar(AED) – ar(FED)
ar (BFE) = ar (AFD) ... (8)
Question 39:
In fig., ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:
ar (BFE) = 2ar (FED)
Answer:
Join EC and AD.
ABC is an equilateral triangle.
∠BAC = ∠ABC = ∠ACB = 60
BDE is also an equilateral triangle.
∠EBD = ∠BED = ∠BDE = 60
Now if we take two lines.
AC and BE and BC as a transversal.
then ∠EBD = ∠ACB
(each angle 60)
BE || AC
[ When alternate angles are equal then lines are parallel.]
Similarly, for lines AB and DE and BF as transversal.
∠ABC = ∠BDE
(each = 60) [alternate angles]
AB || DE
In an equilateral triangle; median drawn is also perpendicular to the side.
AD BC
[ AD is median of ABC]
Question 40:
In fig., ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:
ar (BFE) = 2ar (FED)
Answer:
Join EC and AD.
ABC is an equilateral triangle.
∠BAC = ∠ABC = ∠ACB = 60
BDE is also an equilateral triangle.
∠EBD = ∠BED = ∠BDE = 60
Now if we take two lines.
AC and BE and BC as a transversal.
then ∠EBD = ∠ACB
(each angle 60)
BE || AC
[ When alternate angles are equal then lines are parallel.]
Similarly, for lines AB and DE and BF as transversal.
∠ABC = ∠BDE
(each = 60) [alternate angles]
AB || DE
In an equilateral triangle; median drawn is also perpendicular to the side.
AD BC
[ AD is median of ABC]
Question 41:
In fig., ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:
Answer:
Join EC and AD.
ABC is an equilateral triangle.
∠BAC = ∠ABC = ∠ACB = 60
BDE is also an equilateral triangle.
∠EBD = ∠BED = ∠BDE = 60
Now if we take two lines.
AC and BE and BC as a transversal.
then ∠EBD = ∠ACB
(each angle 60)
BE || AC
[ When alternate angles are equal then lines are parallel.]
Similarly, for lines AB and DE and BF as transversal.
∠ABC = ∠BDE
(each = 60) [alternate angles]
AB || DE
ar (AFC) = ar (AFD) + ar (ADC)
[Using result of part (i)]
= 2 ar (FED) + 2 ar (BDE)
= 2 ar (FED) + 2 ar(AED)
[ BDE and AED are on the same base ED
and between same parallels AB and DE]
= 2 ar (FED) + 2 [ar (AFD) + ar (FED)]
= 2 ar (FED) + 2 ar (AFD) + 2 ar (FED)
= 4 ar (FED) + 2(2 ar (FED)]
[Using result in (11)]
= 4 ar (FED) + 4 ar (FED)
ar (AFC) = 8 ar (FED)
or 8 ar (FED) = ar (AFC)
Question 42:
Diagonals AC and BD of a quadrilateral ABCD intersect each other at E. Show that ar (AEB) × ar (CED) = ar (AED) × ar (BEC).
Answer:
Given: A quadrilateral ABCD, in which diagonals AC and BD intersect each other at point
E.
To prove: ar (AED) × ar (BEC) = ar (ABE) × ar (CDE)
Construction: From A, draw AM BD and from C, draw CN BD.
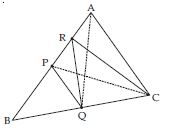
Question 43:
P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
Answer:
Question 44:
P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
Answer:
Question 45:
P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the
mid-point of AP, show that
ar (PBQ) = ar (ARC)
Answer:
Question 46:
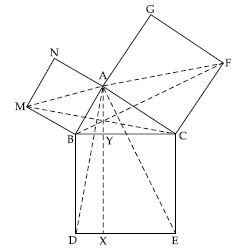
In fig. ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the
sides BC, CA and AB respectively. Line segment AX DE meets BC at Y. Show that:
MBC ABD
Answer:
∠ABM = ∠CBD (Each 90)
Adding ∠ABC both sides, we get
∠ABM + ∠ABC = ∠CBD + ∠ABC
∠MBC = ∠ABD ...(1)
Now in MBC and ABD;
MB = AB
[Equal sides of square ABMN]
BC = BD [Sides of square BCED]
∠MBC = ∠ABD [Proved above]
MBC ABD
[By SAS criteria of congruency]
Question 47:
n fig. ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the
sides BC, CA and AB respectively. Line segment AX DE meets BC at Y. Show that:
ar (BYXD)=2 ar (MBC)
Answer:
From (i), we have
(MBC) ABD
ar (MBC) = ar (ABD)
ar (MBC) = ar (trap ABDX) – ar (ADX)
2ar (MBC) = BD . BY
2ar (MBC) = ar (rect. BYXD)
Hence, ar (BYXD) = 2ar (MBC) (Proved)
Question 48:
n fig. ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the
sides BC, CA and AB respectively. Line segment AX DE meets BC at Y. Show that:
ar (BYXD) =ar (ABMN)
Answer:
Join AM;
ABMN is a square.
NA || MB
AC || MB
Now AMB and MBC are on the same base
MB and between the same parallels MB and AC.
ar (AMB) = ar (MBC) ...(2)
From result (ii), we have
ar (BYXD) = 2ar (MBC) ...(3)
Using (2) in (3), we get
ar (BYXD) = 2ar (AMB)
ar (BYXD) = ar (square ABMN)
[ Diagonal AM of square ABMN divides it in two triangles of equal area] ...(4)
Question 49:
In fig. ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the
sides BC, CA and AB respectively. Line segment AX DE meets BC at Y. Show that:
FCB ACE
Answer:
In FCB and ACE
FC = AC
(Sides of square ACFG)
BC = CE
(Sides of square BCED)
∠BCF = ∠ACE
[ ∠ACF = ∠BCE (Each 90)
∠ACF + ∠ACB = ∠BCE + ∠ACB
∠BCF = ∠ACE]
FCB ACE
(SAS criteria of congruency)
Question 50:
In fig. ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the
sides BC, CA and AB respectively. Line segment AX DE meets BC at Y. Show that:
ar (CYXE)=2 ar (FCB)
Answer:
From (iv) we have
FCB ACE
ar (FCB) = ar (ACE)
ar (FCB) = ar (trap ACEX) – (AEX)
2ar (FCB) = CE . CY
2ar (FCB) = ar (rect. CYXE)
Hence, ar (CYXE) = 2ar (FCB) (Proved)
Question 51:
In fig. ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the
sides BC, CA and AB respectively. Line segment AX DE meets BC at Y. Show that:
ar (CYXE)=ar (ACFG)
Answer:
Join AF;
ACFG is a square
FC || AG
FC || AB
Now ACF and FCB are on the same base FC and between the same parallels FC and AB.
ar (ACF) = ar (FCB) ...(5)
From result (v) we have,
ar (CYXE) = 2ar (FCB) ...(6)
Using (5) in (6), we get
ar (CYXE) = 2ar (ACF)
Diagonal AF of square ACFG divides it in two triangles of equal area.
ar (CYXE) = ar (sq. ACFG) ....(7)
Question 52:
In fig. ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the
sides BC, CA and AB respectively. Line segment AX DE meets BC at Y. Show that:
ar (BCED) = ar (ABMN) + ar (ACFG)
Answer:
ar (BYXD) + ar (CYXE)
= ar (ABMN) + ar (ACFG)
ar (BCED)
= ar (ABMN) + ar (ACFG)