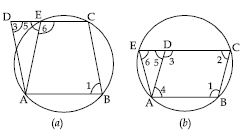
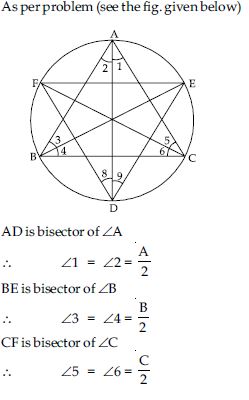
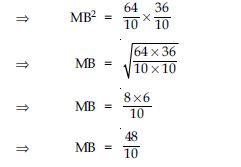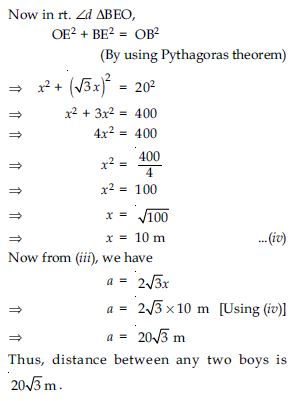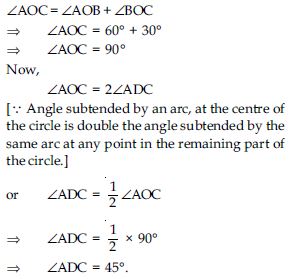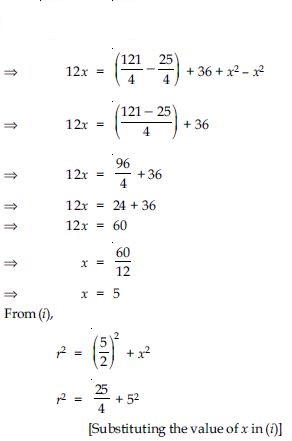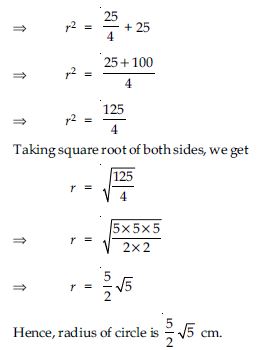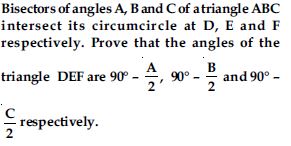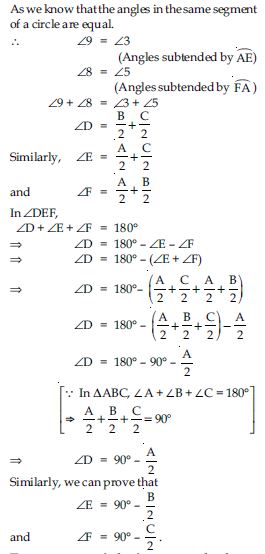Question 1:
The centre of a circle lies in ___________ of the circle. (exterior/interior)
Answer:
interior
Question 2:
A point, whose distance from the centre of a circle is greater than its radius lies in ___________ of the circle. (exterior/interior)
Answer:
exterior
Question 3:
The longest chord of a circle is a ___________ of the circle.
Answer:
diameter
Question 4:
An arc is a ___________ when its ends are the ends of a diameter.
Answer:
semicircle
Question 5:
Segment of a circle is the region between an arc and ___________ of the circle.
Answer:
chord
Question 6:
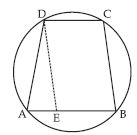
A circle divides the plane, on which it lies, in ___________ parts.
Answer:
three
Question 7:
Line segment joining the centre to any point on the circle is a radius of the circle.
- TRUE
- FALSE
Answer:
TRUE
Question 8:
A circle has only finite number of equal chords.
- TRUE
- FALSE
Answer:
FALSE
Correct statement: A circle has infinite number of equal chords.
Question 9:
If a circle is divided into three equal arcs, each is a major arc.
- TRUE
- FALSE
Answer:
FALSE
Correct statement: If a circle is divided into three equal arcs, each is a minor arc.
Question 10:
A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
- TRUE
- FALSE
Answer:
TRUE
Question 11:
Sector is the region between the chord and its corresponding arc.
- TRUE
- FALSE
Answer:
FALSE
Correct statement: Segment of a circle is the region between the chord and its corresponding
arc.
Question 12:
A circle is a plane figure.
- TRUE
- FALSE
Answer:
TRUE
Question 13:
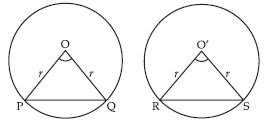
Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Answer:
Two circles are said to be congruent if and only if one of them can be superposed on the
other so as to cover it exactly.
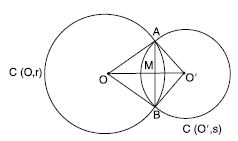
Let C(O, r) and C(O′, s) be two circles. Let us imagine that the circle C(O′, s) is
superposed on C(O, r) so that O′ coincide with O. Then it can easily be seen that C(O′, s)
will cover C(O, r) completely if and only if r = s.
Hence, we can say that two circles are congruent, if and only if, they have equal radii. Now
using this concept we have to prove that equal chords of congruent circles subtended equal
angles at the centre which is proved as follows:
Given: PQ and RS are equal chords of congruent circles
C(O, r) and C′(O′ r).
To prove: ∠POQ = ∠RO′S
Proof: In triangles POQ and RO′S (See fig.)
OP = OQ = O′R = O′S
= r (Radius)
PQ = RS (Given)
POQ RO′S
(By SSS congruency)
∠POQ = ∠RO′S
(Congruent part of congruent triangles)
Question 14:
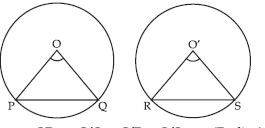
Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Answer:
Given: Two chords PQ and RS of congruent circles C(O, r) and C′(O′, r) such that.
∠POQ = ∠RO′S
To prove: PQ = RS
Proof: In triangle POQ and RO′S (see fig.)
OP = O′Q = O′R = O′S = r (Radius)
∠POQ = ∠RO′S (Given)
POQ RO′S
(By SAS congruency)
PQ = RS
(Congruent parts of congruent triangles)
Question 15:
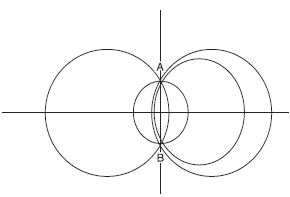
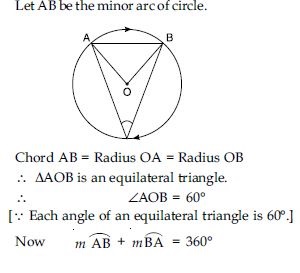
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Answer:
From the fig. we observe that when different pair of circles are drawn; each pair have two
points (say A and B) in common.
Maximum number of common points are two. Suppose that two circles C(O, r) and C(O′, s)
intersect each other in three points, say A, B and C.
Then A, B and C are non-collinear points.
We know that:
There is one and only one circle passing through three non-collinear points.
Therefore a unique circle passes through A, B and C.
O′ coincides with O and s = r
A contradiction to the fact that
C(O′, s) C(O, r)
Our supposition is wrong.
Hence, two different circles cannot intersect each other at more than two points.
Question 16:
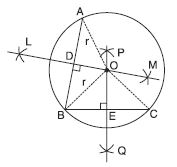
Suppose you are given a circle. Give a construction to find its centre.
Answer:
Steps of construction:
(i) Take any three points A, B and C on the circle.
(ii) Join AB and BC.
(iii) Draw perpendicular bisector say LM on AB.
(iv) Draw perpendicular bisector PQ on BC.
(v) Let LM and PQ intersect at the point O.
Then O is the centre of the circle.
Verification:
O lies on the perpendicular bisector of AB.
OA = OB ... (i)
O lies on the perpendicular bisector of BC.
OB = OC ... (ii)
From (i) and (ii) we observe that
OA = OB = OC = r (say)
Three non collinear points A, B and C are at equal distance (r) from the point O inside the
circle.
Hence, O is the centre of the circle.
Question 17:
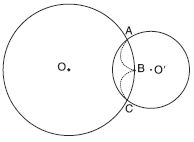
If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Answer:
Proof: C(O, r) and C(O′, s) be two circles intersecting A and B. To prove OO′ is the
perpendicular bisector of the chord AB. Draw line segments OA, OB, O′A and O′B (See
fig.)
In triangles OAO′ and OBO′,
OA = OB = r
O′A = O′B = s
and OO′ = OO′
OAO′ OBO′ (By SSS congruency)
∠AOO′ = ∠BOO′
Let M be the point of intersection of AB and
OO′. Then in triangles AOM and BOM,
OA = OB
∠AOM = ∠BOM
( ∠AOO′ = ∠AOM and ∠BOO′ = ∠BOM)
and OM = OM
AOM BOM (By SAS axiom)
AM = MB ... (i)
and ∠AMO = ∠BMO ... (ii)
Now ∠AMO + ∠BMO = 180
(Linear pair axiom)
∠AMO + ∠AMO = 180
2∠AMO = 180
∠AMO = 90
Also ∠BMO = 90 (∠AMO = ∠BMO)
Now, we have
AM = MB
∠AMO = ∠BMO = 90
It proves that line OO′ joining centres O and
O′ lies on the perpendicular bisector of common chord AB.
Question 18:
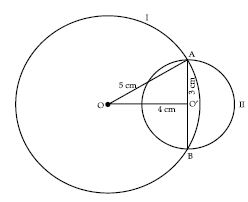
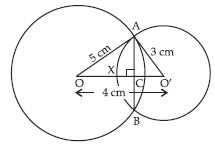
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Answer:
Let two circles with centres O and O′ intersect each other at points A and B. On joining A and B; AB is the common chord.
Radius OA = 5 cm, Radius O′A = 3 cm, distance between their centres OO′ = 4 cm.
We observe that in triangle AOO′;
52 = 42 + 32
25 = 16 + 9
25 = 25
Pythagoras result, holds in AO′O.
Hence, AO′O is rt. ∠d triangle, rt. angle at O′.
As we know that perpendicular drawn from the centre of the circle bisects the chord.
Hence, O′ is the mid-point of the chord AB.
Also O′ is the centre of the circle II.
Therefore, length of chord AB = Diameter of circle II
Length of chord AB = 2 × 3 cm = 6 cm.
ALITER
Let two circles with centre O and O′ intersect
each other at points A and B. Let common chord
AB intersects OO′ at point C.
Let OC = x cm
O′C = 4 – x cm
As we know that line joining the centres of two circles is perpendicular bisector of the
common chord of circles.
In rt. ∠d OCA,
AC2 + OC2 = OA2
[Using Pythagoras Theorem]
AC2 + x2 = 52
AC2 = 25 – x2 ...(i)
Similarly in ACO′,
AC2 + O′C2 = AO′2
AC2 + (4 – x)2 = 32
AC2 = 9 – (4 – x)2 ...(ii)
From (i) and (ii), we get
25 – x2 = 9 – (4 – x)2
25 – x2 = 9 – (16 + x2 – 8x)
25 – x2 = 9 – 16 – x2 + 8x
– 8x = 9 – 16 – 25 – x2 + x2
– 8x = – 32
x = 4
CO′ = 4 – x
CO′ = 4 – 4
CO′ = 0
It means that O′coincides with C.
AC = Radius, AO′ = 3 cm.
Length of chord AB = Diameter of circle with
centre O′
Length of chord AB = 2 × AO′
= 2 × AC
= 2 × 3 = 6 cm.
Question 19:
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Answer:
Let AB and CD are two equal chords of a circle of centre O intersecting each other at point E
within the circle.
We have to prove that:
(a) AE = CE
(b) BE = DE.
Construction: Draw OM ⊥ AB, ON ⊥ CD also join OE.
Proof: In rt.∠d OME and ONE,
∠OME = ∠ONE (Each 90)
OM = ON
[Equal chords are equidistant from the centre]
hyp. OE = hyp. OE (Common)
OME ONE
[By RHS congruency]
ME = NE
(Congruent parts of congruent triangles) ...(i)
Now; O is the centre of circle and
OM ⊥ AB
But AB = CD (Given)
From (ii) and (iii), we get
AM = NC ...(iv)
Also MB = DN ...(v)
Adding (i) and (iv), we get
AM + ME = NC + NE
AE = CE Proved part (a)
Now, AB = CD (Given)
AE = CE (Proved above)
AB – AE = CD – CE
BE = DE Proved part (b)
Question 20:
If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chord.
Answer:
AB and CD be two equal chords of a circle with centre O intersecting each other with in the
circle at point E. OE is joined. We have to prove that
∠OEM = ∠OEN.
Construction: Draw OM ⊥ AB,
ON ⊥ CD.
Proof: In rt. ∠d OME and ONE,
∠OME = ∠ONE (Each 90)
OM = ON
(Equal chords are equidistant from the centre)
Hyp. OE = Hyp. OE (Common)
OME ONE
(By RHS congruency)
∠OEM = ∠OEN
(Congruent parts of congruent triangles)
Question 21:
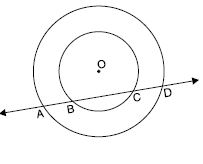
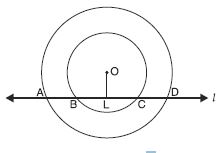
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (See fig.).
Answer:
Line l intersects two concentric circles with centre O at points A, B, C and D.
We have to prove that
AB = CD
Construction: Draw OL ⊥ l.
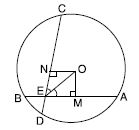
Proof: AD is a chord of outer circle and OL ⊥ AD.
AL = LD
[ Perpendicular drawn from the centre bisects the chord] ...(i)
Now, BC is a chord of inner circle and OL ⊥ BC.
BL = LC
[Same reason as above] ...(ii)
Subtracting (ii) from (i), we get
AL – BL = LD – LC
AB = CD (Proved
Question 22:
Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5 m
drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma.
If the distance between Reshma and Salma and between Salma and Mandip is 6 m each, what is
the distance between Reshma and Mandip?
Answer:
Let position of Reshma, Salma and Mandip is denoted by points A, B and C.
Given that the distance between Reshma and Salma is 6 m and distance between Salma and
Mandip is 6 m. It means:
AB = BC = 6 m
Centre lies on the bisector of ∠BAC.
Let M be the point of intersection of BC and OA.
Again, since AB = BC
and AM bisects ∠CAB
AM ⊥ CB and M is the mid-point of CB.
Let OM = x
then MA = 5 – x
Now, from right-angled OMB,
OB2 = OM2 + MB2
52 = x2 + MB2 ...(1)
MB = 4.8 m
BC = 2MB = 2 × 4.8 = 9.6 m
Hence, distance between Reshma and Mandip is 9.6 m.
Question 23:
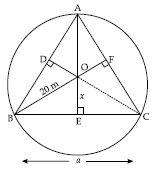
A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
Answer:
Let position of three boys Ankur, Syed and David is denoted by points A, B and C.
Three points are at equal distances.
AB = BC = AC = a m (say)
Equal sides of equilateral triangles are as equal chords and perpendicular distances of equal
chords of a circle are equidistant from the centre.
OD = OE = OF = x m (say)
Join OA, OB and OC.
Now, we have three congruent triangles,
OAB, OBC and AOC
area (AOB) = area (BOC)
= area (AOC) ...(i)
Now area of equilateral
triangle ABC of side a = ar (AOB)
+ ar (BOC) + ar (AOC) ...(ii)
Area (ABC) = 3Area (BOC)
[Using (i) in (ii)]
Question 24:
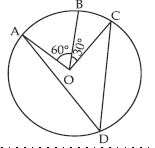
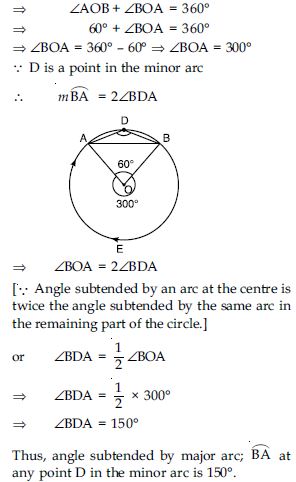
In fig. A, B, C are three points on a circle with centre O such that ∠BOC = 30, ∠AOB = 60.
If D is a point on the circle other than the arc
ABC, find ∠ADC.
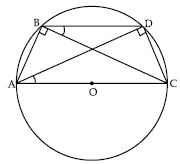
Answer:
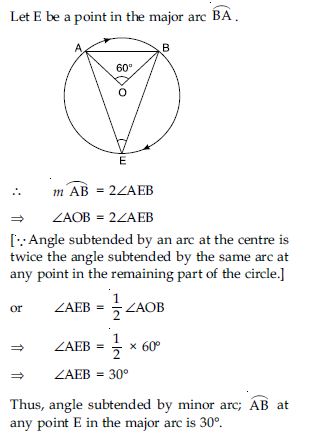
Question 25:
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord on a point on the minor arc and also at a point on the major arc.
Answer:
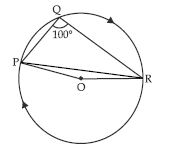
Question 26:
In fig., ∠PQR = 100, where P, Q, R are points on a circle with centre O. Find ∠OPR.
Answer:
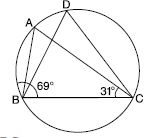
Question 27:
In fig., ∠ABC = 69, ∠ACB = 31, find ∠BDC.
∠BAC + ∠ABC + ∠ACB = 180
Answer:
In ABC ;
∠BAC + 69 + 31 = 180
∠BAC = 180 – 69 – 31
∠BAC = 80 ... (i)
A and D are the points in the same segment of circle
Therefore ∠BDC = ∠BAC
[ Angles subtended by the same arc at any points in the alternate segment of a circle
are equal.]
∠BDC = 80 [Using (i)]
Question 28:
In fig., A, B, C and D are four points on a circle.
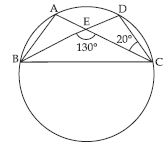
AC and BD intersect at a point E such that ∠BEC = 130 and ∠ECD = 20. Find ∠BAC.
Answer:
According to fig.,
∠CED + ∠BEC = 180 (Linear pair)
∠CED + 130 = 180
∠CED = 180 – 130
∠CED = 50 ... (i)
∠AEB = ∠CED
(Vertically opp. angles)
∠AEB = 50 [Using (i)]
Now,
∠ABD = ∠ACD
[Angles subtended by the arc AD in the same segment of a circle are equal]
∠ABD = 20
[ ∠ACD = 20 (Given)]
Now in AEB;
∠BAE + ∠ABE + ∠AEB = 180
[Angle sum property of a triangle]
∠BAE + 20 + 50 = 180
∠BAE = 180 – 20 – 50
∠BAE = 110
or ∠BAE = 110
Question 29:
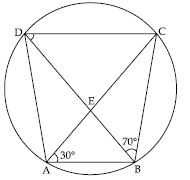
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. ∠DBC = 70, ∠BAC is 30, find ∠BCD. Further, if AB = BC, find ∠ECD.
Answer:
∠BDC = ∠BAC [Angles of the same segment]
∠BDC = 30
( ∠BAC = 30)
In BCD;
∠BCD + ∠DBC + ∠BDC = 180
∠BCD + 70 + 30 = 180
[∠DBC = 70]
∠BCD = 180 – 70 – 30
∠BCD = 80 ... (i)
If AB = BC
Then in ABC;
∠ACB = ∠BAC
(Angles opp. to equal sides of a triangle are equal)
∠ACB = 30 ... (ii)
Now,
∠BCD = ∠ACB + ∠ACD
80 = 30 + ∠ACD
[Using (i) and (ii)]
80 – 30 = ∠ACD
50 = ∠ACD
or ∠ACD = 50
or ∠ECD = 50
Question 30:
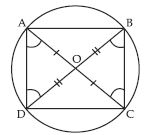
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Answer:
AC is the diameter
∠B = ∠D = 90 ... (1)
(Angle is a semicircle is right angle)
Similarly, BD is the diameter
AD = BC
(Chords opposite to equal arcs) ... (3)
Similarly, AB = DC ... (4)
From (1), (2), (3) and (4) we observe that each angle of the quadrilateral is 90 and opposite sides are equal.
Hence, ABCD is a rectangle.
Question 31:
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Answer:
Given: A trapezium ABCD in which AB CD and AD = BC.
To prove: The points A, B, C and D are concyclic, (i.e., trapezium ABCD is cyclic).
Construction: Draw DE II CB.
Proof: DE II CB and EB II DC.
EBCD is a IIgm
DE = CB and ∠DEB = ∠DCB.
Opposite ∠s of a IIgm are equal.
Now, AD = BC and BC = DE
DA = DE ∠DAE = ∠DEA.
[ Angles opposite to equal sides in a
triangle are equal]
But ∠DEA + ∠DEB = 180
... (Linear pair)
∠DAE + ∠DCB = 180
[ ∠DEA = ∠DAE & ∠DEB = ∠DCB
(Proved above)]
∠DAB + ∠DCB = 180 ....(1)
∠A + ∠C = 180
Hence, ABCD is a cyclic trapezium.
[ Opposite angles of a cyclic quadrilateral are supplementary, as in Result (1)].
Question 32:
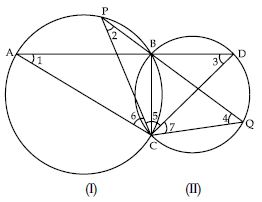
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see fig.). Prove that ∠ACP = ∠QCD.
Answer:
Arc BC of circle I subtends ∠1 and ∠2 in the
same segment of circle.
∠1 = ∠2
[Angles subtended by the same arc in the alternate segment of a circle are equal]
Arc BC of circle II subtends ∠3 and ∠4 in the
same segment of a circle.
∠3 = ∠4
[same reason as above]
Now in ACD,
∠A + ∠C + ∠D = 180
[Angle sum property of a triangle]
∠1 + ∠5 + ∠6 + ∠3 = 180 ... (i)
In PCQ;
∠P + ∠C + ∠Q = 180
[Angle sum property of a triangle]
∠2 + ∠5 + ∠7 + ∠4 = 180 ... (ii)
From (i) and (ii),
∠1 + ∠5 + ∠6 + ∠3 = ∠2 + ∠5 + ∠7 + ∠4
... (iii)
But ∠1 = ∠2 and ∠3 = ∠4
(Proved above)
From (iii), we get
∠1 + ∠5 + ∠6 + ∠3 = ∠1 + ∠5 + ∠7 + ∠3
∠6 = ∠7
or ∠ACP = ∠QCD [Hence proved]
Question 33:
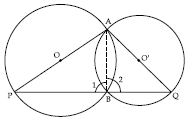
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Answer:
Given: Two circles intersect each other at points A and B. AP and AQ be their respective diameters.
To prove: Point B lies on the third side PQ.
Construction: Join A and B.
Proof: AP is a diameter.
∠1 = 90 (Angle in a semicircle)
Also AQ is a diameter.
∠2 = 90 (Angle in a semicircle)
∠1 + ∠2 = 90 + 90
∠PBQ = 180
PBQ is a line.
Thus, B (the point of intersection of these circles) lies on the third side i.e., on PQ.
Question 34:
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Answer:
We have ABC and ADC two right triangles rt.
angled at B and D respectively.
∠ABC = ∠ADC (Each 90)
If we draw a circle with AC (the common hypotenuse) as diameter, this circle will definitely
passes through points B and D.
[Because B and D are the points in the alternate segment of an arc AC.]
Question 35:
Prove that a cyclic parallelogram is a rectangle.
Answer:
Let ABCD be a cyclic parallelogram. To prove that it is a rectangle, it is sufficient to show that one of the angles of parallelogram ABCD is a right angle.
Now ABCD is a parallelogram.
∠B = ∠D ... (i)
[ Opposite angles of a gm are equal]
Also, ABCD is a cyclic quadrilateral.
∠B + ∠D = 180 ... (ii)
From (i) and (ii), we get:
∠B + ∠B = 180
2∠B = 180
∠B = 90
Thus, ∠B = ∠D = 90
Hence, ABCD is a rectangle.
Question 36:
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Answer:
Let two circles with respective centres A and B intersect each other at points C and D.
We have to prove ∠ACB = ∠ADB
AC = AD (each radii)
BC = BD (each radii)
AB = AB (common)
ABC ABD (By SSS of congruency)
∠ACB = ∠ADB
(Congruent parts of congruent triangles)
Question 37:
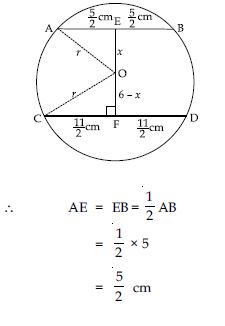
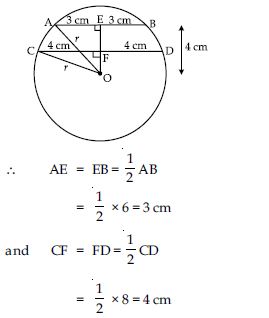
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
Answer:
Let O be the centre of circle.
Join OA and OC.
Since perpendicular from the centre of the circle to the chord bisects the chord.
Question 38:
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
Answer:
Let AB = 6 cm and CD = 8 cm are the chords of circle with centre O.
Join OA and OC.
Since perpendicular from the centre of the circle to the chord bisects the chord.
Perpendicular distance of chord AB from the centre O is OE.
OE = 4 cm
Now in rt. ∠d AOE
OA2 = AE2 + OE2
[Using Pythagoras result]
r2 = 32 + 42
r2 = 9 + 16
r2 = 25
Question 39:
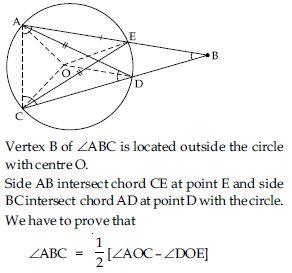
Let vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Answer:
Join OA, OC, OE and OD.
Now, ∠AOC = 2∠AEC
[Angle subtended by an arc at the centre of the circle is twice the angle subtended by the
same arc at any point in the alternate segment of circle.]
Question 40:
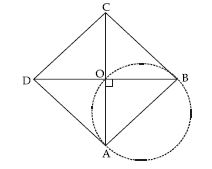
Prove that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
Answer:
Let ABCD be a rhombus in which diagonals AC and BD intersect each other at point O.
As we know that diagonals of a rhombus bisect and perpendicular to each other.
∠AOB = 90
and if we draw a circle with side AB as diameter; it will definitely pass through point O
(the point of intersection of diagonals) because then ∠AOB = 90 will be the angle in a semicircle.
Question 41:
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
Answer:
ABCD is a parallelogram
∠1 = ∠3 ...(i)
(Opposite angles of a parallelogram)
ABCE is a cyclic quadrilateral
∠1 + ∠6 = 180 ...(ii)
∠5 + ∠6 = 180 (Linear pair) ...(iii)
From (ii) and (iii),
∠1 = ∠5 ...(iv)
Now, from (i) and (iv)
∠3 = ∠5
Now in AED,
∠3 = ∠5
AE = AD
( Sides opposite to equal angles in a triangle
are equal)
In fig. (b),
ABCD is a || gm.
∠1 = ∠3
(Opposite angles of a ||gm)
∠2 = ∠4
Also AB CD and BC meets them
∠1 + ∠2 = 180 ...(1)
And AD BC and EC meets them
∠5 = ∠2 (Corr. ∠s) ...(2)
ABCE is cyclic
∠1 + ∠6 = 180 ...(3)
From (1) & (3), we get
∠1 + ∠2 = ∠1 + ∠6
∠2 = ∠6
But from (2),
∠2 = ∠5
∠5 = ∠6
Now in AED,
∠5 = ∠6
AE = AD (Q.E.D.)
Hence, in both the cases,
AE = AD.
Question 42:
AC and BD are chords of a circle which bisect each other. Prove that:
(i) AC and BD are diameters.
(ii) ABCD is a rectangle.
Answer:
Let chords AC and BD of a circle bisect each other at O.
Then OA = OC and OB = OD.
We have to prove that (i) AC and BD are the
diameters. In other words, O is the centre of circle.
AD = BC
[Chords corresponding to the equal arcs]
...(3)
Similarly, AB = DC ...(4)
From (1), (2), (3) and (4) we observe that each angle of the quadrilateral is 90 and opposite sides are equal.
Hence, ABCD is a rectangle.
Question 43:
Answer:
Question 44:
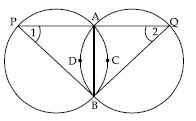
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Answer:
Given: Two equal circles intersect in A and B.
A straight line through A meets the circles in P and Q.
To prove: BP = BQ
Construction: Join A and B.
Proof: AB is a common chord and the circles are equal.
Arcs about the common chord are equal, i.e.,
Since equal arcs of two equal circles subtend equal angles at any point on the remaining part
of the circle,
then, we have
∠1 = ∠2
In PBQ, we have
∠1 = ∠2 (Proved)
Sides opposite to equal angles of a triangle are equal.
Then, we have
BP = BQ.
Question 45:
In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
Answer:
Given that ABC is a triangle and a circle passes through its vertices.
Angle bisector of ∠A and the perpendicular bisector (say l) of its opposite side BC intersect
each other at a point P (say).
We have to prove that circumcircle of ABC also passes through point P.
Proof: As we know that any point on the perpendicular bisector is equidistant from the end
points of the corresponding side,
BP = PC ...(i)
Also we have ∠1 = ∠2
[ AP is the bisector of ∠A (given)] ...(ii)
From (i) and (ii) we observed that equal line segments are subtending equal angles in the
same segment (i.e., at point A) of circumcircle of ABC. Therefore BP and PC acts as chords of circumcircle of ABC and the corresponding