Question 1:
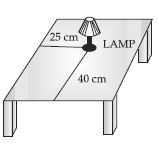
How will you describe the position of a table lamp on your study table to another person?
Answer:
Consider the lamp as a point and table as a plane. Choose any two perpendicular edges of the table. Measure the distance of the lamp from the longer edge. Suppose it is 40 cm. Again, measure the distance of the lamp from the shorter edge, and suppose it is 25 cm. You can write the position of the lamp as (40, 25) or (25, 40), depending on the order fixed by you.
Question 2:
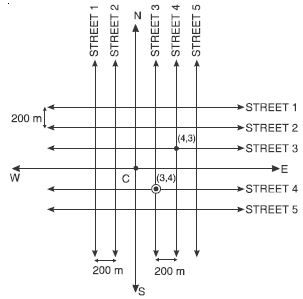
(Street Plan): A city has two main roads which cross each other at the centre of the city.
These two roads are along the North-South direction and East-West direction. All the other
streets of the city run parallel to these roads and are 200 m apart. There are about 5
streets in each direction. Using 1 cm = 200 m, draw a model of the city on your notebook.
Represent roads/streets by single lines.
There are many cross-streets in your model. A particular cross-street is made by two
streets, one running in the North – South direction and another in the East – West
direction. Each cross street is referred to in the following manner: If the 2nd street
running in the North – South direction and 5th in the East – West direction meet at some
crossing, then we will call this cross-street (2, 5). Using this convention find:
(i) how many cross-streets can be referred to as (4, 3)?
(ii) how many cross-streets can be referred to as (3, 4)?
Answer:
The street plan is shown in figure given below:
To reach at cross-street referred as (4, 3); we choose 4th street running in the North-South
direction and 3rd street running in the East- West direction. Then the cross-street referred
as (4, 3) is marked by a dot •; as shown in the above figure.
Similarly the cross-street referred as (3, 4) is marked by •.
We observe that both cross streets are uniquely found because of two reference lines
we have used for locating them.
Question 3:
Write the answer of each of the following questions:
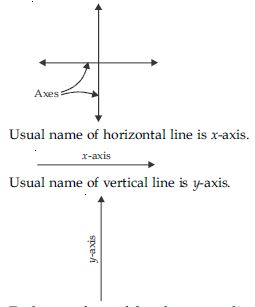
What is the name of horizontal and vertical lines drawn to determine the position of any
point in the cartesian plane?
Answer:
Horizontal and vertical lines which divide the plane into four parts are called axes.
Question 4:
Write the answer of each of the following questions:
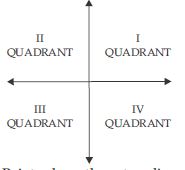
What is the name of each part of the plane formed by horizontal and vertical lines?
Answer:
Each part formed by these two lines (horizontal and vertical lines) is called quadrant.
Question 5:
Write the answer of each of the following questions:
Write the name of the point where horizontal and vertical lines intersect.
Answer:
Point where these two lines intersect is called origin.
Question 6:
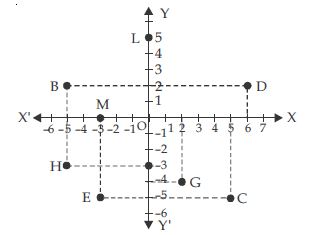
See fig. and write the following:
(i) The coordinates of B.
(ii) The coordinates of C.
(iii) The point identified by the coordinates (–3, –5).
(iv) The point identified by the coordinates (2, –4).
(v) The abscissa of the point D.
(vi) The ordinate of the point H.
(vii) The coordinates of the point L.
(viii) The coordinates of the point M.
Answer:
(i) To reach at point B; we move 5 units left of origin then 2 units up.
In other words, x-coordinate of B is –5 and y–coordinate is 2.
Therefore, coordinates of B are (–5, 2).
(ii) To locate point C; we move 5 units right of the origin then 5 units down. In other
words, x-coordinate of C is 5 and y coordinate is –5.
Therefore, coordinates of C are (5, –5).
(iii) Co-ordinates (–3, –5) are identified by the point E.
(iv) Co-ordinates (2, –4) are identified by the point G.
(v) Co-ordinates of point D are (6, 0) and hence abscissa i.e. x-coordinate of the point D
is 6.
(vi) Ordinate i.e. y-coordinate of the point H is –3.
(vii) To reach at the point L; we move 5 units up on vertical line from origin. In other
words, x-coordinate of L is 0 and y coordinate is 5. Therefore, coordinates of L are (0,
5).
(viii) To locate the point M we move 3 units left on horizontal line from the origin. In
other words, x-coordinate of M is –3 and y coordinate is 0. Therefore, coordinates of M are
(–3, 0).
Question 7:
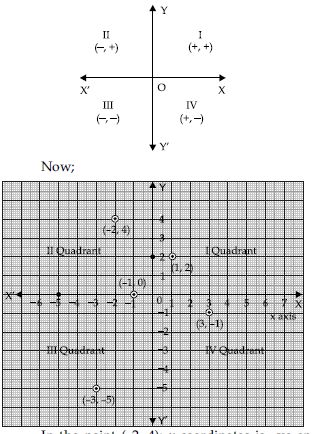
In which quadrant or on which axis do each of the points (–2, 4), (3, –1), (–1, 0), (1, 2) and (–3, –5) lie? Verify your answer by locating them on the Cartesian plane.
Answer:
We locate the quadrants or axes corresponding to the given points with the help of following:
In the point (–2, 4); x-coordinates is –ve and y-coordinate is +ve. Therefore, point (–2, 4)
lies in the II quadrant. In the point (3, –1); x-coordinate is +ve and y–coordinate is
–ve.
Therefore, point (3, –1) lies in the IV quadrant. In the point (–1, 0); x-coordinate is –ve
and y–coordinate is 0.
Therefore, point (–1, 0) lies on the negative x-axis.
In the point (1, 2); x-coordinate is +ve and y–coordinate is +ve.
Therefore, point (1, 2) lies in the I quadrant.
In the point (–3, –5); x–coordinate is –ve and y–coordinate is –ve.
Therefore, point (–3, –5) lies in the III quadrant.
Question 8:
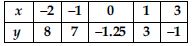
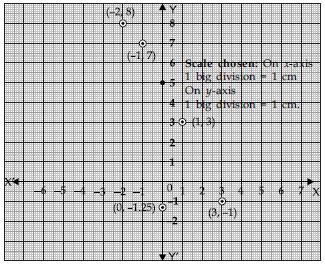
Plot the points (x, y) given in the following table on the plane, choosing suitable units of distance on the axes.
Answer:
Points given in the table are plotted in the graph as follows: