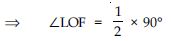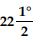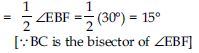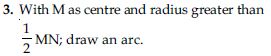Question 1:
Construct an angle of 90 at the initial point of a given ray and justify the construction.
Answer:
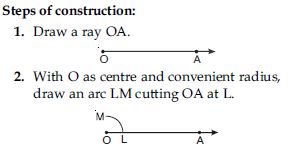
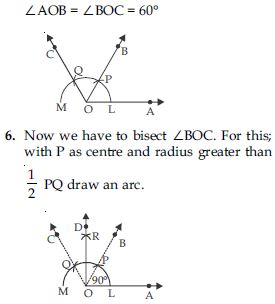
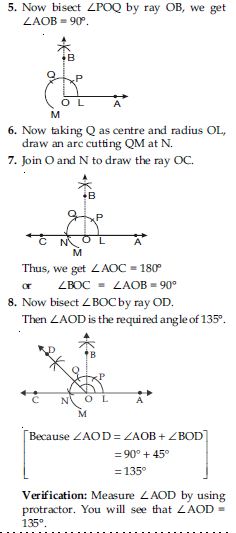
7. Now with Q as centre and the same radius as in step 6, draw another arc cutting the arc
drawn in step 6 at R.
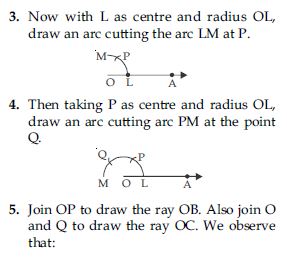
8. Join O and R and draw ray OD. Then ∠AOD is the required angle of 90. Verification: Measure ∠AOD, you will see
that ∠AOD = 90.
Justification of construction:
Join PL, then
OL = OP = PL (By construction)
Therefore, OPL is an equilateral triangle and ∠POL which is same as ∠BOA is equal to 60.
Question 2:
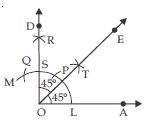
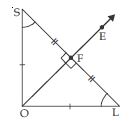
Construct an angle of 45 at the initial point of a given ray and justify the construction.
Answer:
3. Now, with S as centre and the same radius as in step 2, draw another arc cutting the arc drawn in step 2 at T.
4. Join O and T and draw ray OE.
Thus, OE bisects ∠AOD, and therefore, ∠AOE = ∠DOE = 45.
Verification: Measure ∠AOE, you will see that ∠AOE = 45.
Justification of construction:
Join LS, then OLS is an isosceles right triangle, rt. angled at O.
OL = OS
Therefore, O lies on the perpendicular bisector of SL.
SF = FL
and ∠OFS = ∠OFL [Each 90]
Now in OFS and OFL
OF = OF [Common]
OS = OL [By Construction]
SF = FL [Proved above]
OFS OFL [By SSS rule]
∠SOF = ∠LOF (c.p.c.t.)
Now
∠SOF + ∠LOF = ∠SOL
∠LOF + ∠LOF = 90 [from above]
2∠LOF = 90
∠LOF = 45
or ∠AOE = 45
(Which is true according to construction.)
Question 3:
Construct the angles of the following measurements:
30
Answer:
Question 4:
Construct the angles of the following measurements:
Answer:
Question 5:
Construct the angles of the following measurements:
15
Answer:
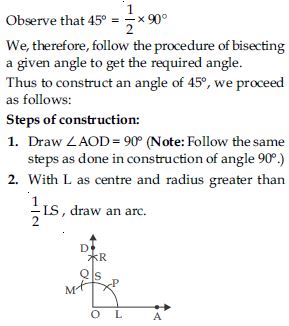
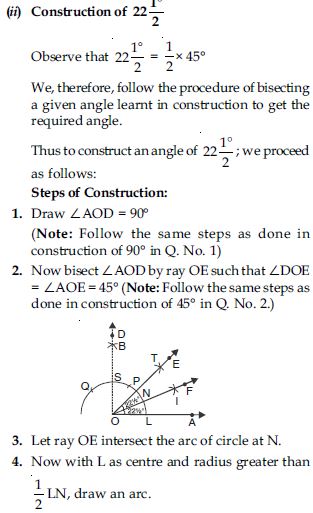
Construction of 15
We, therefore, follow the steps of bisecting a given angle learnt in construction to get the
required angle.
Thus to construct an angle of 15, we proceed as follows:
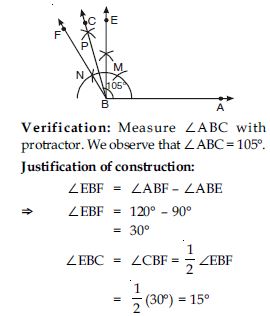
Steps of construction:
1. Draw ∠AOB = 60.
2. Now bisect ∠AOB by ray OC such that ∠BOC = ∠AOC = 30 [Note: Follow the same steps as done in construction of 30 in Q. No. 3 part (i).]
5. With Q as centre and same radius as in step 4; draw another arc cutting the arc drawn in
step 4 at R.
6. Join O and R and draw ray OS.
Thus OS bisects ∠AOC, and therefore, ∠COS = ∠AOS = 15
Verification: Measure ∠AOS with protractor.
We observe that ∠AOS = 15.
Question 6:
Construct the following angles and verify by measuring them by a protractor:
75
Answer:
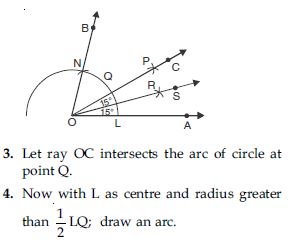
Construction of 75
Steps of construction:
1. Draw ∠ABE = 60 and ∠ABF = 90
(Note: Follow the same steps as done in Example 1 and Question No. 1.)
2. Let ray BF intersects the arc of circle at G.
4. With G as centre and with same radius as in step 3; draw an arc which intersects the
previous arc at point H.
5. Draw a ray BC passing through H which bisects ∠EBF.
Thus ∠ABC = 75 is the required angle.
Verification: Measure ∠ABC with protractor. We observe that ∠ABC = 75.
Justification of construction:
∠EBF = ∠ABF – ∠ABE
= 90 – 60 = 30
∠EBC = ∠CBF
∠ABC = ∠ABE + ∠EBC
= 60 + 15
∠ABC = 75
(Which is true when measured with protractor.)
Question 7:
Construct the following angles and verify by measuring them by a protractor:
105
Answer:
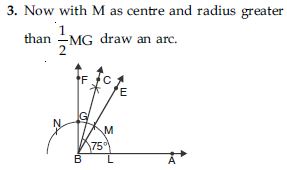
Construction of 105
Steps of construction:
1. Draw ∠ABE = 90 and ∠ABF = 120
2. Let ray BE intersects the arc of circle at M and ray BF intersect the arc of circle at N.
4. With N as centre and with same radius as in step 3, draw another arc which intersects the
previous arc at P.
5. Draw a ray BC passing through P which bisects ∠EBF.
Thus ∠ABC = 105 is the required angle.
[ BC is the bisector of ∠EBF.]
∠ABC = ∠ABE + ∠EBC
= 90 + 15
∠ABC = 105
[Which is true when measured with protractor.]
Question 8:
Construct the following angles and verify by measuring them by a protractor:
135
Answer:
Question 9:
Construct an equilateral triangle, given its side and justify the construction.
Answer:
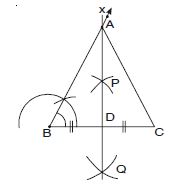
Construction of an equilateral triangle of given side (Let it be ABC whose each side is 6 cm).
Steps of construction:
1. Draw a line segment BC of length 6 cm.
2. At B draw ∠XBC = 60.
3. Draw perpendicular bisector PQ of line segment BC.
4. Let A and D be the points where PQ intersects the ray BX and side BC
respectively.
5. Join AC.
Thus ABC is the required equilateral triangle.
Justification of construction:
In rt. ADB and rt. ADC,
AD = AD (Common)
∠ADB = ∠ADC (each 90)
(by construction)
BD = CD (By construction)
ADB ADC
(By SAS rule of congruency)
∠B = ∠C = 60 (By C.P.C.T.)
Therefore in ABC third angle;
∠A = 180 – (∠B + ∠C)
= 180 – (60 + 60)
= 180 – 120
= 60
Each of three angles of a triangle is 60.
Hence constructed triangle is an equilateral triangle.
Question 10:
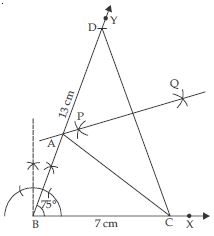
Construct a triangle ABC in which BC = 7 cm, ∠B = 75 and AB + AC = 13 cm.
Answer:
Given: Base BC = 7 cm, ∠B = 75 and sum of two sides AB + AC = 13 cm.
Required: To construct ABC.
Steps of construction:
1. Draw a ray BX and cut off a line segment BC = 7 cm from it.
2. At B; construct ∠YBX = 75.
3. With B as centre and radius = 13 cm (_ AB + AC = 13 cm) draw an arc to meet BY at D.
4. Join CD.
5. Draw perpendicular bisector PQ of CD intersecting BD at A.
6. Join AC.
Then ABC is the required triangle.
A lies on perpendicular bisector of CD.
AC = AD and then
AB = BD – AD
AB = BD – AC
AB + AC = BD = 13 cm
(Which is true as given)
Question 11:
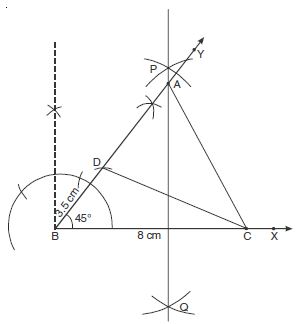
Construct a triangle ABC in which BC = 8 cm, ∠B = 45 and AB – AC = 3.5 cm.
Answer:
Given: Base BC = 8 cm,
∠B = 45
and difference of two sides;
AB – AC = 3.5 cm
Required: To construct ABC.
Steps of construction:
1. Draw a ray BX and cut off a line segment BC = 8 cm from it.
2. Cut ∠YBC = 45.
3. Cut off a line segment BD = 3.5 cm
( AB – AC = 3.5 cm) from BY.
4. Join CD.
5. Draw perpendicular bisector PQ of CD intersecting BY at a point A.
6. Join AC.
Then ABC is the required triangle.
A lies on the perpendicular bisector of CD.
AD = AC
Now BD = AB – AD
BD = AB – AC
BD = AB – AC = 3.5 cm
(Which is true as given)
Question 12:
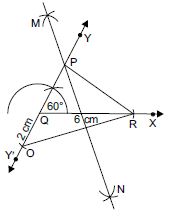
Construct a triangle PQR in which QR = 6 cm, ∠Q = 60 and PR – PQ = 2 cm.
Answer:
Given: Base QR = 6 cm; one base angle; ∠Q = 60 and difference of two sides;
PR – PQ = 2 cm
Required: To construct PQR.
Steps of construction:
1. Draw a ray QX and cut off a line segment QR = 6 cm from it.
2. Construct a ray QY making an angle of 60 with QR and produce YQ to form a line YQY′.
3. Cut off a line segment QO = 2 cm
( PR – PQ = 2 cm) from QY′.
4. Join OR.
5. Draw perpendicular bisector MN of OR intersecting QY at a point P.
6. Join PR.
Then PQR is the required triangle.
P lies on perpendicular bisector of OR.
PO = PR
PQ + QO = PR
QO = PR – PQ
PR – PQ = 2 cm
(Which is true as given)
Question 13:
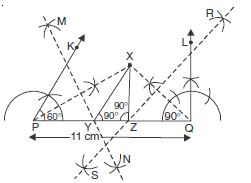
Construct a triangle XYZ in which ∠Y = 30, ∠Z = 90 and XY + YZ + ZX = 11 cm.
Answer:
Given: ∠Y = 30 and ∠Z = 90
Sum of three sides XY + YZ + ZX = 11 cm
Required: To construct XYZ.
Steps of construction:
1. Draw a line segment say PQ = 11 cm
( XY + YZ + ZX = 11 cm).
2. Draw ∠KPQ = 60 ( ∠Y = 60) and ∠LQP = 90 ( ∠Z = 90)
3. Bisect the ∠KPQ and ∠LQP. Let these intersect at point X.
4. Let MN intersect PQ at Y and RS intersect PQ at Z.
Join XY and XZ.
Then XYZ is the required triangle.
Justification for construction:
We observe that Y lies on perpendicular
bisector MN of PX.
PY = XY and
Similarly, QZ = XZ
This gives XY + YZ + ZX
= PY + YZ + QZ = PQ = 11 cm
(Which is true as given)
Again, ∠YXP = ∠XPY
(As in XPY; XY = PY)
∠XYZ = ∠YXP + ∠XPY
= 2∠XPY = ∠KPQ
∠XYZ = 30
(Which is true as given)
Similarly,∠XZY = ∠LQP
∠XZY = 90
(Which is true as given)
Question 14:
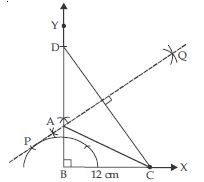
Construct a right triangle whose base is 12 cm and sum of its hypotenuse and other side is 18 cm.
Answer:
Let ABC is to be constructed with base BC = 12 cm, the sum of its other side and
hypotenuse.
i.e., AB + AC = 18 cm
and ∠ABC = 90
Steps of construction:
1. Draw a ray BX and cut off a line segment BC = 12 cm from it.
2. Construct ∠XBY = 90.
3. From BY cut off a line segment BD = 18 cm.
4. Join CD.
5. Draw the perpendicular bisector of CD intersecting BD at A.
6. Join AC.
Then, ABC is the required right triangle.
A lies on the perpendicular bisector of CD.
AC = AD and then
AB = BD – AD
AB = BD – AC
AB + AC = BD = 18 cm.
i.e., Sum of other side and hypotenuse is 18 cm. (which is true as per given statement)