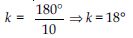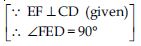Question 1:
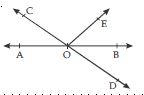
In fig., lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70 and ∠BOD = 40, find ∠BOE and reflex ∠COE.
Answer:
∠AOC + ∠COE + ∠BOE = 180
(linear pair)
or (∠AOC + ∠BOE) + ∠COE = 180
70 + ∠COE = 180
∠COE = 180 – 70
∠COE = 110 ... (i)
Also,∠COE + ∠BOE + ∠BOD = 180
(linear pair)
110 + ∠BOE + 40 = 180
∠BOE = 180 – 110 – 40
∠BOE = 30
ALITER
∠AOC = ∠BOD
(Vertically opp. angles)
∠AOC = 40
[Since ∠BOD = 40 (given)]
Now ∠AOC + ∠BOE = 70 (given)
40 + ∠BOE = 70
∠BOE = 70 – 40
∠BOE = 30 Ans.
Reflex ∠COE
= 360 – ∠COE
= 360 – 110
= 250
Hence, reflex ∠COE = 250
Question 2:
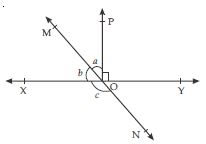
In fig., lines XY and MN intersect at O. If ∠POY = 90 and a : b = 2 : 3, find c.
Answer:
∠POX + ∠POY = 180 (linear pair)
∠POX + 90 = 180
∠POX = 180 – 90
∠POX = 90
Now let a = 2k and b = 3k
where k is a constant and k > 0
∠POX = 90
a + b = 90
2k + 3k = 90
5k = 90
Now, ∠MOX + ∠NOX = 180
(linear pair)
b + c = 180
54 + c = 180
c = 180 – 54
c = 126
Hence, measure of required c is 126
Question 3:
In fig., ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.
Answer:
According to given fig.,
∠PQS + ∠PQR = 180 ... (i)
(linear pair)
also ∠PRT + ∠PRQ = 180 ... (ii)
(linear pair)
From (i) and (ii), we get:
∠PQS + ∠PQR = ∠PRT + ∠PRQ ... (iii)
But ∠PQR = ∠PRQ (Given)
Therefore we can rewrite (iii) as
∠PQS + ∠PQR = ∠PRT + ∠PQR
∠PQS = ∠PRT + ∠PQR – ∠PQR
∠PQS = ∠PRT
Question 4:
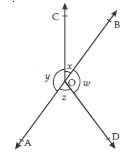
In fig., if x + y = w + z, then prove that AOB is a line.
Answer:
According to given figure,
∠AOC + ∠BOC + ∠DOB + ∠AOD = 360
x + y + w + z = 360
x + y + x + y = 360
[_ x + y = w + z (given)]
2x + 2y = 360
2(x + y) = 360
x + y = 180 (linear pair)
or ∠BOC + ∠AOC = 180
It shows that OC is the common arm of angles;
∠AOC and ∠BOC forming a linear pair.
Hence AOB is a line.
Question 5:
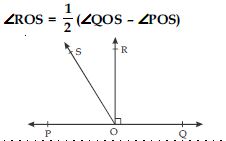
In fig., POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that:
Answer:
According to the given figure,
∠QOR + ∠POR = 180 (linear pair)
90 + ∠POR = 180
∠POR = 180 – 90
∠POR = 90
or ∠ROS + ∠POS = 90
∠ROS = 90 – ∠POS ...(i)
Again ∠QOS + ∠POS = 180 (linear pair) ...(ii)
Subtracting 2∠POS from the both sides of (ii),
we get:
∠QOS + ∠POS – 2∠POS = 180– 2∠POS
∠QOS – ∠POS = 2 (90 – ∠POS)
or
1/2 (∠QOS – ∠POS) = 90 – ∠POS ...(iii)
From (i) and (iii), we get
∠ROS =
1/2 (∠QOS – ∠POS)
Question 6:
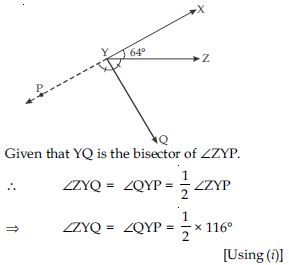
It is given that ∠XYZ = 64 and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP, find ∠XYQ and reflex ∠QYP.
Answer:
XY is produced to point P.
XP is a straight line.
Thus ∠XYZ + ∠ZYP = 180 (linear pair)
64 + ∠ZYP = 180
∠ZYP = 180 – 64
∠ZYP = 116 ... (i)
∠QYP = 58
Now ∠XYQ = ∠XYZ + ∠ZYQ
∠XYQ = 64 + 58
_ ∠XYZ = 64 (given)
and ∠ZYQ = 58
∠XYQ = 122
From (ii), we have ∠QYP = 58
reflex ∠QYP = 360 – ∠QYP
reflex ∠QYP = 360 – 58
reflex ∠QYP = 302
Question 7:
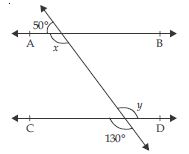
In fig., find the values of x and y and then show that AB || CD.
Answer:
Let transversal l intersects AB and CD at P and Q respectively.
According to given fig.,
50 + x = 180 (linear pair)
x = 180 – 50
x = 130 ...(i)
y = 130 ...(ii)
(vertically opposite angles)
From (i) and (ii), we observe that :
x = y
It shows that alternate interior angles are equal.
As we know that if a transversal (say l) intersects
two lines in such a way that a pair of alternate
interior angles are equal, then the two lines are
parallel.
Therefore, AB || CD.
Question 8:
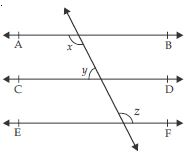
In fig., if AB || CD, CD || EF and y : z = 3 : 7, find x.
Answer:
AB || CD
x + y = 180 ...(i)
[_ Sum of the interior angles between two
parallel lines on the same side of a transversal
is 180]
Given that
AB || CD, CD || EF
AB || EF
[two lines which are parallel to the same
given line are parallel to each other.]
Therefore, x = z ...(ii)
[alternate interior angles for parallel lines are
equal]
Substituting the value of x from (ii) in (i), we get:
z + y = 180 ....(iii)
Given that y : z = 3 : 7
Let y = 3k z = 7k
where constant k > 0
Substituting the value of y and z in (iii), we get:
7k + 3k = 180
10k = 180
Therefore, y = 3k
y = 3 × 18
y = 54
and z = 7k
z = 7 × 18
z = 126
From (ii), we have x = z
x = 126.
Question 9:
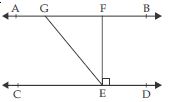
In fig., if AB || CD, EF CD and ∠GED = 126, find ∠AGE, ∠GEF and ∠FGE.
Answer:
AB || CD and GE is a transversal.
_ ∠AGE = ∠GED
[Alternate interior angles]
∠AGE = 126
[Since ∠GED = 126 (given)]
∠GED = 126 (given)
or ∠GEF + ∠FED = 126
∠GEF + 90 = 126
∠GEF = 126 –90
∠GEF = 36
Now ∠AGE + ∠FGE = 180 (linear pair)
126 + ∠FGE = 180
[_ ∠AGE = 126 (found above)]
∠FGE = 180 – 126
∠FGE = 54.
Question 10:
In fig., if AB || CD, EF CD and ∠GED = 126, find ∠AGE, ∠GEF and ∠FGE.
Answer:
AB || CD and GE is a transversal.
_ ∠AGE = ∠GED
[Alternate interior angles]
∠AGE = 126
[Since ∠GED = 126 (given)]
∠GED = 126 (given)
or ∠GEF + ∠FED = 126
∠GEF + 90 = 126
∠GEF = 126 –90
∠GEF = 36
Now ∠AGE + ∠FGE = 180 (linear pair)
126 + ∠FGE = 180
[_ ∠AGE = 126 (found above)]
∠FGE = 180 – 126
∠FGE = 54.
Question 11:
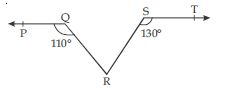
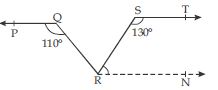
In fig., if PQ || ST, ∠PQR = 110 and ∠RST = 130, find ∠QRS.
[Hint: Draw a line parallel to ST through point R.]
Answer:
Through R ; draw a line RN parallel to ST.
Now, ST || RN
∠RST + ∠SRN = 180
[Since,Sum of the interior angles between two parallel lines on the same side of a
transversal line is 180.]
∠SRN = 180 – 130
∠SRN = 50 ...(i)
Now PQ || ST (given)
and RN || ST (By construction)
PQ || RN
[Since, two lines which are parallel to the same given line are parallel to each other]
Now PQ || RN and QR being a transversal.
∠QRN = ∠PQR
(alternate angles)
∠QRN = 110
[Since, PQR = 110 (given)]
∠QRS + ∠SRN = 110
∠QRS + 50 = 110 [Using (i)]
∠QRS = 110 – 50
∠QRS = 60.
Question 12:
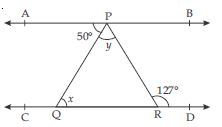
In fig., if AB || CD, ∠APQ = 50 and ∠PRD =127, find x and y.
Answer:
AB || CD ; PQ being a transversal.
x = ∠APQ
(alternate angles)
x = 50
[Since, ∠APQ = 50 (given)]
AB || CD ; PR being a transversal.
∠APR = ∠PRD
(alternate angles)
∠APQ + ∠QPR = ∠PRD
50 + y = 127
y = 127 – 50
y = 77.
Question 13:
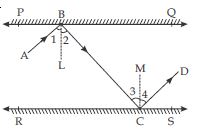
In fig., PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.
Answer:
According to the given figure; PQ and RS are two plane mirrors parallel to each other. AB is
an incident ray which strikes the mirror PQ at B. CD is the ray reflected from the mirror
RS.
We have to prove that
AB || CD
Proof : As we know that
angle of incidence = angle of reflection
∠1 = ∠2 and ∠3 = ∠4 ...(i)
∠1 is the angle between incident ray AB and
normal BL
∠1 is an incident angle,
∠2 is the angle between the reflected ray BC and normal BL. Therefore, ∠2 is a reflected
angle.
Similarly, ∠3 and ∠4 are the angles of incidence and reflection respectively.
∵ PQ || RS and BL PQ
and CM RS implies that
BL || CM
Now parallel lines BL and CM are cut by a
transversal BC.
∠2 = ∠3 (alternate angles) ...(ii)
Now, ∠ABC = ∠1 + ∠2
∠ABC = ∠2 + ∠2 [Since, ∠1 = ∠2]
∠ABC = 2∠2
and ∠BCD = ∠3 + ∠4
∠BCD = ∠3 + ∠3 [Since, ∠3 = ∠4]
∠BCD = 2∠3
But from (ii), we have
∠2 = ∠3
2∠2 = 2∠3
∠ABC = ∠BCD
These are alternate angles, BC being a
transversal.
Therefore, AB || CD. [Hence proved]
Question 14:
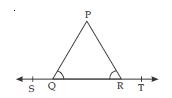
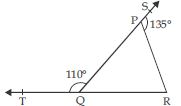
In the given fig., sides QP and RQ of PQR are produced to points S and T respectively. If ∠SPR = 135 and ∠PQT = 110, find ∠PRQ.
Answer:
∠SPR + ∠QPR = 180 (linear pair)
135+ ∠QPR = 180
∠QPR = 180 – 135
∠QPR = 45
As we know that an exterior angle of a triangle is equal to sum of its interior opposite
angles.
In PQR,
ext. ∠PQT = ∠QPR + ∠PRQ
110 = 45 + ∠PRQ
110 – 45 = ∠PRQ
65 = ∠PRQ
or ∠PRQ = 65
Question 15:
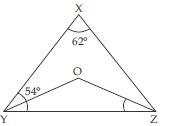
In the given fig., ∠X = 62, ∠XYZ = 54. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of XYZ, find ∠OZY and ∠YOZ.
Answer:
In XYZ,
∠X + ∠XYZ + ∠XZY = 180
(angle sum property of a triangle)
62 + 54 + ∠XZY = 180
∠XZY = 180 – 62 – 54
∠XZY = 64
Now ZO is the bisector of ∠XZY.
∠OYZ = 27
Now in OYZ;
∠YOZ + ∠OYZ + ∠OZY = 180
(angle sum property of a triangle)
∠YOZ + 27 + 32 = 180
∠YOZ = 180 – 27 – 32
∠YOZ = 121
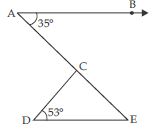
Question 16:
In the given fig., if AB || DE, ∠BAC = 35 and ∠CDE = 53, find ∠DCE.
Answer:
AB || DE and AE being a transversal.
∠BAE = ∠AED
(alternate angles)
or ∠BAC = ∠AED
35 = ∠AED
or ∠AED = 35
or ∠CED = 35
Now in CDE;
∠DCE + ∠CDE + ∠CED = 180
(angle sum property of a triangle)
∠DCE + 53 + 35 = 180
∠DCE + 88 = 180
∠DCE = 180 – 88
∠DCE = 92
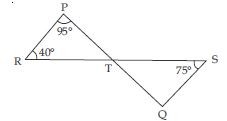
Question 17:
In the given fig., if lines PQ and RS intersect at point T, such that ∠PRT = 40, ∠RPT = 95 and ∠TSQ = 75, find ∠SQT.
Answer:
In PRT;
∠RPT + ∠PRT + ∠PTR = 180
(angle sum property of a triangle)
95 + 40 + ∠PTR = 180
∠PTR = 180 – 95 – 40
∠PTR = 180 – 135
∠PTR = 45 ... (i)
PQ and RS intersect at point T.
∠STQ = ∠PTR
(Vertically opp. angles)
∠STQ = 45 [Using (i)]
Now in STQ;
∠SQT + ∠STQ + ∠QST= 180
(angle sum property of a triangle)
∠SQT + 45 + 75 = 180
∠SQT = 180 – 45 – 75
∠SQT = 180 – 120
∠SQT = 60
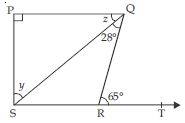
Question 18:
In the given fig., if PQ PS, PQ || SR, ∠SQR = 28 and ∠QRT = 65, then find the values of x and y.
Answer:
As we know that exterior angle of a triangle is equal to sum of its interior opposite
angles.
In QSR,
ext. ∠QRT = ∠QSR + ∠SQR
65 = ∠QSR + 28
65 – 28 = ∠QSR
or ∠QSR = 37 ... (i)
PQ || SR and SQ being a transversal
x = ∠QSR
x = 37 [Using (i)] ...(ii)
PQ PS
∠QPS = 90 ...(iii)
In rt ∠d PQS;
∠QPS + x + y = 180
(angles sum property)
90 + 37 + y = 180 [Using (ii) and (iii)]
127 + y = 180
y = 180 – 127
y = 53
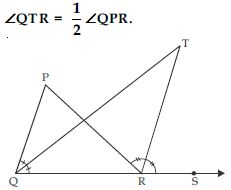
Question 19:
In the given fig., the side QR of PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that
Answer:
QT is bisector of ∠PQR
∠PQT = ∠RQT ... (i)
RT is the bisector of ∠PRS.
∠PRT = ∠TRS ... (ii)
As we know that exterior angle of a triangle is equal to sum of its interior opposite
angles.
In PQR
ext. ∠PRS = ∠QPR + ∠PQR
(∠PRT + ∠TRS) = ∠QPR + (∠PQT + ∠RQT)
∠TRS + ∠TRS =∠QPR + (∠RQT + ∠RQT)
[Using (i) and (ii)]
2∠TRS =∠QPR + 2∠RQT
2(∠TRS – ∠RQT) = ∠QPR