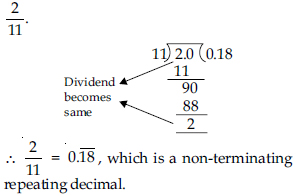
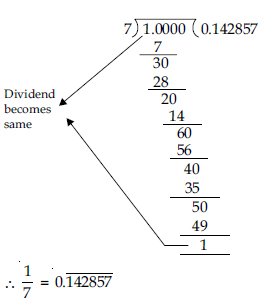
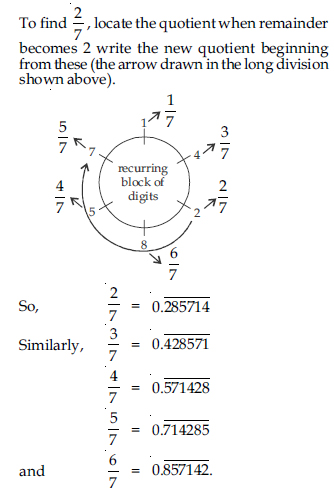
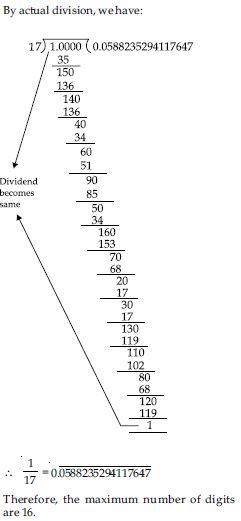
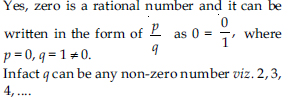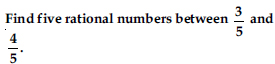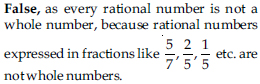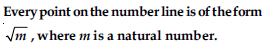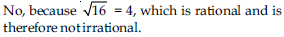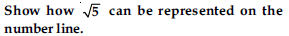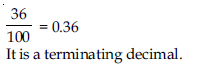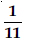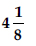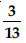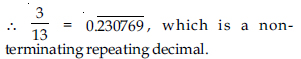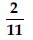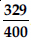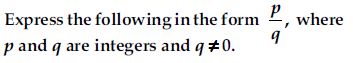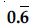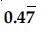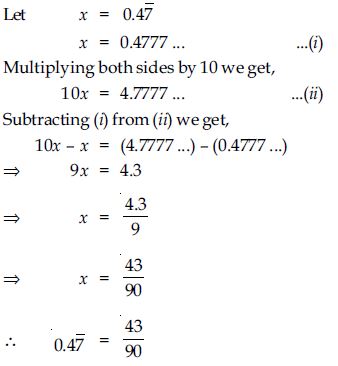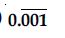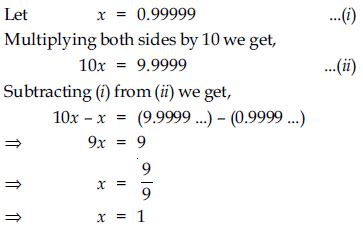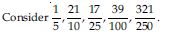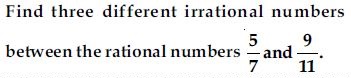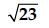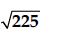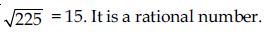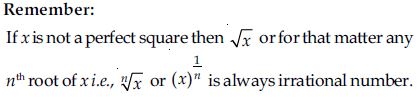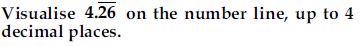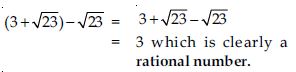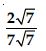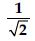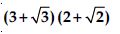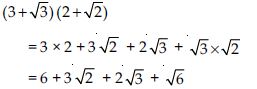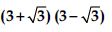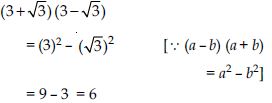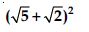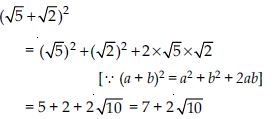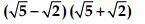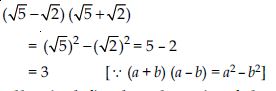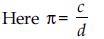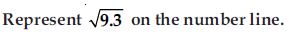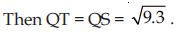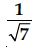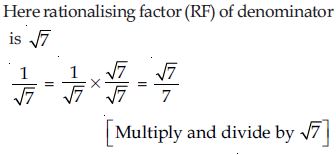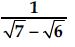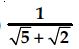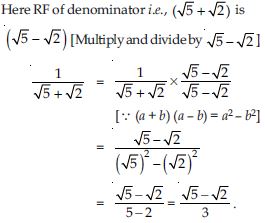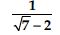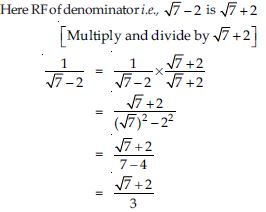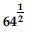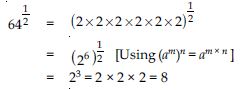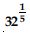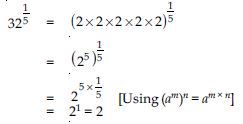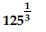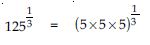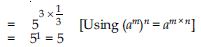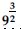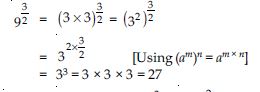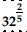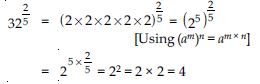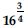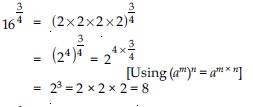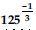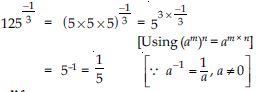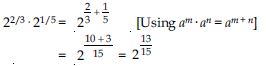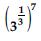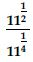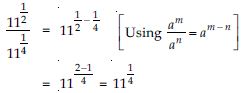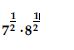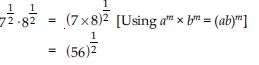NCERT Solutions for Class 9 Math Number System

Question 1:

Is zero a rational number? Can you write it in the form p/q, where p and q are integers and q $\neq$ 0?

Answer:

Show Answer

Question 2:

Find six rational numbers between 3 and 4.

Answer:

Show Answer

Question 3:

Answer:

Show Answer

Question 4:

Every natural number is a whole number.
TRUE
FALSE

Answer:

True, since, collection of whole numbers contains all natural numbers.

Show Answer

Question 5:

Every integer is a whole number.
TRUE
FALSE

Answer:

False, as every integer is not a whole number, because negative integers are not whole numbers.

Show Answer

Question 6:

Every rational number is a whole number.
TRUE
FALSE

Answer:

Show Answer

Question 7:

Every irrational number is a real number.
TRUE
FALSE

Answer:

True.
Justification: Because set of rational and irrational numbers constitute the set of real numbers. In other words all irrational numbers are real numbers. Hence, the statement ‘every irrational number is a real number’ is true.

Show Answer

Question 8:

Answer:

False.
Justification: – 3, – 5, – 9 are all real numbers but none of these is square root of any natural number.

Show Answer

Question 9:

Every real number is an irrational number.
TRUE
FALSE

Answer:

False.
Justification: 5, 7, 8, 11 are all real numbers but none is irrational.

Show Answer

Question 10:

Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.

Answer:

Show Answer

Question 11:

Answer:

Show Answer

Question 12:

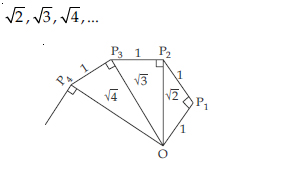
Classroom activity (Constructing the ‘square root spiral’):

Answer:

Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment OP₁ of unit length. Draw a line segment P₁P₂ perpendicular to OP₁ of unit length [see figure]. Now draw a line segment P₂P₃ perpendicular to OP₂. Then draw a line segment P₃P₄ perpendicular to OP₃. Continuing in this manner, you can get the line segment P_n–1P_n by drawing a line segment of unit length perpendicular to OP _n–1 . In this manner, you will have created the points P₂, P₃, ..., P_n, ... and joined them to create a beautiful spiral depicting

Show Answer

Question 13:

Write the following in decimal form and say what kind of decimal expansion each has:

Answer:

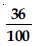
Show Answer

Question 14:

Write the following in decimal form and say what kind of decimal expansion each has:

Answer:

Show Answer

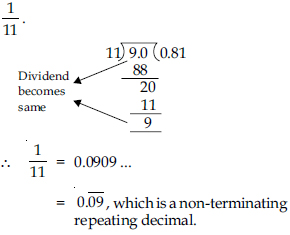
Question 15:

Write the following in decimal form and say what kind of decimal expansion each has:

Answer:

Show Answer

Question 16:

Write the following in decimal form and say what kind of decimal expansion each has:

Answer:

Show Answer

Question 17:

Write the following in decimal form and say what kind of decimal expansion each has:

Answer:

Show Answer

Question 18:

Write the following in decimal form and say what kind of decimal expansion each has:

Answer:

Show Answer

Question 19:

Answer:

Show Answer

Question 20:

Answer:

Note: (i) First shift all non-repeating digits (say m digits in total) LHS by multiplying both sides with 10^m.
(ii) Then shift block of recurring digits (say a block of n recurring digits to LHS by multiplying both sides with 10ⁿ.

Show Answer

Question 21:

Answer:

Show Answer

Question 22:

Answer:

Show Answer

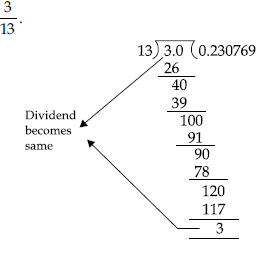
Question 23:

Answer:

Yes, at a glance we are surprised at our answer. But the answer makes sense when we observe that 0.9999... goes on forever. So there is no gap between 1 and 0.9999... and hence they are equal.

Show Answer

Question 24:

Answer:

Show Answer

Question 25:

Answer:

Observe that the denominator (q) of each of above number has prime 2 or 5 or both or their certain whole number power (index) as its factor.
So, we can say that denominator q of terminating decimal number has prime factors of the form 2^m × 5ⁿ where m and n are any whole numbers.

Show Answer

Question 26:

Write three numbers whose decimal expansions are non-terminating non-recurring.

Answer:

Three non-terminating, non-recurring numbers are:
0.201001000100001 ...
0.3516511651116511116...
0.4610792158921821689351...
Note: Answers to this question is not unique. Different answers are possible.

Show Answer

Question 27:

Answer:

Any three of these are:
0.75075007500075000075...,
0.767076700767000... and
0.80800800080000…

Show Answer

Question 28:

Classify the following numbers as rational or irrational:

Answer:

Show Answer

Question 29:

Classify the following numbers as rational or irrational:

Answer:

Show Answer

Question 30:

Classify the following numbers as rational or irrational:
0.3796

Answer:

0.3796. It is a terminating decimal, so it is a rational number.

Show Answer

Question 31:

Classify the following numbers as rational or irrational:
7.478478....

Answer:

Show Answer

Question 32:

Classify the following numbers as rational or irrational:
1.101001000100001...

Answer:

1.101001000100001...
It is a non-terminating non-recurring decimal, so it is an irrational number.

Show Answer

Question 33:

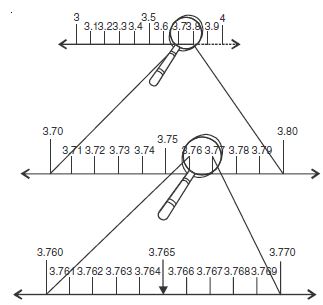
Visualise 3.765 on the number line, using successive magnification.

Answer:

Step (i) The given number lies between 3 and 4.

Step (ii) Magnify the interval between 3 and 4 divided is into 10 equal parts.
Step (iii) The given number lies between 3.7 and 3.8.
Step (iv) Divide the interval 3.7 and 3.8 into ten equal parts and magnify it.
Step (v) The given number lies between 3.76 and 3.77.
Step (vi) Magnify the interval between 3.76 and 3.77 and divide it into ten equal parts.
Step (vii) 3.765 is the fifth division in the magnification.

Show Answer

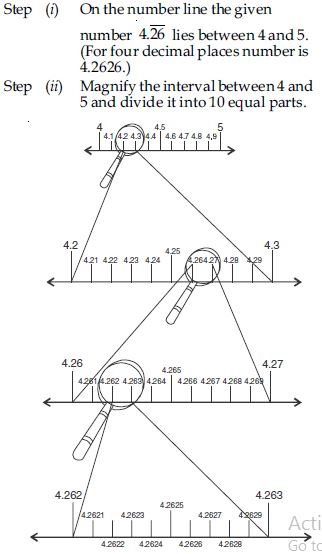
Question 34:

Answer:

Step (iii) The given number 4.2626 lies between 4.2 and 4.3.
Step (iv) Magnify the interval between 4.2 and 4.3 and divide it into ten equal parts.
Step (v) The given number falls between 4.26 and 4.27.
Step (vi) Magnify the interval between 4.26 and 4.27 and divide it into ten equal parts.
Step (vii) The given number lies between 4.262 and 4.263.
Step (viii) Magnify the interval between 4.262 and 4.263 and divide it into ten equal parts.

Show Answer

Question 35:

Classify the following numbers as rational or irrational :

Answer:

Show Answer

Question 36:

Classify the following numbers as rational or irrational :

Answer:

Show Answer

Question 37:

Classify the following numbers as rational or irrational :

Answer:

Show Answer

Question 38:

Classify the following numbers as rational or irrational :

Answer:

Show Answer

Question 39:

Classify the following numbers as rational or irrational :
2 $π$

Answer:

In given number; 2 is a non-zero rational number and $π$ is an irrational number. As we know that product of a non-zero rational number and an irrational number is always an irrational number.
So, 2 $π$ is an irrational number.

Show Answer

Question 40:

Simplify each of the following expressions:

Answer:

Show Answer

Question 41:

Simplify each of the following expressions:

Answer:

Show Answer

Question 42:

Simplify each of the following expressions:

Answer:

Show Answer

Question 43:

Simplify each of the following expressions:

Answer:

Show Answer

Question 44:

Answer:

As we know that quotient of a non-zero rational number and an irrational number or quotient of an irrational number with nonzero rational number is always an irrational number.

Therefore, there is no contradiction as either c or d are irrational hence, $π$ is an irrational number.
Eye Opener:
The value of $π$ up to 20 decimal places is 3.14159 26535 89893 23846... The value of $π$ has been calculated up to 100265 digits, but no sign of recurrence of digits was found. It is thus not a recurring decimal number. So $π$ is an irrational number.

Show Answer

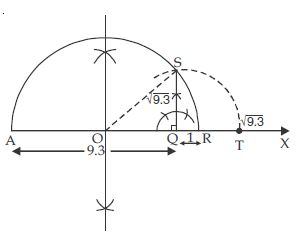
Question 45:

Answer:

(i) Draw a ray AX.
(ii) Mark a point Q on the ray such that AQ = 9.3 units.
(iii) From Q, mark a point R such that QR = 1 unit.
(iv) Draw perpendicular bisector of AR to obtain mid-point. Let us mark it as O.
(v) Taking O as centre and OR as radius draw a semicircle.
(vi) Draw QS ⊥ AX which cuts semicircle at S.
(vii) Taking Q as centre and QS as radius draw an arc cutting AX at T.