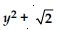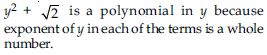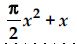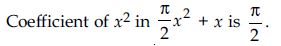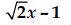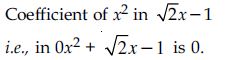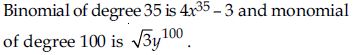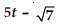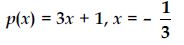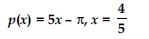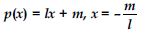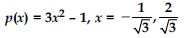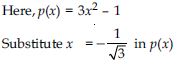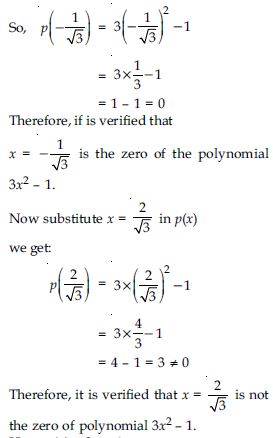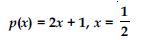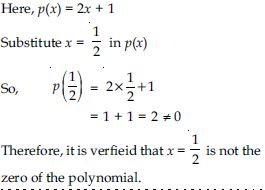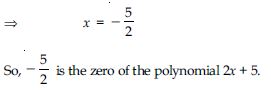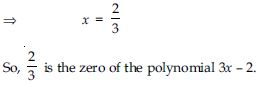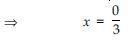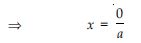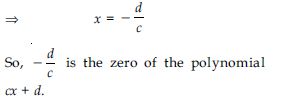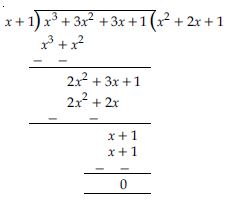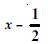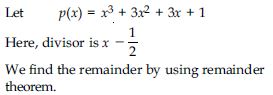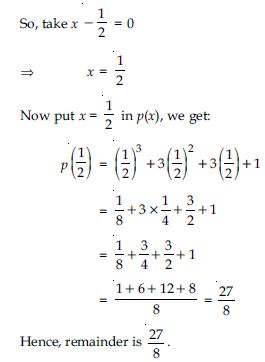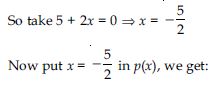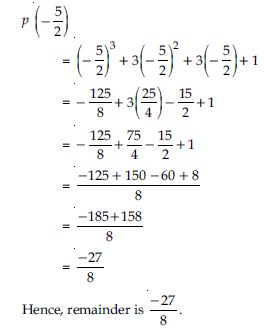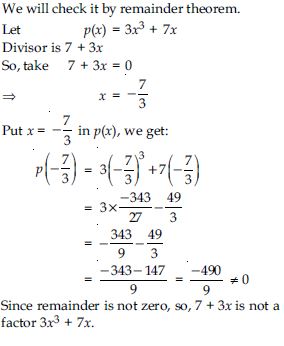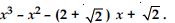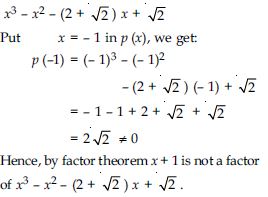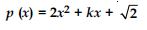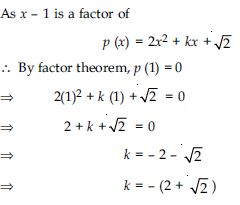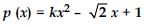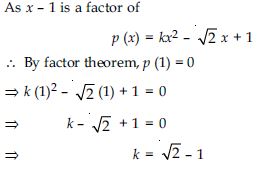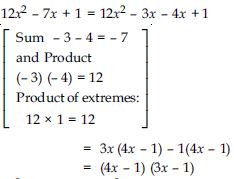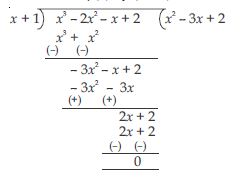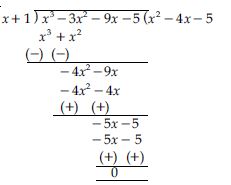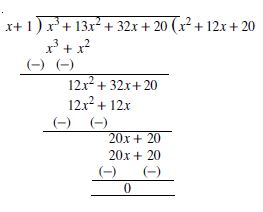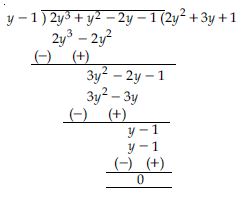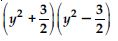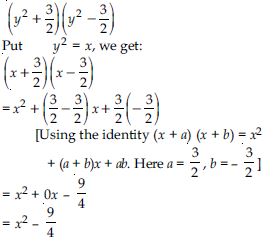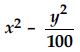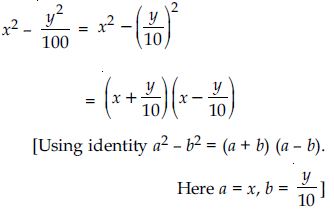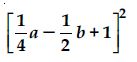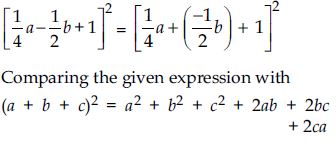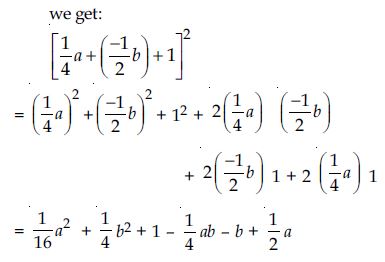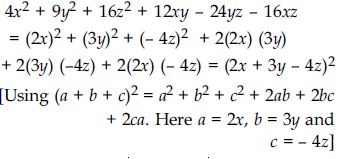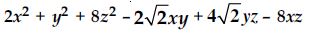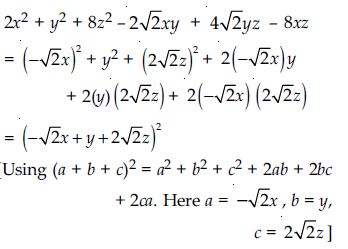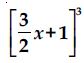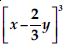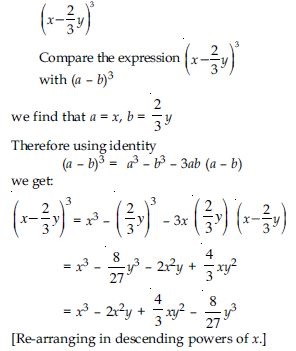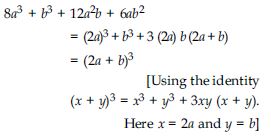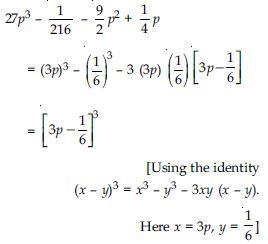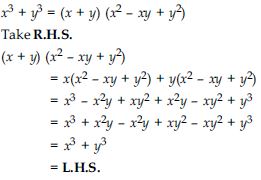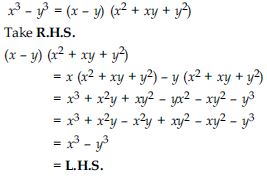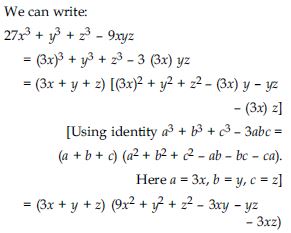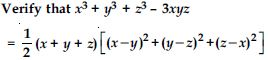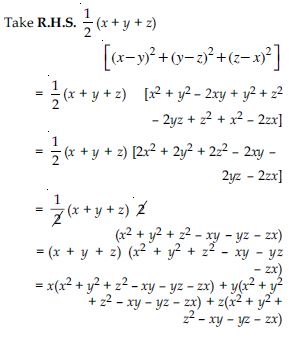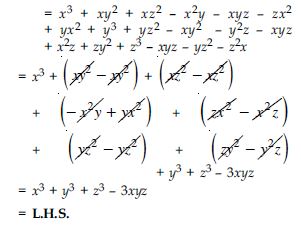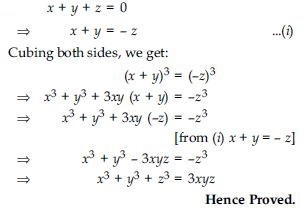Question 1:
Which of the following expressions are polynomials in one variable and which are not? State
reasons for your answer.
4x2 – 3x + 7
Answer:
4x2 – 3x + 7 is a polynomial in x because exponent of x in each of the terms is a whole number.
Question 2:
Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer.
Answer:
Question 3:
Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer.
Answer:
Question 4:
Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer.
Answer:
Question 5:
Which of the following expressions are polynomials in one variable and which are not? State
reasons for your answer.
x10 + y3 + t50
Answer:
x10 + y3 + t50 is a polynomial in three variables x, y and t, because exponent of each variable is a whole number.
Question 6:
Write the coefficients of x2 in each of the following:
2 + x2 + x
Answer:
Coefficient of x2 in 2 + x2 + x is 1.
Question 7:
Write the coefficients of x2 in each of the following:
2 – x2 + x3
Answer:
Coefficient of x2 in 2 – x2 + x3 is –1.
Question 8:
Write the coefficients of x2 in each of the following:
Answer:
Question 9:
Write the coefficients of x2 in each of the following:
Answer:
Question 10:
Give one example each of binomial of degree 35, and of a monomial of degree 100.
Answer:
Note: We can write some more polynomials with different coefficients.
Question 11:
Write the degree of each of the following polynomials:
5x3 + 4x2 + 7x
Answer:
Highest power term in p(x) is 5x3 and the exponent is 3. So, the degree is 3.
Question 12:
Write the degree of each of the following polynomials:
4 – y2
Answer:
Highest power term in p(y) is – y2 and the exponent is 2. So, the degree is 2.
Question 13:
Write the degree of each of the following polynomials:
Answer:
Highest power term in f(t) is 5t and the exponent is 1. So, the degree is 1.
Question 14:
Write the degree of each of the following polynomials:
3
Answer:
The only term here is 3 which can be written as 3x0 and so the exponent is 0. Therefore, the degree is 0.
Question 15:
Classify the following as linear, quadratic and cubic polynomials:
x2 + x
Answer:
The polynomial x2 + x is of degree 2. Therefore, it is a quadratic polynomial.
Question 16:
Classify the following as linear, quadratic and cubic polynomials:
x – x3
Answer:
The polynomial x – x3 is of degree 3. Therefore, it is a cubic polynomial.
Question 17:
Classify the following as linear, quadratic and cubic polynomials:
y + y2 + 4
Answer:
The polynomial y + y2 + 4 is of degree 2. Therefore, it is a quadratic polynomial.
Question 18:
Classify the following as linear, quadratic and cubic polynomials:
1 + x
Answer:
Polynomial 1 + x is of degree 1. Therefore, it is a linear polynomial.
Question 19:
Classify the following as linear, quadratic and cubic polynomials:
3t
Answer:
3t is a polynomial of degree 1. Therefore, it is a linear polynomial.
Question 20:
Classify the following as linear, quadratic and cubic polynomials:
r2
Answer:
r2 is a polynomial of degree 2. Therefore, it is a quadratic polynomial.
Question 21:
Write the degree of each of the following polynomials:
7x3
Answer:
7x3 is a polynomial of degree 3. Therefore, it is a cubic polynomial.
Question 22:
Find the value of the polynomial 5x – 4x2 + 3 at
x = 0
Answer:
The value of polynomial
p(x) = 5x – 4x2 + 3 at x = 0 is given by
= 5(0) – 4(0)2 + 3 = 0 – 0 + 3 = 3
Question 23:
Find the value of the polynomial 5x – 4x2 + 3 at
x = –1
Answer:
The value of polynomial
p(x) = 5x – 4x2 + 3 at x = –1 is given by
= 5 (–1) – 4 (–1)2 + 3
= – 5 – 4 + 3 = –6
Question 24:
Find the value of the polynomial 5x – 4x2 + 3 at
x = 2
Answer:
The value of polynomial
p(x) = 5x – 4x2 + 3 at x = 2 is given by
= 5(2) – 4(2)2 + 3 = 10 – 4 × 4 + 3 = 10 – 16 + 3 = –3
Question 25:
Find p(0), p(1) and p(2) for each of the following polynomials:
p(y) = y2 – y + 1
Answer:
p(y) = y2 – y + 1
p(0) = (0)2 – 0 + 1
p(0) = 1
p(1) = (1)2 – 1 + 1
p(1) = 1 – 1 + 1
p(1) = 1
p(2) = (2)2– 2 + 1
p(2) = 4 – 2 + 1
p(2) = 3
Question 26:
Find p(0), p(1) and p(2) for each of the following polynomials:
p(t) = 2 + t + 2t2 – t3
Answer:
p(t) = 2 + t + 2t2 – t3
p(0) = 2 + 0 + 2(0)2 – (0)3
p(0) = 2 + 0 + 0 – 0
p(0) = 2
p(1) = 2 + 1 + 2(1)2 – (1)3
p(1) = 2 + 1 + 2 – 1
p(1) = 4
p(2) = 2 + 2 + 2(2)2 – (2)3
p(2) = 2 + 2 + 8 – 8
p(2) = 4
Question 27:
Find p(0), p(1) and p(2) for each of the following polynomials:
p(x) = x3
Answer:
p(x) = x3
p(0) = (0)3
p(0) = 0
p(1) = (1)3
p(1) = 1
p(2) = (2)3
p(2) = 8
Question 28:
Find p(0), p(1) and p(2) for each of the following polynomials:
p(x) = (x – 1) (x + 1).
Answer:
p(x) = (x – 1) (x + 1)
p(0) = (0 – 1) (0 + 1)
p(0) = (– 1) × (1)
p(0) = –1
p(1) = (1 – 1) (1 + 1)
p(1) = 0 × 2
p(1) = 0
p(2) = (2 – 1) (2 + 1)
p(2) = 1 × 3
p(2) = 3
Question 29:
Verify whether the following are zeros of the polynomial, indicated against them.
Answer:
Question 30:
Verify whether the following are zeros of the polynomial, indicated against them.
Answer:
Question 31:
Verify whether the following are zeros of the polynomial, indicated against them.
p(x) = x2 – 1, x = 1, – 1
Answer:
Here, p(x) = x2 – 1
Substitute x = 1 in p(x)
So, p(1) = (1)2 – 1
= 1 – 1
p(1) = 0
Therefore, x = 1 is the zero of the polynomial
x2 – 1. Now substitute x = – 1, in the given
polynomial.
So, p( – 1) = ( – 1)2 – 1
= 1 – 1
p( – 1) = 0
Therefore, x = – 1 is the zero of the
polynomial x2 – 1.
Question 32:
Verify whether the following are zeros of the polynomial, indicated against them.
p(x) = (x + 1) (x – 2), x = – 1, 2
Answer:
Here, p(x) = (x + 1) (x – 2)
Substitute x = – 1 in p(x)
So, p( – 1) = ( – 1 + 1) (– 1 – 2)
= 0 ( – 3)
= 0
Therefore, it is verified that x = – 1
is the zero of the polynomial
(x + 1) (x – 2)
Now substitute x = 2 in p(x)
So, p(2) = (2 + 1) (2 – 2)
= 3 × 0
p(2) = 0
Therefore, it is verified that x = 2 is the zero
of the polynomial (x + 1) (x – 2)
Question 33:
Verify whether the following are zeros of the polynomial, indicated against them.
p(x) = x2, x = 0
Answer:
Here, p(x) = x2
Substitute x = 0 in p(x)
So, p(0) = (0)2
p(0) = 0
Therefore, it is verified that x = 0 is the zero
of the polynomial x2.
Question 34:
Verify whether the following are zeros of the polynomial, indicated against them.
Answer:
Question 35:
Verify whether the following are zeros of the polynomial, indicated against them.
Answer:
Question 36:
Verify whether the following are zeros of the polynomial, indicated against them.
Answer:
Question 37:
Find the zero of the polynomial in each of the following cases:
p(x) = x + 5
Answer:
As finding the zero of the polynomial p(x) amounts to solve the equation p(x) = 0,
We have, x + 5 = 0
x = – 5
So, – 5 is the zero of the polynomial x + 5
Question 38:
Find the zero of the polynomial in each of the following cases:
p(x) = x – 5
Answer:
As finding the zero of the polynomial p(x) amounts to solve the equation p(x) = 0
We have, x – 5 = 0
x = 5
So, 5 is the zero of the polynomial x – 5
Question 39:
Find the zero of the polynomial in each of the following cases:
p(x) = 2x + 5
Answer:
As finding the zero of the polynomial p(x) amounts to solve the equation p(x) = 0.
We have,
2x + 5 = 0
2x = – 5
Question 40:
Find the zero of the polynomial in each of the following cases:
p(x) = 3x – 2
Answer:
As finding the zero of the polynomial p(x) amounts to solve the equation p(x) = 0.
We have,
3x – 2 = 0
3x = 2
Question 41:
Find the zero of the polynomial in each of the following cases:
p(x) = 3x
Answer:
As finding the zero of the polynomial p(x) amounts to solve the equation p(x) = 0.
We have, 3x = 0
x = 0
So, 0 is the zero (root) of the polynomial 3x.
Question 42:
Find the zero of the polynomial in each of the following cases:
p(x) = ax, a 0
Answer:
As finding the zero of the polynomial p(x) amounts to solve the equation p(x) = 0.
We have, ax = 0
So, 0 is the zero (root) of the polynomial ax.
Question 43:
Find the zero of the polynomial in each of the following cases:
p(x) = cx + d, c 0, c, d are real numbers.
Answer:
As finding the zero of the polynomial p(x) amounts to solve the equation p(x) = 0
We have, cx + d = 0
where c 0, c, d are real numbers
cx = – d
x = 0
So, 0 is the zero (root) of the polynomial ax.
Question 44:
Find the remainder when x3 + 3x2 + 3x + 1 is divided by:
x + 1
Answer:
Let p(x) be x3 + 3x2 + 3x + 1 and divisor is x + 1.
Remainder by long division method is as follows:
ALITER. Finding of remainder by using
remainder theorem.
Let p (x) = x3 + 3x2 + 3x + 1
Divisor is x + 1
So, take x + 1 = 0
x = – 1
Put x = – 1 in p(x), we get:
p( – 1) = (–1)3 + 3 (–1)2 + 3( – 1) + 1
= – 1 + 3 – 3 + 1
p ( – 1) = 0
Hence, remainder is 0.
Question 45:
Find the remainder when x3 + 3x2 + 3x + 1 is divided by:
x
Answer:
Question 46:
Find the remainder when x3 + 3x2 + 3x + 1 is divided by:
x +
Answer:
Let p(x)= x3 + 3x2 + 3x + 1
Here, divisor is x + .
We find the remainder by using remainder
theorem.
So, take x + = 0
x = –
Now put x = – in p(x), we get:
p() = (– )3 + 3(– )2 + 3(–) + 1
= – 3 + 32 – 3 + 1
Question 47:
Find the remainder when x3 + 3x2 + 3x + 1 is divided by:
5 + 2x
Answer:
Let p(x) = x3 + 3x2 + 3x + 1
Here, divisor is 5 + 2x
We find the remainder by using the remainder theorem
Question 48:
Find the remainder when
x3 – ax2 + 6x – a is divided by x – a.
Answer:
Let p(x) = x3 – ax2 + 6x – a
Divisor is x – a
So, take x – a = 0
x = a
put x = a in p(x), we get:
p(a) = a3 – a(a)2 + 6a – a
= a3 – a3 + 6a – a
= 5a
p(a) = 5a
Hence, remaninder is 5a.
Question 49:
Check whether 7 + 3x is a factor of 3x3 + 7x.
Answer:
Question 50:
Determine which of the following polynomials has (x + 1) a factor:
x3 + x2 + x + 1
Answer:
Let p (x) = x3 + x2 + x + 1
Put x = – 1 in p (x), we get:
p (–1) = (–1)3 + (–1)2 + (–1) + 1
= – 1 + 1 – 1 + 1
= 0
Hence, by factor theorem x + 1 is a factor of
x3 + x2 + x + 1.
Question 51:
Determine which of the following polynomials has (x + 1) a factor:
x4 + x3 + x2 + x + 1
Answer:
Let p (x) = x4 + x3 + x2 + x + 1
Put x = –1 in p (x), we get:
p (–1) = (–1)4 + (–1)3 + (–1)2 + (–1) + 1
= 1 – 1 + 1 – 1 + 1
= 1 ≠ 0
Hence, by factor theorem x + 1 is not a factor
of x4 + x3 + x2 + x + 1.
Question 52:
Determine which of the following polynomials has (x + 1) a factor:
x4 + 3x3 + 3x2 + x + 1
Answer:
Let p (x) = x4 + 3x3 + 3x2 + x + 1
Put x = –1 in p (x), we get:
p (–1) = (–1)4 + 3(–1)3 + 3(–1)2 + (–1) + 1
= 1 – 3 + 3 – 1 + 1
= 1 ≠ 0
Hence, by factor theorem x + 1 is not a factor
of x4 + 3x3 + 3x2 + x + 1.
Question 53:
Determine which of the following polynomials has (x + 1) a factor:
Answer:
Question 54:
Use the Factor Theorem to determine whether g(x) is a factor of p(x) in ach of the following
cases:
p(x) = 2x3 + x2 – 2x – 1, g(x) = x + 1
Answer:
We have,
p (x) = 2x3 + x2 – 2x – 1
and divisor; g (x) = x + 1
Take (x + 1) = 0 x = –1
Put x = –1 in p (x), we get:
p (–1) = 2 (–1)3 + (–1)2 – 2(–1) – 1
= – 2 + 1 + 2 – 1 = 0
Hence, by factor theorem x + 1 i.e. g (x) is
a factor of 2x3 + x2 – 2x – 1.
Question 55:
Use the Factor Theorem to determine whether g(x) is a factor of p(x) in ach of the following
cases:
p(x) = x3 + 3x2 + 3x + 1, g(x) = x + 2
Answer:
We have,
p (x) = x3 + 3x2 + 3x + 1
and divisor; g (x) = x + 2
Take x + 2 = 0
x = –2
Put x = – 2 in p (x), we get:
p (–2) = (–2)3 + 3(–2)2 + 3(–2) + 1
= – 8 + 12 – 6 + 1
= – 1 ≠ 0
Hence, by factor theorem x + 2 i.e. g (x) not
a factor of x3 + 3x2 + 3x + 1.
Question 56:
Use the Factor Theorem to determine whether g(x) is a factor of p(x) in ach of the following
cases:
p(x) = x3 – 4x2 + x + 6, g(x) = x – 3
Answer:
We have,
p (x) = x3 – 4x2 + x + 6
and divisor; g(x) = x – 3
Take x – 3 = 0
x = 3
Put x = 3 in p (x), we get:
p (3) = (3)3 – 4 (3)2 + 3 + 6
= 27 – 36 + 3 + 6
= 36 – 36
= 0
Hence, by factor theorem x – 3, i.e. g (x) is a
factor of x3 – 4x2 + x + 6.
Question 57:
Find the value of k, if x – 1 is a factor of p(x) in each of the following cases:
p (x) = x2 + x + k
Answer:
As x – 1 is a factor of
p (x) = x2 + x + k
By factor theorem, p (1) = 0
(1)2 + 1 + k = 0
1 + 1 + k = 0
2 + k = 0
k = –2
Question 58:
Find the value of k, if x – 1 is a factor of p(x) in each of the following cases:
Answer:
Question 59:
Find the value of k, if x – 1 is a factor of p(x) in each of the following cases:
Answer:
Question 60:
Find the value of k, if x – 1 is a factor of p(x) in each of the following cases:
p (x) = kx2 – 3x + k.
Answer:
As x – 1 is a factor of
p (x) = kx2 – 3x + k
By factor theorem,
p (1) = 0
k (1)2 – 3(1) + k = 0
k – 3 + k = 0
2k = 3
Question 61:
Factorise:
12x2 – 7x + 1
Answer:
Question 62:
Factorise:
2x2 + 7x + 3
Answer:
2x2 + 7x + 3 = 2x2 + 6x + x + 3
= 2x(x + 3) + 1(x + 3)
= (x + 3)(2x + 1)
Question 63:
Factorise:
6x2 + 5x – 6
Answer:
6x2 + 5x – 6 = 6x2 + 9x – 4x – 6
= 3x (2x + 3) – 2 (2x + 3)
= (2x + 3) (3x – 2)
Question 64:
Factorise:
3x2 – x – 4
Answer:
3x2 – x – 4 = 3x2 – 4x + 3x – 4
= x(3x – 4) + 1(3x – 4)
= (3x – 4) (x + 1)
Question 65:
Factorise:
x3 – 2x2 – x + 2
Answer:
Let us denote the given polynomial as p(x)
So, p(x) = x3 – 2x2 – x + 2
All factors of +2 are 1, 2
By inspection,
p(–1) = (–1)3 –2(–1)2 – (–1) + 2
= – 1 – 2 + 1 + 2
p(–1) = 0
So, by factor theorem (x + 1) is a factor of p(x)
Now divide p(x) by (x + 1)
Thus x3 – 2x2– x + 2
= (x + 1) (x2 – 3x + 2)
The factors of x2 – 3x + 2 can be solved by
splitting the middle term or using factor
theorem.
By splitting the middle term,
we have
x2 – 3x + 2 = x2 – x – 2x + 2
= x(x – 1) –2(x – 1)
= (x – 1) (x – 2)
So, x3 – 2x2 – x + 2 = (x + 1) (x – 1) (x –2)
Question 66:
Factorise:
x3 – 3x2 – 9x – 5
Answer:
Let us denote the given polynomial as
p(x) = x3 – 3x2 – 9x – 5
All factors of –5 are 1, 5
By inspection,
p(–1) = (–1)3 –3 (–1)2 –9 (–1) – 5
= –1 – 3 + 9 – 5
= 9 – 9
= 0
So, by factor theorem x + 1 is a factor of p(x)
Now divide p(x) by x + 1.
Thus x3 – 3x2 – 9x – 5
= (x + 1) (x2 – 4x – 5)
Factors of x2 – 4x – 5 by splitting the middle
terms are as follows:
x2 – 4x – 5 = x2 – 5x + x – 5
= x(x – 5) + 1(x –5)
= (x – 5) (x + 1)
So, x3 – 3x2 – 9x – 5 = (x + 1) (x – 5) (x +1)
or = (x + 1) (x + 1) (x – 5)
Question 67:
Factorise:
x3 + 13x2 + 32x + 20
Answer:
Let us denote the given polynomial as
p(x) = x3 + 13x2 + 32x + 20
All factors of 20 are
1, 2, 4, 5, 10, 20
By inspection,
p(–1) = (–1)3 + 13(–1)2 + 32(–1) + 20
= – 1 + 13 – 32 + 20
= 33 – 33
p(–1) = 0
So, by factor theorem x + 1 is a factor of p(x).
Now divide p(x) by (x + 1)
Thus x3 + 13x2 + 32x + 20
= (x + 1) (x2 + 12x + 20)
Factors of x2 + 12x + 20 by splitting the
middle terms are as follows:
x2 + 12x + 20 = x2 + 2x + 10x + 20
= x(x + 2) + 10 (x + 2)
= (x + 2) (x + 10)
So, x3 + 13x2 + 32 x + 20
= (x + 1) (x + 2) (x + 10)
Question 68:
Factorise:
2y3 + y2 – 2y – 1
Answer:
Let us denote the given polynomial as
p(y) = 2y3 + y2 – 2y – 1
All factors of –1 are 1
By inspection,
p(1) = 2(1)3 + (1)2 – 2(1) – 1
= 2 + 1 – 2 – 1
= 3 – 3
p(1) = 0
So, by factor theorem; y – 1 is a factor of
p(y).
Now divide p(y) by y – 1.
Thus 2y3 + y2 – 2y – 1
= (y – 1) (2y2 + 3y + 1)
Factors of 2y2 + 3y + 1 by splitting the middle
terms are as follows:
2y2 + 3y + 1 = 2y2 + 2y + y + 1
= 2y (y + 1) + 1 (y + 1)
= (y + 1) (2y + 1)
So, 2y3 + y2 – 2y – 1
= (y – 1) (y + 1) (2y + 1)
Question 69:
Use the suitable identity to find the following products:
(x + 4) (x + 10)
Answer:
(x + 4) (x + 10)
= x2 + (4 + 10)x + 4 × 10
[Using the identity (x + a) (x + b) = x2 +
(a + b)x + ab. Here a = 4, b = 10]
= x2 + 14x + 40
Question 70:
Use the suitable identity to find the following products:
(x + 8) (x – 10)
Answer:
(x + 8) (x – 10) =x2 + {8 + ( – 10)} x + 8 × ( – 10) =x2 – 2x – 80 [Using the identity (x + a) (x + b)= x2 + (a + b) x + ab. Here a = 8, b = – 10]
Question 71:
Use the suitable identity to find the following products:
(3x + 4) (3x – 5)
Answer:
(3x + 4) (3x – 5)
Put 3x = y, we get:
(y + 4) (y – 5)
= y2 + {4 + ( – 5)} y + 4 (–5)
[Using the identity(x + a) (x + b) = x2
+ (a + b) x + ab. Here a = 4, b = – 5]
= y2 – y – 20
= (3x)2 – 3x – 20 [ 3x = y]
= 9x2 – 3x – 20
Question 72:
Use the suitable identity to find the following products:
Answer:
Question 73:
Use the suitable identity to find the following products:
(3 – 2x) (3 + 2x)
Answer:
(3 – 2x) (3 + 2x)
or = – (2x – 3) (2x + 3)
or = – (2x + 3) (2x – 3)
Put 2x = y, we get:
– (y + 3) (y – 3)
= – [y2 + (3 – 3)y + 3 ( – 3)]
[Using the identity (x + a) (x + b) = x2 +
(a + b)x + ab. Here a = 3, b = – 3]
= – (y2 + 0y – 9)
= – (y2 – 9)
= – [(2x)2 – 9]
(where 2x = y as substituted above)
= – (4x2 – 9) = 9 – 4x2
Question 74:
Evaluate the following products without multiplying directly:
103 × 107
Answer:
103 × 107
= (100 + 3) (100 + 7)
[Writing 103 as 100 + 3 and
107 as 100 + 7]
= (100)2 + (3 + 7) 100 + 3 × 7
= 10000 + 10 × 100 + 21
= 10000 + 1000 + 21
= 11021 [Using the identity (x + a) (x + b)
= x2 + (a + b)x + ab. Here
x = 100, a = 3, b = 7]
Question 75:
Evaluate the following products without multiplying directly:
95 × 96
Answer:
95 × 96 = (100 – 5) (100 – 4)
[Writing 95 as 100 – 5 and 96 as 100 – 4]
= (100)2 + [( – 5) + ( – 4)] 100 + ( – 5) ( – 4)
[Using the identity (x + a) (x + b) = x2 +
(a + b) x + ab. Here x = 100, a = – 5, b = – 4]
= 10000 + (– 9) × 100 + 20
= 10000 – 900 + 20
= 9120
Question 76:
Evaluate the following products without multiplying directly:
104 × 96
Answer:
104 × 96
= (100 + 4) (100 – 4)
[Writing 104 as 100 + 4 and 96 as 100 – 4]
(100)2 – (4)2
[Using identity a2 – b2 = (a + b) (a – b).
Here a = 100 and b = 4]
= 10000 – 16
= 9984
Question 77:
Factorise the following using appropriate identities:
9x2 + 6xy + y2
Answer:
9x2 + 6xy + y2
=(3x)2 + 2(3x)y + y2
=(3x + y)2
[Using identity (a + b)2 = a2 + 2ab + b2.
Here a = 3x and b = y]
Question 78:
Factorise the following using appropriate identities:
4y2 – 4y + 1
Answer:
4y2 – 4y + 1
= (2y)2 – 2(2y) 1 + 12
= (2y – 1)2
[Using the identity (a – b)2 = a2 – 2ab + b2.
Here a = 2y and b = 1]
Question 79:
Factorise the following using appropriate identities:
Answer:
Question 80:
Expand each of the following, using suitable identities:
(x + 2y + 4z)2
Answer:
(x + 2y + 4z)2
Comparing the given expression with
(a + b + c)2 we find that a = x, b = 2y
and c = 4z
Therefore using the identity
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc +
2ca
we write (x + 2y + 4z)2 = x2 + (2y)2 + (4z)2
+
2x(2y) + 2(2y) (4z) + 2(4z)x
= x2 + 4y2 + 16z2 + 4xy + 16yz + 8xz
Question 81:
Expand each of the following, using suitable identities:
(2x – y + z)2
Answer:
(2x – y + z)2
= [2x + ( – y) + z]2
Comparing the given expression with
(a + b + c)2 we find that a = 2x, b = – y
and c = z.
Therefore using the identity
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc +
2ca
we write
{(2x + (– y) + z)2} = (2x)2 + (–y)2 + z2
+ 2(2x) (– y) + 2( –y) z + 2z (2x)
= 4x2 + y2 + z2 – 4xy – 2yz + 4zx
Question 82:
Expand each of the following, using suitable identities:
(– 2x + 3y + 2z)2
Answer:
(– 2x + 3y + 2z)2
Comparing the given expression with
(a + b + c)2 we find that a = – 2x, b = 3y and
c = 2z
Therefore using the identity
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc +
2ca
we write
(– 2x + 3y + 2z)2 = {(– 2x)2 + (3y)2 + (2z)2
+ 2( – 2x) (3y) + 2 (3y) (2z) + 2(2z) (– 2x)}
= 4x2 + 9y2 + 4z2 – 12xy + 12yz – 8zx.
Question 83:
Expand each of the following, using suitable identities:
(3a – 7b – c)2
Answer:
(3a – 7b – c)2
= [(3a) + (–7b) + (–c)]2
Comparing the given expression with
(a + b + c)2 we find that a = 3a, b = –7b, and
c = –c
Using the identity
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc +
2ca
we get:
[3a + (–7b) + (–c)]2 = (3a)2 + (–7b)2 +
(–c)2
+ 2 (3a) (–7b) + 2 (–7b) (–c) + 2(–c) (3a)
= 9a2 + 49b2 + c2 – 42ab + 14bc – 6ca
Question 84:
Expand each of the following, using suitable identities:
(– 2x + 5y – 3z)2
Answer:
(–2x + 5y – 3z)2 = [–2x + 5y + (–3z)]2
Comparing the given expression with
(a + b + c)2 we find that a = –2x, b = 5y and c = –3z
Therefore using the identity
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc +
2ca
we write
[–2x + 5y + (–3z)]2
= (–2x)2 + (5y)2 + (–3z)2 + 2(–2x) (5y)
+ 2(5y) (–3z) + 2 (–3z) (–2x)
= 4x2 + 25y2 + 9z2 – 20xy – 30yz + 12zx
Question 85:
Expand each of the following, using suitable identities:
Answer:
Question 86:
Factorise:
4x2 + 9y2 + 16z2 + 12xy – 24yz – 16xz
Answer:
Question 87:
Factorise:
Answer:
Question 88:
Write the following cube in expanded form:
(2x + 1)3
Answer:
(2x + 1)3
Compare the expression (2x + 1)3 with (a + b)3,
we find that a = 2x, b = 1
Therefore using the identity
(a + b)3 = a3 + b3 + 3ab (a + b)
we have:
(2x + 1)3 = (2x)3 + (1)3 + 3(2x) 1 (2x + 1)
= 8x3 + 1 + 12x2 + 6x
= 8x3 + 12x2 + 6x + 1
[Re-arranging in descending power of x.]
Question 89:
Write the following cube in expanded form:
(2a – 3b)3
Answer:
(2a – 3b)3
Comparing the expression (2a – 3b)3
with (x – y)3 we find that x = 2a, y = 3b
Therefore using the identity
(x – y)3=x3 – y3 – 3xy (x – y), we get:
(2a – 3b)3=(2a)3 – (3b)3 –3 (2a) (3b) (2a – 3b)
=8a3 – 27b3 – 36a2b + 54ab2
Question 90:
Write the following cube in expanded form:
Answer:
Question 91:
Write the following cube in expanded form:
Answer:
Question 92:
Evaluate the following using suitable identities:
(99)3
Answer:
(99)3 = (100 – 1)3
= (100)3 – 13 – 3(100) 1(100 – 1)
[Using the identity
(a – b)3 = a3 – b3 – 3ab (a – b)]
= 1000000 – 1 – 30000 + 300
= 970299
Question 93:
Evaluate the following using suitable identities:
(102)3
Answer:
(102)3= (100 + 2)3
= (100)3 + 23 + 3(100) (2) (100 + 2)
[Using the identity
(a + b) 3 = a3 + b3 + 3ab (a + b)]
= 1000000 + 8 + 60000 + 1200
= 1061208
Question 94:
Evaluate the following using suitable identities:
(998)3
Answer:
(998)3= (1000 – 2)3
= (1000)3 – 23 – 3(1000) (2)(1000 – 2)
[Using the identity
(a – b)3 = a3 – b3 – 3ab (a – b)]
= 1000000000 – 8 – 6000000 + 12000
= 1000012000 – 6000008
= 994011992
Question 95:
Factorise each of the following:
8a3 + b3 + 12a2b + 6ab2
Answer:
8a3 + b3 + 12a2b + 6ab2
= (2a)3 + b3 + 3 (2a) b (2a + b)
= (2a + b)3
[Using the identity
(x + y)3 = x3 + y3 + 3xy (x + y).
Here x = 2a and y = b]
Question 96:
Factorise each of the following:
8a3 – b3 – 12a2b + 6ab2
Answer:
8a3 – b3 – 12a2b + 6ab2
= (2a)3 – b3 – 3 (2a) b (2a – b)
= (2a – b)3
[Using the identity
(x – y)3 = x3 – y3 – 3xy (x – y).
Here x = 2a and y = b]
Question 97:
Factorise each of the following:
27 – 125a3 – 135a + 225a2
Answer:
27 – 125a3 – 135a + 225a2
= (3)3 – (5a)3 – 3 (3) (5a) (3 – 5a)
= (3 – 5a)3
[Using the identity
(x – y)3 = x3 – y3 – 3xy (x – y).
Here x = 3, y = 5a]
Question 98:
Factorise each of the following:
64a3 – 27b3 – 144a2b + 108ab2
Answer:
64a3 – 27b3 – 144a2b + 108ab2
= (4a)3 – (3b)3 – 3(4a) (3b)
(4a – 3b)
= (4a – 3b)3
[Using the identity
(x – y)3 = x3 – y3 – 3xy (x – y).
Here x = 4a, y = 3b]
Question 99:
Factorise each of the following:
Answer:
Question 100:
Verify: x3 + y3 = (x + y) (x2 – xy + y2)
Answer:
Question 101:
Verify: x3 – y3 = (x – y) (x2 + xy + y2)
Answer:
Question 102:
Factorise each of the following:
27y3 + 125z3
Answer:
27y3 + 125z3
= (3y)3 + (5z)3
= (3y + 5z) [(3y)2 – (3y) (5z) + (5z)2]
[Using identity
a3 + b3 = (a + b) (a2 – ab + b2)
Here a = 3y, b = 5z]
= (3y + 5z) (9y2 – 15yz + 25z2)
Question103 :
Factorise each of the following:
64m3 – 343n3
Answer:
64m3 – 343n3
= (4m)3 – (7n)3
= (4m – 7n) [(4m)2 + (4m) (7n) + (7n)2]
[Using identity
a3 – b3 = (a – b) (a2 + ab + b2).
Here a = 4m, b = 7n]
= (4m – 7n) (16m2 + 28mn + 49n2)
Question 104:
Factorise: 27x3 + y3 + z3 – 9xyz
Answer:
Question 105:
Answer:
Question 106:
If x + y + z = 0, show that x3 + y3 + z3 = 3xyz
Answer:
Question 107:
Without actually calculating the cubes, find the value of the following:
(–12)3 + (7)3 + (5)sup>3
Answer:
Let a = –12, b = 7 and c = 5
When a + b + c = 0
then a3 + b3 + c3 = 3abc
Here a + b + c = – 12 + 7 + 5 = 0
(–12)3 + (7)3 + (5)3
= 3(–12) (7) (5)
= –1260
Question 108:
Without actually calculating the cubes, find the value of the following:
(28)3 + (–15)3 + (–13)3
Answer:
Let a = 28, b = –15 and c = –13
Now a + b + c = 28 + (–15) + (–13)
= 28 – 15 – 13
= 28 – 28
= 0
a3 + b3 + c3 = 3abc
(28)3 + (–15)3 + (–13)3
= 3(28) (–15) (–13)
= 16380
Question 109:
Give possible expressions for the length and breadth of the following rectangle, in which
area is given:
Area: 25a2 – 35a + 12
Answer:
Area of rectangle
= 25a2 – 35a + 12 (given)
length × breadth = 25a2 – 15a – 20a + 12
= 5a (5a – 3) – 4 (5a – 3)
= (5a – 4) (5a – 3)
If length = (5a – 4)
then breadth = 5a – 3
and If length = 5a – 3
then breadth = (5a – 4)
Question 110:
Give possible expressions for the length and breadth of the following rectangle, in which
area is given:
Area: 35y2 + 13y – 12
Answer:
Area of rectangle = 35y2 + 13y – 12
length × breadth = 35y2 + 28y – 15y – 12
= 7y(5y + 4) – 3(5y + 4)
Length × Breadth= (5y + 4) (7y – 3)
If length = 5y + 4
then breadth = 7y – 3
and If length = 7y – 3
then breadth = 5y + 4
Question 111:
What are the possible expressions for the dimensions of the cuboids whose volumes are given
below?
Volume: 3x2 – 12x
Answer:
Volume of cuboid = 3x2 – 12x (given)
Length × Breadth × Height = 3x (x – 4)
One possible dimensions of cuboid are
3, x and x – 4
Question 112:
What are the possible expressions for the dimensions of the cuboids whose volumes are given
below?
Volume: 12ky2 + 8ky – 20k
Answer:
Volume of cuboid = 12ky2 + 8ky – 20k
Length × Breadth × Height
= 4k (3y2 + 2y – 5)
= 4k [3y2 + 5y – 3y – 5]
= 4k [y(3y + 5) – 1 (3y + 5)]
= 4k [(3y + 5) (y – 1)]
Length × Breadth × Height
= 4k (3y + 5) (y – 1)
One possible dimensions of cuboid are
4k, (3y + 5) and (y –1).