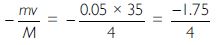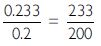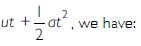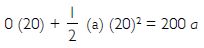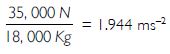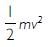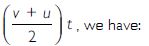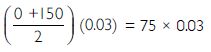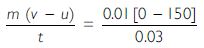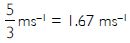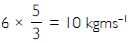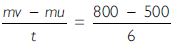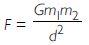Question 1:
Which of the following has more inertia?
(a) A rubber ball and a stone of the same size
(b) A bicycle and a train
(c) A five-rupee coin and a one-rupee coin
Answer:
Inertia is directly proportional to the mass, or the more the mass, more is the inertia.
Hence,
(a) A stone has more inertia than a rubber ball.
(b) A train has more inertia than a bicycle.
(c) A five-rupee coin has more inertia than one a rupee-coin.
Question 2:
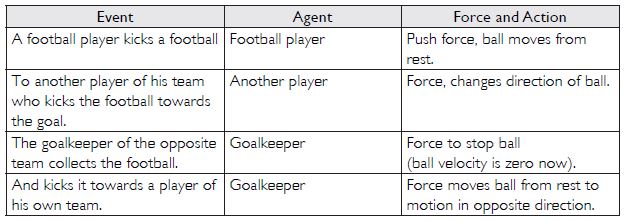
In the following example, try to identify the number of times the velocity of the ball
changes:
‘A football player kicks a football to another player of his team who kicks the football
towards the goal. The goalkeeper of the opposite team collects the football and kicks it
towards a player of his own team.’
Also identify the agent supplying the force in each case.
Answer:
We need to apply first law of motion and identify what force is applied which changes the
velocity (state i.e. rest, direction, motion) of the ball. A force when applied can produce
acceleration in body.
Question 3:
Explain why some of the leaves may get detached from the tree if we vigorously shake its branch.
Answer:
When we shake the branch of a tree, the branch comes in motion and the leaves remain at rest due to inertia of rest and get detached from the moving branch.
Question 4:
Why do you fall in the forward direction when brakes are applied on a moving bus and fall backward when it accelerates from rest?
Answer:
When the bus is moving forward, our whole body is moving forward. When brakes are applied,
the parts of our body touching the bus (e.g. feet) come to rest and the upper body part not
in contact with the bus continues to move forward due to the inertia of motion. Hence, we
fall in forward direction.
When bus accelerates from rest, the lower part of our body (e.g. feet) comes in motion while
the upper part is still at rest due to inertia of rest and tends to remain at the same
position, thereby making us fall in the backward direction.
Question 5:
If action is always equal to reaction, explain how a horse can pull a cart?
Answer:
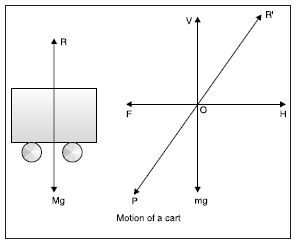
Various forces acting on the horse and the cart are:
(i) Weight Mg of the cart is balanced by reaction R on the cart.
(ii) Horse pushes the cart with a force P in the direction OP backward and gets a reaction
R’ along OR’.
(iii) Reaction R’ can be resolved in two rectangular components; H in the horizontal
direction and V in the vertical direction. Here, the vertical component of reaction R’ i.e.,
V balances the weight of horse acting vertically downwards.
Two forces left unbalanced are horizontal component H in the forward direction and force of
friction F between the cart and the ground in opposite direction.
If H < F, the force of limiting friction, the cart will not move.
If H is slightly greater than F, the cart will move.
If H is very much greater than F, the cart will be accelerated in the direction of
H.
If H = F after the start of motion, then the cart will move with constant velocity.
Question 6:
Explain why it is difficult for a fireman to hold a hose, which ejects large amount of water at a high velocity.
Answer:
When water is ejected in the forward direction from a hose with a force (action), then water exerts a reaction on the hose in the backward direction. Due to backward movement of the hose, it is difficult for the fireman to hold the hose.
Question 7:
From a rifle of mass 4 kg, a bullet of mass 50 g is fired with an initial velocity of 35 ms-1. Calculate the initial recoil velocity of the rifle.
Answer:
Here M = 4 kg; m = 50 g = 0.05 kg; V =?, u = 35 ms-1.
Using M V + mv = 0 or MV = -mv
V =
V = - 0.4375 ms-1 = - 43.75 cms-1
Negative sign indicates that the gun moves in a direction opposite to that of the bullet.
Question 8:
Two objects of masses 100 g and 200 g are moving along the same line and direction with velocities of 2 ms-1 and 1 ms-1 respectively. They collide and after the collision, the first object moves with a velocity of 1.67 ms-1. Determine the velocity of the second object.
Answer:
m1 = 100 g = 0.1 kg; m2 = 200 g = 0.2 kg;
u1 = 2 ms-1; u2 = 1 ms-1; v1 = 1.67
ms-1; v2 = ?
Now m1u1 + m2u2 = m1v1 +
m2v1
0.1 x 2 + 0.2 x 1 = 0.1 x 1.67 + 0.2 v2
0.4 = 0.167 + 0.2 v2
0.2 v2 = 0.4 - 0.167 = 0.233
v2 =
Question 9:
An object experiences zero net external unbalanced force. Is it possible for the object to be travelling with a non-zero velocity? If yes, state the conditions that must be placed on the magnitude and direction of the velocity. If no, provide a reason.
Answer:
Yes, motion is possible even when zero net unbalanced force is applied. The condition is that the body should initially be in motion and a constant force, exactly equal to the force of limiting friction, should continuously be applied in forward direction in the direction of motion.
Question 10:
When a carpet is beaten with a stick, the dust comes out of it. Explain.
Answer:
When a carpet is beaten with a stick, the carpet comes into motion. Due to inertia of rest, dust particles tend to remain at rest and fall down.
Question 11:
Why is it advised to tie any luggage kept on the roof of a bus with rope?
Answer:
If luggage is not tied with a rope to the body of the bus, it will move backward due to inertia of rest when the bus starts moving and will move forward due to inertia of motion when the bus stops.
Question 12:
A batsman hits a cricket ball which then rolls on a level ground. After covering a short
distance, the ball comes to rest. The ball slows down and stops because
(a) the batsman did not hit the ball hard enough.
(b) velocity is proportional to the force exerted on the ball.
(c) there is a force on the ball opposing the motion.
(d) there is no unbalanced force on the ball, so the ball would try to come at rest.
Answer:
Correct answer is (c). There is a force of friction on the ball in the direction opposite to that of motion.
Question 13:
A truck starts from rest and rolls down a hill with a constant acceleration. It travels a distance of 400 m in 20 s. Find its acceleration. Find the force on it if its mass is 7 metric tonnes. (1 tonne = 1,000 kg)
Answer:
u = 0; a =? ; s = 400 m; t = 20 s
Using s =
400 =
a = 2 ms-2
m = 7,000 kg; a = 2 ms-2, F = ?
F = ma = 7,000 x 2
F = 14,000 N
Question 14:
A stone of 1 kg is thrown with a velocity of 20 ms-2 across the frozen surface of a lake and comes to rest after travelling a distance of 50 m. What is the force of friction between the stone and the ice?
Answer:
m = 1 kg; u = 20 ms-2; v = 0; s = 50 m; a = ?
Using v2 - u2 = 2as, we have:
(0)2 - (20)2 = 2 (a) 50
a = - 4 ms-2
F = ma = 1 (- 4)
F = - 4 N
Therefore, a force of 4 N is acting in a direction opposite to the direction of motion of
stone.
Question 15:
An 8,000 kg engine pulls a train of 5 wagons, each of 2,000 kg along a horizontal track. If
the engine exerts a force of 40,000 N and track offers a force of friction of 5,000 N, then
calculate:
(a) the net accelerating force and
(b) the acceleration of the train
Answer:
Given :
Force of engine = 40,000 N
Force of friction = 5,000 N
Mass of engine = 8,000 kg, Mass of 1 wagon = 2,000 kg
Total mass = mass of engine + mass of 5 wagons
= 8,000 kg + 5 x 2,000 kg
= 18,000 kg
(a) Net accelerating force
= Force exerted by engine - Force of friction
= 40,000 N - 5,000 N
= 35,000 N
(b) Acceleration of the train
F = ma
35,000 N = Total mass x a
or 35,000 N = 18,000 kg x a
\ a =
Question 16:
An automobile vehicle has a mass of 1,500 kg. What must be the force between the vehicle and the road if the vehicle is to be stopped with negative acceleration of 1.7 ms-2?
Answer:
m = 1,500 kg; a = - 1.7 ms-2
F = m a = (1,500) (-1.7) = - 2,550 N
Backward force = 2,550 N (in a direction opposite to the motion of vehicle.)
Question 17:
What is the momentum of an object of mass m moving with velocity v?
- (m v)2
- mv2
-
- mv
Answer:
(d) is correct. Momentum = mv
Question 18:
Using a horizontal force of 200 N, we intend to move a wooden cabinet across a floor with a constant velocity. What is the friction force that will be exerted on the cabinet?
Answer:
When no acceleration is to be produced (that is the body is to be moved with constant velocity), the net force has to be zero. The force of friction should be equal and opposite to the force applied i.e., it has to be 200 N.
Question 19:
Two objects, each of mass 1.5 kg, are moving in the same straight line but in the opposite directions. The velocity of each object is 2.5 ms-1 before the collision during which they stick together. What will be the velocity of combined object after collision?
Answer:
Here m1 = m2 = 1.5 kg; u1 = 2.5 ms-1;
u1 = -2.5 ms-2
Combined mass, M = m1 + m2 = 1.5 + 1.5 = 3 kg; V = ?
Since momentum is conserved,
\ m1u1 + m2u2 = (m1 + m2)
V
1.5 x 2.5 + 1.5 (-2.5) = 3V
3V = 0 or V = 0 ms-1
Therefore, the combined object will be at rest.
Question 20:
According to the third law of motion when we push an object, the object pushes back on us with an equal and opposite force. If the object is a massive truck parked along the road side, it will probably not move. A student justifies this by answering that the two equal and opposite forces cancel each other. Comment on this logic and explain why the truck did not move.
Answer:
The student has not given the correct justification because the forces of action and reaction never act on the same body. The truck will move only when the applied force is greater than the force of friction.
Question 21:
A hockey ball of mass 200 g travelling at 10 ms-1 is struck by a hockey stick so as to return it along its original path with a velocity of 5 ms-1. Calculate the change in momentum occurred in the motion of hockey ball by the force applied by hockey stick.
Answer:
m = 200 g = 0.2 kg; u = 10 ms-1; v = - 5 ms-1
Change in momentum = Initial momentum - Final momentum
= 0.2 (10) - 0.2 (-5) = 2 + 1
= 3 kgms-1
Question 22:
A bullet of mass 10 g travelling horizontally with a velocity of 150 ms-1 strikes a stationary wooden block and come to rest in 0.03 s. Calculate the distance of penetration of the bullet into the block. Also, calculate the magnitude of force exerted by the wooden block on the bullet.
Answer:
m = 10 g = 0.01 kg; u = 150 ms-1;
v = 0 ms-1; t = 0.03 s; s = ?
Using s =
s =
s = 2.25 m
Using F =
F = - 50 N
Negative sign shows that the force is applied in the opposite direction of the motion of the
bullet.
Question 23:
An object of mass 1 kg travelling in a straight line with a velocity of 10 ms-1 collides with and sticks to a stationary wooden block of mass 5 kg. Then they both move off together in the same straight line. Calculate the total momentum just before the impact and just after the impact. Also, calculate the velocity of the combined object.
Answer:
m1 = 1 kg; u1 = 10 ms-1; m2 = 5 kg; u2
= 0;
Combined mass, M = m1 + m2 = 1 + 5 = 6 kg
Combined velocity = V
Using principle of conservation of momentum, we have
m1u1 + m2u2 = MV
1 x 10 + 5 x 0 = 6V
V =
Momentum before impact = m1u1 + m2u2
= 1 x 10 + 5 x 0 = 10 kgms-1
Momentum after impact = MV =
Question 24:
An object of mass 100 kg is accelerated uniformly from a velocity of 5 ms-1 to 8 ms-1 in 6 s. Calculate the initial and final momentum of the object. Also, find the magnitude of force exerted on the object.
Answer:
Initial momentum = mu = 100 x 5 = 500 kgms-1
Final momentum = mv = 100 x 8 = 800 kgms-1
F =
F = 50 N
Question 26:
Akhtar, Kiran and Rahul were riding in a motor car that was moving with a high velocity on an expressway when an insect hit the windshield and got stuck there. Akhtar and Kiran started pondering over the situation. Kiran suggested that the insect suffered a great change in momentum as compared to the change in momentum of the motor car (because the change in the velocity of the insect was much more than that of the motor car). Akhtar said that since the motor car was moving with a larger velocity, it exerted a larger force on the insect. As a result, the insect died. Rahul, while putting in an entirely new explanation, said that both the motor car and the insect experienced the same force and a change in their momentum. Comment on these suggestions.
Answer:
I agree with Rahul. The change in momentum as well as the rate of change of momentum (and hence, force) in both the cases is the same. Since, mass of the car is much larger than that of the insect; therefore change of velocity of the car is too small to be noticed. Due to the very small mass of the insect, its change of velocity is too large to crush it to death.
Question 27:
How much momentum will a dumb-bell of mass 10 kg transfer to the floor if it falls from a height of 80 cm? Take its downward acceleration to be 10 ms-2.
Answer:
u = 0 ms-1; v =? ; a = 10 ms-2; s = 80 cm = 0.8 m
Using v2 - u2 = 2as, we have:
v2 - (0)2 = 2 (10) (0.8) = 16
v = 4 ms-1
Momentum transferred = m v = 10 x 4 = 40 kgms-1.
Question 28:
State the universal law of gravitation.
Answer:
Newton’s universal law of gravitation states that every object in the universe attracts every
other object with a force which is directly proportional to the product of their masses and
inversely proportional to the square of the distance between them.
If m1 and m2 are the masses of two objects lying at a distance d
apart, then force F between them is :
where, G is a constant called universal gravitational constant.