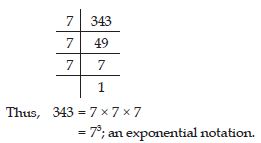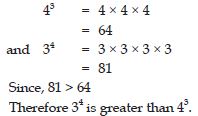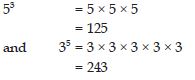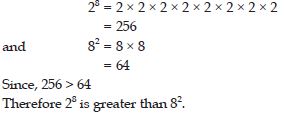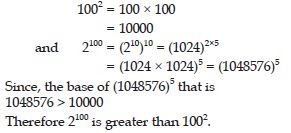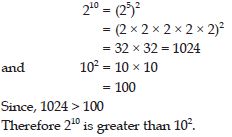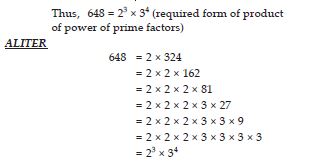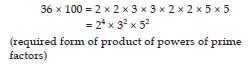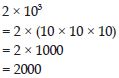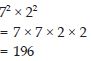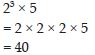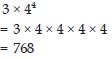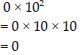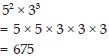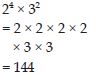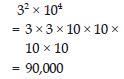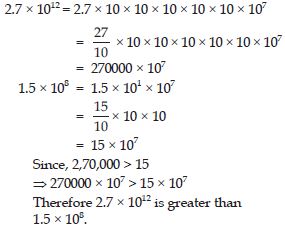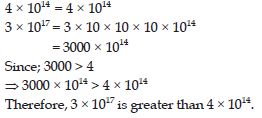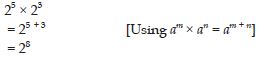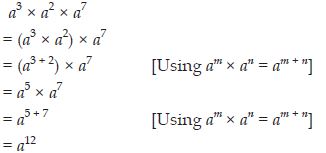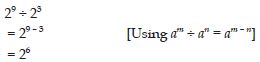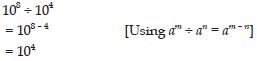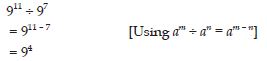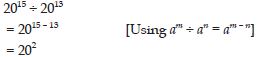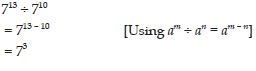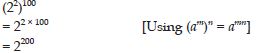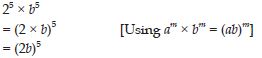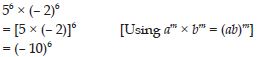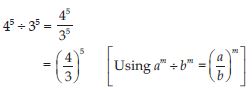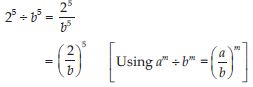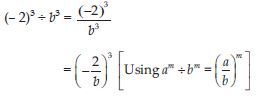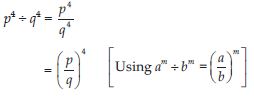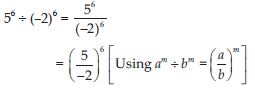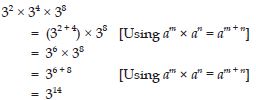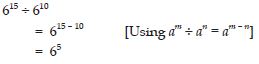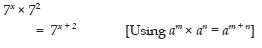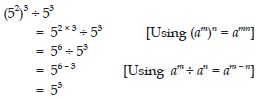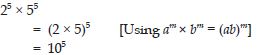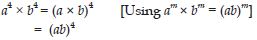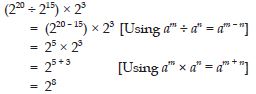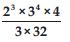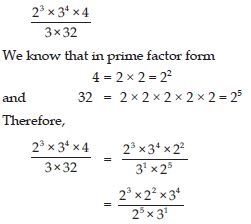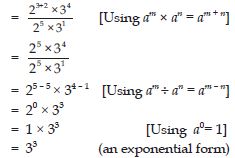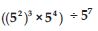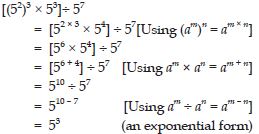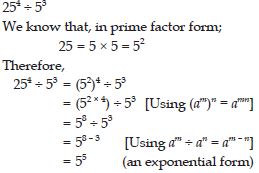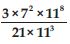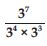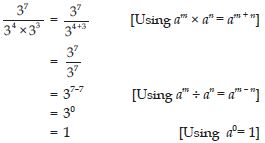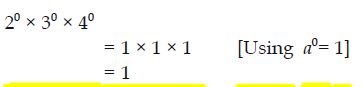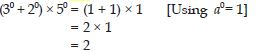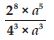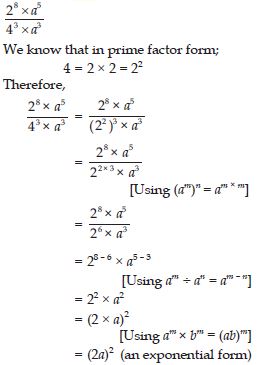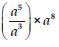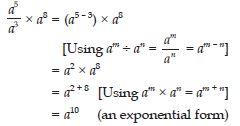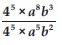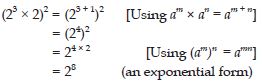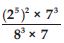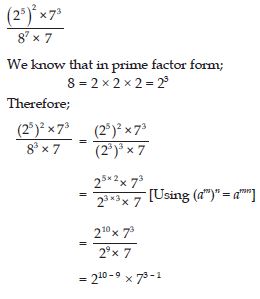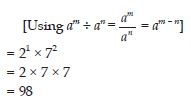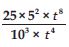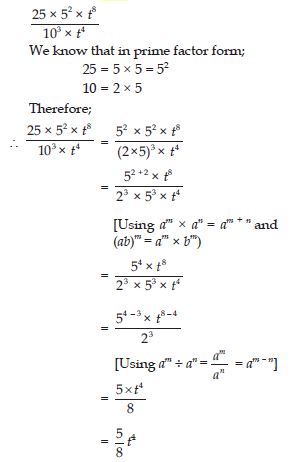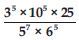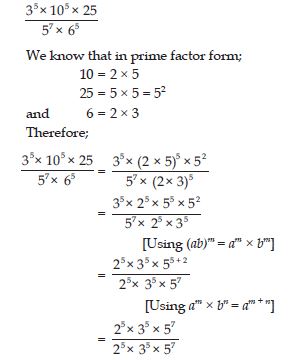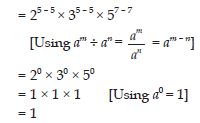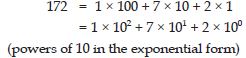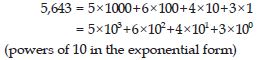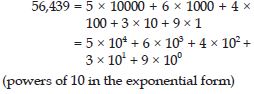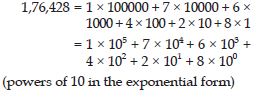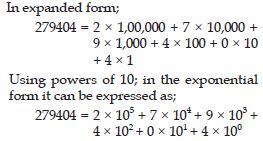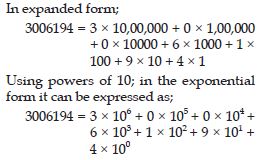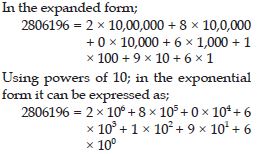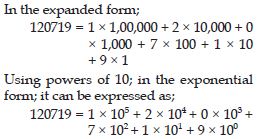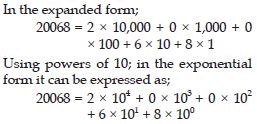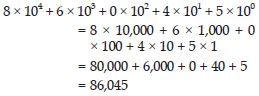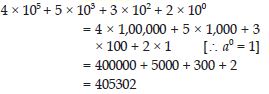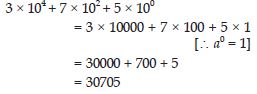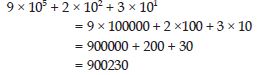NCERT Solutions for Class 7 Mathematics Chapter 12 - Exponents and Powers

Question 1:

Give five examples, where a number is expressed in exponential form. Also identify the base and exponent in each case.

Question 2:

Express:
729 as a power of 3

Question 3:

Express:
128 as power of 2

Question 4:

Express:
343 as power of 7

Question 5:

Find the value of:
2⁶

Question 6:

Find the value of:
9³

Question 7:

Find the value of:
11²

Question 8:

Find the value of:
5⁴

Question 9:

Express the following in exponential form:
6 × 6 × 6 × 6

Question 10:

Express the following in exponential form:
t × t

Question 11:

Express the following in exponential form:
b × b × b × b

Question 12:

Express the following in exponential form:
5 × 5 × 7 × 7 × 7

Question 13:

Express the following in exponential form:
2 × 2 × a × a

Question 14:

Express the following in exponential form:
a × a × a × c × c × c × c × d

Question 15:

Express each of the following numbers using exponential notation:
512

Question 16:

Express each of the following numbers using exponential notation:
343

Question 17:

Express each of the following numbers using exponential notation:
729

Question 18:

Express each of the following numbers using exponential notation:
3125

Question 19:

Indentify the greater number, wherever possible, in each of the following?
4³ or 3⁴

Question 20:

Indentify the greater number, wherever possible, in each of the following?
5³ or 3⁵

Question 21:

Indentify the greater number, wherever possible, in each of the following?
2⁸ or 8²

Question 22:

Indentify the greater number, wherever possible, in each of the following?
100² or 2¹⁰⁰

Question 23:

Indentify the greater number, wherever possible, in each of the following?
2¹⁰ or 10²

Question 24:

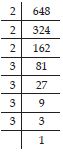
Express each of the following as product of powers of their prime factors:
648

Question 25:

Express each of the following as product of powers of their prime factors:
405

Question 26:

Express each of the following as product of powers of their prime factors:
540

Question 27:

Express each of the following as product of powers of their prime factors:
3600

Question 28:

Simplify:
2 × 10³

Question 29:

Simplify:
7² × 2²

Question 30:

Simplify:
2³ × 5

Question 31:

Simplify:
3 × 4⁴

Question 32:

Simplify:
0 × 10²

Question 33:

Simplify:
5² × 3²

Question 34:

Simplify:
2⁴ × 3²

Question 35:

Simplify:
3² × 10⁴

Question 36:

Simplify:
(– 4)³

Question 37:

Simplify:
(– 3) × (– 2)³

Question 38:

Simplify:
(– 3)² × (– 5)²

Question 39:

Simplify:
(– 2)³ × (– 10)³

Question 40:

Compare the following numbers:
2.7 × 10¹²; 1.5 × 10⁸

Question 41:

Compare the following numbers:
4 × 10¹⁴; 3 × 10¹⁷

Question 42:

Simplify and write in exponential form:
2⁵ × 2³

Question 43:

Simplify and write in exponential form:
p³ × p²

Question 44:

Simplify and write in exponential form:
4³ × 4²

Question 45:

Simplify and write in exponential form:
a³ × a² × a⁷

Question 46:

Simplify and write in exponential form:
5³ × 5⁷ × 5¹²

Question 47:

Simplify and write in exponential form:
(– 4)¹⁰⁰ × (– 4)²⁰

Question 48:

Simpify and write in exponential form:
2⁹ ÷ 2³

Question 49:

Simpify and write in exponential form:
10⁸ ÷ 10⁴

Question 50:

Simpify and write in exponential form:
9¹¹ ÷ 9⁷

Question 51:

Simpify and write in exponential form:
20¹⁵ ÷ 20¹³

Question 52:

Simpify and write in exponential form:
7¹³ ÷ 7¹⁰

Question 53:

Simplify and write the answer in exponential form:
(6²)⁴

Question 54:

Simplify and write the answer in exponential form:
(2²)¹⁰⁰

Question 55:

Simplify and write the answer in exponential form:
(7⁵⁰)²

Question 56:

Simplify and write the answer in exponential form:
(5³)⁷

Question 57:

4³ × 2³

Question 58:

2⁵ × b⁵

Question 59:

a² × t²

Question 60:

5⁶ × (– 2)⁶

Question 61:

(– 2)⁴ × (– 3)⁴

Question 62:

4⁵ ÷ 3⁵

Question 63:

2⁵ ÷ b⁵

Question 64:

(– 2)³ ÷ b³

Question 65:

p⁴ ÷ q⁴

Question 66:

5⁶ ÷ (– 2)⁶

Question 67:

Using laws of exponents, simplify and write the answer in exponential form:
3² × 3⁴ × 3⁸

Question 68:

Using laws of exponents, simplify and write the answer in exponential form:
6¹⁵ ÷ 6¹⁰

Question 69:

Using laws of exponents, simplify and write the answer in exponential form:
a³× a²

Question 70:

Using laws of exponents, simplify and write the answer in exponential form:
7^x × 7²

Question 71:

Using laws of exponents, simplify and write the answer in exponential form:
(5²)³ ÷ 5³

Question 72:

Using laws of exponents, simplify and write the answer in exponential form:
2⁵ × 5⁵

Question 73:

Using laws of exponents, simplify and write the answer in exponential form:
a⁴ × b⁴

Question 74:

Using laws of exponents, simplify and write the answer in exponential form:
(3⁴)³

Question 75:

Using laws of exponents, simplify and write the answer in exponential form:
(2²⁰ ÷ 2¹⁵) × 2³

Question 76:

Using laws of exponents, simplify and write the answer in exponential form:
8^t ÷ 8²

Question 77:

Simplify and express each of the following in exponential form:

Question 78:

Simplify and express each of the following in exponential form:

Question 79:

Simplify and express each of the following in exponential form:
25⁴ ÷ 5³

Question 80:

Simplify and express each of the following in exponential form:

Question 81:

Simplify and express each of the following in exponential form:

Question 82:

Simplify and express each of the following in exponential form:
2⁰ + 3⁰ + 4⁰

Question 83:

Simplify and express each of the following in exponential form:
2⁰ × 3⁰ × 4⁰

Question 84:

Simplify and express each of the following in exponential form:
(3⁰ + 2⁰) × 5⁰

Question 85:

Simplify and express each of the following in exponential form:

Question 86:

Simplify and express each of the following in exponential form:

Question 87:

Simplify and express each of the following in exponential form:

Question 88:

Simplify and express each of the following in exponential form:

Question 89:

10 × 10¹¹ = 100¹¹

1. TRUE
2. FALSE

Question 90:

2³ > 5²

1. TRUE
2. FALSE

Question 91:

2³ × 3² = 6⁵

1. TRUE
2. FALSE

Question 92:

3⁰ = (1000)⁰

1. TRUE
2. FALSE

Question 93:

Express each of the following as a product of prime factors only in exponential form:
108 × 192

Question 94:

Express each of the following as a product of prime factors only in exponential form:
270

Question 95:

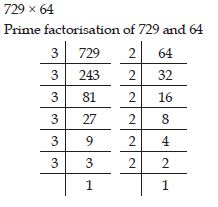
Express each of the following as a product of prime factors only in exponential form:
729 × 64

Question 96:

Express each of the following as a product of prime factors only in exponential form:
768

Question 97:

Simplify:

Question 98:

Simplify:

Question 99:

Simplify:

Question 100:

Expand by expressing powers of 10 in the exponential form:
172

Question 101:

Expand by expressing powers of 10 in the exponential form:
5,643

Question 102:

Expand by expressing powers of 10 in the exponential form:
56,439

Question 103:

Expand by expressing powers of 10 in the exponential form:
1,76, 428

Question 104:

Write the following numbers in the expanded forms:
279404

Question 105:

Write the following numbers in the expanded forms:
3006194

Question 106:

Write the following numbers in the expanded forms:
2806196

Question 107:

Write the following numbers in the expanded forms:
120719

Question 108:

Write the following numbers in the expanded forms:
20068

Question 109:

Find the number from each of the following expanded forms:
8 × 10⁴ + 6 × 10³ + 0 × 10² + 4 × 10¹ + 5 × 10⁰

Question 110:

Find the number from each of the following expanded forms:
4 × 10⁵ + 5 × 10³ + 3 × 10² + 2 × 10⁰

Question 111:

Find the number from each of the following expanded forms:
3 × 10⁴ + 7 × 10² + 5 × 10⁰

Question 112:

Find the number from each of the following expanded forms:
9 × 10⁵ + 2 × 10² + 3 × 10¹

Question 113:

Express the following numbers in standard form:
5,00,00,000

Question 114:

Express the following numbers in standard form:
70,000,00

Question 115:

Express the following numbers in standard form:
3,18,6500,000

Question 116:

Express the following numbers in standard form:
3,90,878

Question 117:

Express the following numbers in standard form:
39087.8

Question 118:

Express the following numbers in standard form:
3908.78

Question 119:

Express the number appearing in the following statements in standard form.
The mean distance between Earth and Moon is 384,000,000 m.

Question 120:

Express the number appearing in the following statements in standard form.
Speed of light in vacuum is 300,000,000 m/s.

Question 121:

Express the number appearing in the following statements in standard form.
Diameter of the Earth is 1,27,56,000 m.

Question 122:

Express the number appearing in the following statements in standard form.
Diameter of the Sun is 1,400,000,000 m.

Question 123:

Express the number appearing in the following statements in standard form.
In a galaxy there are on an average 100,000,000,000 stars.

Question 124:

Express the number appearing in the following statements in standard form.
The universe is estimated to be about 12,000,000,000 years old.

Question 125:

Express the number appearing in the following statements in standard form.
The distance of the Sun the from the centre of the Milky Way Galaxy is estimated to be 300,000,000,000,000,000,000 m.

Question 126:

Express the number appearing in the following statements in standard form.
60,230,000,000,000,000,000,000 molecules are contained in a drop of water weighing 1.8 gm.

Question 127:

Express the number appearing in the following statements in standard form.
The earth has 1,353,000,000 cubic km of sea water.

Question 128:

Express the number appearing in the following statements in standard form.
The population of India was about 1,027,000,000 in March, 2001.