Question 1:
Can two acute angles be complement to each other?
Answer:
Yes, two acute angles are complementary to each other only if the sum of them is 90°.
Question 2:
Can two obutse angles be complement to each other?
Answer:
No, two obtuse angles cannot be complement of each other because their sum will be greater than 90°.
Question 3:
Can two right angles be complement to each others.
Answer:
No, two right angles can never be complement of each other, since their sum is also greater than 90°.
Question 4:
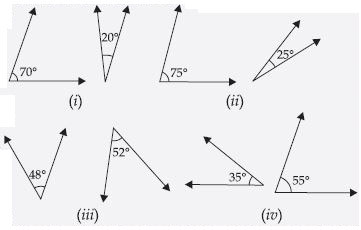
Which pairs of the following angles are complementary?
Answer:
Pairs (i) and (iv) are complementary.
Since in pair (i) 70° + 20° = 90° and in pair (iv) 35° + 55° = 90°
Question 5:
What is the measure of the complement of each of the following angles?
(i) 45°
(ii) 65°
(iii) 41°
(iv) 54°
Answer:
(i) Complement of 45° = 90° – 45° = 45°
(ii) Complement of 65° = 90° – 65° = 25°
(iii) Complement of 41° = 90° – 41° = 49°
(iv) Complement of 54° = 90° – 54° = 36°
Question 6:
The difference in the measures of two complementary angles is 12°. Find the measures of the angles.
Answer:
Let the given angle be = x°
Therefore its complement = 90° – x°
Their difference = 12°
∴ x° – (90° – x°) = 12°
or, x° – 90° + x° = 12°
or, x° + x° = 12° + 90°
or, 2x° = 102°
or, x° = 102/2 = 51°
∴ First angle = 51°
Other angle = 90° – 51° = 39°
∴ The required angles are 51° and 39°.
Question 7:
Can two obtuse angles be supplementary?
Answer:
No, two obtuse angles cannot be supplementary because the sum of two obtuse angles would be more than 180°.
Question 8:
Can two acute angles be supplementary?
Answer:
No, two acute angles cannot be supplementary because the sum of two angles would be less than 180°.
Question 9:
Can two right angles be supplementary?
Answer:
Yes, two right angles be supplementary because measure of each right angle is 90°.
∴ 90° + 90° = 180° = Supplementary
Question 10:
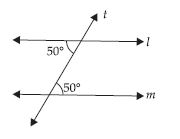
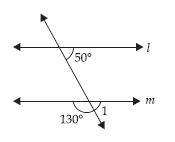
Find the pairs of supplementary angles in the following given fig.
Answer:
The angles shown in figure (iii) are supplementary because in figure (iii) 130° + 50° = 180°.
Question 11:
What will be the measure of supplement of the following angles?
(i) 100° (ii) 90°
(iii) 55° (iv) 125°
Answer:
We know that the sum of two supplementary angles is 180°,
Therefore,
(i) Supplement of 100° = 180° – 100° = 80°
(ii) Supplement of 90° = 180° – 90° = 90°
(iii) Supplement of 55° = 180° – 55° = 125°
(iv) Supplement of 125° = 180° – 125° = 55°
Question 12:
Among two supplementary angles the measure of the larger angle is 44° more than the measure of the smaller. Find their measures.
Answer:
Let the smaller angle be = x°
Therefore, its supplement bigger angle = (x + 44)°
Since the sum of two supplement angles is 180°
∴ x° + (x + 44)° = 180°
or 2x° = 180° – 44° = 136°
Therefore, the smaller angle = 68°
and its supplement larger angle = 68° + 44° = 112°
Question 13:
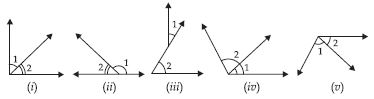
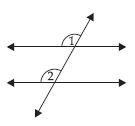
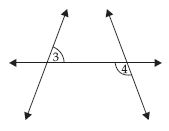
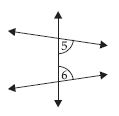
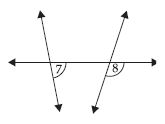
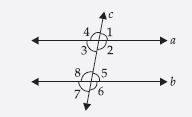
Are the angles marked 1 and 2 adjacent? If they are not adjacent, say, ‘why’.
Answer:
(i) In figure (i), angles 1 and 2 are adjacent angles because they have a common vertex and a common arm but no
common interior points.
(ii) Angles in the figure (ii) are also adjacent angles.
(iii) Angles in the figure (iii) are not adjacent angles.
Reason: In figure (iii), angles 1 and 2 do not fulfil the first condition i.e. they have no common vertex. So, these angles
are not adjacent angles.
(iv) Angles in the figure (iv) are not adjacent angles.
Reason: In figure (iv), angles 1 and 2 do not fulfil the condition that there are no common interior points.
(v) Angles in figure (v) are adjacent angles.
Question 14:
In the given figure which of the following are adjacent angles?
(a) AOB and BOC
(b) BOD and BOC
Answer:
(a) AOB and BOC are adjacent angles.
Reason: Because AOB and BOC have a common vertex O and a common arm OB. They do not have common interior
points.
(b) BOD and BOC are not adjacent angles.
Reason: BOD and BOC have a common vertex O and a common arm OB. But they do not fulfil the third
condition i.e. they have common interior point C.
Question 15:
Can two adjacent angles be supplementary?
Answer:
Yes, two adjacent angles can be supplementary if their sum is 180°.
Question 16:
Can two adjacent angles be complementary?
Answer:
Yes, two adjacent angles can be complementary if their sum is 90°.
Question 17:
Can two obtuse angles be adjacent angles?
Answer:
Yes, two obtuse angles can be adjacent.
Question 18:
Can an acute angle be adjacent to an obtuse angle?
Answer:
Yes, an acute angle can be adjacent to an obtuse angle.
Question 19:
Can two acute angles form a linear pair?
Answer:
No, two acute angles cannot form a linear pair.
Reason: The sum of two angles forming a linear pair is always 180°. But the
sum of two acute angles is always less than 180°.
Question 20:
Can two obtuse angles form a linear pair?
Answer:
No, two obtuse angles cannot form a linear pair.
Reason: The sum of two obtuse angle will be
greater than 180°.
Question 21:
Can two right angles form a linear pair?
Answer:
Yes, two right angles can form a linear pair, because the sum of two right angles is 180°.
Question 22:
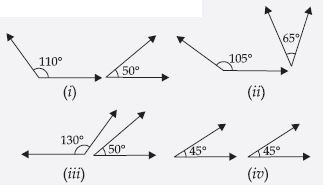
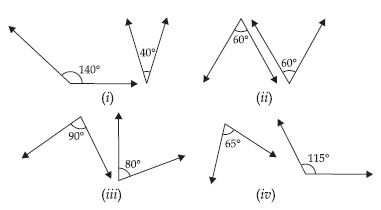
Check which of the following pairs of angles form a linear pair:
Answer:
Pairs (i) and (iv) will form a linear pair.
In fig. (i) 140° + 40° = 180°
In fig. (iv) 65° + 115° = 180°
Question 23:
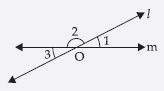
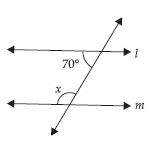
In the given figure, if 1 = 30°, find 2 and 3.
Answer:
Since 1 and 2 form a linear pair
∴ 1 + 2 = 180°
∴ 30° + 2 = 180°
or 2 = 180° – 30° = 150°
Now, 3 and 1 form a pair of vertically opposite
angles.
∴ 3 = 1
But 1 = 30°
∴ 3 = 30°
Question 24:
Give an example of vertically opposite angles in your surroundings.
Answer:
Arms of the table stand forms a pair of vertically opposite angles.
Question 25:
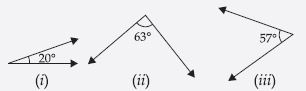
Find the complement of each of the following angles:
Answer:
We know that the sum of complementary angles is 90°. Therefore,
(i) Complement of 20° = 90° – 20° = 70°
(ii) Complement of 63° = 90° – 63° = 27°
(iii) Complement of 57° = 90° – 57° = 33°
Question 26:
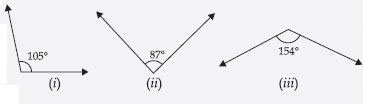
Find the supplement of each of the following angles:
Answer:
We know that the sum of supplmentary angles is 180°.
Therefore,
(i) Supplement of 105° = 180° – 105° = 75°
(ii) Supplement of 87° = 180° – 87° = 93°
(iii) Supplement of 154° = 180° – 154° = 26°
Question 27:
Identify which of the following pairs of angles are complementary and which are
supplementary.
(i) 65°, 115° (ii) 63°, 27°
(iii) 112°, 68° (iv) 130°, 50°
(v) 45°, 45° (vi) 80°, 10°.
Answer:
The pairs of angles in (ii), (v) and (vi) are complementary angles.
Because (ii) 63° + 27° = 90°, (v) 45° + 45° = 90°
and (vi) 80° + 10° = 90°
The pairs of angles in (i), (iii) and (iv) are supplementary angles.
Because (i) 65° + 115° = 180°, (ii) 112° + 68° =
180° and (iv) 130° + 50° = 180°.
Question 28:
Find the angle which is equal to its complement.
Answer:
Let the angle be = x°
Therefore its complement = 90° – x°
Since the angle is equal to its complement
∴ x° = 90° – x°
or x° + x° = 90°
or 2x° = 90°
or x° = 90°/2
or x° = 45°
Therefore the required angle is 45°.
Question 29:
Find the angle which is equal to its supplement.
Answer:
Let the angle be x°
Therefore its supplement = 180° – x°
Since the angle is equal to its supplement
∴ x° = 180° – x°
or x° + x° = 180°
or 2x° = 180°
or x° = 180°/2
= 90°
Therefore, the required angle is 90°.
Question 30:
In the given figure, 1 and 2 are supplementary angles. If 1 is decreased, what changes should take place in 2 so that both the angles still remain supplementary.
Answer:
If 1 is decreased, then 2 should be increased so that both the angles still remain supplementary.
Question 31:
Can two angles be supplemantary if both of them are:
(i) acute?
(ii) obtuse?
(iii) right?
Answer:
Since two angles be supplementary if sum of two angles is 180°.
(i) No; if two angles be acute (0° < q < 90°) then their sum cannot be equal to 180°.
(ii) No; if two angles be obtuse (90° < q < 180°) then their sum cannot be equal to
180°.
(iii) Yes; if two angles are right angle (= 90°) then their sum be 180°.
Question 32:
An angle is greater than 45°. Is its complementary angle greater than 45° or equal to 45° or less than 45°?
Answer:
Since the sum of two complementary angles is 90°.
So, if an angle is greater than 45°, then its complementary angle is less than 45°.
Question 33:
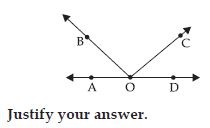
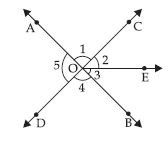
In the given figure,
(i) Is 1 adjacent to 2?
(ii) AOC adjacent to AOE?
(iii) Do COE and COD form a linear pair?
(iv) Are BOD and DOA supplementary?
(v) Is 1 vertically opposite to 4?
(vi) What is the vertically opposite angle of 5?
Answer:
(i) Yes, 1 is adjacent to 2.
(ii) No, AOC is not adjacent to AOE becuase they have common interior point C.
(iii) No, COE and COD do not form a linear pair.
(iv) Yes, BOD and DOA are supplementary because they form a straight angle i.e. 180°.
(v) Yes, 1 is vertically opposite to 4.
(vi) BOC is the vertically opposite angle of 5.
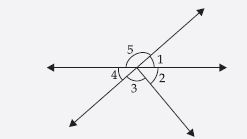
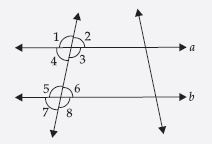
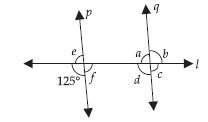
Question 34:
Indicate which pairs of angles are:
(i) Vertically opposite angles.
(ii) Linear pairs.
Answer:
(i) 1, 4 and 5, 2 + 3 are vertically opposite angles.
(ii) 1, 5 and 4, 5 form a linear pair.
Question 35:
In the given figure, is 1 adjacent to 2? Give reasons.
Answer:
No, 1 is not adjacent to 2.
Reason: 1 and 2 do not fullfil the first condition of adjacent angles i.e. they do not have a
common vertex.
Question 36:
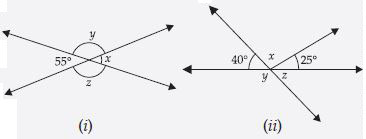
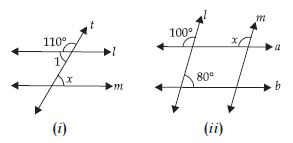
Find the values of the angles x, y and z in each of the following:
Answer:
In fig. (i) x = 55° (Vertically opposite angles)
y + 55° = 180° (Linear pair)
∴ y = 180° – 55° = 125°
y = z (Vertically Opposite angles)
= 125°
In fig. (ii) y + 40° = 180° (Linear pair)
∴ y = 180° – 40° = 140°
z = 40° (Vertically opposite angles)
x + 25° + 40° = 180° (Linear pair)
∴ x = 180° – 25° – 40°
= 115°
Question 37:
If two angles are complementary, then the sum of their measures is _______________.
Answer:
90°
Question 38:
If two angles are supplementary, then the sum of their measures is _______________.
Answer:
180°
Question 39:
Two angles forming a linear pair are _______________.
Answer:
adjacent angles and supplementary
Question 40:
If two adjacent angles are supplementary, they form a _______________.
Answer:
linear pair
Question 41:
If two lines intersect at a point, then the vertically opposite angles are always _______________.
Answer:
equal
Question 42:
If two lines intersect at a point, and if one pair of vertically opposite angles are acute angles, then the other pair of vertically opposite angles are _______________.
Answer:
obtuse angles
Question 43:
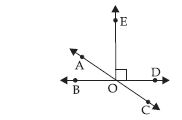
In the adjoining figure, name the following pairs of angles.
(i) Obtuse vertically opposite angles
(ii) Adjacent complementary angles
(iii) Equal supplementary angles
(iv) Unequal supplementary angles
(v) Adjacent angles that do not form a linear pair
Answer:
(i) A pair of obtuse vertically opposite angles are AOD and BOC.
(ii) Adjacent complementary angles are AOB and AOE.
(iii) Equal supplementary angles are BOE and EOD.
(iv) Unequal supplementary angles are EOA ; EOC
(v) Adjacent angles that do not form a linear pair are AOB, AOE; AOE, EOD; EOD, COD.
Question 44:
Find examples from your surroundings where lines intersect at right angles.
Answer:
Corners of the walls, sides of a box.
Question 45:
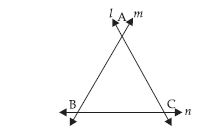
Find the measure of the angles made by the intersecting lines at the vertices of an equilateral triangle.
Answer:
Let us draw an equilateral triangle ABC with the help of three intersecting lines l, m and n intersecting each other at A, B and C respectively.
On measuring the angles at the vertices A, B and C respectively, we see that each angle is 60°.Question 46:
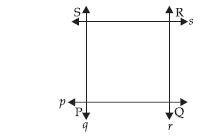
Draw any rectangle and find the measures of angles at the four vertices made by the intersecting lines.
Answer:
Let us draw a rectangle PQRS with the help of four lines p, q, r and s interesecting each other at P, Q, R and S respectively. On measuring angles at the vertices P, Q, R and S respectively. We see that angles at the vertices P, Q, R and S are right angles.
Question 47:
If two lines intersect, do they always intersect in right angles?
Answer:
No, they should always not intersect in right angles.
Question 48:
Suppose two lines are given. How many transversals can you draw for these lines?
Answer:
We can draw infinite number of transversals.
Question 49:
If a line is a transversal to three lines, how many points of interection are there?
Answer:
When a line is a transversal to three lines, then there are three points of intersection.
Question 50:
Give few examples of transversals in your surroundings.
Answer:
(i) A road crossing two or more roads.
(ii) A railway line crossing several other lines.
Question 51:
Name the pairs of angles in each figure.
Answer:
1 and 2 are pairs of corresponding angles.
Question 52:
Name the pairs of angles in each figure.
Answer:
3 and 4 are alternate interior angles.
Question 53:
Name the pairs of angles in each figure.
Answer:
5 and 6 are pairs of interior angles on the same side of the transversal.
Question 54:
Name the pairs of angles in each figure.
Answer:
7 and 8 are pairs of corresponding angles.
Question 55:
Name the pairs of angles in each figure.
Answer:
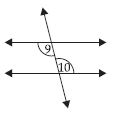
9 and 10 are alternate interior angles.
Question 56:
Name the pairs of angles in each figure.
Answer:
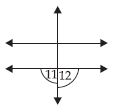
11 and 12 are exterior angles.
Question 57:
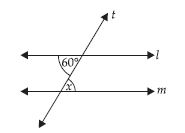
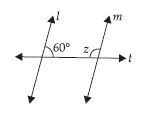
Lines l|| m; t is transversal x =?
Answer:
l || m and t is a transversal
∴ x = 60° (Alternate interior angles)
Question 58:
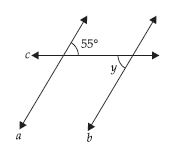
Lines a || b; c is transversal y =?
Answer:
a || b and c is a transvearsal.
∴ y = 55° (Alternate interior angles)
Question 59:
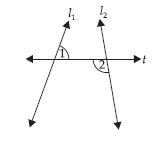
l1, l2 be two lines t is transversal. Is 1 = 2?
Answer:
l1 and l2 is not parallel and t is a transversal.
∴ 1 2
Question 60:
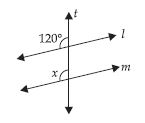
Lines l || m ; t is a transversal z =?
Answer:
lines l || m and t is a traversal
∴ z + 60° = 180° .... (Pairs of interior angles on the same side of the
transversal)
z = 180° – 60° = 120°
Question 61:
Lines l || m and t is a transversal x =?
Answer:
lines l || m and t is a traversal
∴ x = 120°
.... (Pairs of corresponding angles)
Question 62:
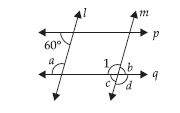
Lines l || m ; p || q; find a, b, c, d.
Answer:
p || q and l is a transversal
∴ a + 60° = 180°.... (Pairs of interior angles
on the same side of the transversal)
a = 180° – 60°
a = 120°
l || m and q is transversal
∴ a = 1 ....(Pairs of corresponding angles)
o r 1 = 120°
d = 1 = 120° .... (Vertically opposite
angles)
1 + c = 180° (Linear Pair)
120° + c = 180°
c = 180° – 120°
c = 60°
b = c .... (Vertically opposite angles)
b = 60°.
Question 63:
Is l || m? Why?
Answer:
Since alternate interior angles are equal.
∴ l || m
Question 64:
Is l || m? Why?
Answer:
Since corresponding angles are equal.
∴ 1 = 180° – 130° (linear pair)
1 = 50°
∴ l || m.
Question 65:
Is l || m? Why?
Answer:
l || m.
∵ The sum of the interior angles on the same side of the transversal is supplementary.
∴ x + 70° = 180°
∴ x = 180° – 70° = 110°
Question 66:
State the property that is used in each of the following statements?
(i) If a || b, then 1 = 5.
(ii) If 4 = 6, then a || b.
(iii) If 4 + 5 = 180°, then a || b.
Answer:
(i) a || b, then 1 = 5 If a transversal intersects two parallel lines then the corresponding angles are
equal.
∴ By corresponding angle property, it is true.
(ii) If 4 = 6, then a|| b. If a transversal intersects two parallel lines then the alternate
interior angles are equal.
∴ By alternate interior angle property it is true.
(iii) If a transversal intersects two parallel lines, then the interior angles on the same
side of the transversal are supplementary.
Question 67:
In the given figure, identify:
(i) The pairs of corresponding angles.
(ii) The pairs of alternate interior angles.
(iii) The pairs of interior angles on the same side of the transversal.
(iv) The vertically opposite angles.
Answer:
(i) Pairs of corresponding angles are:
1, 5 ; 2, 6 ; 3, 7 ; 4, 8
(ii) Pairs of alternate interior angles are:
2, 8 ; 3, 5
(iii) Pairs of interior angles on the same side of the transversal are:
2, 5 ; 3, 8
(iv) Vertically opposite angles are:
1, 3 ; 2, 4 ; 5, 7 ; 6, 8
Question 68:
In the adjoining figure, p || q, find the unknown angles.
Answer:
p || q and l is transversal
∴ e + 125° = 180° (Linear Pair)
e = 180° – 125°
e = 55°
f = e (vertically opposite angles)
f = 55° (∵ e = 55°)
a = e (Corresponding angles)
a = 55° (∵ e = 55°)
c = a (vertically opposite angles)
c = 55° (∵ a = 55°)
d = 125° (Corresponding angles)
b = d (vertically opposite angles)
b = 125° (∵ d = 125°)
Hence, a = 55°, b = 125°, c = 55°, d = 125°, e = 55°, f = 55°
Question 69:
Find the value of x in each of the following figures if l || m.
Answer:
(i) 1 + 110° = 180° (Linear Pair of angles)
1 = 180° – 110°
1 = 70°
But, x = 1 (alternate angles)
x = 70° (∵ 1 = 70°)
(ii) l || m and a is transversal
x = 100° (Corresponding angles)
Question 70:
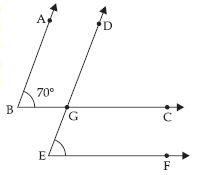
In the given figure, the arms of two angles are parallel. If ABC = 70°, then find:
(i) DGC
(ii) DEF.
Answer:
(i) AB || DE and BC is transversal
∴ DGC = ABC
(Corresponding angles)
But ABC = 70° (Given)
∴ DGC = 70°
(ii) BC || EF and DE is transversal
∴ DEF = DGC
(Corresponding angles)
But DGC = 70°
∴ DEF = 70°.
Question 71:
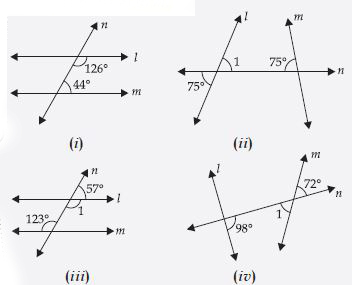
In the given fugures below, decide whether l is parallel to m.
Answer:
(i) l is not parallel to m.
Reason: Q 126° + 44° = 170° ; which is not equal to 180°.
(ii) l is not parallel to m
Reason: Q 1 = 75° (Vertically opposite angles) and 75° + 75° = 150° ; which is not equal to
180°.
(iii) l is parallel to m.
Reason: Q 1 + 57° = 180°
(Linear Pair angles)
1 = 180° – 57°
1 = 123°
But these are alternate angles.
(iv) l is not parallel to m.
Reason: 1 = 72° (Vertically opposite angles)
and 72° + 98° = 170°; which is not equal to 180°.