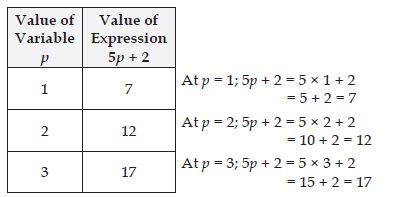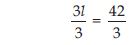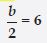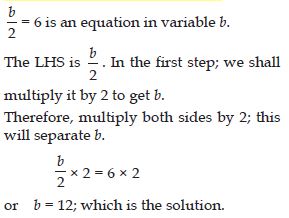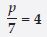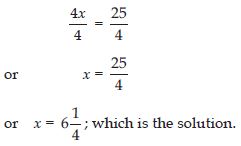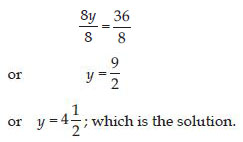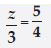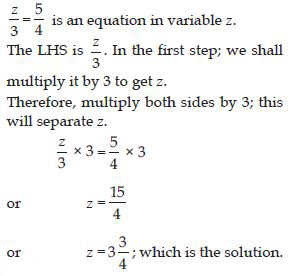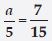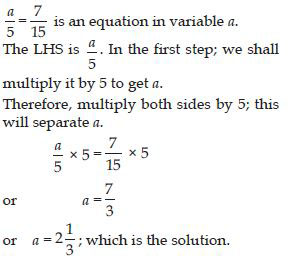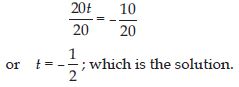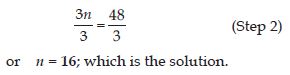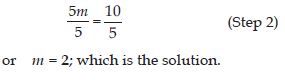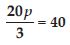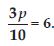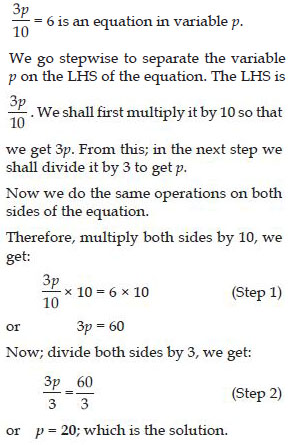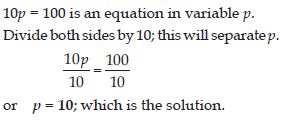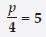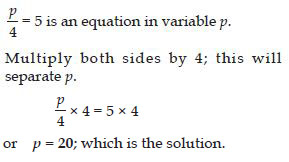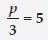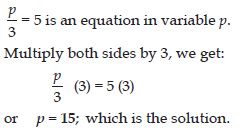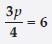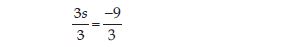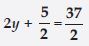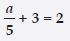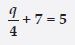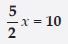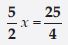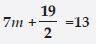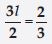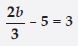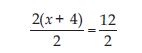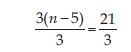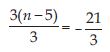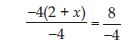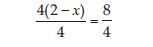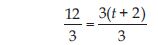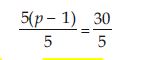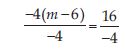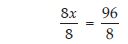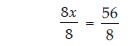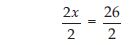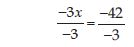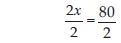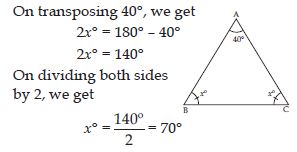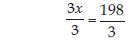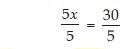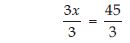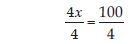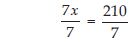Question 1:
The value of the expression (10y – 20) depends on the value of y. Verify this by giving five different values to y and finding the value of (10y – 20) for each. From the different values of (10y – 20) you obtain, do you see a solution to 10y – 20 = 50? If there is no solution, try giving more values to y and find whether the condition 10y – 20 = 50 is met.
Answer:
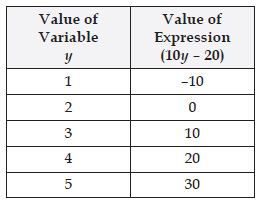
In the following we find the value of expression (10y – 20) by taking 5 different values of
y.
When y = 1; 10y – 20 = 10 × 1 – 20 = 10 – 20 = – 10
When y = 2; 10y – 20 = 10 × 2 – 20 = 20 – 20 = 0
When y = 3; 10y – 20 = 10 × 3 – 20 = 30 – 20 = 10
When y = 4; 10y – 20 = 10 × 4 – 20 = 40 – 20 = 20
When y = 5; 10y – 20 = 10 × 5 – 20 = 50 – 20 = 30
From the above table; We observe that for each value of variable y there corresponds to a
unique value of expression (10y – 20).
Thus, it is verified that the value of expression (10y – 20) depends on the value of y.
For 5 different values of y, we could not find the solution to the equation 10y – 20 =
50.
Let us try for more values to y.
When y = 6; 10y – 20 = 10 × 6 – 20 = 60 – 20 = 40
When y = 7; 10y – 20 = 10 × 7 – 20 = 70 – 20 = 50
Since equation 10y – 20 = 50 is satisfied at y = 7. Hence by trial and error method y = 7 is
the solution to the equation 10y – 20 = 50.
Question 2:
Write at least one other form for equation 5p = 20.
Answer:
Statement forms for equation 5p = 20 are as follows:
1. If you multiply a number p by 5; you get 20.
2. A number p multiplied by 5 gives 20.
Question 3:
Write at least one other form for equation 3n + 7 = 1.
Answer:
Statement forms for equation 3n + 7 = 1 are as follows:
1. The sum three times n and 7 is 1.
2. Three times a number n plus 7 gives 1.
3. If you add 7 to a number n multiplied by 3; you get 1.
Question 4:
Write at least one other form for equation m/5 – 2 = 6.
Answer:
Statement forms for equation m/5 – 2 = 6 are as follows:
1. If you subtract 23 from a number m divided by 5; you get 6.
2. One fifth of m is greater by 6 than 2.
3. The difference between one fifth of a number m and 2 is 6.
Question 5:
Complete the last column of the table.
Answer:
No.
Reason: For x = 3; x + 3 = 3 + 3 = 6
[Put x = 3; on the LHS of the equation x + 3 = 0]
But result on the RHS of the equation x + 3 = 0 is 0.
Since, 6 0.
Therefore, the given equation is not satisified for x = 3.
Question 6:
Complete the last column of the table.
Answer:
No.
Reason: For x = 0; x + 3 = 0 + 3 = 3
[Put x = 0; on the LHS of the equation x + 3 = 0]
But result on the RHS of the equation x + 3 = 0 is 0.
Since, 3 0.
i.e. LHS RHS
Therefore, equation is not satisfied for x = 0.
Question 7:
Complete the last column of the table.
Answer:
Yes.
Reason: For x = –3; x + 3 = – 3 + 3 = 0
[Put x = – 3; on the LHS of the equation x + 3 = 0]
Result on the RHS of the equation x + 3 = 0 is also 0.
Since, 0 = 0.
Therefore, given equation is satisfied for x = –3.
Question 8:
Complete the last column of the table.
Answer:
No.
Reason: For x = 7; x – 7 = 7 – 7 = 0
[Put x = 7; on the LHS of the equation x – 7 = 1]
But result on the RHS of the equation x – 7 = 0 is 1.
Since, 0 1.
i.e. LHS RHS
Therefore, the given equation is not satisfied for x = 7.
Question 9:
Complete the last column of the table.
Answer:
Yes.
Reason: For x = 8; x – 7 = 8 – 7 = 1
[Put x = 8; on the LHS of the equation x – 7 = 1]
Result on the RHS of the equation x – 7 = 1 is also 1.
Since, 1 = 1.
Therefore, the given equation is satisfied for x = 8.
Question 10:
Complete the last column of the table.
Answer:
No.
Reason: For x = 0; 5x = 5 × 0 = 0
[Put x = 0; on the LHS of the equation 5x = 25]
But result on the RHS of the equation 5x = 25 is 25.
Since, 0 25
Therefore, the given equation is not satisfied for x = 0.
Question 11:
Complete the last column of the table.
Answer:
Yes.
Reason: For x = 5; 5x = 5 × 5 = 25
[Put x = 5; on the LHS of the equation 5x = 25]
Result on the RHS of the equation is also 25.
Since, 25 = 25.
Therefore, the given equation is satisfied for x = 5.
Question 12:
Complete the last column of the table.
Answer:
No.
Reason: For x = –5; 5x = 5 × (–5) = –25
[Put x = –5; on the LHS of the equation 5x = 25]
But result on the RHS of the equation 5x = 25 is 25.
Since, –25 25.
i.e. LHS RHS
Therefore the given equation is not satisfied for x = –5.
Question 13:
Complete the last column of the table.
Answer:
No.
Reason: For m = –6; m/3 = − 6/3 = – 2
[Put m = –6; on the LHS of the equation m/3 = 2]
But result on the RHS of the equation m/3 = 2 is 2.
Since, –2 2.
Therefore, the given equation is not satisfied for m = –6.
Question 14:
Complete the last column of the table.
Answer:
No.
Reason: For m = 0; m/3 = 0/3 = 0
[Put m = 0; on the LHS of the equation m/3 = 2]
But result on the RHS of the equation m/3 = 2 is 2.
Since, 0 2.
Therefore, the given equation is not satisfied for m = 0.
Question 15:
Complete the last column of the table.
Answer:
Yes.
Reason: For m = 6; m/3 = 6/3 = 2
[Put m = 6; on the LHS of the equation m/3 = 2]
Result on the RHS of the equation m/3 = 2 is also 2.
Since, 2 = 2.
i.e. LHS = RHS
Therefore, the given equation is satisfied for m = 6.
Question 16:
Check whether the value given in the brackets is a solution to the given equation or not.
n + 5 = 19 (n = 1)Answer:
Equation n + 5 = 19 is a condition on variable n.
It states that the value of the expression n + 5 is 19.
When n = 1; n + 5 = 1 + 5 = 1 + 5 = 6
[Put n = 1 in LHS of equation 7n + 5 = 19]
Since, 12 6.
i.e. LHS RHS
It implies that equation n + 15 = 19 is not satisfied when n = 1.
Hence, n = 1 is not a solution to the given equation.
Question 17:
Check whether the value given in the brackets is a solution to the given equation or not.
7n + 5 = 19 (n = –2)
Answer:
Equation 7n + 5 = 19 is a condition on variable n.
It states that the value of the expression 7n + 5 is 19.
When n = –2; 7n + 5 = 7 (–2) + 5 = –14 + 5 = –9
[Put n = –2 in LHS of equation n + 5 = 19]
Since, –9 19
i.e. LHS RHS
It implies that equation 7n + 15 = 19 is not satisified when n = –2.
Hence, n = – 2 is not a solution to the given equation.
Question 18:
Check whether the value given in the brackets is a solution to the given equation or not.
7n + 5 = 19 (n = 2)Answer:
Equation 7n + 5 = 19 is a condition on variable n.
It states that the value of the expression 7n + 5 is 19.
When n = 2; 7n + 5 = 7 × 2 + 5 = 14 + 5 = 19
[Put n = 2 in LHS of equation 7n + 5 = 19]
Since, 19 = 19
It implies that the equation 7n + 15 = 19 is satisfied when n = 2.
Hence n = 2 is a solution to the given equation.
Question 19:
Check whether the value given in the brackets is a solution to the given equation or not.
4p – 3 = 13 (p = 1)
Answer:
Equation 4p – 3 = 13 is a condition on variable p.
It states that the value of the expression 4p – 3 is 13.
When p = 1; 4p – 3 = 4 × 1 – 3 = 4 – 3 = 1
[Put p = 1 in LHS of equation 4p – 3 = 13]
Since, 1 13.
i.e. LHS RHS
It implies that equation 4p + 3 = 13 is not satisfied when p = 1.
Hence, p = 1 is not a solution to the given equation.
Question 20:
Check whether the value given in the brackets is a solution to the given equation or not.
4p – 3 = 13 (p = – 4)
Answer:
Equation 4p – 3 = 13 is a condition on variable p.
It states that the value of the expression 4p – 3 is 13.
When p = –4; 4p – 3 = 4 (–4) – 3 = –16 – 3 = –19
[Put p = –4 in LHS of equation 4p – 3 = 13]
Since, –19 13.
i.e. LHS RHS
It implies that equation 4p + 3 = 13 is not satisfied when p = – 4.
Hence, and p = – 4 is not a solution to the given equation.
Question 21:
Check whether the value given in the brackets is a solution to the given equation or not.
4p – 3 = 13 (p = 0)
Answer:
Equation 4p – 3 = 13 is a condition on variable p.
It states that the value of the expression 4p – 3 is 13.
When p = 0; 4p – 3 = 4 × 0 – 3 = 0 – 3 = –3
[Put p = 0 in LHS of equation 4p – 3 = 13]
Since, –3 13.
It implies that equation 4p – 3 = 13 is not satisfied when p = 0.
Hence, and p = 0 is not a solution to the given equation.
Question 22:
Solve the following equations by trial and error method.
5p + 2 = 17
Answer:
To find the solution of equation 5p + 2 = 17 by trial and error method; we give different
values to variable p.
These values could be anything 1, 2, 3, 4, . . .
Then we find different values of expression 5p + 2 corresponding to the assumed different
values of variable p.
These are given in the following table as follows:
We observe that equation 5p + 2 = 17 is satisfied at p = 3.
Hence, p = 3 is a solution of the given equation.
Question 23:
Solve the following equations by trial and error method.
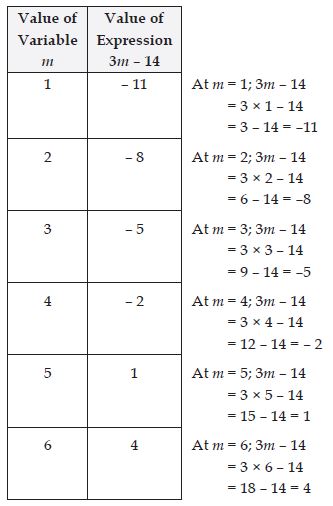
3m – 14 = 4
Answer:
To find the solution of equation 3m – 14 = 4 by trial and error method; we give different
values to variable m.
These values could be anything 1, 2, 3, 4, . . .
Then we find different values of expression 3m – 14 corresponding to the assumed different
values of variable m.
These are given in the following table as follows:
We observe that equation 3m – 14 = 4 is satisfied at m = 6.
Hence, m = 6 is a solution of the given equation.
Question 24:
Write equations for the following statement:
The sum of number x and 4 is 9.
Answer:
Sum of x and 4 is x + 4.
The sum is 9.
Therefore, the required equation is x + 4 = 9.
Question 25:
Write equations for the following statement:
2 subtracted from y is 8.
Answer:
Difference of y and 2 is y – 2.
The difference is 8.
Therefore, the required equation is y – 2 = 8.
Question 26:
Write equations for the following statement:
Ten times a is 70.
Answer:
Ten times a is 10a.
It is 70.
Therefore, the required equation is 10a = 70.
Question 27:
Write equations for the following statement:
The number b divided by 5 gives 6.
Answer:
The number b divided by 5 is b/5.
It is 6
Therefore, the required equation is b/5 = 6.
Question 28:
Write equations for the following statement:
Three fourth of t is 15.
Answer:
Three fourth of t is 3/4 t
It is 15
Therefore, the required equation is 3/4 t = 15.
Question 29:
Write equations for the following statement:
Seven times m plus 7 gets you 77.
Answer:
m plus 7 means we add 7 to m.
One gets m + 7
7 times m plus 7 is 7 (m + 7)
The result is 77.
Therefore; the required equation is 7 (m + 7) = 77.
Question 30:
Write equations for the following statement:
One fourth of a number minus 4 gives 4.
Answer:
Take a number to be n.
One fourth of n is n/4
One fourth of the number minus 4 is n/4 – 4
The result is 4.
Therefore; the required equation is n/4 – 4 = 4.
Question 31:
Write equations for the following statement:
If you take away 6 from 6 times y, you get 60.
Answer:
6 times y is 6y.
To take away 6 from 6 times y means subtracting 6 from 6y.
One gets 6y – 6
The result is 68.
Therefore, the required equation is 6y – 6 = 60.
Question 32:
Write equations for the following statement:
If you add 3 to one-third of z, you get 30.
Answer:
One third of z is n/4 z.
Addition of 3 to one third of z is
1/3 z + 3.
Therefore, the result is 30.
Therefore; the required equation is 1/3 z + 3 = 30.
Question 34:
Write the following equations in statement forms:
p + 4 = 15
Answer:
The sum of numbers p and 4 is 15.
Question 35:
Write the following equations in statement forms:
m – 7 = 3
Answer:
Taking away 7 from m gives 3.
Question 36:
Write the following equations in statement forms:
2m = 7
Answer:
Twice a number m is 7.
Question 37:
Write the following equations in statement forms:
m/5 = 3
Answer:
One-fifth of a number m is 3.
Question 38:
Write the following equations in statement forms:
3m/5 = 6
Answer:
Three fifth of a number m is 6.
Question 39:
Write the following equations in statement forms:
3p + 4 = 25
Answer:
Three times p when added to 4 gives you 25.
Question 40:
Write the following equations in statement forms:
4p – 2 = 18
Answer:
2 subtracted from four times a number p is 18.
Question 41:
Write the following equations in statement forms:
p/2 + 2 = 8
Answer:
Add 2 to half of a number p to get 8.
Question 42:
Set up an equation in the following case:
Irfan says that he has 7 marbles more than five times the marbles Parmit has. Irfan has 37
marbles. (Take m to be the number of Parmit’s marbles.)
Answer:
Take m to be the number of Parmit’s marble.
Five times m is 5m
7 more than five times m = 5m + 7
But 7 more than five times m = Number of Irfan’s marbles
Therefore, 5m + 7 = 37, which is an equation in variable m.
Question 43:
Set up an equation in the following case:
Laxmi’s father is 49 years old. He is 4 years older than three times Laxmi’s age. (Take
Laxmi’s age to be y years).
Answer:
Take y years to be the Laxmi’s age.
Three times Laxmi’s age = 3y
4 years older than three times Laxmi’s age = 3y + 4
But 4 years older than three times Laxmi’s age = age of Laxmi’s father
Therefore 3y + 4 = 49, which is an equation in variable y.
Question 44:
The teacher tells the class that the highest marks obtained by a student in her class is twice the lowest marks plus 7. The highest score is 87. (Take the lowest score to be l.)
Answer:
Take the lowest marks to be l.
Twice the lowest marks = 2l
Twice the lowest marks plus 7 = 2l + 7
But twice the lowest marks plus 7 = Highest marks obtained by a student.
Therefore, 2l + 7 = 87, which is an equation in variable l.
Question 45:
Set up an equation in the following case:
In an isosceles triangle, the vertex angle is twice either base angle. (Let the base angle
be b in degrees. Remember that the sum of angles of a triangle is 180 degrees.)
Answer:
In an isosceles triangle, let b be either base angle in degree.
Vertical angle = Twice the base angle = 2b
Sum of the angles of triangle = 180
Therefore, b + b + 2b = 180
or, 4b = 180, which is an equation in variable b.
Question 46:
Give first the step you will use to separate the variable and then solve the equation:
x – 1 = 0
Answer:
x – 1 = 0 is an equation in variable x.
The LHS is x – 1.
In the first step, we shall add 1 to it to get x.
Therefore, adding 1 to both sides of given equation, we get:
x – 1 + 1 = 0 + 1 (Step 1)
or, x = 1; which is the required solution.
Question 47:
Give first the step you will use to separate the variable and then solve the equation:
x + 1 = 0
Answer:
x + 1 = 0 is an equation in variable x.
The LHS is x + 1.
In the first step; we shall subtract 1 from it to get x.
Therefore, subtracting 1 from both sides of given equation, we get:
x + 1 – 1 = 0 – 1 (Step 1)
or, x = – 1; which is the required solution.
Question 48:
Give first the step you will use to separate the variable and then solve the equation:
x – 1 = 5
Answer:
x – 1 = 5 is an equation in variable x.
The LHS is x – 1.
In the first step; we shall add 1 to it to get x.
Therefore, adding 1 to both sides of given equation, we get:
x – 1 + 1 = 5 + 1 (Step 1)
or, x = 6; which is the required solution.
Question 49:
Give first the step you will use to separate the variable and then solve the equation:
x + 6 = 2
Answer:
x + 6 = 2 is an equation in variable x.
The LHS is x + 6.
In the first step; we shall subtract 6 from it to get x.
Therefore, subtracting 6 from both sides of given equation, we get:
x + 6 – 6 = 2 – 6 (Step 1)
or, x = –4; which is the solution.
Question 50:
Give first the step you will use to separate the variable and then solve the equation:
y – 4 = – 7
Answer:
y – 4 = – 7 is an equation in variable y.
The LHS is y – 4.
In the first step; we shall add 4 to it to get y.
Therefore, adding 4 to both sides of the given equation, we get:
y – 4 + 4 = – 7 + 4 (Step 1)
or, y = –3; which is the solution.
Question 51:
Give first the step you will use to separate the variable and then solve the equation:
y – 4 = 4
Answer:
y – 4 = 4 is an equation in variable.
The LHS is y – 4.
In the first step; we shall add 4 to it to get y.
Therefore, adding 4 to both sides of given equation, we get:
y – 4 + 4 = 4 + 4 (Step 1)
or, y = 8; which is the solution.
Question 52:
Give first the step you will use to separate the variable and then solve the equation:
y + 4 = 4
Answer:
y + 4 = 4 is an equation in variable y.
The LHS is y + 4.
In the first step; we shall subtract 4 from it to get y.
Therefore; subtracting 4 from both sides of given equation, we get:
y + 4 – 4 = 4 – 4 (Step 1)
or, y = 0; which is the solution.
Question 53:
Give first the step you will use to separate the variable and then solve the equation:
y + 4 = – 4
Answer:
y + 4 = –4 is an equation is variable y.
The LHS is y + 4.
In the first step; we shall subtract 4 from it to get y.
Therefore, subtracting 4 from both sides of given equation, we get:
y + 4 – 4 = – 4 – 4
or, y = –8; which is the solution.
Question 54:
Give first step you will use to separate the variable and then solve the equation:
3l = 42
Answer:
3l = 42 is an equation in variable l.
The LHS is 3l.
In the first step; we shall divide it by 3 to get l.
Therefore, divide both sides by 3; this will separate l.
or l = 14; which is the solution.
Question 55:
Give first step you will use to separate the variable and then solve the equation:
Answer:
Question 56:
Give first step you will use to separate the variable and then solve the equation:
Answer:
Question 57:
Give first step you will use to separate the variable and then solve the equation:
4x = 25
Answer:
4x = 25 is an equation in variable x.
The LHS is 4x. In first step; we divide it by 4 to get x.
Therefore, divide both sides by 4; this will separate x.
Question 58:
Give first step you will use to separate the variable and then solve the equation:
8y = 36
Answer:
8y = 36 is an equation in variable y.
The LHS is 8y. In the first step; we divide it by 8 to get y.
Therefore, divide both sides by 8; this will sepatate y.
Question 59:
Give first step you will use to separate the variable and then solve the equation:
Answer:
Question 60:
Give first step you will use to separate the variable and then solve the equation:
Answer:
Question 61:
Give first step you will use to separate the variable and then solve the equation:
20t = –10
Answer:
20t = –10 is an equation in variable t.
The LHS is 20t. In the first step; we divide it by 20 to get t.
Therefore, divide both sides by 20; this will separate t.
Question 62:
Give the steps you will use to separate the variable and then solve the equation:
3n – 2 = 46
Answer:
3n – 2 = 46 is an equation in variable n.
Add 2 to both sides, we get:
3n – 2 + 2 = 46 + 2 (Step 1)
or 3n = 48
Divide both sides by 3; this will separate n.
Question 63:
Give the steps you will use to separate the variable and then solve the equation:
5m + 7 = 17
Answer:
5m + 7 = 17 is an equation in variable m. We go stepwise to separate the variable m on the
LHS of the equation. The LHS is 5m + 7. We shall first subtract 7 from it so that we get 5m.
From this; in the next step we shall divide by 5 to get m.
Now we do the same operations on both sides of the equation.
Therefore; subtracting 7 from both sides, we get:
5m + 7 – 7 = 17 – 7 (Step 1)
or, 5m = 10
Now; divide both sides by 5, we get:
Question 64:
Give the steps you will use to separate the variable and then solve the equation:
Answer:
Question 65:
Give the steps you will use to separate the variable and then solve the equation:
Answer:
Question 66:
Solve the following equations:
10p = 100
Answer:
Question 67:
Solve the following equation:
10p + 10 = 100
Answer:
Question 68:
Solve the following equations:
Answer:
Question 69:
Solve the following equations:
Answer:
Question 70:
Solve the following equations:
Answer:
Question 71:
Solve the following equations:
3s = – 9
Answer:
3s = –9 is an equation in variable s. Divide both sides by 3; this will separate variable s.
or s = –3; which is the solution.
Question 72:
Solve the following equations:
3s + 12 = 0
Answer:
3s + 12 = 0 is an equation in variable s.
Subtract 12 from both sides, we get:
3s + 12 – 12 = 0 –12
or 3s = – 12
Divide both sides by 3 this will separate s.
or s = – 4; which is the solution.
Question 73:
Solve the following equations:
3s = 0
Answer:
3s = 0 is an equation in variable s.
Divide both sides by 3; this will separate s.
or s = 0; which is the solution.
Question 74:
Solve the following equations:
2q = 6
Answer:
2q = 6 is an equation in variable q.
Divide both sides by 2; this will separate q.
or q = 3; which is the solution.
Question 75:
Solve the following equations:
2q – 6 = 0
Answer:
2q – 6 = 0 is an equation in variable q.
Add 6 to both sides, we get:
2q – 6 + 6 = 0 + 6
or 2q = 6
Divide both sides by 2; this will separate q.
or q = 3; which is the solution.
Question 76:
Solve the following equations:
2q + 6 = 0
Answer:
2q + 6 = 0 is an equation in variable q.
Subtract 6 from both sides, we get:
2q + 6 – 6 = 0 – 6
or 2q = –6
Divide both sides by 2; this will separate q.
or q = –3; which is the solution.
Question 77:
Solve the following equations:
2q + 6 = 12
Answer:
2q + 6 = 12 is an equation in variable q.
Subtract 6 from both sides, we get:
2q + 6 – 6 = 12 – 6
or 2q = 6
Divide both sides by 2; this will separate q.
or q = 3; which is the solution.
Question 78:
Make two number puzzles, one with the solution 11 and another with 100.
Answer:
Let us follow the path to make a number puzzle in one variable with the solution 11.
Question 79:
Solve the following equation:
Answer:
Question 80:
Solve the following equation:
5t + 28 = 10
Answer:
Question 81:
Solve the following equation:
Answer:
Question 82:
Solve the following equation:
Answer:
Question 83:
Solve the following equation:
Answer:
Question 84:
Solve the following equation:
Answer:
Question 85:
Solve the following equation:
Answer:
Question 86:
Solve the following equation:
6z + 10 = – 2
Answer:
Question 87:
Solve the following equation:
Answer:
Question 88:
Solve the following equation:
Answer:
Question 89:
Solve the following equation:
2 (x + 4) = 12
Answer:
2(x + 4) = 12 is an equation in variable x. Divide both the sides by 2. This will remove the brackets in the LHS, we get:
or x = 6 – 4 (Transposing 4 to RHS)
or x = 2; which is the solution.
Check:
Putting x = 2; in the LHS of equation
2(x + 4) = 12.
LHS = 2 (x + 4)
= 2 (2 + 4)
= 2 × 6
= 12 = RHS as required.
Question 90:
Solve the following equation:
3 (n – 5) = 21
Answer:
3(n – 5) = 21 is an equation in variable n. Divide both the sides by 3. This will remove the brackets in the LHS, we get:
or n – 5 = 7
or n = 7 + 5 (Transposing – 5 to RHS)
or n = 12; which is the solution.
Check:
Putting n = 12; in the LHS of equation
3 (n – 5) = 21.
LHS = 3 (n – 5)
= 3 (12 – 5)
= 3 × 7
= 21 = RHS as required.
Question 91:
Solve the following equation:
3 (n – 5) = – 21
Answer:
3(n – 5) = – 21 is an equation in variable n.
Divide both the sides by 3. This will remove the brackets in the LHS, we get:
or n = –7 + 5 (Transposing – 5 to RHS)
or n = –2; which is the solution.
Check:
Putting n = –2; in the LHS of equation
3 (n – 5) = –21.
LHS = 3 (n – 5)
= 3 (–2 – 5)
= 3 (–7)
= –21 = RHS as required.
Question 92:
Solve the following equation:
– 4 (2 + x) = 8
Answer:
– 4 (2 + x) = 8 is an equation in variable x.
Dividing both sides by –4, we get:
or x = – 2 – 2 (Transposing 2 to RHS)
or x = –4; which is the solution.
Check:
Putting x = –4 in LHS of equation
–4 (2 + x) = 8
LHS = –4(2 – 4)
= –4 (–2)
= 8 = RHS as required.
Question 93:
Solve the following equation:
4 (2 – x) = 8
Answer:
4 (2 – x) = 8 is an equation in variable x.
Divide both the sides by 4. This will remove the bracket in the LHS; we get:
or 2 – x = 2
or – x = 2 – 2 (Transposing 2 to RHS)
or – x = 0
or x = 0; which is the solution.
Check:
Putting x = 0; in the LHS of the equation
4 (2 – x) = 8
LHS = 4(2 – 0)
= 4(2)
= 8 = RHS as required.
Question 94:
Solve the following equation:
4 = 5(p – 2)
Answer:
4 = 5(p – 2), is an equation in variable p
or 4 = 5p – 10
– 5p = – 10 – 4
[Transposing 5p to LHS and 4 to RHS]
or – 5p = – 14
Divide both the sides by – 5; this will separate variable p.
Question 95:
Solve the following equation:
– 4 = 5(p – 2)
Answer:
–4 = 5(p – 2), is an equation in variable p.
Divide both the sides by 5; this will remove the brackets in the RHS, we get:
Question 96:
Solve the following equation:
16 = 4 + 3(t + 2)
Answer:
16 = 4 + 3(t + 2) is an equation in variable t.
or 16 – 4 = 3(t + 2) (Transposing 4 to LHS)
or 12 = 3(t + 2)
Dividing both side by 3, we get:
or 2 = t
or t = 2; which is the solution.
Check:
Putting t = 2 ; in the RHS of the given equation.
RHS = 4 + 3(2 + 2)
= 4 + 3(4)
= 4 + 12
= 16 = LHS as required.
Question 97:
Solve the following equation:
4 + 5(p – 1) = 34
Answer:
4 + 5(p – 1) = 34 is an equation in variable p.
or 5(p – 1) = 34 – 4 (Transposing 4 to RHS)
or 5(p – 1) = 30
Dividing both side by 5, we get:
or p = 6 + 1 (Transposing 1 to RHS)
or p = 7; which is the solution.
Check:
Putting p = 7; in the LHS of the given equation.
LHS = 4 + 5(7 – 1)
or = 4 + 5(6)
or = 4 + 30
or = 34 RHS as required.
Question 98:
Solve the following equation:
0 = 16 + 4(m – 6)
Answer:
0 = 16 + 4 (m – 6) is an equation in variable m.
Transpose expression 4 (m – 6) to LHS, we get:
0 – 4 (m – 6) = 16
or – 4 (m – 6) = 16
Divide both the sides by – 4. This will remove the brackets on the LHS, we get:
or m – 6 = – 4
or m = – 4 + 6 (Transpose – 6 to RHS)
or m = 2; which is the solution.
Check:
Putting m = 2; in the RHS of given
equation,
RHS = 16 + 4 (2 – 6)
= 16 + 4 ( – 4)
= 16 – 16
= 0 = LHS as required.
Question 99:
Construct 3 equations starting with x = 2
Answer:
To build up the first equation;
Start with x = 2
Multiply both 3x = 6
sides by 3;
Add 7 to both sides, 3x + 7 = 13
This has resulted in an equation.
To build up the second equation;
Start with x = 2
Subtract 3 from both
the sides, x – 3 = – 1
Multiply both the sides
by 4, 4 (x – 3) = – 4
Add 11 to both the 4 (x – 3) + 11 = 7
sides,
This has resulted in an equation.
To build up the third equation;
Start with x = 2
Multiply both
the sides by –1, x (– 1) = 2 (– 1)
– x = – 2
Add 9 to both sides, – x + 9 = – 2 + 9
or 9 – x = 7
This has resulted in equation.
Question 100:
Construct 3 equations starting with x = – 2
Answer:
To build up the first equation;
Start with x = –2
Add 8 to the both
sides, x + 8 = 6
Multiply both the
sides by 5, 5 (x + 8) = 30
This has resulted in an equation.
To build up the second equation;
Start with x = – 2
Subtract 6
from the both sides, x – 6 = – 2 – 6
or x – 6 = – 8
Divide both ½(x – 6) = –4
the sides by 2,
This has resulted in an equation.
To build up the third equation;
Start with x = – 2
Multiply both 9x = – 18
sides by 9,
Divide both 9/2 x = – 9
sides by 2,
Add 5 to both 9/2 x + 5 = – 4
the sides,
This has resulted in an equation.
Question 101:
When you multiply a number by 6 and subtract 5 from the product, you get 7. Can you tell what the number is?
Answer:
Let, required number be x
Multiplying number with 6, we get 6x
By subtracting 5 from the product, we get 7
So, equation becomes
6x – 5 = 7 ... (1)
On transposing 5, we get
6x = 7 + 5
or 6x = 12
On dividing by 6, we get
or x = 12/6 = 2
Required number be 2.
Check:
Put x = 2 in LHS of (1), we get
LHS = 6 (2) – 5
= 12 – 5 = 7
= RHS
Hence, x = 2 is verified.
Question 102:
What is that number one third of which added to 5 gives 8?
Answer:
Let required number be x
One third of number added to 5 gives 8
So, equation becomes
x/3 + 5 = 8 ... (1)
On transposing 5, we get
x/3 = 8 – 5
or x/3 = 3
Multiplying by 3, we get
or x/3 × 3 = 3 × 3
or x = 9
Required number be 9.
Check:
Put x = 9 in LHS of (1), we get
LHS = 9/3 + 5
= 3 + 5 = 8
= RHS
Hence, x = 9 is verified.
Question 103:
There are two types of boxes containing mangoes. Each box of the larger type contains 4 more mangoes than the number of mangoes contained in 8 boxes of the smaller type. Each larger box contains 100 mangoes. Find the number of mangoes contained in the smaller box?
Answer:
Let, number of mangoes is smaller type box be x Number of mangoes in larger type box are 4
more than the number of mangoes contained in 8 boxes of the smaller type. So, equation
becomes
8x + 4 = 100 ... (1)
On transposing 4, we get
8x = 100 – 4
or 8x = 96
Dividing both sides by 8, we get
Hence, required number of mangoes in smaller box are 12.
Check:
Put x = 12 in LHS of (1), we get
LHS = 8 (12) + 4
= 96 + 4
= 100 = RHS
Hence, x = 12 is verified.
Question 104:
Set up equations and solve them to find the unknown numbers in the following case:
Add 4 to eight times a number; you get 60.
Answer:
Let required number be x.
Add 4 to eight times the number, we get 60.
8x + 4 = 60 ... (1)
On transposing 4, we get
8x = 60 – 4
8x = 56
On dividing both sides by 8, we get
or x = 7
Hence, required number be 7.
Check:
Put x = 7 is LHS of (1), we get
LHS = 8 (7) + 4
= 56 + 4
= 60 = RHS
Hence, x = 7 is verified.
Question 105:
Set up equations and solve them to find the unknown numbers in the following case:
One-fifth of a number minus 4 gives 3.
Answer:
Let required number be x.
One-fifth of the number minus 4 gives 3,
So, equation becomes
Question 106:
Set up equations and solve them to find the unknown numbers in the following case:
If I take three-fourths of a number and add 3 to it, I get 21.
Answer:
Let required number be x.
On taking three-fourth of the number and
count up 3 more, we get 21.
So, equation becomes
Question 107:
Set up equations and solve them to find the unknown numbers in the following case:
When I subtracted 11 from twice a number, the result was 15.
Answer:
Let required number be x.
On subtracting 11 from twice the number,
we get 15
So, equation becomes
2x – 11 = 15 ... (1)
On transposing 11, we get
2x = 15 + 11
or 2x = 26
On dividing both sides by 2, we get
Hence, required number be 13.
Check:
Put x = 13 in LHS of (1), we get
LHS = 2 (13) – 11
= 26 – 11
= 15 = RHS
Hence, x = 13 is verified.
Question 108:
Set up equations and solve them to find the unknown numbers in the following case:
When I subtracted 11 from twice a number, the result was 15.
Answer:
Let required number be x.
On subtracting 11 from twice the number,
we get 15
So, equation becomes
2x – 11 = 15 ... (1)
On transposing 11, we get
2x = 15 + 11
or 2x = 26
On dividing both sides by 2, we get
or x = 13
Hence, required number be 13.
Check:
Put x = 13 in LHS of (1), we get
LHS = 2 (13) – 11
= 26 – 11
= 15 = RHS
Hence, x = 13 is verified.
Question 109:
Set up equations and solve them to find the unknown numbers in the following case:
Munna subtracts thrice the number of notebooks he has from 50, he finds the result to be 8.
Answer:
Let number of note books Munna has x.
On subtracting thrice the number of note
books from 50, he gets 8.
So, equation becomes
50 – 3x = 8 ... (1)
On transposing 50, we get
– 3x = 8 – 50
or – 3x = – 42
On dividing both sides by – 3, we get
or x = 14
Hence, required number of note books are 14.
Check:
Put x = 14 in LHS of (1), we get
LHS = 50 – 3 (14)
= 50 – 42
= 8 = RHS
Hence, x = 14 is verified.
Question 110:
Set up equations and solve them to find the unknown numbers in the following case:
Ibenhal thinks of a number. If she adds 19 to it and divides the sum by 5, she will get 8.
Answer:
Let required number be x.
If we add 19 to it and divide the sum by 5, we get 8
So, equation becomes
Question 111:
Set up equations and solve them to find the unknown numbers in the following case:
Anwar thinks a number. If he takes away
7 from 5/2 of the number, the result is 23.
Answer:
Question 112:
Solve the following:
The teacher tells the class that highest marks obtained by a student in her class is twice
the lowest marks plus 7. The highest score is 87. What is the lowest score?
Answer:
Let the lowest marks in the class be x.
If we twice the lowest marks plus 7 we score 87 marks
So, equation becomes
2x + 7 = 87 ... (1)
On transposing 7, we get
2x = 87 – 7
2x = 80
Dividing both sides by 2, we get
or x = 40
Hence, lowest marks in the class is 40.
Check:
Put x = 40 in LHS of (1), we get
LHS = 2 (40) + 7
= 80 + 7
= 87 = RHS
Hence, x = 40 is verified.
Question 113:
Solve the following:
In an isosceles triangle, the base angles are equal. The vertex angle is 40. What are the base angles of the triangle? (Remember, the sum of three angles of a
triangle is 180)
Answer:
Let ABC be an isosceles triangle whose base angles are equal and of measure x.
Also, vertex angle is 40.
Since, sum of three angles of a triangle is 180.
A + B + C = 180
or 40 + x + x = 180
or 40 + 2x = 180 ... (1)
Hence, base angles are of measure 70.
Check:
Put x = 70 in LHS of (1), we get
LHS = 40 + 2 (70)
= 40 + 140
= 180 = RHS
Hence, x = 70 is verified.
Question 114:
Solve the following:
Sachin scored twice as many runs as Rahul. Together, their runs fell two short of a double
century. How many runs did each one score?
Answer:
Let runs scored by Rahul be x and runs scored by Sachin be 2x.
Since, the sum of their runs be two short of a double century.
So, equation becomes
x + 2x + 2 = 200
3x + 2 = 200 ... (1)
On trasnsposing 2, we get
3x = 200 – 2
or 3x = 198
Dividing both sides by 3, we get
or x = 66
Hence, runs scored by Rahul be 66 and by Sachin be 132.
Check:
Put x = 66 in LHS of (1), we get
LHS = 3 (66) + 2
= 198 + 2
= 200 = RHS
Hence, x = 66 is verified.
Question 115:
Solve the following:
Irfan says that he has 7 marbles more than five times the marbles Parmit has. Irfan has 37
marbles. How many marbles does Parmit have?
Answer:
Let, number of marbles Parmit has x.
If five times number of marbles of Parmit is added to 7, we get 37 marbles.
So, equation becomes
5x + 7 = 37 ... (1)
On transposing 7, we get
5x = 37 – 7
or 5x = 30
On dividing both sides by 5, we get
or x = 6
Hence, 6 marbles have Parmit.
Check:
Put x = 6 in LHS of (1), we get
LHS = 5 (6) + 7
= 30 + 7
= 37 = RHS
Hence, x = 6 is verified.
Question 116:
Solve the following:
Laxmi’s father is 49 years old. He is 4 years older than three times Laxmi’s age.
What is Laxmi’s age?
Answer:
Let Laxmi’s age be x years.
Laxmi’s father is 49 years old is 4 years older than three times Laxmi’s age.
So, equation becomes
3x + 4 = 49 ... (1)
On transposing 4, we get
3x = 49 – 4
3x = 45
On dividing both sides by 3, we get
or x = 15
Hence, Laxmi’s age be 15 years.
Check:
Put x = 15 in LHS of (1), we get
LHS = 3 (15) + 4
= 45 + 4
= 49 = RHS
Hence, x = 15 is verified.
Question 117:
Solve the following:
People of Sundargram planted trees in the village garden. Some of the trees were fruit
trees. The number of nonfruit trees were two more than three times the number of fruit
trees. What was the number of fruit trees planted if the number of non-fruit trees planted
was 77?
Answer:
Let number of fruit trees planted be x.
Sum of fruit trees and three times the number of fruit trees are two less from 102.
So, equation becomes
x + (3x + 2) = 102
4x + 2 = 102 ... (1)
On transposing 2, we get
4x = 102 – 2
or 4x = 100
On dividing both sides by 4, we get
Hence, number of fruit trees are 25.
Check:
Put x = 25 in LHS of (1), we get
LHS = 4 (25) + 2
= 100 + 2
= 102 = RHS
Hence, x = 25 is verified.
Question 118:
Solve the following riddle:
I am a number,
Tell my identity !
Take me seven times over
And add a fifty !
To reach a triple century
You still need forty !
Answer:
Let required number be x.
(i) Seven time of this number be 7x
(ii) Then add a fifity to it so it becomes
7x + 50
(iii) To reach a triple century, we need forty,
So, equation becomes
7x + 50 + 40 = 300
7x + 90 = 300 ... (1)
On transposing 90, we get
7x = 300 – 90
or 7x = 210
On dividing both sides by 7, we get
or x = 30
Hence, required number be 30.
Check:
Put x = 30 in LHS of (1), we get
LHS = 7 (30) + 90 = 210 + 90 = 300
= RHS
Hence, x = 30 is verified.