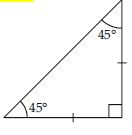
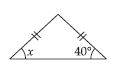
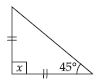
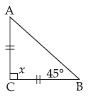
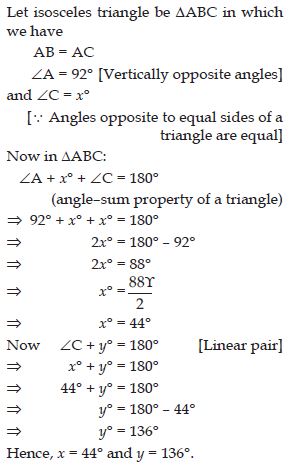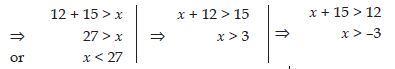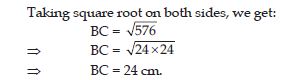Question 1:
Write the six elements (i.e. the 3 sides and 3 angles) of ABC.
Answer:
Six elements i.e. three sides and three angles of RBC are as follows :
Question 2:
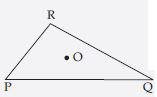
Write the side opposite to the vertex Q of PQR.
Answer:
Side opposite to the vertex Q of PQR is PR.
Question 3:
Write the angle opposite to the side LM of LMN.
Answer:
Angle opposite to side LM of LMN is MNL.
Question 4:
Write the vertex opposite to the side RT of RST.
Answer:
Vertex opposite to the side RT of RST is S.
Question 5:
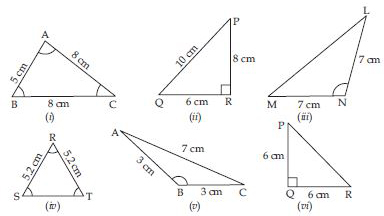
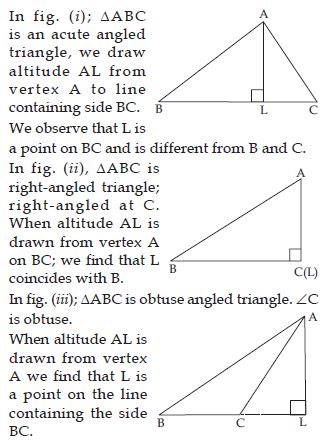
Look at the Fig. (i) to (vi) and classify each of the triangles according to its
(a) Sides (b) Angles.
Answer:
(i) ABC has two equal sides AC and BC each of length 8 cm, also each angle is acute.
Hence, ABC is an isosceles acute angled triangle.
(ii) In PQR, no two sides equal in length also QRP = 90.
Hence, PQR is a right-angled scalene triangle.
(iii) LMN has two equal sides; MN and LN each of length 7 cm, also each angle is acute.
Hence, LMN is an isosceles acute angled triangle.
(iv) RST has all three equal sides; RS, ST and RT each of length 5.2 cm.
Hence, RST is an equilateral triangle.
(v) ABC has two equal sides, AB and BC each of length 3 cm. Also ABC is obtuse.
Hence, ABC is an isosceles obtuse angled triangle.
(vi) PQR has two equal sides PQ and QR each of length 6 cm. Also PQR = 90
Hence, PQR is an isosceles right-angled triangle.
Question 6:
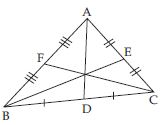
How many medians can a triangle have?
Answer:
Since there are three vertices and three sides of a triangle therefore a triangle has three medians. In the adjoining fig., D, E and F are the midpoints of line segments BC, AC and AB respectively. Therefore line segments; AD, BE and CF are three medians of ABC.
Question 7:
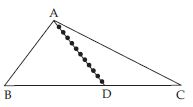
Does a median lie wholly in the interior of the triangle? (If you think that this is not true, draw a figure to show such a case).
Answer:
Median does not lie wholly in the interior of the triangle. It lies in the triangular
region.
Reason: In the adjoining fig., line segment AD is the median from A to D
(the midpoint of BC) The locus (family) of all points on AD (excluding A and D) lie in the
interior of ABC but points A and D lie on the boundary of ABC. Collectively we can say that median AD of triangle lie in the triangular region.
Question 8:
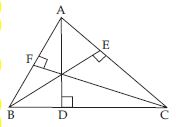
How many altitudes can a triangle have?
Answer:
Since there are three vertices and three sides of a triangle. Therefore a triangle has three
altitudes.
In the adjoining fig., AD BC, BE AC
and CF AB. Therefore line segments; AD, BE and CF are three altitudes.
Question 9:
Answer:
Question 10:
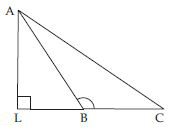
Will an altitude always lie in the interior of a triangle? If you think that this need not be true, draw a rough sketch to show such a case.
Answer:
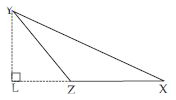
No; altitude always do not lie in the interior of a triangle. Reason: In the adjoining fig., ABC is an obtuse angled triangle; obtuse angled at B. The altitude AL drawn from A on produced CB lies in the exterior of triangle.
Question 11:
Can you think of a triangle in which two altitudes of the triangle are two of its sides?
Answer:
Yes, in right triangle altitudes of the triangle are two of its sides.
Question 11:
Can the altitude and median be same for a triangle?
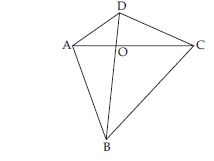
Answer:
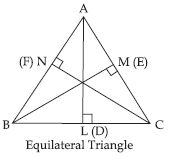
Yes, the altitude and median can be same only for equilateral triangle.
In an equilateral triangle; say ABC median AD and
altitude AL drawn from vertex A to the opposite side always coincide.
Similarly, altitude BM and median BE coincide.
Also, altitude CN and median CF coincides.
Question 12:
Answer:
Question 13:
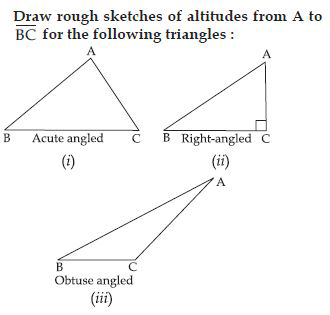
Draw rough sketches for the following:
In ABC, BE is a median.
Answer:
In the adjoining fig., we have ABC; in which line segment BE is the median drawn from B to AC.
Question 14:
Draw rough sketches for the following:
In PQR, PQ and PR are altitudes of the triangle.
Answer:
In the adjoining fig., we have PQR; in which PQ and PR are the altitudes drawn from Q to PR and from R to PQ respectively. In such case we have only right-angled triangle PQR right-angled at P.
Question 15:
Draw rough sketches for the following:
In XYZ, YL is an altitude in the exterior of the triangle.
Answer:
In the adjoining fig., we have an obtuse angled triangle XYZ in which YL is an altitude drawn
from Y to produced XZ.
Such altitude lies in the exterior of the triangle.
Question 16:
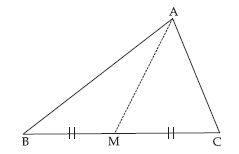
Verify by drawing a diagram if the median and altitude of an isosceles triangle can be same.
Answer:
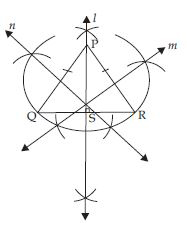
In the adjoining fig., we have an isosceles triangle
PQR such that PQ = PR when we draw perpendicular
bisectors l, m and n of sides QR, PR and PQ respectively.
We find that out of three perpendicular bisectors only l passes through the vertex P; common
to the equal sides PQ and PR.
Hence, only PS acts as median and altitude from
P to QR.
We conclude that in an isosceles triangle median and altitude drawn from the vertex (common
to the equal sides) to the third side are always same.
Question 17:
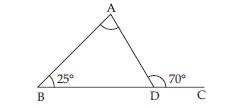
An exterior angle of a triangle is of measure 70 and one of its interior opposite angles is of measure 25, find the measure of the other interior opposite angle.
Answer:
Let ABC is the required triangle whose exterior
angle is of measure 70.
By Exterior angle property
A + B = ACD
or A + 25 = 70
B = 25 ...(Given)
ACD = 70 ...(Given)
or A = 70 – 25
or A = 45
Now, since sum of three angles of a triangle is of measure 180.
A + B + C = 180
45 + 25 + C = 180
C = 180 – 70
C = 110
Hence, A = 45 and C = 110.
Question 18:
The two interior opposite angles of an exterior angle of a triangle are 60 and 80, find the measure of the exterior angle.
Answer:
The two interior opposite angles are of measure 60 and 80.
By Exterior angle property,
Exterior angle = Sum of interior opposite angles
= 60 + 80 = 140
Question 19:
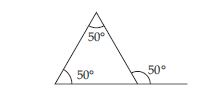
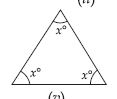
Comment on this diagram:
Answer:
As we know that:
Exterior angle = Sum of opposite interior angles
Therefore exterior angle = 50 + 50 = 100
Hence, in the diagram; exterior angle of measure 50 is irrelevant.
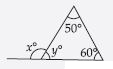
Question 20:
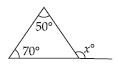
Find the value of the unknown exterior angle x in the following diagram:
Answer:
Exterior angle = Sum of interior opp. angles
x = 50 + 70
x = 120
x = 120
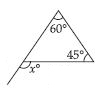
Question 21:
Find the value of the unknown exterior angle x in the following diagram:
Answer:
Exterior angle = Sum of interior opp. angles
x = 45 + 65
x = 110
x = 110
Question 22:
Find the value of the unknown exterior angle x in the following diagram:
Answer:
Exterior angle = Sum of interior opp. angles
x = 30 + 40
x = 70
x = 70
Question 23:
Find the value of the unknown exterior angle x in the following diagram:
Answer:
Exterior angle = Sum of interior opp. angles
x = 60 + 60
x = 120
x = 120
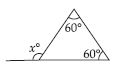
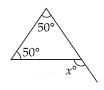
Question 24:
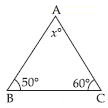
Find the value of the unknown exterior angle x in the following diagram:
Answer:
Exterior angle = Sum of interior opp. angles
x = 50 + 50
x = 100
x = 100
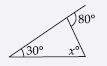
Question 25:
Find the value of the unknown exterior angle x in the following diagram:
Answer:
Exterior angle = Sum of interior opp. angles
x = 30 + 60
x = 90
x = 90
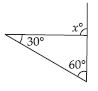
Question 26:
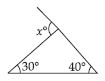
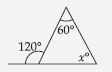
Find the value of the unknown interior angle x in the following diagram:
Answer:
Sum of interior opp. angles = Exterior angle
x + 50 = 115
x = 115 – 50
x = 65
x = 65
Question 27:
Find the value of the unknown interior angle x in the following diagram:
Answer:
Sum of Interior opp. angles = Exterior angle
x + 70 = 100
x = 100 – 70
x = 30
x = 30
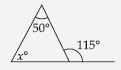
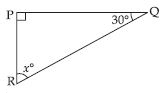
Question 28:
Find the value of the unknown interior angle x in the following diagram:
Answer:
Sum of interior opp. angles = Exterior angle
x + 90 = 125
x = 125 – 90
x = 35
x = 35
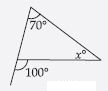
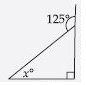
Question 29:
Find the value of the unknown interior angle x in the following diagram:
Answer:
Sum of interior opp. angles = Exterior angle
x + 60 = 120
x = 120 – 60
x = 60
x = 60
Question 30:
Find the value of the unknown interior angle x in the following diagram:
Answer:
Sum of interior opp. angles = Exterior angle
x + 30 = 80
x = 80 – 30
x = 50
x = 50
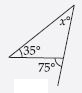
Question 31:
Find the value of the unknown interior angle x in the following diagram:
Answer:
Sum of Interior opp. angles = Exterior angle
x + 35 = 75
x = 75 – 35
x = 40
x = 40
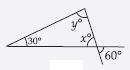
Question 32:
Find the value of unknown x in the following diagram:
Answer:
By angle-sum property of a triangle
In ABC,
x + 50 + 60 = 180
x = 180 – 50 – 60
= 180 – 110
x = 70
Hence, x = 70
Question 33:
Find the value of unknown x in the following diagram:
Answer:
In PQR,
x + 30 + 90 = 180
(By angle–sum property of a triangle)
x = 180 – 30 – 90
= 180 – 120
x = 60
Hence, x = 60
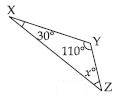
Question 34:
Find the value of unknown x in the following diagram:
Answer:
In XYZ,
x + 30 + 110 = 180
(By angle–sum property of a triangle)
x = 180 – 30 – 110
= 180 – 140
x = 40
Hence, x = 40
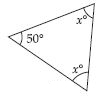
Question 35:
Find the value of unknown x in the following diagram:
Answer:
In the given isosceles triangle:
x + x + 50 = 180
(By angle–sum property of a triangle)
2x = 180 – 50
2x = 130
x = 130/2
x = 65
Hence, x = 65
Question 36:
Find the value of unknown x in the following diagram:
Answer:
In the given equilateral triangle:
x + x + x = 180
(By angle–sum property of a triangle)
3x = 180
x = 180/3
x = 60
Hence, x = 60
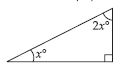
Question 37:
Find the value of unknown x in the following diagram:
Answer:
In the given right angled triangle:
x + 2x + 90 = 180
(By angle–sum property of a triangle)
3x = 180 – 90
3x = 90
x = 90/3
x = 30
Hence, x = 30
Question 38:
Find the values of the unknowns x and y in the following diagram:
Answer:
As we know that in a triangle;
Sum of interior opposite angles = Exterior angle
x + 50 = 120
x = 120 – 50
x = 70
Now in given triangle;
x + y + 50 = 180
(By angle-sum property of a triangle)
70 + y + 50 = 180
(putting x = 70 as found above)
y = 180 – 50 – 70
y = 180 – 120
y = 60
Hence, x = 70, y = 60.
Question 39:
Find the values of the unknowns x and y in the following diagram:
Answer:
y = 80 (vertically opposite angles)
y = 80
Now in the given triangle:
x + y + 50 = 180
(By angle-sum property of a triangle)
x + 80 + 50 = 180
(putting y = 80 as found above)
x = 180 – 80 – 50
x = 180 – 130
x = 50
Hence, x = 50, y = 80.
Question 40:
Find the values of the unknowns x and y in the following diagram:
Answer:
As we know that in a triangle
Exterior angle = Sum of interior opposite angles
x = 50 + 60
x = 110
Now in given triangle:
y + 50 + 60 = 180
(By angle-sum property of a triangle)
y = 180 – 50 – 60
y = 180 – 110
y = 70
Hence, x = 110, y = 70.
Question 41:
Find the values of the unknowns x and y in the following diagram:
Answer:
x = 60 [Vertically opposite angles]
x = 60
Now in given triangle:
x + y + 30 = 180
[By angle-sum property of a triangle]
60 + y + 30 = 180
[putting x = 60 as found above]
y = 180 – 60 – 30
y = 180 – 90
y = 90
Hence, x = 60, y = 90.
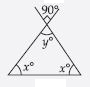
Question 42:
Find the values of the unknowns x and y in the following diagram:
Answer:
y = 90 (Vertically opposite angles)
y = 90
Now in given triangle:
x + x + y = 180
[By angle-sum property of a triangle]
2x + 90 = 180
[Putting y = 90 as found above]
2x = 180 – 90
2x = 90
x = 90/2
x = 45
Hence, x = 45, y = 90.
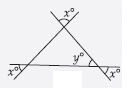
Question 43:
Find the values of the unknowns x and y in the following diagram:
Answer:
In each case:
y = x
(Vertically opposite angles)
Now in given triangle:
y + y + y = 180
[By angle-sum property of a triangle]
3y = 180
y = 180/3 = 60
Hence, x = 60; y = 60.
Question 43:
Two angles of a triangle are 30 and 80. Find the third angle.
Answer:
Let third angle be x
x + 30 + 80 = 180
[By angle-sum property of a triangle]
x = 180 – 30 – 80
x = 180– 110
x = 70
Hence, (x = 70)
Question 44:
One of the angles of a triangle is 80 and the other two angles are equal. Find the measure of each of the equal angles.
Answer:
Let each of the two equal angles be x. Therefore by angle-sum property of a triangle:
Question 45:
The three angles of a triangle are in the ratio 1 : 2 : 1. Find all the angles of the triangle. Classify the triangle in two different ways.
Answer:
Let three angles of a triangle be x, 2x and x.
Therefore,
x + 2x + x = 180
[By angle-sum property of a triangle]
4x = 180
x = 180/4
x = 45
Now three angles of given triangle are: x = 45,
2x = 2 × 45 = 90
and x = 45.
We observe that one angle is 90.
Each of the two other angles is of measure 45.
Therefore sides opposite to two equal angles are equal.
Thus, we may classify the triangle in two different
ways as follows:
(i) Triangle is a right-angled triangle.
(ii) Triangle is an isosceles triangle.
Question 46:
Find angle x in each figure:
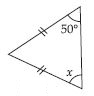
Answer:
Given triangle is isosceles
x = 40
[ Angles opposite to two equal sides of an isosceles triangle are equal]
x = 40
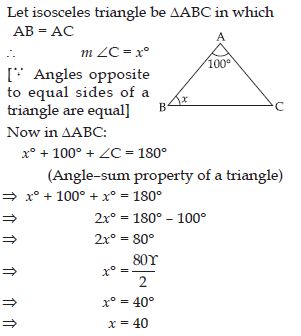
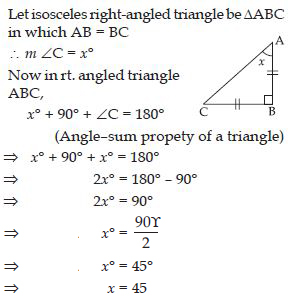
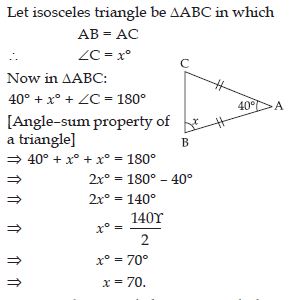
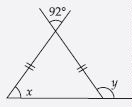
Question 47:
Find angle x in each figure:
Answer:
Let isosceles triangle be ABC in which
AB = AC
m A = 45
[ Angles opposite to equal sides of an isosceles
triangle are equal]
Now in ABC:
x + A + 45 = 180
(Angle–sum property of a triangle)
x + 45 + 45 = 180
[ A = 45 as found above]
x = 180– 45 – 45
x= 90
x = 90
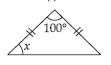
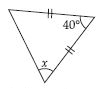
Question 48:
Find angle x in each figure:
Answer:
x = 50
[ Angles opposite to equal sides of an isosceles triangle are equal]
x = 50
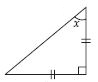
Question 49:
Find angle x in each figure:
Answer:
Question 50:
Find angle x in each figure:
Answer:
Question 51:
Find angle x in each figure:
Answer:
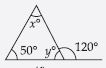
Question 52:
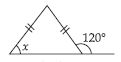
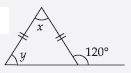
Find angle x in each figure:
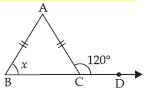
Answer:
Let isosceles triangle be DABC such that
AB = AC
ACB and ACD
form a linear pair.
Therefore,
ACB + 120 = 180
C = 180 – 120
C = 60
Now, AB = AC implies that
x = C
x = 60
[ Angles opposite to equal sides of a triangle are equal]
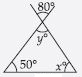
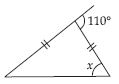
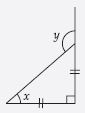
Question 53:
Find angle x in each figure:
Answer:
Let isosceles triangle be ABC in which
AB = AC
B = x
[ Angles opposite to equal sides of a triangle are always equal]
Also, we have
B + x = 110
[ Exterior angle of a triangle is equal to the sum of its interior opposite
angles]
x + x = 110
2x = 110
x = 110/2
x = 55
x = 55
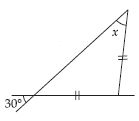
Question 54:
Find angle x in each figure:
Answer:
Let isosceles triangle be DABC in which
AB = BC
In fig., BAC = 30
[Vertically opposite angles]
Now in ABC; we have
AB = BC
x = BAC
[ Angles opposite to equal sides of a triangle are equal]
x = 30
[BAC = 30 as found above]
x = 30
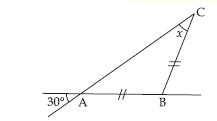
Question 55:
Find angles x and y in each figure.
Answer:
Question 56:
Find angles x and y in each figure.
Answer:
Question 57:
Find angles x and y in each figure.
Answer:
Question 58:
Is it possible to have a triangle with the sides 2 cm, 3 cm, 5 cm?
Answer:
Given sides are 2 cm, 3 cm and 5 cm
Now, 2 + 3 = 5 ...(1)
3 + 5 > 2
5 + 2 > 3
of (1), it is not possible
Question 59:
Is it possible to have a triangle with the sides 3 cm, 6 cm, 7 cm?
Answer:
Given sides are 3 cm, 6 cm, 7 cm
Now, 3 + 6 > 7
6 + 7 > 3
7 + 3 > 6
Sum of the lengths of any two sides would be greater than the length of the third
side.
Question 60:
Is it possible to have a triangle with the sides 6 cm, 3 cm, 2 cm?
Answer:
Given sides are 6 cm, 3 cm, 2 cm
Now, 6 + 3 > 2
3 + 2 < 6
of this, it is not possible.
Question 61:
Take any point O in the interior of a triangle PQR. Is
(i) OP + OQ > PQ?
(ii) OQ + OR > QR?
(iii) OR + OP > RP?
Answer:
(i) Yes, OP + OQ > PQ because sum of the lengths of any two sides of POQ is always greater than the third side.
(ii) Yes, OQ + OR > QR because sum of the lengths of any two sides of ROQ is always greater than the third side.
(iii) Yes, OR + OP > RP because sum of the lengths of any two ides of ROP is always greater than the third.
Question 62:
AM is a median of a triangle ABC. Is AB + BC + CA > 2 AM?
Answer:
Yes; AB + BC + CA > 2 AM
Proof: In ABM; AB + BM > AM ...(i)
[ Sum of the lengths of any two sides of a triangle is greater than the third
side]
In ACM; AC + MC > AM ...(ii)
[using same reason as above]
Adding (i) and (ii), we get:
(AB + BM) + (AC + MC) > AM + AM
or AB + (BM + MC) + AC > 2 AM
or AB + BC + AC > 2 AM
[ AM is the median of triangle ABC
BM = MC. Also M is a point on BC
BC = BM + MC]
Question 63:
ABCD is a quadrilateral. Is AB + BC + CD + DA > AC + BD?
Answer:
Yes; AB + BC + CD + DA > AC + BD
Proof: In ABC; AB + BC > AC ...(i)
[ Sum of lengths of any two sides of a triangle is always greater than the third side]
In ADC; CD + DA > AC ...(ii)
(using same reason as above)
In ABD; AB + DA > BD ...(iii)
(using same reason as above)
In BCD; BC + CD > BD ...(iv)
(using same reason as above)
Adding (i), (ii), (iii) and (iv), we get:
(AB + BC) + (CD + DA) + (AB + DA) + (BC + CD) > AC + AC + BD + BD
or (AB + AB) + (BC + BC) + (CD + CD) +
(DA + DA) > 2AC + 2BD
or 2AB + 2BC + 2CD + 2DA > 2AC + 2BD
or 2 (AB + BC + CD + DA) > 2 (AC + BD)
or AB + BC + CD + DA > AC + BD.
Question 64:
ABCD is quadrilateral. Is AB + BC + CD + DA < 2 (AC + BD)?
Answer:
Yes; AB + BC + CD + DA < 2 (AC + BD)
Proof: In quadrilateral ABCD; let diagonals AC and BD interset each other at point
O.
Now in AOB, AO + OB > AB .... (i)
[ sum of the lengths of any two sides of a triangle is greater than the third
side]
Similarly in BOC;
OB + OC > BC ...(ii)
(using same reason as above)
In COD;
OC + OD > CD ...(iii)
(using same reason as above)
Also in AOD;
AO + OD > DA ...(iv)
(using same reason as above)
Adding (i), (ii), (iii) and (iv), we get:
(AO + OB) + (OB + OC) + (OC + OD) + (AO + OD) > AB + BC + CD + DA
2 (AO + OB + OC + OD) > AB + BC + CD + DA
2 [(AO + OC) + (OB + OD)] > AB + BC + CD + DA
2 [AC + BD] > AB + BC + CD + DA
or AB + BC + CD + DA < 2 (AC + BD) Proved.
Question 65:
The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side be fall?
Answer:
If x can be the length of the third side, we should have:
The length cannot be negative. Therefore we reject it.
Thus, the numbers between 3 and 27 satisfy
these.
The length of the third side could be any
length between 3 cm and 27 cm.
Question 66:
Is the sum of any two angles of a triangle always greater than the third angle?
Answer:
No; this is not the condition required to draw a
triangle. Based on the angles, the only condition
to draw a triangle is that the sum of three angles
of a triangle should be 180.
For example: If we consider three angles as
50, 30, and 100. We have 50 + 30 + 100 but
triangle with these angles is possible to draw
because 50 + 30 + 100 = 180; angle-sum
property is satisfied.
Question 67:
PQR is a triangle, right angled at P. If PQ =
10 cm and PR = 24 cm, find QR.
Answer:
Question 68:
ABC is a triangle right-angled at C. If AB =
25 cm and AC = 7 cm, find BC.
Answer:
Question 69:
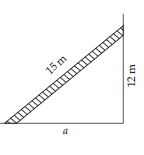
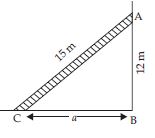
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at distance a (See fig.) Find the distance of the foot of the ladder from the wall.
Answer:
Let the ladder be AC where C is the foot of
the ladder and A be the top of ladder at
12 m high from the ground. Wall is a rt. angled
to the ground at point B.
Now in rt. angled triangle ABC; using
Pythagoras property;
Question 70:
Which of the following can be the sides of a
right triangle?
2.5 cm, 6.5 cm, 6 cm.
In the case of right-angled triangles identify
the right angles.
Answer:
Therefore the triangle with given sides is
a rig ht-angled triangle.
In this right-angled triangle; the longest
side with length 6.5 cm is the hypotenuse
and angle opposite to this side is the right
angle.
Question 71:
Which of the following can be the sides of a
right triangle?
2 cm, 2 cm, 5 cm.
In the case of right-angled triangles identify
the right angles.
Answer:
Question 72:
Which of the following can be the sides of a
right triangle?
1.5 cm, 2 cm, 2.5 cm.
In the case of right-angled triangles identify
the right angles.
Answer:
Question 73:
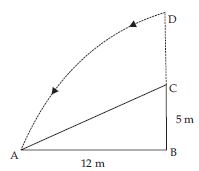
A tree is broken at a height of 5 m from the
ground and its top touches the ground at a
distance of 12 m from the base of the tree.
Find the original height of the tree.
Answer:
Let the original height of tree be BD and tree is broken at point C; at a height of 5 m from the ground.
Let top of the tree D touches the ground at point
A, 12 m away from the base of the tree.
Since it form a right-angled triangle;
ABC right-angled at point B.
Now using Pythagoras property,
Question 74:
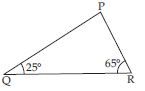
Angles Q and R of a PQR are 25 and 65.
Write which of the following is true:
(i) PQ2 + QR2 = RP2
(ii) PQ2 + RP2 = QR2
(iii) RP2 + QR2 = PQ2
Answer:
In PQR ;
P + Q + R = 180
[Angle-sum property of a triangle]
P + 25 + 65 = 180
P = 180 – 25 – 65
P = 90
It implies that PQR is right-angled triangle
right angled at point P.
As we know that the side opposite to the
right angle is the hypotenuse so side QR is the
hypotenuse.
Using Pythagoras property in rt. angled triangle
PQR,
we have PQ2 + RP2 = QR2
Hence, option (ii); PQ2 + RP2 = QR2 is true.
Question 75:
Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
Answer:
Perimeter of rectangle ABCD = 2 (length + breadth)
= 2 (AB + BC)
= 2 (40 + 9)
= 2 × 49
= 98 cm.
Question 76:
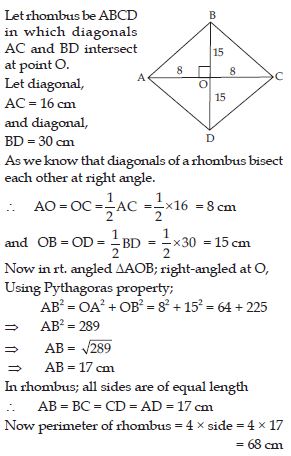
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
Answer:
Question 77:
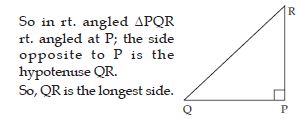
Which is the longest side in the triangle PQR, right angled at P?
Answer:
As we know that in any right-angled triangle; the hypotenuse is the longest side.
Question 78:
Which is the longest side in the triangle ABC right-angled at B?
Answer:
In ABC right-angled at B the side opposite to
B is the hypotenuse AC.
As we know that hypotenuse is the longest side.
So, AC is the longest side.
Question 79:
Which is the longest side of a right-triangle?
Answer:
Hypotenuse is the longest side of a right triangle.
Question 80:
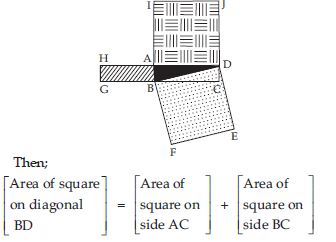
‘‘The diagonal of a rectangle produce by itself the same area as produced by its length and breadth’’. This is Baudhayan Theorem. Compare it with the Pythagoras property.
Answer:
Pythagoroas property gives the relation between the lengths of the sides of a right triangle. According to the Pythagoras property:
‘‘The square described on the hypotenuse has an area equal to the sum of the areas of the squares described on its other two legs. In the given fig., ABC is right-angled triangle right angled at C.
An Indian mathematician Baudhayan gave an
equivalent form of this property and stated the
theorem in its most general form.
According to the Baudhayan theorem:
‘‘The square descirbed on the diagonal of a
rectangle has an area equal to the sum of the
areas of the squares described on its two sides.
In the given fig. ABCD is a rectangle.