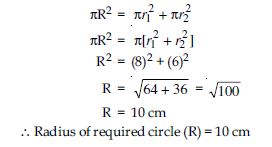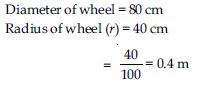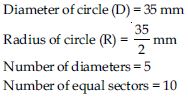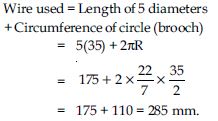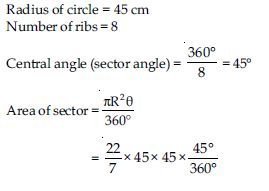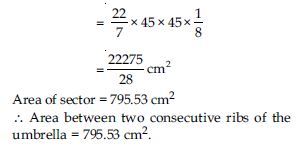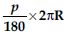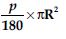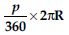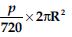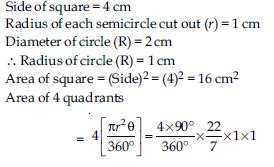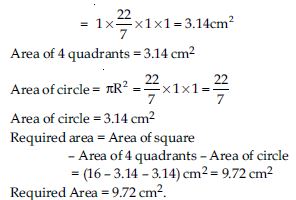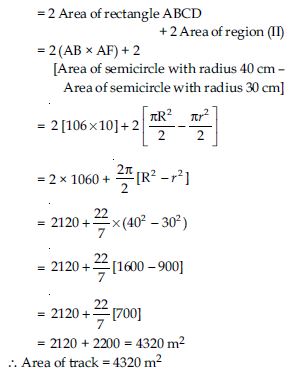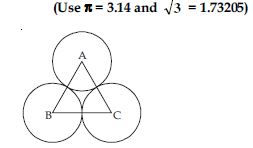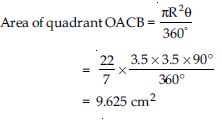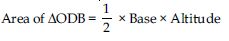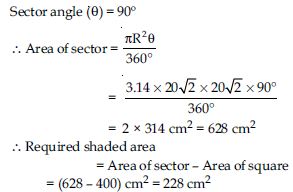Aasoka is an online learning platform that provides top-quality educational resources including NCERT Solutions for Class 10th. The study material is helpful in getting a better grasp of the concepts included in the chapter. The entire chapter is covered accurately and students can easily rely on the NCERT Solutions to clear their exams successfully. These solutions will clear all doubts of students of Class 10th related to any topic of the chapter “Areas Related to Circles”. Grab the latest solutions now and kick start your learning journey.
Students will learn about the area of a circle and its perimeter from the chapter “Areas Related to Circles”. The chapter helps in understanding the segment of a circle, the area of a sector, and the areas of the figures that contain a part of a circle or a circle.
Question 1:
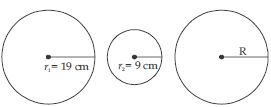
The radii of two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has circumference equal to the sum of the circumferences of the two circles.
Answer:
Radius of first circle (r1) = 19 cm
Radius of second circle (r2) = 9 cm
Let radius of third circle be R cm.
According to question,
Circumference of first circle
+ Circumference of second circle
= Circumference of third circle
2r1 + 2r2 = 2R
2 [r1 + r2] = 2R
19 + 9 = R
∴ R = 28
∴ Radius of third circle (R) = 28 cm
Question 2:
The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of two circles.
Answer:
Radius of first circle (r1) = 8 cm
Radius of second circle (r2) = 6 cm
Let radius of third circle be R cm.
According to question,
Area of third circle = Area of first circle
+ Area of second circle
Question 3:
Fig., depicts an archery target marked with its five scoring regions from the centre outwards as Gold, Red, Blue, Black and White. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.
Answer:
∴ Area of Red region = 1039.5 cm2
[Area of Blue scoring region] = [Combined area
of Red, Blue and Gold region] − [Combined area
of Gold and Red region]
Question 4:
The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour?
Answer:
Question 5:
Tick the correct answer in the following and justify your choice: If the perimeter and area of a circle are numerically equal, then the radius of the circle is
- 2 units
- units
- 4 units
- 7 units
Answer:
(i) 2 units
Question 6:
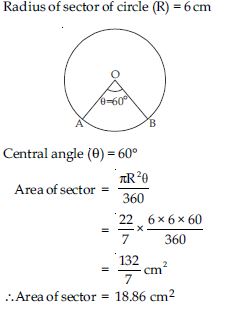
Find the area of a sector of a circle with radius 6 cm, if angle of the sector is 60.
Answer:
Question 7:
Find the area of a quadrant of a circle whose circumference is 22 cm.
Answer:
Question 8:
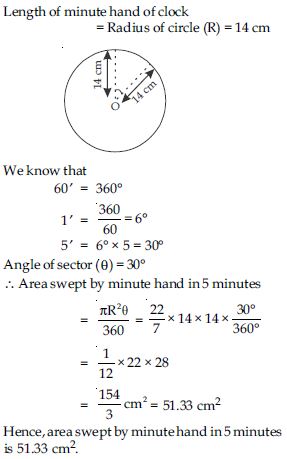
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.
Answer:
Question 9:
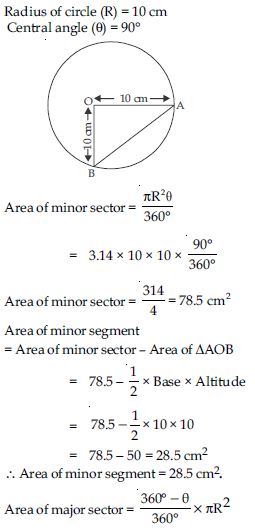
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding: (i) minor segment (ii) major sector. (Use = 3.14)
Answer:
Question 10:
In a circle of radius 21 cm, an arc subtends an angle of 60 at the centre. Find : (i) the length of the arc (ii) area of the sector formed by the arc (iii) area of the segment formed by the corresponding chord.
Answer:
Radius of circle (R) = 21 cm
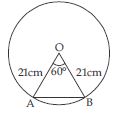
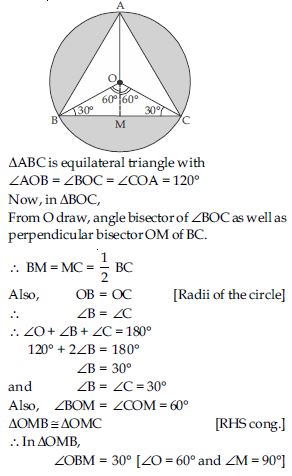
Question 11:
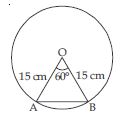
Answer:
Radius of circle = (R) = 15 cm
Central angle () = 60
In ΔOAB, central angle = 60
OA = OB = 15 cm
∴ A = B
Now, A + B + O = 180
2A + 60 = 180
A = 60
∴ A = B = 60
∴ ΔOAB is equilateral triangle.
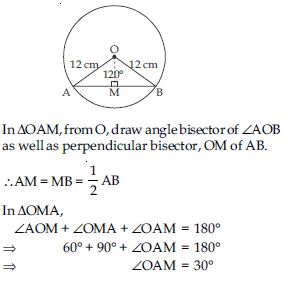
Question 12:
Answer:
Radius of circle (R) = 12 cm
Central angle () = 120
= 150.72 – 36 × 1.73
= (150.72 – 62.28) cm2 = 88.44 cm2
∴ Area of the segment = 88.44 cm2.
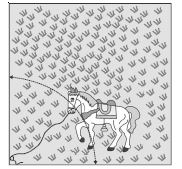
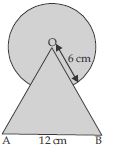
Question 13:
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see fig.). Find : the area of that part of the field in which the horse can graze.
Answer:
Side of square = 15 m
Length of Peg = Radius of rope (R) = 5 m
Central angle () = 90
[Each angle of square]
Question 14:
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see fig.). Find :
the increase in the grazing area if the rope were 10 m long instead of 5 m. (Use = 3.14)
Answer:
Side of square = 15 m
Length of Peg = Radius of rope (R) = 5 m
Central angle () = 90
[Each angle of square]
Question 15:
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means
of a 5 m long rope (see fig.). Find :
the increase in the grazing area if the rope
were 10 m long instead of 5 m. (Use = 3.14)
Answer:
Question 16:
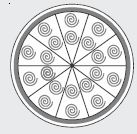
A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in fig. Find : the total length of the silver wire required.
Answer:
Question 17:
A brooch is made with silver wire in the form
of a circle with diameter 35 mm. The wire is
also used in making 5 diameters which divide
the circle into 10 equal sectors as shown in
fig. Find :
the area of each sector of the brooch.
Answer:
Question 18:
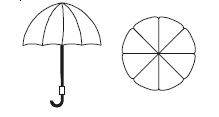
An umbrella has 8 ribs which are equally spaced (see fig.). Assuming umbrella to be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the umbrella.
Answer:
Question 19:
A car has two wipers which do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of 115. Find the total area cleaned at each sweep of the blades.
Answer:
Length of blade (R) = 25 cm
Sector angle () = 115
Wiper moves in form of sector.
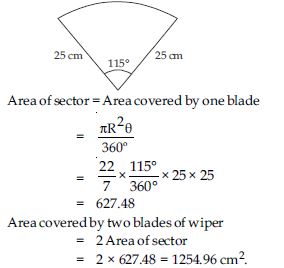
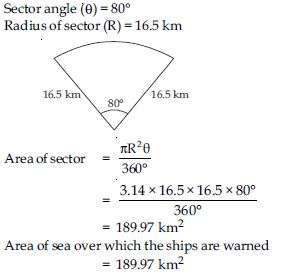
Question 20:
To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80 to a distance of 16.5 km. Find the area of the sea over which the ships are warned. (Use = 3.14)
Answer:
Question 21:
Answer:
Question 22:
Area of a sector of angle p (in degrees) of a circle with radius R is
Answer:
(iv)
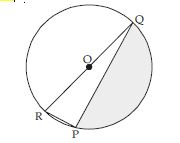
Question 23:
Find the area of the shaded region in fig., if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.
Answer:
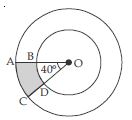
Question 24:
Find the area of the shaded region in fig., if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and AOC = 40.
Answer:
Radius of smaller circle (r) = 7 cm Radius of bigger circle (R) = 14 cm Central angle AOC () = 40
Question 25:
Find the area of the shaded region in fig., if ABCD is a square of side 14 cm and APD and BPC are semicircles.
Answer:
Question 26:
Find the area of the shaded region in fig., where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre.
Answer:
Question 27:
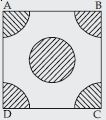
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in fig. Find the area of the remaining portion of the square.
Answer:
Question 28:
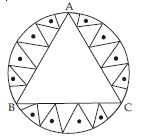
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in fig. Find the area of the design.
Answer:
Radius of table cover (R) = 32 cm
OA = OB = OC = 32 cm
Question 29:
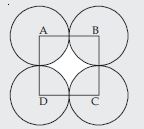
In fig., ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.
Answer:
Question 30:
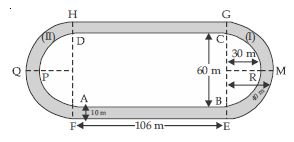
Fig. depicts a racing track whose left and right ends are semicircular.
The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find: the distance around the track along its inner edge.
Answer:
Question 31:
Fig. depicts a racing track whose left and right ends are semicircular.
The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
Answer:
Area of track
= Area of rectangle ABEF
+ Area of region BEMGCRB
+ Area of rectangle CGHD
+ area of region (II).
Question 32:
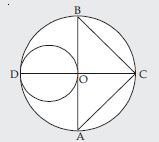
In fig., AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
Answer:
Question 33:
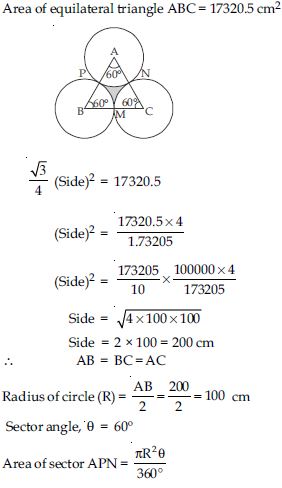
The area of an equilateral triangle ABC is
17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with
radius equal to half of the length of the side of the triangle (see fig.). Find the area of
the shaded region.
Answer:
Question 34:
On a square handkerchief, nine circular designs each of radius 7 cm are made (see fig.). Find the area of the remaining portion of the handkerchief.
Answer:
Question 35:
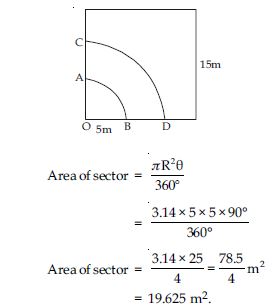
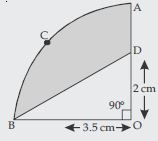
In fig., OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the quadrant OACB,
Answer:
Radius of quadrant (R) = 3.5 cm
Sector angle () = 90º
OD = 2 cm.
Question 36:
In fig., OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.
Answer:
Radius of quadrant (R) = 3.5 cm
Sector angle () = 90º
OD = 2 cm.
Question 37:
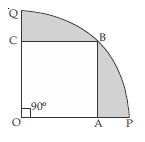
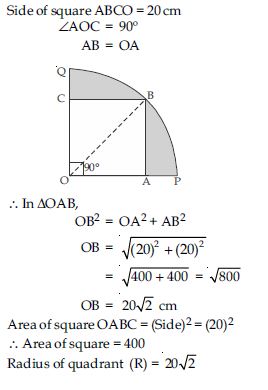
In fig., a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use = 3.14)
Answer:
Question 38:
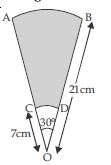
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see fig.) If ∠AOB = 30º, find the area of the shaded region.
Answer:
Question 39:
In fig., ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
Answer:
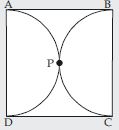
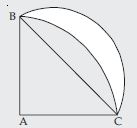
Question 40:
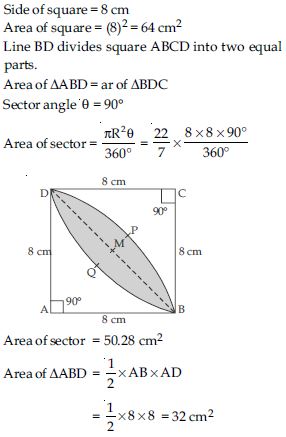
Calculate the area of the designed region in fig., common between the two quadrants of circles of radius 8 cm each.
Answer:
∴ Area of segment DMBPD
= Area of sector ABPD – Area of ABD
= 50.28 – 32
= 18.28 cm2
Hence, shaded area
= 2 area of segment DMBPD
= 2 (18.28) = 36.57 cm2