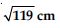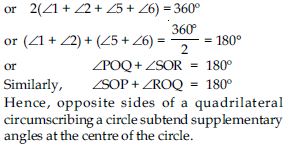Get free access to top NCERT Solutions for Class 10th prepared by the experts after thorough research. These researchers have kept in mind the latest syllabus and exam pattern while designing the solutions. Students can easily study from the NCERT Solutions at Aasoka and prepare for their board examinations. The preparations are made efficient and effective with these solutions available at Aasoka, the best online learning platform for students.
The chapter “Circle” of Class 10th Math introduced the concept of circle, chord, arc, tangent, number of tangents from a point on a circle, cyclic quadrilaterals, the angle subtended by the arc of a circle, and so much more.
Question 1:
How many tangents can a circle have?
Answer:
Since at any point on a circle, there can be one and only one tangent. But circle is a collection of infinite points, so we can draw infinite number of tangents to a circle.
Question 2:
A tangent to a circle intersects it in ______ point(s).
Answer:
one
Question 3:
A line intersecting a circle in two points is called a ______.
Answer:
secant
Question 4:
A circle can have ______ parallel tangents at the most.
Answer:
two
Question 5:
The common point of a tangent to a circle and the circle is called ______.
Answer:
point of contact
Question 6:
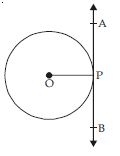
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is:
- 12 cm
- 13 cm
- 8.5 cm
-
Answer:
(iv)
Question 7:
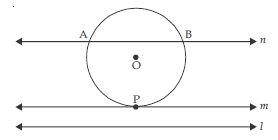
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Answer:
According to the given information we draw a circle having O as centre and l is the given line.
Now, m and n be two lines parallel to a given line l such that m is tangent as well as parallel to l and n is secant to the circle as well as parallel to l.
Question 8:
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
- 7 cm
- 12 cm
- 15 cm
- 24.5 cm
Answer:
(i) 7 cm
Question 9:
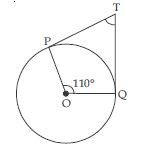
In fig., if TP and TQ are two tangents to a circle with centre O so that POQ = 110, then PTQ is equal to
- 60
- 70
- 80
- 90
Answer:
(ii) 70
Question 10:
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80, then POA is equal to
- 50
- 60
- 70
- 80
Answer:
(i) 50
Question 11:
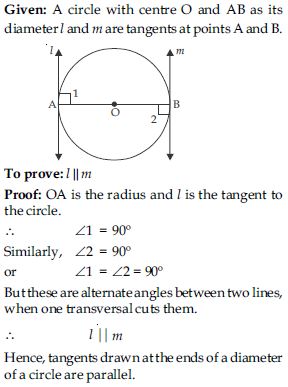
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Answer:
Question 12:
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Answer:
Given: A circle with centre O. Its tangent AB meets circle at P. i.e., P is the point of contact. To prove: Perpendicular at the point of contact to the tangent to a circle passes through the centre.
Construction: Join OP. Proof: The perpendicular to a tangent line AB through the point of contact passes through the centre of the circle because only one perpendicular, OP can be drawn to the line AB through the point P.
Hence, perpendicular at the point of contact to the tangent to a circle passes through the centre.
Question 13:
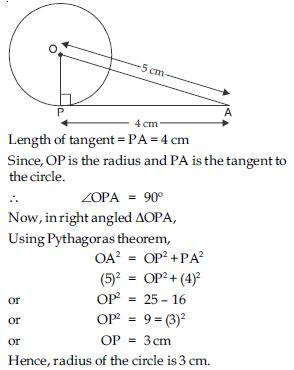
The length of a tangent from a point A at a distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Answer:
A circle with centre ‘O’. A is any point outside the circle at a distance of 5 cm from the centre.
Question 14:
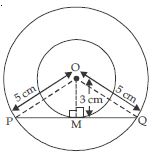
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Answer:
Two concentric circles having same centre O, and radii 5 cm and 3 cm respectively. Let PQ be the chord of larger circle but tangent to the smaller circle.
Question 15:
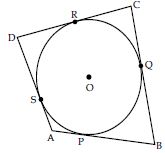
A quadrilateral ABCD is drawn to circumscribe a circle (see figure). Prove that AB + CD = AD + BC.
Answer:
Given: A quadrilateral ABCD is drawn to
circumscribe a circle having O as its centre.
To prove: AB + CD = AD + BC
Proof: Since, the lengths of tangents drawn from
an external point to a circle are equal.
Now, B is any point outside the circle and BQ;
BP are tangents to the circle.
∴ BQ = BP ...(1)
Similarly, AS = AP ...(2)
and CQ = CR ...(3)
Also, DS = DR ...(4)
Adding (1), (2), (3) and (4), we get
(BQ + CQ) + (AS + DS) = (BP + AP) + (CR + DR)
BC + AD = AB + CD
is the required result.
Question 16:
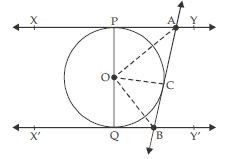
In figure, XY and X′Y′ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X′Y′ at B. Prove that AOB = 90.
Answer:
Given: A circle with centre O having two
parallel tangents XY and X′Y′, another tangent
AB with point of contact C intersecting XY at A
and X′Y′ at B.
To prove: AOB = 90
Construction: Join OC, OA and OB.
Proof: Since, the lengths of tangents drawn from
an external point to a circle are equal.
Now, A is any point outside the circle from two
tangents PA and CA are drawn to the circle.
∴ PA = CA
Also, in POA and AOC,
PA = CA (Proved)
OA = OA (Common side)
OP = OC (Radii of same circle)
∴ POA AOC [SSS congruence]
and PAO = CAO [CPCT]
or PAC = 2 PAO = 2 CAO ...(1)
Similarly,
QBC = 2OBC = 2 OBQ ...(2)
Now, PAC + QBC = 180
[Sum of the interior angles on the same side of
transversal is 180.]
Question 17:
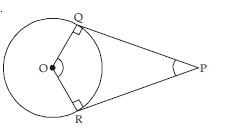
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
Answer:
Given: A circle with centre O. P is any point outside the circle from PQ and PR are the tangents to the given circle.
To prove: ROQ + QPR = 180
Proof: OQ is the radius and PQ is tangent from
point P to the given circle.
∴ OQP = 90 ...(1)
[The tangent at any point of a circle is
perpendicular to the radius through the point
of contact.]
Similarly, ORP = 90 ...(2)
Now, in quadrilateral ROQP,
ROQ + PRO + OQP + QPR = 360
or ROQ + 90 + 90 + QPR = 360
[Using (1) & (2)]
or ROQ + QPR + 180 = 360
or ROQ + QPR = 360 – 180 = 180
Hence, the angle between the two tangents drawn
from an external point to a circle is supplementary
to angle subtended by the line segment joining
the points of contact at the centre.
Question 18:
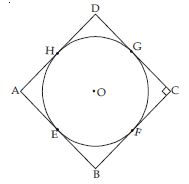
Prove that the parallelogram circumscribing a circle is a rhombus.
Answer:
Given: A parallelogram ABCD circumscribing
a circle with centre O.
Proof: We know that, the lengths of tangents
drawn from an external point to a circle are equal.
Now, B is any point outside the circle and BE,
BF are tangents to the circle.
∴ BE = BF ...(1)
Similarly, AE = AH ...(2)
and CG = CF ...(3)
Also DG = DH ...(4)
Adding (1), (2), (3) and (4), we get
(BE + AE) + (CG + DG) = (BF + CF) + (AH + DH)
or AB + CD = BC + AD ...(5)
Now, ABCD is a parallelogram,
∴ AB = CD and BC = AD ...(6)
From (5) and (6), we get
AB + AB = BC + BC
or 2AB = 2BC or AB = BC
or AB = BC = CD = AD
∴ ABCD is a rhombus.
Hence, parallelogram circumscribing a circle is a rhombus.
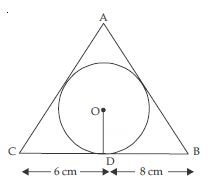
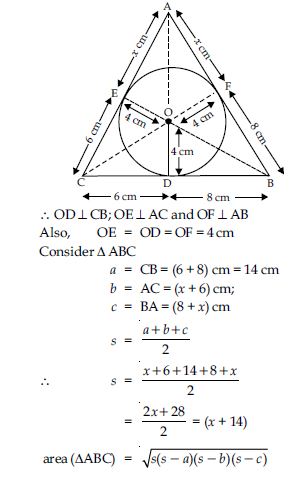
Question 19:
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and C into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see fig.). Find the sides AB and AC.
Answer:
A triangle ABC is drawn to circumscribe a circle
of radius 4 cm and the sides BC, CA, AB of ΔABC
touch the circle at D, E, F respectively. Since, the
lengths of tangents drawn from an external point
to a circle are equal.
∴ AE = AF = x cm (say)
CE = CD = 6 cm
and BF = BD = 8 cm
Since, the tangent at any point of a circle is
perpendicular to the radius through the point
of contact.
Question 20:
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Answer:
Given: A quadrilateral PQRS circumscribing a circle having centre O. Sides PQ, QR, RS and SP touch the circle at L, M, N, T respectively.
To prove: POQ + SOR = 180
and SOP + ROQ = 180
Construction: Join OP, OL, OQ, OM, OR, ON,
OS, OT
Proof: Since, the two tangents drawn from an
external point subtend equal angles at the centre.
∴ 2 = 3; 4 = 5 ; 6 = 7; 8 = 1 ...(1)
But, sum of all angles around a point is 360
∴ 1 + 2 + 3 + 4 + 5
+ 6 + 7 + 8 = 360
or 1 + 2 + 2 + 5 + 5
+ 6 + 6 + 1 = 360