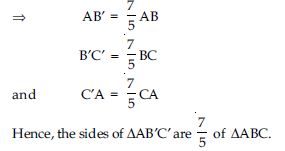Aasoka’s NCERT Solutions provides step-by-step solutions to all questions related to the chapter “Constructions”. The latest syllabus and guidelines are taken into consideration while framing the questions as well as their solutions. Only the current syllabus questions are included so that it is easier for students to prepare for their board exams. The NCERT Solutions for Class 10th can be accessed for free by students to get ready for their exams. So, get started with learning and take your performance to the next level.
“Constructions” is one of the most engaging chapters of Math Class 10th. In this chapter, students will learn how to construct different geometric figures, draw tangents to a circle, and divide a line segment. The chapter includes methods and steps for each method of construction with various examples. The examples are provided before each exercise for a better understanding of the concept.
Question 1:
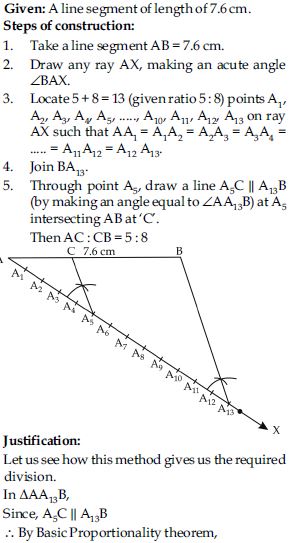
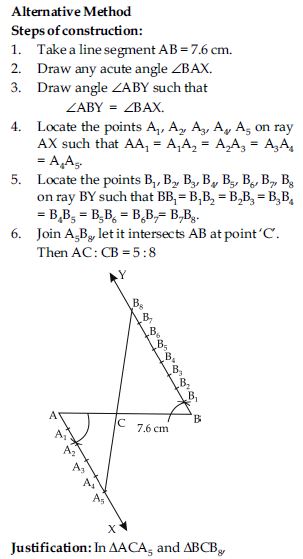
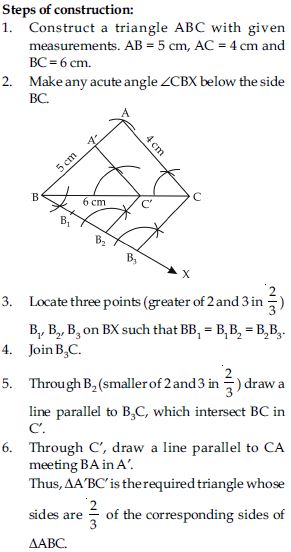
Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts.
Answer:
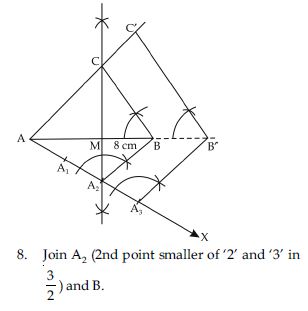
Question 2:
Answer:
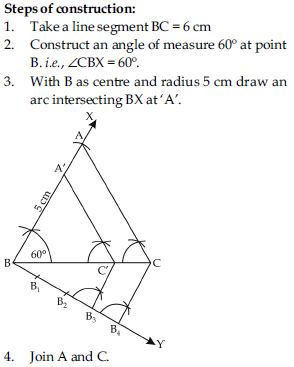
Question 3:
Answer:
Question 4:
Answer:
Question 5:
Answer:
Question 6:
Answer:
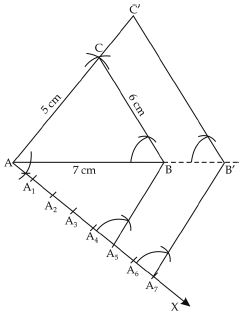
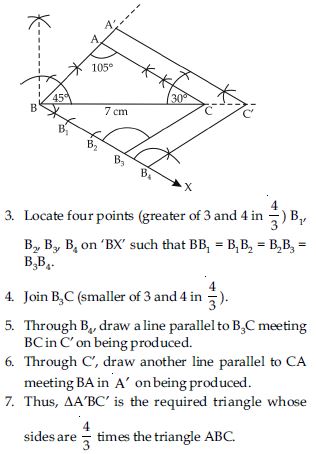
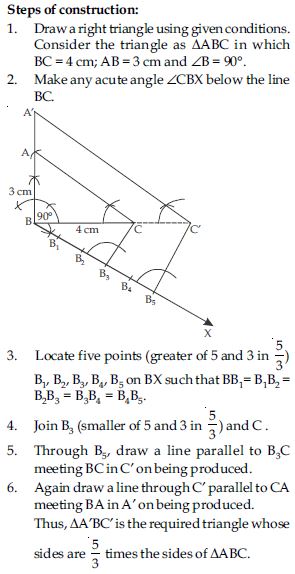
Steps of construction:
1. Construct the triangle ABC with the given
measurements.
BC = 7 cm;
B = 45,
A = 105
By angle sum property of triangle
A + B + C = 180
105 + 45 + C = 180
C = 180 – 150 = 30
2. Make any acute angle CBX at point B,
below the side BC.
Question 7:
Answer:
Question 8:
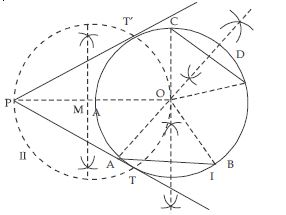
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Answer:
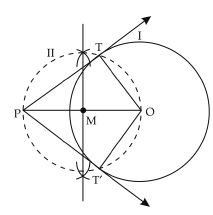
Steps of construction:
1. Draw a circle (I) of radius 6 cm.
2. Take a point P at a distance of 10 cm from
the centre of the circle. Join OP.
3. Draw perpendicular bisector of OP. Let ‘M’
be the mid-point of OP.
4. With ‘M’ as centre and radius MO, draw a
circle (II) which intersects the circle (I) at T
and T′. Join PT and PT′.
5. Then PT and P T′ are two required tangents.
Justification:
We know that a tangent at a point is always
perpendicular to the radius at the point. Now
we have to prove that PTO = PT′O = 90.
OT is joined.
Now, PMO is the diameter of circle (II)
and PTO is in the semicircle.
∴ PTO = 90
[Angle in semicircle is a right angle]
Similarly, PT′O = 90
∴ PT and PT′ have to be the tangents to the
circle at T and T′ .
On measuring, the lengths of tangents
i.e., PT = 8.1 cm
PT′ = 8.1 cm.
Question 9:
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Answer:
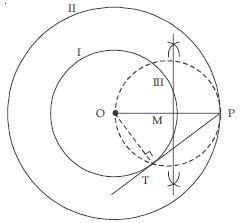
Steps of construction:
1. Draw a circle with centre O and radius
4 cm. Mark it as I.
2. Draw another circle with same centre O and
radius 6 cm and mark it as II.
3. Take any point P on circle II. Join OP.
4. Draw perpendicular bisector of OP. Let it
intersects OP at M.
5. With M as centre and radius MO or MP,
draw a circle III which intersects the circle I
at T and T′.
6. Join PT.
PT is the required tangent.
Justification:
Join OT.
Now OP is the diameter of the circle III.
OTP is in the semicircle.
∴ OTP = 90 ...(1)
[∵ Angle in a semicircle is a right angle]
Now OT ⊥ PT [using (1)]
ä A line which makes an angle of 90 with radius
at any point on the circle, the line is tangent to
the circle.
∴ PT is tangent to the circle ‘I’.
Question 10:
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Answer:
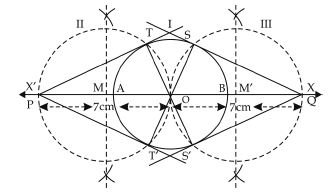
Steps of construction: 1. Draw a circle of radius 3 cm and centre O.
2. Draw its diameter AB and extend it in both
directions as OX and OX′.
3. Take points P on OX′ direction and Q on
OX direction such that
OP = OQ = 7 cm.
4. Draw perpendicular bisectors of OP and OQ
which intersects OP and OQ at M and M′
respectively.
5. With M as centre and radius = MO or MP,
draw a circle II which intersects the circle ‘I’
at T and T′.
6. Similarly, with M′ as centre and radius =
M′O or MQ, draw a circle (III) which
intersects the circle I at S and S′.
7. Join PT, PT′ and QS, QS′.
Justification:
Join OT and OT′ and OS and OS′.
To prove PT and PT′ are tangents to the circle,
we will prove that PTO = PT′O = 90.
Now OP acts as the diameter of circle II and OTP
is in the semicircle.
∴ OTP = 90º ...(1)
[∵ angle in semicircle is 90º]
But OT is the radius of circle I and line PT touches
the circle at T.
ä The line which touches the circle at a point
and makes an angle of 90º with radius at that
point, is tangent to the circle.
∴ PT is tangent to the circle I at point T through
point ‘P’.
Similarly, PT′, QS and QS′ are tangents to the
circle I.
Question 11:
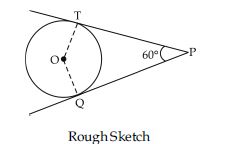
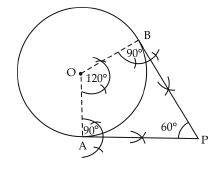
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60.
Answer:
Steps of construction:
1. Draw the rough sketch of required figure.
∵ The tangents make an angle of 60º with each
other.
OTP = OQT = 90º
[Tangent is perpendicular to the radius of circle.]
To find inclination of radii with each other
TOQ + OTP + OQP + TPQ = 360º
[angle sum property of quad.]
or TOQ + 90º + 90º + 60º = 360º
or TOQ = 360º – 90º – 90º – 60º = 120º
2. Draw a circle of radius 5 cm.
3. Draw two radii of circle which make an angle
of 120º with each other.
4. The radii intersect the circle at A and B.
5. Make an angle of 90º at each point A and B,
which intersect each other at P.
6. PA and PB are the required tangents.
Question 12:
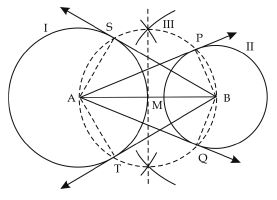
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Answer:
Steps of construction:
1. Draw a line segment AB = 8 cm.
2. With A as centre and radius 4 cm, draw a
circle (I).
3. With B as centre and radius 3 cm, draw a
circle (II).
4. Draw the perpendicular bisector of line
segment AB which intersects AB at M.
5. With M as centre and radius MA or MB,
draw a circle (III) which intersects the circle
(I) at S and T and circle (II) at P and Q.
6. Join AP and AQ. These are required tangents
to the circle with radius 3 cm from point A.
7. Join BS and BT. These are required tangents
to the circle with radius 4 cm from point B.
Justification:
In circle (III), AB acts as diameter then ASB and
BPA are in semicircle.
∴ ASB = 90º ...(1) [angle in semicircle]
and BPA = 90º ...(2)
But ASB is angle between radius of circle (I)
and line segment BS and BPA is angle between
radius of circle (II) and line segment AP.
ä Line segment which is perpendicular to the
radius of circle, is tangent to the circle through
that point.
∴ BS is tangent to circle (I) at point S and AP is
tangent to circle (II) at point P.
Similarly, AQ and BT are tangents to the circle
(II) and (I) respectively.
Question 13:
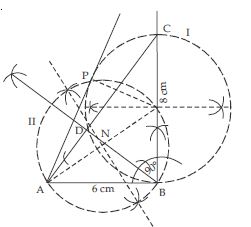
Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and B = 90. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Answer:
Steps of construction:
1. Construct right angled triangle ABC
according to given conditions and
measurements.
2. Draw BD ⊥ AC.
3. Take mid-point of side BC take it as M.
4. Take M as centre and BC as diameter, draw
a circle through B, C, D using property, angle
in semicircle is 90º (BDC = 90º). Take this
circle as I.
5. Now join A and M.
6. Draw perpendicular bisector of AM to cut
AM at N. Now with N as centre and NA or
NM as radius, draw a circle (II) which
intersects the circle (I) at B and P.
7. Join AP.
8. AP and AB are the required tangents.
Justification of construction:
Line segment AM is diameter of circle (II).
APM is in semicircle.
∴ APM = 90º [angle in semicircle]
i.e., MP ⊥ AP
But MP is the radius of circle (I)
∴ AP is tangent to the circle (II)
[∵ any line ⊥ to radius of circle at any point on
the circle is tangent to the circle.]
Similarly, AB is tangent to circle (I).
Question 14:
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
Answer:
To draw circle with bangle means the centre of circle is unknown. First find the centre of circle.
Steps of construction:
1. Draw a circle using a bangle (I).
2. Take any two chords AB and CD (nonparallel)
on circle.
3. Draw the perpendicular bisectors of chords
AB and CD. The perpendicular bisectors
intersect each other at point O.
[∵ any point lying on perpendicular bisector
of line segment is equidistant from its end
points]
[ä O lies on ⊥ bisector of AB and CD]
∴ OA = OB
and OC = OD
∴ OA = OB
OC = OD (radii of circle)
∴ O is the centre of circle.
4. Take any point P outside the circle.
5. Join OP.
6. Draw the perpendicular bisector of OP. Let
M is the mid-point of OP.
7. With M as centre and radius ‘MP’ or ‘MO’,
draw a circle II which intersects the circle (I)
at T and T′.
8. Join PT and PT′, which is required pair of
tangents.
Justification:
Tangent at a point is always perpendicular to
the radius at the point. Now, we have to prove
that PTO = PT′O = 90.
Join OT.
Now PTO is in the semicircle I.
∴ PTO = 90
[angle in semicircle is a right angle]
Similarly, PT′O = 90
∴ PT and PT′ has to be the tangents to the circle
at T and T′.