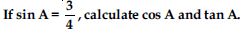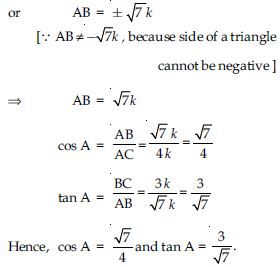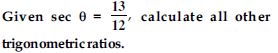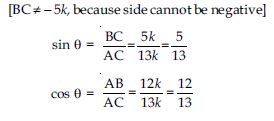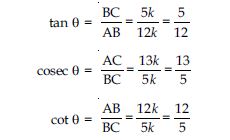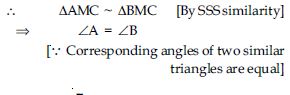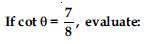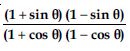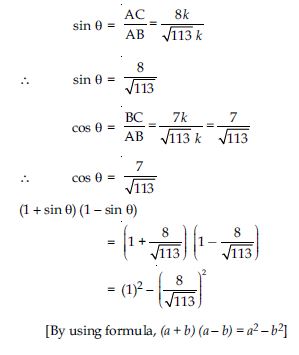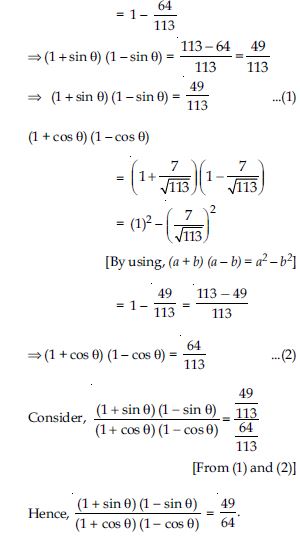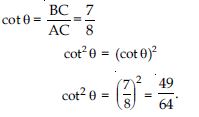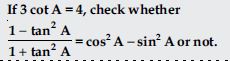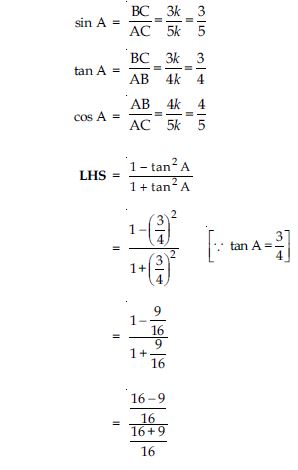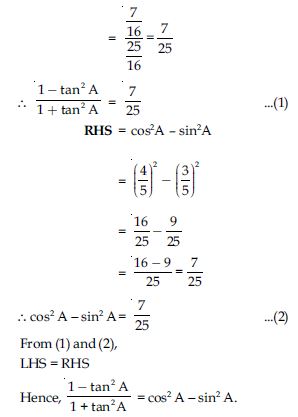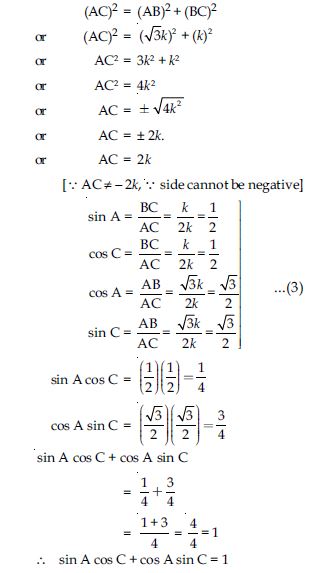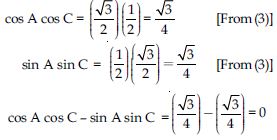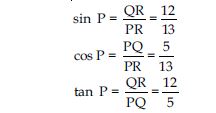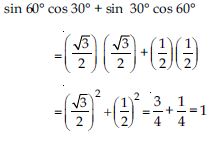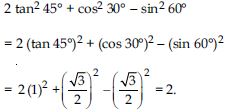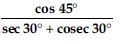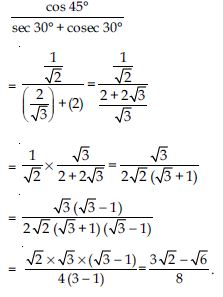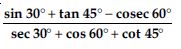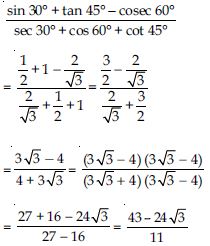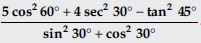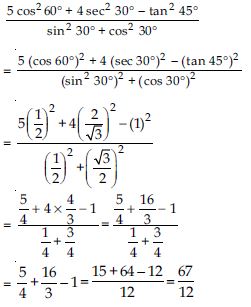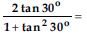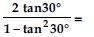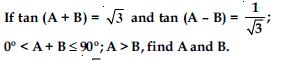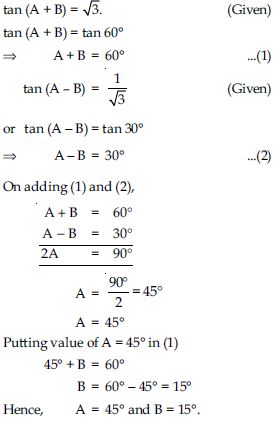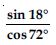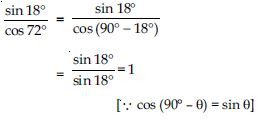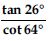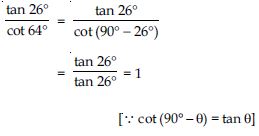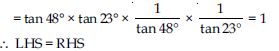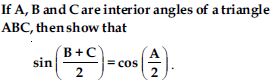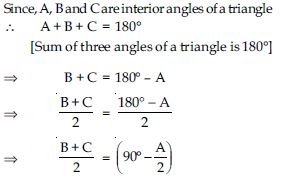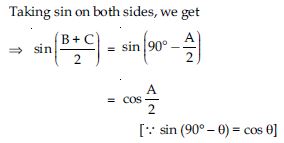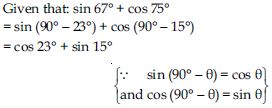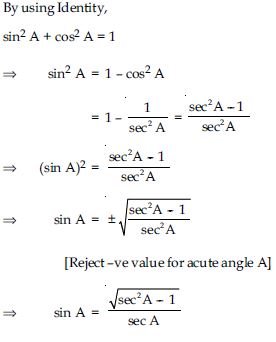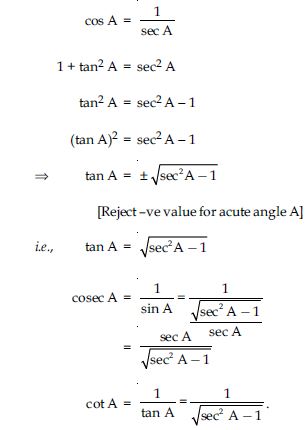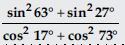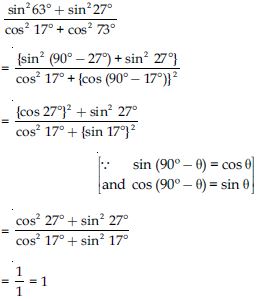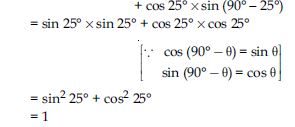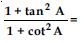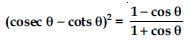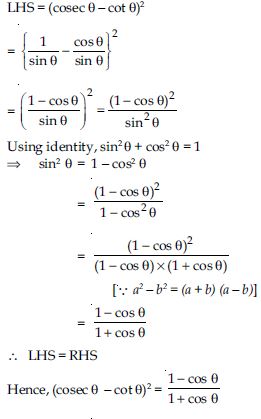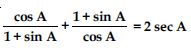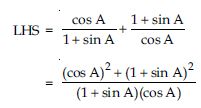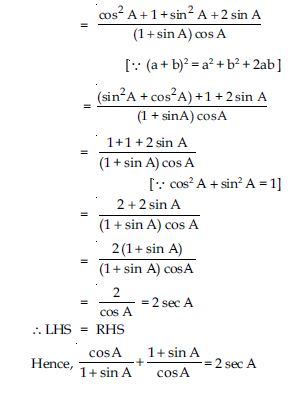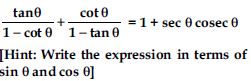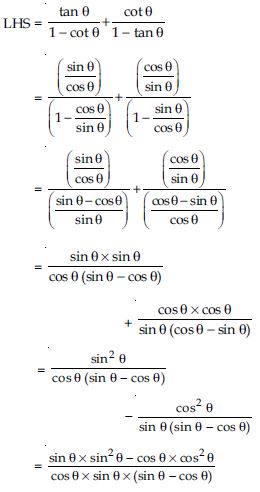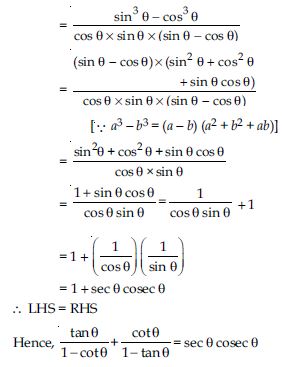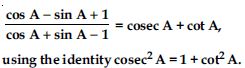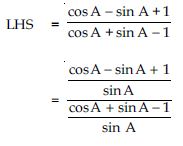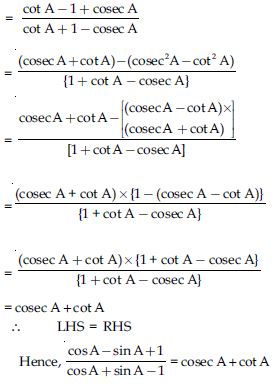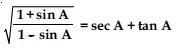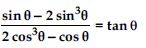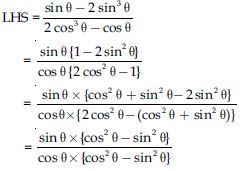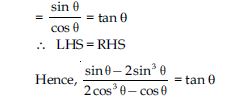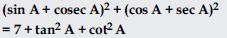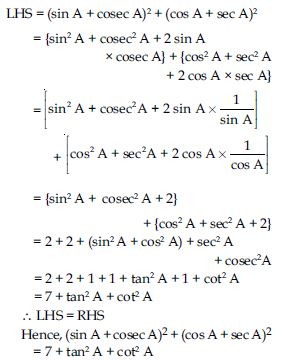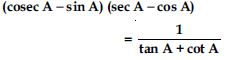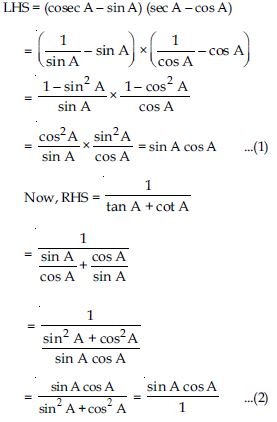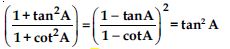NCERT Solutions for Class 10 Math Chapter 8 - Introduction to Trigonometry

Question 1:

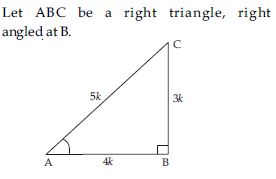
In ΔABC, right-angled at B, AB = 24 cm;
BC = 7 cm. Determine:
(i) sin A, cos A (ii) sin C, cos C

Question 2:

Question 3:

Question 4:

Given 15 cot A = 8, find sin A and sec A.

Question 5:

Question 6:

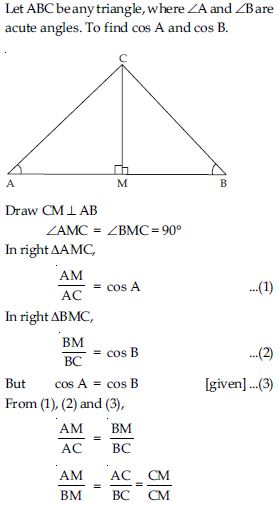
If $\angle$A and $\angle$B are acute angles such that cos A = cos B, then show that: $\angle$A = $\angle$B.

Question 7:

Question 8:

cot² $\mathrm{\theta }$.

Question 9:

Question 10:

sin A cos C + cos A sin C

Question 11:

cos A cos C - sin A sin C.

Question 12:

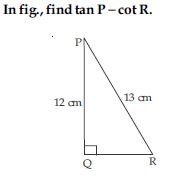
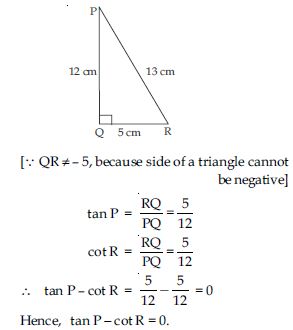
In $∆$PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.

Question 13:

The value of tan A is always less than 1.

Question 14:

Question 15:

cos A is abbreviation used for the cosecant of angle A.

Question 16:

cot A is the product of cot and A.

Question 17:

Question 18:

Evaluate the following:
sin 60$°$ cos 30$°$ + sin 30$°$ cos 60$°$

Question 19:

Evaluate the following:
2 tan² 45$°$ + cos² 30$°$ - sin² 60$°$

Question 20:

Evaluate the following:

Question 21:

Evaluate the following:

Question 22:

Evaluate the following:

Question 23:

1. sin 60$°$
2. cos 60$°$
3. tan 60$°$
4. sin 30$°$

Question 24:

1. tan 90$°$
2. 1
3. sin 45$°$
4. 0

Question 25:

sin 2A = 2 sin A is true when A =

1. 0$°$
2. 30$°$
3. 45$°$
4. 60$°$

Question 26:

1. cos 60$°$
2. sin 60$°$
3. tan 60$°$
4. sin 30$°$

Question 27:

Question 28:

sin (A + B) = sin A + sin B.

Question 29:

The value of sin $\mathrm{\theta }$ increases as $\mathrm{\theta }$ increases.

Question 30:

The value of cos $\mathrm{\theta }$ increases as $\mathrm{\theta }$ increases.

Question 31:

sin $\mathrm{\theta }$ = cos $\mathrm{\theta }$ for all value of $\mathrm{\theta }$.

Question 32:

cot A is not defined for A = 0$°$.

Question 33:

Evaluate:

Question 34:

Evaluate:

Question 35:

Evaluate:
cos 48$°$ - sin 42$°$

Question 36:

Evaluate:
cosec 31$°$ - sec 59$°$.

Question 37:

Show that:
tan 48$°$ tan 23$°$ tan 42$°$ tan 67$°$ = 1

Question 38:

Show that:
cos 38$°$ cos 52$°$ - sin 38$°$ sin 52$°$ = 0

Question 39:

If tan 2A = cot (A - 18$°$), where 2A is an acute angle, find the value of A.

Question 40:

If tan A = cot B, prove that: A + B = 90$°$.

Question 41:

If sec 4A = cosec (A - 20$°$), where 4A is an acute angle, find the value of A.

Question 42:

Question 43:

Express sin 67$°$ + cos 75$°$ in terms of trigonometric ratios of angles between 0$°$ and 45$°$.

Question 44:

Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.

Question 45:

Write all the other trigonometric ratios of $\angle$A in terms of sec A.

Question 46:

Evaluate:

Question 47:

Evaluate:
sin 25$°$ cos 65$°$ + cos 25$°$ sin 65$°$

Question 48:

9 sec² A - 9 tan² A =

1. 1
2. 9
3. 8
4. 0

Question 49:

(1 + tan $\mathrm{\theta }$ + sec $\mathrm{\theta }$) (1 + cot $\mathrm{\theta }$ - cosec $\mathrm{\theta }$) =

1. 0
2. 1
3. 2
4. - 1

Question 50:

(sec A + tan A) (1 - sin A) =

1. sec A
2. sin A
3. cosec A
4. cos A

Question 51:

1. sec²A
2. - 1
3. cot²A
4. tan²A

Question 52:

Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

Question 53:

Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

Question 54:

Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

Question 55:

Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

Question 56:

Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

Question 57:

Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

Question 58:

Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

Question 59:

Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

Question 60:

Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

[Hint: Simplify LHS and RHS separately]

Question 61:

Prove the following identities, where the angles involved are acute angles for which the expressions are defined.