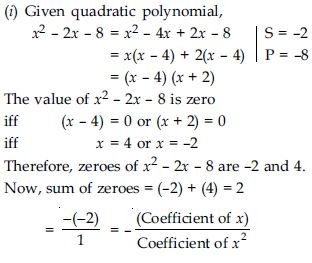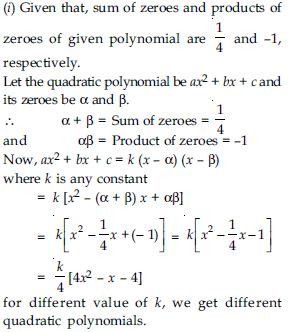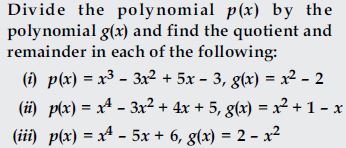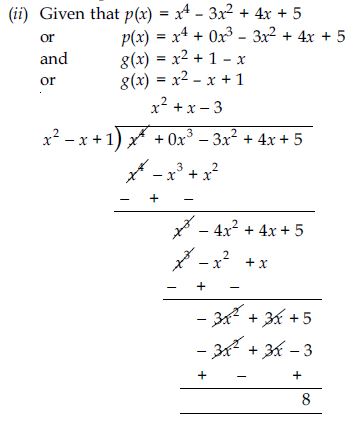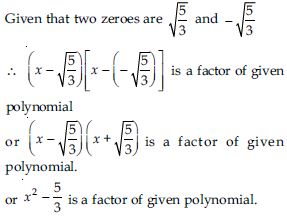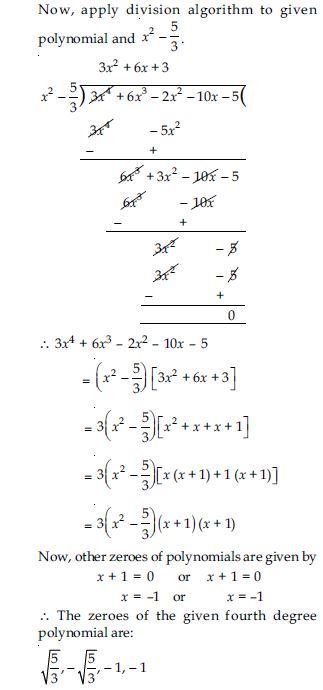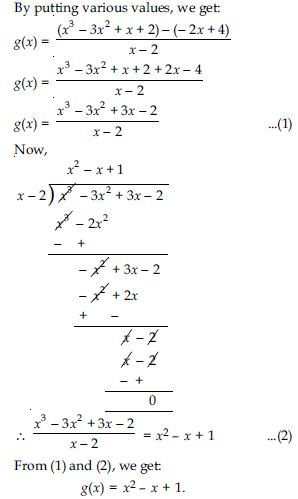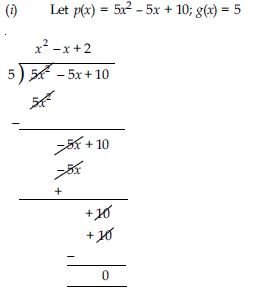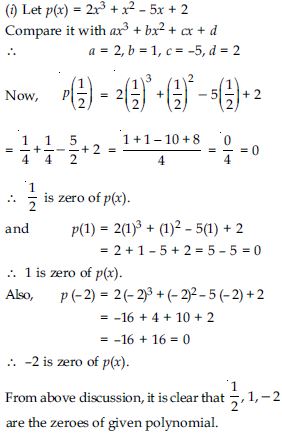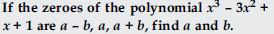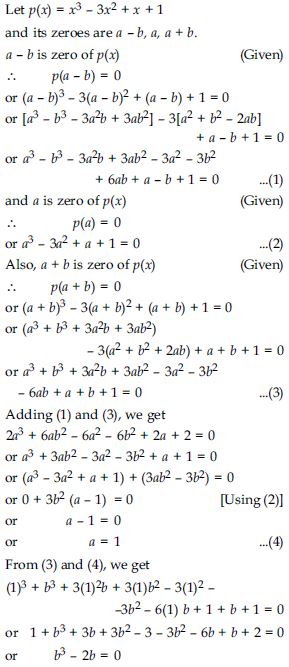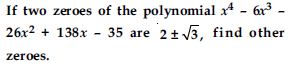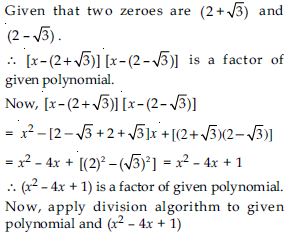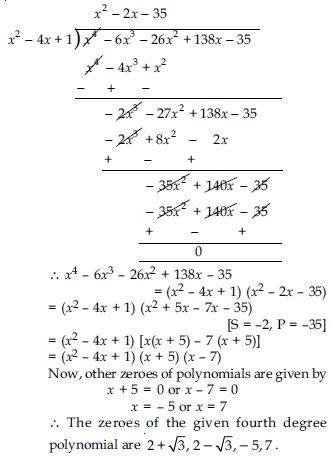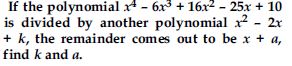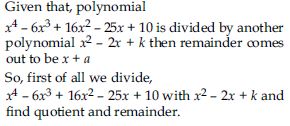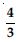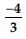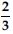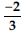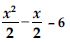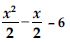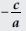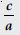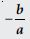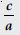For efficient and effective exam preparations, NCERT Solutions at Aasoka is the finest resource. Aasoka is a top online learning platform for students to learn and understand the concept of Math Class 10th. Math is a very crucial subject which if studied properly, would help students in the long run. Along with this, students can easily score good marks in their Math exam with good preparation. Take the help of NCERT Solutions for Class 10th to kick start your learning process.
“Polynomial” is a chapter in Class 10th Math that provides the explanation of linear polynomial, cubic polynomial, degree of the polynomial, and quadratic polynomial. The chapter consists of 4 exercises to help students understand the chapter properly. The first exercise has questions related to a graph where students have to find the number of zeroes. To solve this exercise, students need to know about the geometrical meaning of the zeroes of a polynomial. The second exercise includes questions related to quadratic polynomials. Exercise 2.3 consists of the questions based on the division algorithm. And the last exercise has questions from all the topics of Math Chapter 2.
Question 1:
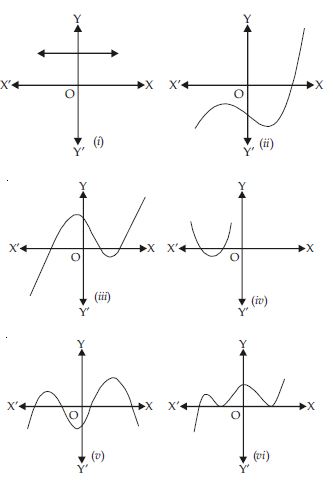
The graphs of y = p(x) are given in figure below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.
Answer:
The graphs of y = p(x) are given in figure, for some polynomials p(x). The number of zeroes of p(x) in each case are given below:
- From the graph, it is clear that it does not meet x-axis at any point.
Therefore, it has no. of zeroes = 0
- From the graph, it is clear that it meets x-axis at only one point.
Therefore, no. of zeroes = 1
- From the graph, it is clear that it meets x-axis at three points.
Therefore, no. of zeroes = 3
- From the graph, it is clear that it meets x-axis at two points.
Therefore, no. of zeroes = 2
- From the graph, it is clear that it meets x-axis at four points.
Therefore, no. of zeroes = 4
- From the graph, it is clear that it meets x-axis at three points.
From the graph, it is clear that it meets x-axis at three points.
Question 2:
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
- x2 - 2x - 8
- 4s2 - 4s + 1
- 6x2 - 3 - 7x
- 4u2 + 8u
- t2 - 15
- 3x2 - x - 4
Answer:
Question 3:
Answer:
Question 4:
Answer:
Question 5:
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial.
- t2 - 3, 2t4 + 3t3 - 2t2 - 9t - 12
- x2 + 3x + 1, 3x4 + 5x3 - 7x2 + 2x + 2
- x3 - 3x + 1, x5 - 4x3 + x2 + 3x + 1
Answer:
Question 6:
Answer:
Question 7:
On dividing x3 - 3x2 + x + 2 by a polynomial g(x), the quotient and remainder were x - 2 and -2x + 4 respectively, find g(x).
Answer:
Question 8:
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
- deg p(x) = deg q(x)
- deg q(x) = deg r(x)
- deg q(x) = 0
Answer:
Question 9:
Give examples of polynomials p(x), g(x), q(x)
and r(x), which satisfy the division algorithm
and
- deg p(x) = deg q(x)
- deg q(x) = deg r(x)
- deg q(x) = 0
Answer:
Question 10:
Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, –7, –14 respectively.
Answer:
Question 11:
Answer:
Question 12:
Answer:
Question 13:
Answer:
Question 14:
If one of the zeroes of the quadratic polynomial (k – 1)x2 + kx + 1 is –3, then the value of k is:
Answer:
(a)
Question 15:
A quadratic polynomial, whose zeroes are –3 and 4, is:
- x2 – x + 12
- x2 + x + 12
- 2x2 + 2x – 24
Answer:
(iv)
Question 16:
If the zeroes of the quadratic polynomial x2 + (a + 1) x + b are 2 and –3, then:
- a = –7, b = –1
- a = 5, b = –1
- a = 2, b = –6
- a = 0, b = –6
Answer:
(iv) a = 0, b = –6
Question 17:
The number of polynomials having zeroes as
–2 and 5 is
- 1
- 2
- 3
- more than 3
Answer:
(iv) more than 3
Question 18:
Given that one of the zeroes of the cubic polynomial ax3 + bx2 + cx + d is zero, the product of the other two zeroes is:
- 0
Answer:
(ii)
Question 19:
If one of the zeroes of the cubic polynomial x3 + ax2 + bx + c is –1, then the product of the other two zeroes is:
- b – a + 1
- b – a – 1
- a – b + 1
- a – b – 1
Answer:
(i) b – a + 1
Question 20:
The zeroes of the quadratic polynomial x2 + 99x + 127 are:
- both positive
- both negative
- one positive and one negative
- both equal
Answer:
(ii) both negative
Question 21:
The zeroes of the quadratic polynomial x2 + kx + k, k 0;
- cannot both be positive
- cannot both be negative
- are always unequal
- are always equal
Answer:
(i) cannot both be positive
Question 22:
If the zeroes of the quadratic polynomial ax2 + bx + c, c 0 are equal, then:
- c and a have opposite signs
- c and b have opposite signs
- c and a have the same sign
- c and b have the same sign
Answer:
(iii) c and a have the same sign
Question 23:
If one of the zeroes of a quadratic polynomial of the form x2 + ax + b is the negative of the other, then it:
- has no linear term and the constant term is negative
- has no linear term and the constant term is positive
- can have a linear term but the constant term is negative
- can have a linear term but the constant term is positive
Answer:
(i) has no linear term and the constant term is negative
Question 24:
Can x2 – 1 be the quotient on division of x6 + 2x3 + x – 1 by a polynomial in x of degree 5?
Answer:
Quotient on division of x6 + 2x3 + x – 1 by a
polynomial of degree 5 cannot be x2 – 1, because
if we multiply any polynomial of degree
5 with x2 – 1, it always becomes a polynomial
of degree 7.